Магнитный поток и потокосцепление
⇐ ПредыдущаяСтр 2 из 10Следующая ⇒
Магнитным потоком (или потоком вектора магнитной индукции через данную поверхность Sм
) называют произведение магнитной индукции
В
на площадь поверхности
Sм
поля:
| Ф = ВSм. | (6.2) |
Единица магнитного потока: [Ф
] = [
B
]
×
[
S
] = Tл
×
м2 = Вб (вебер).
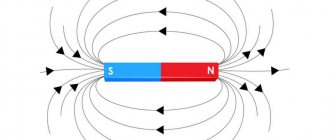
Согласно закону Гаусса для магнитного поля полный магнитный поток через замкнутую поверхность равен нулю, т. е.
.
В ряде случаев, например, при протекании тока в катушке, магнитный поток несколько раз сцепляется с витками катушки. В первом приближении можно считать, что все линии магнитной индукции сцепляются со всеми витками w
катушки. Тогда
потокосцепление катушки связывается с потоком Ф
простым соотношением:
Y
=
wФ
.
Напряжённость магнитного поля
Напряжённость магнитного поля —векторная величина, равная геометрической разности магнитной индукции , делённой на магнитную постоянную, и намагниченности вещества, т. е. Физический смысл вектора определяется законом Био-Савара: элемент тока создаёт в точке, находящейся на расстоянии от элемента тока (рис. 6.2), магнитное поле с напряжённостью
.
Единица напряжённости магнитного поля
(ампер на метр).
Зависимость от принято записывать в виде
| (6.3) |
где m
0 = 4
p×
10-7 Гн/м
—
магнитная постоянная
, магнитная проницаемость пустоты; ma = m
0
m
[Гн/м]
—абсолютная магнитная проницаемость среды (вещества); m = ma
/
m
0 — безразмерная
относительная магнитная проницаемость вещества, показывающая, во сколько раз магнитная проницаемость среды (вещества) больше (меньше) магнитной проницаемости пустоты.
В зависимости от значения m
различают:
диамагнетики с магнитной проницаемостью m <
1 (например, серебро, медь висмут; они незначительно ослабляют магнитное поле),
парамагнетики с m >
1 (например, платина, алюминий, воздух; магнитное поле в них лишь незначительно возрастает) и ферромагнетики с магнитной проницаемостью
m >>
1 (
m »
500…5000).
Намагниченность ферромагнетиков
К ферромагнитным материалам (сокращённо ферромагнетикам) относят сплавы на основе железа, никеля, кобальта и других редкоземельных элементов, их соединения; сплавы и соединения марганца, хрома, а также пластические и другие композиции с включением порошков ферромагнитных металлов (ферриты).
Свойства ферромагнитных материалов определяются значением абсолютной магнитной проницаемости ma
= /, где
ma
=
m
0
m
, а
m
— относительная магнитная проницаемость материала. Наиболее распространённые ферромагнетики – это сплавы на основе железа с добавками
Ni
,
Co
, или на основе кобальта (
Co
) с крупнозернистой структурой (с зернами-доменами размером 10-3 нм и объёмом 10-9…10-10 нм3) и с относительной магнитной проницаемостью
m
=
ma
/
m
0 = 500…5000 и более.
При отсутствии магнитного поля самопроизвольная намагниченность доменов ориентирована хаотически и результирующее магнитное поле, образованное намагниченностью этих доменов, слабое (В »
0). Под действием внешнего магнитного поля наблюдается принудительная ориентация намагниченности доменов по направлению внешнего магнитного поля и усиление результирующего магнитного потока.
Можно предположить, что при каком-то большом внешнем поле () получим одинаковую ориентацию намагниченности всех доменов (или большинства из них), и дальнейшего усиления внешнего магнитного потока Ф
и индукции
В = Ф/S
не будет. Это явление называют
насыщением ферромагнитного материала.
Кривые намагничивания
Зависимость магнитной индукции В
от напряжённости
Н
магнитного поля, т. е.
В = f
(
Н
), нелинейная (рис. 6.3) и не имеет аналитического выражения.
Для оценки свойств ферромагнетиков строят кривые намагничивания В
=
f
(
Н
), приводимые в справочниках. С их помощью можно для каждого значения напряжённости поля
Н
определить значение магнитной проницаемости
ma
, которая при возрастании напряжённости поля сначала увеличивается, затем уменьшается.
Петля гистерезиса
При протекании переменного тока в катушке с ферромагнитным сердечником происходит (в течение каждого периода тока) перемагничивание сердечника, которое на графике выглядит в виде петли — петли гистерезиса (рис. 6.4, а). Если первоначально ненамагниченный ферромагнетик намагнитить до насыщения (кривая 1), а затем уменьшить и потом снова увеличивать напряженность магнитного поля Н (ток в катушке), то изменение индукции В не будет следовать начальной кривой: каждому значению напряжённости соответствуют два значения магнитной индукции в зависимости от того, увеличивается или уменьшается напряженность поля.
Величину магнитной индукции ±Br, сохраняющуюся при Н = 0, называютостаточной индукцией; напряжённость магнитного поля ±Hc, при которой индукция обращается в нуль, называюткоэрцитивной силой.
На рис. 6.4 обозначено: ±Hmax и ±Bmax — максимальные напряжённость и индукция магнитного поля в ферромагнетике; 2 — основная кривая намагничивания ферромагнетика, проведенная через вершины семейства гистерезисных кривых (рис. 6.4, б), каждая из которых соответствует определённому значению Hmax. Приводимые в справочниках зависимости В(Н) – это основные кривые намагничивания. Они незначительно отличаются от кривых первоначального намагничивания.
⇐ Предыдущая2Следующая ⇒
Рекомендуемые страницы:
Электромагнитная индукция. Потокосцепление и индуктивность катушки (определение, формулы).
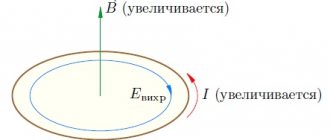
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. ПОТОКОСЦЕПЛЕНИЕ — полный магнитный поток, пронизывающий электрический контур. Напр., потокосцепление многовитковой катушки индуктивности равно сумме потоков через все ее витки. Единица измерения — Вб.
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Как следствие, при протекании через катушку переменного электрического тока, наблюдается её значительная инерционность.
Явление электромагнитной индукции. Закон электромагнитной индукции. Величина ЭДС индукции. Правило определения индукционного тока и ЭДС.
Если в соленоид, который замкнут на гальванометр, вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания мы видим отклонение стрелки гальванометра (возникает индукционный ток); при этом отклонения стрелки при вдвигании и выдвигании магнита имеют противоположные направления. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При смене в опыте полюсов магнита направление отклонения стрелки также изменится. Для получения индукционного тока можно оставлять магнит неподвижным, тогда нужно относительно магнита перемещать соленоид.
Закон Фарадея можно сформулировать еще таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
Электромагнитная индукция. Закон (правило) Ленца для электромагнитной индукции.
Индукция электромагнитная,возникновение электродвижущей силы (эдс индукции) в проводящем контуре, находящемся в переменном магнитном поле или движущемся в постоянном магнитном поле. Электрический ток, вызванный этой эдс, называется индукционным током. Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока.
Самоиндукция. Индуктивность. Энергия магнитного поля.
Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре[1] при изменении тока, протекающего по контуру.
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур
Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. ПОТОКОСЦЕПЛЕНИЕ — полный магнитный поток, пронизывающий электрический контур. Напр., потокосцепление многовитковой катушки индуктивности равно сумме потоков через все ее витки. Единица измерения — Вб.
Катушка индуктивности — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Как следствие, при протекании через катушку переменного электрического тока, наблюдается её значительная инерционность.
Явление электромагнитной индукции. Закон электромагнитной индукции. Величина ЭДС индукции. Правило определения индукционного тока и ЭДС.
Если в соленоид, который замкнут на гальванометр, вдвигать или выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания мы видим отклонение стрелки гальванометра (возникает индукционный ток); при этом отклонения стрелки при вдвигании и выдвигании магнита имеют противоположные направления. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки. При смене в опыте полюсов магнита направление отклонения стрелки также изменится. Для получения индукционного тока можно оставлять магнит неподвижным, тогда нужно относительно магнита перемещать соленоид.
Закон Фарадея можно сформулировать еще таким образом: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
Электромагнитная индукция. Закон (правило) Ленца для электромагнитной индукции.
Индукция электромагнитная,возникновение электродвижущей силы (эдс индукции) в проводящем контуре, находящемся в переменном магнитном поле или движущемся в постоянном магнитном поле. Электрический ток, вызванный этой эдс, называется индукционным током. Закон Джоуля — Ленца — физический закон, дающий количественную оценку теплового действия электрического тока.
Самоиндукция. Индуктивность. Энергия магнитного поля.
Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре[1] при изменении тока, протекающего по контуру.
При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур
Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I.
Определение
Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N
и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как \Psi = N\Phi_1, где \Phi_1 — магнитный поток одного витка [ ].
В идеальном соленоиде все магнитные силовые линии проходят через каждый виток (т.е. не пересекают боковую поверхность соленоида), и, следовательно, магнитный поток каждого витка одинаков. Однако на практике магнитные потоки в витках катушки отличаются и величина потокосцепления определяется по формуле:
\Psi = \sum^{N}_{i=1} {\Phi_i},
где: N — количество витков; i — номер витка, с которым сцеплен поток \Phi_i.
В случае, если катушка имеет ферромагнитный сердечник, потокосцепление можно определить по формуле:
\Psi = N\Phi_C,
где \Phi_C — магнитный поток через магнитопровод (сердечник) катушки.
Величина потокосцепления, помимо магнитного потока, имеет связь с током I
в индуктивности, определяющуюся выражением:
\Psi = IL,
где L — индуктивность катушки [ ].
Эта формула выражает принцип непрерывности во времени потокосцепления катушки индуктивности.