Магнитный поток
Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.
Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.
Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
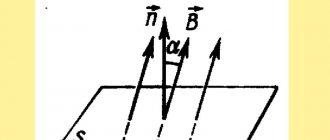
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению:
- модуля вектора магнитной индукции B,
- площади поверхности S, которую пронизывает поток,
- и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).
| Магнитный поток Ф — магнитный поток [Вб] B — магнитная индукция [Тл] S — площадь пронизываемой поверхности [м2] n — вектор нормали (перпендикуляр к поверхности) [-] |
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
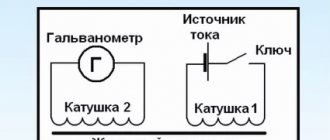
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
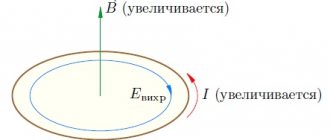
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока различается при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
ИЗУЧЕНИЕ ЯВЛЕНИЯ ВЗАИМНОЙ ИНДУКЦИИ
Приборы:
генератор Г3 – 112/1, осциллограф С1 – 117, кассета с двумя катушками ФПЭ – 05/06.
Цель работы:
изучение явления взаимной индукции.
Введение
1. Явление электромагнитной индукции.
В 1831г. английским учёным Фарадеем было открыто явление электромагнитной индукции: в замкнутом проводящем контуре возникает индукционный ток при изменении числа магнитных линий, пронизывающих площадь, ограниченную контуром.
ЭДС индукции, возникающая в контуре, подчиняется закону Фарадея:
т.е. зависит только от скорости изменения потока магнитной индукции Ф, пронизывающего контур. По правилу Ленца индукционный ток имеет такое направление, что его магнитное поле препятствует вызвавшему его изменению магнитного потока.
2. Явление самоиндукции.
Ток в замкнутом контуре создаёт вокруг себя магнитное поле, и этот контур пронизывает собственный магнитный поток Ф, пропорциональный току в контуре:
Ф = Li
L — коэффициент самоиндукции или индуктивность контура, Гн.
При изменении тока i будет меняется и магнитный поток, связанный с контуром, тогда в контуре возникает ЭДС самоиндукции:
Если L = const,
то = — L
Явление возникновения ЭДС индукции в том самом контуре, по которому течет переменный ток, называется самоиндукцией.
3. Взаимная индукция.
Рассмотрим два контура. Контур 1 присоединен к источнику тока Е, с помощью реостата R можно менять ток i1 в этом контуре.
Ток i1 создаёт вокруг себя магнитное поле, линии индукции которого пронизывают контур 2, замкнутый на гальванометр.
Ф21 – магнитный поток, пронизывающий контур 2; Ф21 ~ i1, Ф21 = М21i1. M21 называется коэффициентом взаимной индукции или взаимной индуктивностью двух контуров. Взаимная индуктивность двух контуров численно равна магнитному потоку во втором контуре, когда ток в первом контуре равен единице (1 А).
Единица взаимной индуктивности в системе СИ также носит название Генри (Гн)
М = 1 Гн, 1 Гн = ВС/А
Если пропустить ток i2 через второй контур, то теперь уже первый контур будет пронизывать магнитный поток Ф12, пропорциональный току i2.
Ф12 = М122. Можно показать, что М21 = М12 = М.
Взаимная индуктивность двух контуров зависит от формы, размеров и взаимного расположения контуров, а также от магнитной проницаемости окружающей контуры среды.
Если ток i1 будет меняться, то будет изменяться и магнитный поток Ф21, тогда по закону электромагнитной индукции возникает ЭДС взаимной индукции во втором контуре:
(если контуры неподвижны и недеформируемые, М = const). Я вление возникновения ЭДС в одном из контуров при изменении силы тока в другом называется взаимной индукцией.
Отсюда – взаимная индуктивность двух контуров численно равна ЭДС индукции, возникающей в одном из этих контуров, тогда ток в другом контуре убывает на единицу за единицу времени.
Пример 1
Ф21 = 2Ф, где Ф – магнитный поток черев виток 1; гальванометр покажет отброс при изменении тока в цепи первой катушки.
Пример 2
Витки второй катушки охватывают первую в противоположных направлениях:
Ф21 = Ф – Ф = 0
Во второй катушке ЭДС индукции не возникает при изменении тока в цепи, что используется в бифиллярной намотке проводов, когда необходимо избежать возникновения паразитных индукционных токов.
На практике явление взаимной индукции применяется в трансформаторах.
Две катушки, намотанные на общий стальной сердечник, образуют трансформатор переменного тока. Он был изобретён Яблочковым П.Н. в 1876 г.
Трансформатор предназначен для преобразования величин переменных напряжений и токов.
К первичной обмотке с числом витков ω1 подключена переменная внешняя ЭДС Е1.
Запишем для нее закон Ома:
где i1 – ток в первичной обмотке
r1 – ее сопротивления
1 – внешняя ЭДС
— d (ω1Ф)/dt – ЭДС самоиндукции в первичной цепи
Ф – магнитный поток через виток 1.
Практически падение напряжения на сопротивление r1 мало, поэтому
Возникающая во вторичной обмотке ЭДС
Получаем
Отношение числа витков во вторичной обмотке к числу витков в первичной обмотке называется коэффициентом трансформации.
Если ω2/ω1>1 – трансформатор повышающий, Е2>Е1.
Если ω2/ω1<1 – трансформатор понижающий.
Трансформаторы широко применяются в электротехнике и радиотехнике.
Самоиндукция
Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.
| Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток [Вб] L — индуктивность контура [Гн] I — сила тока в контуре [А] |
Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.
Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.
Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.
Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:
- первая лампа загорится практически сразу,
- вторая лампа загорится с заметным запаздыванием.
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.
| ЭДС самоиндукции ξis — ЭДС самоиндукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность [Гн] |
Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.
Явление самоиндукции и взаимоиндукции. Индуктивность
Полный магнитный поток через плоскости всех витков катушки, созданный током в этой же катушке, называется потокосцеплением самоиндукции Ym. Возникновение ЭДС при всяком изменении потокосцепления самоиндукции в катушке называется явлением самоиндукции.
Потокосцепление самоиндукции катушки прямо пропорционально силе тока в ней
Ym= Fm×N = L×I, (3.4)
где N — число витков катушки, L — индуктивность катушки.
Индуктивностью называется физическая величина, численно равная потокосцеплению самоиндукции контура при силе тока в нем, равном 1 А.
Индуктивность зависит от размеров и формы контура, а также от магнитных свойств окружающей среды.
Единицей измерения индуктивности (СИ) является 1 Генри (Гн).
Индуктивность длинного соленоида (длина соленоида l
много больше его диаметра D) (рис. 3.1) определяется по формуле:
, (3.5)
где N – общее число витков соленоида, -площадь поперечного сечения соленоида, m -относительная магнитная проницаемость сердечника соленоида.
Если сердечник ферромагнитный, то m зависит от напряжённости Н магнитного поля, а, следовательно, от силы тока в соленоиде.
В случае, когда витки соленоида плотно прилегают друг к другу, длину соленоида можно найти через диаметр проволоки d и общее число витковN:
l
=d∙N. (3.6)
Число витков, приходящихся на единицу длины соленоида:
. (3.7)
Длину провода, из которого навит соленоид, можно найти через длину одного витка и общее число витков:
l
пр=pD×N. (3.8)
Величина ЭДС самоиндукции определяется скоростью изменения потокосцепления самоиндукции и в общем случае равна:
. (3.9)
В частном случае, при L=const:
. (3.10)
Явление самоиндукции в электрических цепях аналогично инерции в механике. При замыкании и размыкании электрической цепи возникающие токи самоиндукции (экстратоки), согласно правилу Ленца, направлены так, чтобы препятствовать изменению тока в цепи. Это приводит к тому, что установление и исчезновение кстратоки, ой тока в цепи происходит не мгновенно, а постепенно.
Закон изменения тока при замыкании цепи можно представить как:
, (3.11)
гдеR- сопротивление цепи, Iо- установившееся значение силы тока в цепи.
При отключении источника тока закон изменения тока выглядит так:
. (3.12)
Если имеются два контура с токами, то может наблюдаться явление взаимной ЭМИ. Каждый из контуров создает своё магнитное поле. Часть силовых линий поля, создаваемого первым контуром, будет пересекать второй и наоборот.
Потокосцепление второго контура, созданное током I1 первого контура, называется потокосцеплением взаимоиндукции и пропорционально силе тока I1:
Y21=L21×I1. (3.13) Аналогично
Y12=L12×I2.
При изменении в первом контуре тока I1 во втором возникает ЭДС индукции
. (3.14)
При изменении во втором контуре тока I2 в первом возникает ЭДС индукции
.
Контуры 1 и 2 называются связанными, а явление возникновения ЭДС индукции в одном из контуров при изменении силы тока в другом называется явлением взаимной ЭМИ. Коэффициенты пропорциональности L12=L21 называются взаимной индуктивностью контуров. Она зависит от размеров и формы контуров, их взаимного расположения, а также от магнитных свойств окружающей среды. Взаимная индуктивность численно равна потокосцеплению взаимоиндукции одного из контуров при единичной силе тока в другом.
Полный магнитный поток через плоскости всех витков катушки, созданный током в этой же катушке, называется потокосцеплением самоиндукции Ym. Возникновение ЭДС при всяком изменении потокосцепления самоиндукции в катушке называется явлением самоиндукции.
Потокосцепление самоиндукции катушки прямо пропорционально силе тока в ней
Ym= Fm×N = L×I, (3.4)
где N — число витков катушки, L — индуктивность катушки.
Индуктивностью называется физическая величина, численно равная потокосцеплению самоиндукции контура при силе тока в нем, равном 1 А.
Индуктивность зависит от размеров и формы контура, а также от магнитных свойств окружающей среды.
Единицей измерения индуктивности (СИ) является 1 Генри (Гн).
Индуктивность длинного соленоида (длина соленоида l
много больше его диаметра D) (рис. 3.1) определяется по формуле:
, (3.5)
где N – общее число витков соленоида, -площадь поперечного сечения соленоида, m -относительная магнитная проницаемость сердечника соленоида.
Если сердечник ферромагнитный, то m зависит от напряжённости Н магнитного поля, а, следовательно, от силы тока в соленоиде.
В случае, когда витки соленоида плотно прилегают друг к другу, длину соленоида можно найти через диаметр проволоки d и общее число витковN:
l
=d∙N. (3.6)
Число витков, приходящихся на единицу длины соленоида:
. (3.7)
Длину провода, из которого навит соленоид, можно найти через длину одного витка и общее число витков:
l
пр=pD×N. (3.8)
Величина ЭДС самоиндукции определяется скоростью изменения потокосцепления самоиндукции и в общем случае равна:
. (3.9)
В частном случае, при L=const:
. (3.10)
Явление самоиндукции в электрических цепях аналогично инерции в механике. При замыкании и размыкании электрической цепи возникающие токи самоиндукции (экстратоки), согласно правилу Ленца, направлены так, чтобы препятствовать изменению тока в цепи. Это приводит к тому, что установление и исчезновение кстратоки, ой тока в цепи происходит не мгновенно, а постепенно.
Закон изменения тока при замыкании цепи можно представить как:
, (3.11)
гдеR- сопротивление цепи, Iо- установившееся значение силы тока в цепи.
При отключении источника тока закон изменения тока выглядит так:
. (3.12)
Если имеются два контура с токами, то может наблюдаться явление взаимной ЭМИ. Каждый из контуров создает своё магнитное поле. Часть силовых линий поля, создаваемого первым контуром, будет пересекать второй и наоборот.
Потокосцепление второго контура, созданное током I1 первого контура, называется потокосцеплением взаимоиндукции и пропорционально силе тока I1:
Y21=L21×I1. (3.13) Аналогично
Y12=L12×I2.
При изменении в первом контуре тока I1 во втором возникает ЭДС индукции
. (3.14)
При изменении во втором контуре тока I2 в первом возникает ЭДС индукции
.
Контуры 1 и 2 называются связанными, а явление возникновения ЭДС индукции в одном из контуров при изменении силы тока в другом называется явлением взаимной ЭМИ. Коэффициенты пропорциональности L12=L21 называются взаимной индуктивностью контуров. Она зависит от размеров и формы контуров, их взаимного расположения, а также от магнитных свойств окружающей среды. Взаимная индуктивность численно равна потокосцеплению взаимоиндукции одного из контуров при единичной силе тока в другом.
Индуктивность
Индуктивность — это способность катушки, контура или проводника с током накапливать магнитное поле. Она характеризует способность проводника сопротивляться электрическому току. Проще всего это делать с помощью катушки, потому что катушка состоит из витков, которые представляют собой контуры. Вспомните про магнитный поток и обруч под дождем — в контуре создается магнитный поток. Где поток, там и электромагнитная индукция.
Индуктивность контура зависит от его формы и размеров, от магнитных свойств окружающей среды и не зависит от силы тока в контуре.
Можно ли увеличивать индуктивность катушки?
Конечно! Можно увеличить число витков, например. Или поместить в центр катушки железный сердечник.
Как работает катушка
Вокруг каждого проводника, по которому протекает ток, образуется магнитное поле. Если поместить проводник в переменное поле — в нем возникнет ток.
Магнитные поля каждого витка катушки складываются. Поэтому вокруг катушки, по которой протекает ток, возникает сильное магнитное поле. При изменении силы тока в катушке будет изменяться и магнитный поток вокруг нее.
Задачка раз
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн. Определите модуль ЭДС самоиндукции в интервале времени от 15 до 20 с. Ответ выразите в мкВ.
Решение
За время от 15 до 20 с сила тока изменилась от 20 до 0 мА. Модуль ЭДС самоиндукции равен:
Ответ: модуль ЭДС самоиндукции с 15 до 20 секунд равен 4 мкВ.
§24. Взаимоиндукция
Взаимоиндукцией называется явление индуцирования э. д. с. в проводнике или катушке при изменении магнитного потока, создаваемого другим проводником (катушкой). Индуцируемая таким образом э. д. с. ем носит название э. д. с. взаимоиндукции. Примером является индуцирование э. д. с. ем в проводнике ВГ (см. рис. 54) при изменении тока i1 в проводнике АБ, а также индуцирование э. д. с. е2 в катушке 2 (см. рис. 55, а) при изменении тока в катушке 1.
Если два замкнутых контура или две катушки 1 и 2 (рис. 66) сцеплены с общим магнитным потоком Ф12, то такие контуры и катушки называют индуктивно или магнитносвязанными. Для оценки степени их связи введено понятие взаимоиндуктивности М. Взаимоиндуктивность, так же как и индуктивность L, измеряется в генри (Гн).
Если известна взаимоиндуктивность М, то э. д. с. взаимоиндукции ем, индуцированная в каком-либо контуре или катушке, при изменении тока i в другом контуре или катушке может быть получена из формулы (51) для индуцированной э. д. с. При этом
ем = – M ?i / ?t (55)
Рис. 66. Две индуктивно связанные катушки
Следовательно, э. д. с. взаимоиндукции так же как и э. д. с. само индукции, пропорциональна скорости ?i/?t изменения тока, создающего магнитное поле. Кроме того, она зависит от числа витков обеих катушек ?1 и ?2 и от магнитного сопротивления связывающего их магнитопровода (т. е. от его длины l, поперечного сечения s и магнитной проницаемости). Направление э. д. с. взаимоиндукции определяется по правилу Ленца: она всегда направлена так, что стремится препятствовать изменению создающего ее тока.
Взаимоиндукция дает возможность связывать посредством магнитного поля различные электрические цепи. Явление взаимоиндукции широко используются в трансформаторах, радиотехнических устройствах и устройствах автоматики. Однако в некоторых случаях возникновение э. д. с. взаимоиндукции является нежелательным. Например, э. д. с. взаимоиндукции, индуцированные в линиях связи (телефонных и телеграфных проводах), проложенных вдоль высоковольтных линий электропередачи или вдоль контактной сети электрофицированных железных дорог переменного тока, создают помехи при передаче телефонных или телеграфных сигналов. Поэтому линии связи стремятся располагать перпендикулярно проводам линий электропередачи или выполнять их в виде кабельных линий, защищенных металлическими экранами.