Электромагнитная индукция определение и описание явления.

Средняя оценка: 4.5

Всего получено оценок: 60.

4.5

Средняя оценка: 4.5

Всего получено оценок: 60.

ЭДС индукции возникает в контуре при изменении магнитного потока через него. Более редким случаем магнитной индукции является движение уединенного проводника в магнитном поле. Кратко рассмотрим ЭДС индукции в движущихся проводниках.

Механизм индукции в движущемся проводнике

Из курса физики в 11 классе известно, что электрический ток — это движение носителей заряда. Если магнитный поток через контур изменяется, то в контуре возникает вихревое электрическое поле, благодаря которому и движутся носители и возникает электрический ток. Однако это не единственный способ создать в проводнике движение зарядов.

Вторым способом создания в проводнике движущихся зарядов является использование силы Лоренца. Если эта сила начнет действовать на носители заряда в проводнике, то в нем возникнет ЭДС и электрический ток.

Рис. 1. Сила Лоренца.

Сила Лоренца действует только на движущиеся заряды. Следовательно, если проводник, в котором есть носители заряда, начнет двигаться в магнитном поле, то на заряды начнет действовать сила, и они придут в движение — в проводнике возникнет ЭДС.

Заметим, что ЭДС, возникающая в этом случае в проводнике, имеет иную причину, по сравнению с изменением магнитного потока через контур. Если при изменении потока причиной возникновения ЭДС является вихревое электрическое поле, то в движущемся проводнике причиной ЭДС является сила Лоренца.

Обозначение и единицы измерения

В системе единиц СИ индуктивность измеряется в генри, сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 10 9 см) . Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.

Символ , используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz)

. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry) [8] . Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.

Электрический ток, который течет в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, согласно закону Био-Савара-Лапласа, пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому прямо пропорционален току I в контуре: где коэффициент пропорциональности L называетсяиндуктивностью контура. При изменении в контуре силы тока будет также изменяться и сцепленный с ним магнитный поток; значит, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называетсясамоиндукцией. Из выражения задается единица индуктивности генри (Гн): 1 Гн — индуктивность контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В

Вычислим индуктивность бесконечно длинного соленоида. Полный магнитный поток сквозь соленоид (потокосцепление) равен μμ(N 2 I/l)S . Подставив в найдем т. е. индуктивность соленоида зависит от длиныl солениода, числа его витков N, его , площади S и магнитной проницаемости μ вещества, из которого изготовлен сердечник соленоида. Доказано, что индуктивность контура зависит в общем случае только от геометрической формы контура, его размеров и магнитной проницаемости среды, в которой он расположен, и можно провести аналог индуктивности контура с электрической емкостью уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды. Найдем, применяя к явлению самоиндукции закон Фарадея, что э.д.с. самоиндукции равна Если контур не претерпевает деформаций и магнитная проницаемость среды остается неизменной (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L = const и (3) где знак минус, определяемый правилом Ленца, говорит о том, чтоналичие индуктивности в контуре приводит к замедлению изменения тока в нем. Если ток со временем увеличивается, то (dI/dt 0 т. е. ток самоиндукции направлен навстречу току, обусловленному внешним источником, и замедляет его увеличение. Если ток со временем уменьшается, то (dI/dt>0) и ξs >1), обладающей боль­шой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникнове­ние значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.

Будет интересно➡ Кабель ВВГНГ: конструкция, маркировка, основные характеристики

Явление взаимной индукции. Трансформатор.

Рассмотрим два неподвижных контура, которые расположены достаточно близко друг от друга. Если в контуре 1 протекает ток , то магнитный поток, который создавается этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), прямо пропорционален I1. Обозначим через Ф21 часть потока,пронизывающая контур 2. Тогда где L21 — коэффициент пропорциональности.

Если ток I1 меняет свое значение, то в контуре 2 индуцируется э.д.с. ξi2 , которая по закону Фарадея будет равна и противоположна по знаку скорости изменения магнитного потока Ф21, который создается током в первом контуре и пронизыващет второй: Аналогичным образом, при протекании в контуре 2 тока I2 магнитный поток пронизывает первый контур. Если Ф12 — часть этого потока, который пронизывает контур 1, то Если ток I2 меняет свое значение, то в контуре 1 индуцируется э.д.с. ξi1 , которая равна и противоположна по знаку скорости изменения магнитного потока Ф12, который создается током во втором контуре и пронизывает первый: Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией. Коэффициенты пропорциональности L21 и L12 называются взаимной индуктивностью контуров. Расчеты, которые подтверждены опытом, показывают, что L21 и L12 равны друг другу, т. е. Коэффициенты пропорциональности L12 и L21 зависят от размеров, геометрической формы, взаимного расположения контуров и от магнитной проницаемости среды, окружающей контуры. Единица взаимной индуктивности та же, что и для индуктивности, — генри (Гн). Найдем взаимную индуктивность двух катушек, которые намотаны на общий тороидальный сердечник. Этот случай имеет большое практическое значение. Магнитная индукция поля, которое создавается первой катушкой с числом витков N1, током I1 и магнитной проницаемостью μ сердечника, B = μμ(N1I1/l) где l — длина сердечника по средней линии. Магнитный поток сквозь один виток второй катушки Ф2 = BS = μμ(N1I1/l)S

Значит, полный магнитный поток (потокосцепление) сквозь вторичную обмотку, которая содержит N2 витков, Поток Ψ создается током I1, поэтому, используя, найдем Если рассчитать магнитный поток, который создавается катушкой 2 сквозь катушку 1, то для L12 получим выражение в соответствии с формулой. Значит, взаимная индуктивность двух катушек, которые намотаны на общий тороидальный сердечник, Трансформа́тор (от лат.transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока

ЭДС индукции в движущемся проводнике

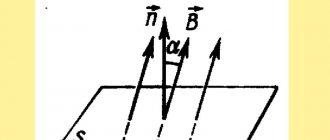
Вычислим ЭДС индукции в проводнике длиной $l$, который движется с постоянной скоростью $v$ так, что вектор магнитной индукции $\overrightarrow B$ однородного поля перпендикулярен проводнику и направлен под углом $\alpha$ к скорости движения проводника.

По формуле силы Лоренца ее величина равна:

$$F=|q|Bvsin\alpha$$

Компонента этой силы, направленная вдоль проводника, совершает положительную работу, которая на пути $l$ равна:

$$А=Fl=|q|Bvlsin\alpha$$

Заметим, что вторая компонента силы Лоренца совершает равную по модулю отрицательную работу. Поэтому суммарная работа силы Лоренца равна нулю.

ЭДС по определению равна отношению работы, совершенной полем по переносу зарядом, к величине этого заряда. Следовательно:

$$\mathscr{E} = {A\over q}=Bvlsin\alpha$$

Движение контура в магнитном поле

Формулу ЭДС индукции в движущихся проводниках можно применить к прямоугольному контуру, разбив его на четыре элементарных проводника (по числу сторон). В этом случае ЭДС, возникающие в противоположных сторонах контура, будут направлены в противоположные стороны. В результате суммарная ЭДС в контуре будет равна нулю. Следовательно, при движении контура в однородном магнитном поле ток в нем возникнуть не может.

Этот же вывод можно сделать и из закона электромагнитной индукции. Если контур движется в однородном магнитном поле, то магнитный поток, пронизывающий его, не изменяется, следовательно, ЭДС индукции, возникающая в нём, равна нулю.

Единственная возможность создать ЭДС в контуре, движущемся в однородном магнитном поле, это совершить его поворот таким образом, чтобы ЭДС возникала за счет изменения компоненты $sin\alpha$. Действительно, такой поворот будет изменять магнитный поток через контур, а значит, в нём будет возникать ЭДС индукции.

Влияние числа витков и способа намотки

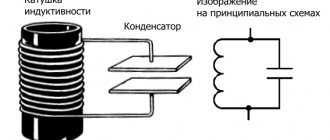
Катушка индуктивности – это спираль, созданная из проводящего материала. Рабочие параметры изделий будут зависеть от особенностей конструкции. Индуктивность увеличивают:

• большим количеством витков на единицу длины;
• укрупнением поперечного сечения;
• установкой в центральной части сердечника с ферромагнитными характеристиками.

От чего зависит индуктивность катушки, примеры типовых решений

Индуктивность одновиткового контура и индуктивность катушки

Для расчета элементарной конструкции подойдет преобразованная первая формула:

Ф = L * I.

Если рассматривается катушка, это выражение трансформируют в суммарное выражение магнитных потоков (Ψ), образованных отдельными витками:

Ψ = n * Ф.

Аналогичным образом:

Ln = L1 * n.

В действительности для точных расчетов учитывают различия силовых линий в центральной части и на краях конструкции. Для коррекции применяют более сложные выражения.

Индуктивность соленоида

Достаточно длинная электрическая катушка формирует внутри параллельные силовые линии. Для создания равномерного распределения энергии необходимо применять проводник с толщиной намного меньше, по сравнению с диаметром поперечного сечения. Разумеется, необходимо установить одинаковое расстояние между отдельными витками.

Такую конструкцию называют соленоидом. Плотность магнитного потока (B) в центральной рабочей части будет зависеть прямо пропорционально от длины (l) и следующих параметров:

• количества витков (N);
• тока (i);
• плотности намотки (n – число контуров на единицу длины);
• площади поперечного сечения (S);
• объема (V = S * l).

Ниже приведены основные формулы для вычислений при отсутствии сердечника с учетом магнитной постоянной (m ≈ 1,257 *10-6 Гн/ м):

• В = m0 * N * (i/l) = m0 * n * I;
• Ψ = m0 * N2 * (I * S/l) = m0 * n2 * i *V;
• L = m0 * N2 * (S/l) = m0 * n2 * V.

Индуктивность тороидальной катушки (катушки с кольцевым сердечником)

Для вычисления индукции катушки с сердечником в представленные выше формулы добавляют корректирующий множитель «m». С учетом особой формы изделия необходимо сделать следующие изменения:

L = N2 * ((m0 * m * S)/2π * rL), либо L = N2 * ((m0 * m * h)/2π) * ln(R/r),

где:

• 2π * rL – длина рабочего элемента со средним радиусом rL;
• R (r) и h – наружный (внутренний) радиус и высота тора, соответственно.

Коэффициентом «m» учитывают относительный показатель магнитной проницаемости определенного материала к значению для нейтральной среды (вакуума). Если m намного больше единицы, допускается не учитывать искажения поля, которые создает толстый проводник.