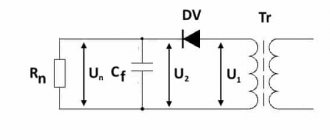
Однофазный мостовой неуправляемый выпрямитель

В схему выпрямителя (рис. 17, а) входят силовой трансформатор с одной вторичной обмоткой и выпрямительный мост из четырех диодов VD1-VD4. Принцип действия выпрямителя рассмотрим, приняв нагрузку выпрямителя чисто активной.

Выходное напряжение ud при чисто активной нагрузке имеет вид однополярных полуволн напряжения u2 (рис. 17, в). Это получается в результате поочередного отпирания диодов VD1, VD2 и VD3, VD4.

Однофазный мостовой выпрямитель

Рис. 17. Схема однофазного мостового выпрямителя (а)

и его временные диаграммы (б-ж)

Диоды VD1, VD2 открыты на интервале при полуволне напряжения u2 положительной полярности (показана на рис. 17, а без скобок), создаваемого под действием напряжения и1 (рис. 17, б, в). Открытые диоды VD1, VD2 обеспечивают связь вторичной обмотки трансформатора с нагрузкой, создавая на ней напряжение иd той же величины и полярности, что и напряжение u2 (рис. 17, в). При наличии полуволны напряжения u1 отрицательной полярности на интервале полярность напряжения u2 обратная. Под ее воздействием открыты диоды VD3, VD4, подключающие напряжение u2 к нагрузке с той же полярностью, что и на предыдущем интервале (рис. 17, а, в). Ввиду идентичности кривых ud для выпрямителей (мостового и с выводом нулевой точки трансформатора) для схемы рис. 17, а действительны соотношения (19), (20) между выпрямленным напряжением Ud и действующим значением напряжения U2 и соотношения (22)-(24), характеризующие гармонический состав и коэффициент пульсации выходного напряжения. Все параметры схемы сведены в таблицу 3. Подробный расчет приведен в [1, 2].

Поскольку ток Id = Ud/RH (рис. 17, г) распределяется поровну между парами диодов (рис. 17, д, e)

Обратное напряжение прикладывается одновременно к двум непроводящим диодам на интервале проводимости двух других диодов. При этом оно создаётся напряжением вторичной обмотки трансформатора u2. Кривая ub для диодов VD1 VD2 показана на рис. 17, ж. Максимальное обратное напряжение определяется амплитудным значением напряжения u2 (табл. 3), т. е. оно вдвое меньше, чем в схеме с выводом нулевой точки.

В рассматриваемой схеме параметры первичной обмотки I1 , U1 связаны соответственно с параметрами вторичной обмотки I2 , U2 коэффициентом трансформации n. В соответствии с этим расчетные мощности обмоток получаются одинаковыми и мощность трансформатора ST=1,23Pd (табл. 3).

Преимуществами мостовой схемы выпрямителя являются более простой трансформатор, содержащий только одну вторичную обмотку, и меньшее обратное напряжение (при данном напряжении Ud), на которое следует выбирать диоды. Указанные преимущества компенсируют недостаток схемы, заключающийся в большем числе диодов. Поэтому мостовая схема нашла преобладающее применение в выпрямителях однофазного тока небольшой и средней мощности.

62. Однофазный нулевой управляемый выпрямитель

Схема однофазного управляемого выпрямителя с нулевым выводом, выполняемая по аналогии со схемой неуправляемого выпрямителя (см. рис. 13, а), приведена на рис. 23. Ее анализ будем проводить для двух видов нагрузки — чисто активной и активно-индуктивной. Примем вначале нагрузку чисто активной (ключ К1 включен, ключ К2 выключен).

Однофазный нулевой управляемый выпрямителя

Режиму активной нагрузки соответствуют временные диаграммы, приведенные на рис. 24, а-е. Пусть на входе выпрямителя действует положительная полуволна напряжения сети u1 (рис. 24, а), чему соответствуют полярности напряжений на обмотках трансформатора, указанные на рис. 23 без скобок. На интервале тиристоры Т1, Т2 закрыты, напряжение на выходе выпрямителя ud=0 (рис. 24, в). К тиристорам Т1, Т2 прикладывается суммарное напряжение двух вторичных обмоток трансформатора u2-1+u2-2 На тиристоре Т1 действует напряжение в прямом направлении, а на тиристоре Т2 — в обратном. Если сопротивления непроводящих тиристоров при прямом и обратном напряжениях считать одинаковыми, то на интервале напряжение на тиристорах (с учетом соответствующей полярности) будет определяться величиной (u2-1—u2-2)/2 = u 2 (рис. 24, е).

В момент времени определяемый углом , от системы управления СУ выпрямителя поступает импульс на управляющий электрод тиристора Т1 (рис. 24, б). В результате отпирания тиристор Т1 подключает нагрузку Rн на напряжение u2-1=u2 вторичной обмотки трансформатора. На нагрузке на интервале формируется напряжение ud (рис. 24, в), представляющее собой участок кривой напряжения u2-1=u2. Через нагрузку и тиристор Т1 протекает ток (рис. 24, г) id = ial = ud/Rн. При переходе напряжения питания через нуль ( ) ток тиристора Т1 становится равным нулю и тиристор закрывается.

На интервале полярность напряжения питания изменяется на противоположную. На этом интервале оба тиристора выпрямителя закрыты. К тиристору Т1 (рис. 24, е) прикладывается обратное напряжение, а к тиристору Т2 — прямое напряжение, равное Т2.

Временные диаграммы

Временные диаграммы, иллюстрирующие принцип действия однофазного управляемого выпрямителя с нулевым выводом при чисто активной нагрузке.

По окончании указанного интервала подается отпирающий импульс на тиристор Т2. Отпирание этого тиристора вызывает приложение к нагрузке напряжения ud=u2-2=u2 (рис. 24, в) той же формы, что и на интервале проводимости тиристора Т1. Через нагрузку и тиристор протекает ток id = ia2 = ud/Rн (рис. 24, д). На интервале проводимости тиристора Т2 напряжения двух вторичных обмоток трансформатора подключаются к тиристору Т2, вследствие чего с момента отпирания тиристора Т2 на тиристоре Т1 действует обратное напряжение, равное 2u2 (рис. 6.2, е). Максимальному обратному напряжению соответствует значение Ubmax=2 U2, где U2 — действующее значение вторичного напряжения трансформатора. В последующем процессы в схеме следуют аналогично рассмотренным. Токи вторичных обмоток трансформатора определяются токами тиристоров Т1, Т2 (рис. 24, г, д). Первичный ток i1 (рис. 24, а) связан с вторичными токами коэффициентом трансформации трансформатора и имеет паузы на интервалах . Его первая гармоника имеет фазовый сдвиг в сторону отставания относительно напряжения питания.

Особенностью управляемого выпрямителя является его способность регулировать среднее значение выпрямленного напряжения Ud при изменении угла (рис. 24, в). При = 0 кривая выходного напряжения ud соответствует случаю неуправляемого выпрямителя (см. §7) и напряжение максимально. Углу управления (180 эл. град) отвечают ud = 0 и Ud = 0. Иными словами, управляемый выпрямитель при изменении угла от 0 до 180 эл. град осуществляет регулирование напряжения Ud в пределах от максимального значения, равного 0,9U2, до нуля. Вид кривых ud при различных значениях угла показан на рис. 25, а-г.

Зависимость напряжения Ud от угла называется регулировочной характеристикой управляемого выпрямителя. Она определяется из выражения для среднего значения напряжения на нагрузке. Это напряжение на интервале соответствует синусоиде вторичного напряжения (см. рис. 24, в или 25, б, в), т. е.

Результат расчета дает

где Ud0 = 0,9U2 — среднее значение напряжения на нагрузке при .

Кривые выходного напряжения однофазного выпрямителя при

чисто активной нагрузке и различных углах управления

Регулировочная характеристика

однофазного управляемого выпрямителя

63. Трехфазный нулевой управляемый выпрямитель

Особенность работы трехфазного нулевого управляемого выпрямителя заключается в задержке на угол момента отпирания очередных тиристоров относительно точек естественного отпирания имеющих координаты и т. д. (рис. 31, б).

Трехфазный нулевой управляемый выпрямитель

Схема трехфазного нулевого управляемого выпрямителя (а), его временные диаграммы (б) и регулировочная характеристика (в)

В кривой выпрямленного напряжения вырезаются участки синусоиды, вследствие чего среднее значение напряжения Ud уменьшается. Таким образом, при изменении угла осуществляется регулирование величины Ud.

Влияние изменения угла на кривую ud и среднее значение напряжения Ud показаны на рис. 31, б. Кривая ud на рис. 31, б, состоит из участков фазных напряжений вторичных обмоток трансформатора ua, ub, uc.

При изменении угла в диапазоне от 0 до 30° (рис. 31, б) переход напряжения ud с одного фазного напряжения на другое осуществляется в пределах положительной полярности участков фазных напряжений. Поэтому форма кривой напряжения ud и его среднее значение одинаковы как при активной, так и при активно-индуктивной нагрузках. Ток нагрузки непрерывен.

При >30° вид кривой ud зависит от характера нагрузки (рис. 31, б). Причина зависимости та же, что и в управляемых выпрямителях однофазного тока (см. §12). В случае активно-индуктивной нагрузки ток id продолжает протекать через тиристоры и вторичные обмотки трансформатора после изменения полярности их фазного напряжения, в связи с чем в кривой и появляются участки фазных напряжений отрицательной полярности. При эти участки продолжаются до моментов очередного отпирания тиристоров. Равенству площадей участков и условию Ud=0 соответствует угол =90°. Значение этого угла характеризует нижний предел регулирования напряжения Ud при . При активной нагрузке участки напряжения отрицательной полярности отсутствуют и в кривой ud при > 30° появляются нулевые паузы. Напряжению Ud=0 теперь будет отвечать значение угла = 150o.

Зависимость среднего значения выпрямленного напряжения от угла (регулировочная характеристика) при может быть найдена усреднением кривой ud на интервале 2 :

т. е. она определяется тем же соотношением, что и в однофазных схемах.

Участок регулировочной характеристики при активной нагрузке ( ) на интервале 150° > > 30° находят из выражения

При этом закрытие тиристора происходит в точке, соответствующей нулевому напряжению ранее, чем открытие следующего тиристора. Интервал проводимости тиристора от до π. Ток нагрузки прерывен.

Регулировочные характеристики трехфазного мостового выпрямителя, построенные по выражениям (59), (60), приведены на рис. 31, в. Неоднозначность регулировочных характеристики и зона прерывистого тока могут быть устранены путем шунтирования нагрузки обратным диодом. Регулировочная характеристика при этом будет аналогична характеристике работы на активную нагрузку, а зона прерывистого тока в нагрузке в пределе будет сужена до нуля за счет замыкания тока в контуре, содержанием э.д.с. нагрузки и обратный диод.

Однофазный выпрямитель с нулевым отводом

ИСТОЧНИКИ ВТОРИЧНОГО ЭЛЕКТРОПИТАНИЯ

ЭЛЕКТРОННЫХ УСТРОЙСТВ

Структурная схема источников вторичного электропитания

Источниками вторичного электропитания называются устройства, предназначенные для преобразования энергии первичного источника электропитания, которым, в частности, является сеть переменного тока, в электрическую энергию питания различных видов потребителей этой энергии. Одним из таких потребителей энергии является электронная аппаратура, для которой, как правило, требуется постоянное напряжение высокой стабильности с определенным номинальным значением. Например, электронная аппаратура, использующая интегральные микросхемы, требует для своего питания постоянного напряжения низкого уровня (± 5 — ± 15 В) при стабильности (± 5 – 10)%. Источники вторичного питания электронной аппаратуры строятся с использованием электронных приборов.

Рисунок 6.1. Структурная схема и временные диаграммы

напряжения источников вторичного питания

на входе и выходе его узлов

Структурная схема типового источника вторичного электропитания электронной аппаратуры приведена на рис.6.1. Она включает сетевой трансформатор (Т), выпрямитель (В), фильтр пульсаций (Ф) и стабилизатор выходного напряжения (СН). На этом же рисунке показана последовательность преобразования сетевого напряжения. Стабилизатором осуществляется не только изменение напряжения сети до необходимого уровня, но и гальваническая изоляция нагрузки от силовой сети. Выпрямитель, который является основным узлом источника вторичного питания, обеспечивает однонаправленное протекание тока, характеризующегося определенным уровнем пульсаций. В качестве вентиля в нем используются электронные приборы, обладающие свойством односторонней проводимости. Фильтром ослабляются пульсации напряжений на выходе выпрямителя. С этой целью используются фильтры низких частот на базе пассивных, а иногда и активных элементов. Стабилизатор напряжения предназначен для устранения влияния на выходное напряжение источника вторичного электропитания внешних воздействий, к числу которых относятся изменения напряжения сети и параметров нагрузки. В состав источников вторичного питания также могут включаться различные вспомогательные элементы и узлы, предназначенные для контроля, автоматики и защиты.

В зависимости от вида источников первичного питания существуют однофазные и трехфазные выпрямители. Выпрямителями, которые называются управляемыми, также может осуществляться регулировка выпрямленного напряжения. Ниже рассматриваются схемы однофазных неуправляемых выпрямителей.

Однофазный выпрямитель с нулевым отводом

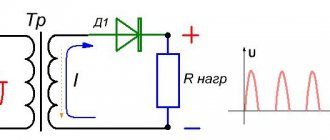
Схема однофазного выпрямителя с нулевым отводом от вторичной обмотки трансформатора представлена на рис. 6.2. В ее состав входит силовой трансформатор с расщепленной вторичной обмоткой, которая состоит из двух одинаковых половин. С каждой из половин этой обмотки снимаются напряжения, одинаковые по величине, но сдвинутые по фазе на 180° относительно нулевой точки, а также два диода Д1 и Д2.

Рисунок 6.2. Схема однофазного выпрямителя с нулевым отводом

Принцип работы выпрямителя рассматривается для случая активной нагрузки RH . При этом используются временные диаграммы напряжений и токов, которые приведены на рис.6.3. На рис.6.3,а и 6.3,б представлены временные зависимости подводимого от сети напряжения u1 , поступающего на первичную обмотку трансформатора, и напряжений u2-1 и u2-2 , снимаемых с каждой из половин вторичной обмотки. Для получения полного представления о работе выпрямителя вполне достаточно рассмотреть процессы, происходящие в выпрямителе в интервале фаз от 0 до , т.е. в течение одного периода подводимого напряжения.

Рисунок 6.3. Временные диаграммы, иллюстрирующие работу

однофазного выпрямителя с нулевым отводом

В интервале фаз 0÷ , когда на входе трансформатора действует положительный полупериод напряжения, на анод диода Д1 подается положительное напряжение, а на анод диода Д2 – отрицательное. Поэтому диод Д1 находится в открытом состоянии, а диод Д2 – в закрытом. Ток в таких условиях протекает через верхнюю половину вторичной обмотки трансформатора, диод Д1 и нагрузку RН. В нагрузке создается напряжение, временная зависимость которого при пренебрежении падением напряжения в открытом диоде совпадает с временной зависимостью напряжения u2-1, что иллюстрируется «положительной полуволной» на рис.6.3,в. Амплитуды напряжений и одинаковы.

В интервале фаз ÷ на входе трансформатора действует отрицательный полупериод напряжения, и в открытом состоянии находится диод Д 2, а в закрытом – диод Д 1. Ток протекает через нижнюю половину вторичной обмотки трансформатора, диод Д 2 и нагрузку. При этом направление тока в нагрузке будет таким же, как и в интервале фаз 0y . Следовательно, в интервале фаз ÷ напряжение в нагрузке имеет также положительную полярность. На рис. 6.3,в, где приведена временная зависимость напряжения на выходе выпрямителя, указаны номера диодов, через которые протекает ток в определенные полупериоды питающего напряжения.

Ток , протекающий через нагрузку, определяется законом Ома

. (6.1)

Он имеет такую же временную зависимость, что и напряжение (рис.6.3,г).

Как видно из рис.6.3,в и 6.3,г, напряжение и ток на выходе выпрямителя имеет вид импульсов положительной полярности. Разложение периодических функций и в ряд Фурье позволяет выделить постоянную и переменные составляющие напряжения и тока. Для потребителя выпрямленного напряжения важна постоянная составляющая, которую можно определить как среднее значение напряжения .

Поскольку период выпрямленного напряжения соответствует интервалу фаз шириной , внутри которого напряжение изменяется как функция синуса, для его постоянной составляющей можно записать:

, (6.2)

где — действующее значение напряжения, снимаемого с одной из половин вторичной обмотки трансформатора. Аналогичное соотношение может быть записано для постоянной составляющей выпрямленного тока:

. (6.3)

Амплитуда тока в нагрузке

. (6.4)

Значения постоянных составляющих выпрямленных напряжения и тока на рис. 6.3,в и 6.3,г представлены горизонтальными сплошными прямыми.

Диоды находятся в открытом и закрытом состоянии попеременно, а через каждый диод ток протекает в течение одного полупериода питающего напряжения, как показано на рис.6.3,д, е. Поэтому величина среднего тока диода вдвое меньше среднего тока нагрузки.

. (6.5)

Амплитудные значения токов в диодах и нагрузке одинаковы.

Когда диод закрыт, к нему приложено отрицательное напряжение, величина которого изменяется по синусоидальному закону, как показано на рис.6.3,ж для диода Д1. Амплитуда этого напряжения равна удвоенной величине амплитуды напряжения, снимаемого с одной из половин вторичной обмотки трансформатора, так как к закрытому диоду подводится напряжение с двух крайних отводов этой обмотки. Следовательно, максимальная величина обратного напряжения, которую должен выдерживать диод,

. (6.6)

Соотношения (6.5) и (6.6) используются при выборе типа диода, который предполагается применить в выпрямителе.

Качество выпрямленного напряжения оценивается параметром, называемым коэффициентом пульсации , который определяется как отношение амплитуды -ой гармоники выпрямленного напряжения к значению постоянной составляющей напряжения . Величины амплитуд гармонических составляющих напряжения определяются разложением в ряд Фурье функции

Наибольшую амплитуду имеет первая гармоника, для которой коэффициент пульсации

(6.8)

При частоте сети = 50 Гц частота первой гармоники на выходе выпрямителя составляет 100 Гц.

Модели неуправляемых и управляемых выпрямителей

Работа приведенного на рис.3.10 управляемого выпрямителя сводится к циклической смене двух типов состояний схемы:

1). Состояние проводимости, когда открыты два тиристора (тиристор VSA

(
a
) анодной (
а
) группы фазы
А
и тиристор
VSВ
(
к
) катодной (
к
) группы фазы
В
) и нагрузка находится под линейным напряжением
еАВ
(рис.3.11,а);

2). Состояние коммутации, когда открыты три тиристора (тиристор VSA

(
a
) анодной (
а
) группы фазы
А
, тиристор
VSВ
(
к
) катодной (
к
) группы фазы
В
и тиристор
VSС
(
к
) катодной (
к
) группы фазы
С
) и происходит коммутация токов в двух тиристорах (рис.3.11,б) – вводимом в работу
VSС
(
к
) и выводимом
VSВ
(
к
).

Рисунок 3.10 — Схема управляемого выпрямителя

На рис.3.11 открытые тиристоры изображены перемычками отмечены ток нагрузки iH

, ток коммутации
iК
во вводимом в работу тиристоре
VSС
(
к
) и ток коммутации
iδ
в выводимом из работы тиристоре
VSВ
(
к
).

Рисунок 3.11 — Состояния схемы трехфазного мостового управляемого выпрямителя

Схема коммутации (рис.3.11,б) описывается системой уравнений:

или

(3.21)

Схема в состоянии проводимости (рис.3.11,а) описывается системой уравнений

(3.22)

Объединение выражений (3.21) и (3.22) для двух состояний схемы дает

(3.23)

где F1

и
F7
— функции состояния схемы (ключи), принимающих значения
0
или
1
, причем функцией
F1
определяется интервал проводимости (при
F1=1
), а функцией
F7
— интервал коммутации (при
F7=1
).

Обобщением выражения (3.23) на все возможные состояния схемы на рис.3.10 является

(3.24)

где eH=

(
F1-F4
)
eAB+
(
F3-F6
)
eBC+
(
F5-F2
)
eCA
– обобщенная э.д.с., приложенная к нагрузке;

eK=

(
F1-F4
)
eBC+
(
F3-F6
)
eCА+
(
F5-F2
)
eAB
– обобщенная э.д.с., действующая в цепи коммутации.

При моделировании удобно вместо аргумента – времени t

использовать переменную фазы
θ
, которая связана с временем зависимостью
θ=ωt
. Тогда в системе (3.24) индуктивность
L
будет заменена на индуктивное сопротивление
X
в соответствии с соотношением
X=ωt
. Система (3.24) примет вид

(3.25)

Графики функций состояния F1…F7

приведены на рис.3.12. Функциями
F1…F6
задаются интервалы проводимости схемы в разных ее состояниях, а функцией
F7
задаются интервалы коммутации.

На рис.3.12 обозначено: α

— угол управления выпрямителя,
λ
— угол проводимости в течение такта работы схемы,
γ
— угол коммутации тиристоров. Окончание коммутации тиристров определяется моментом времени, когда ток
iδ
обращается в ноль. На интервалах коммутации ненулевой является только функция
F
предыдущего интервала проводимости.

Модель неуправляемого выпрямителя является частным случаем управляемого, когда угол управления α

равен
0
.

Рисунок 3.12 — Функции состояния схемы, значения ен и ек на интервалах проводимости и значения углов α, γ и λ

Вопросы для самоконтроля

1. Какие существуют состояния схемы управляемого выпрямителя?

2. Приведите систему уравнений для состояния коммутации схемы управляемого выпрямителя.

3. Приведите систему уравнений для состояния проводимости схемы управляемого выпрямителя.

4. Как определяется значение обобщенной э.д.с., приложенной к нагрузке?

5. Как определяется значение обобщенной э.д.с., приложенной к цепи коммутации?

6. Поясните процедуру замены в модели аргумента времени t на аргумент углаθ .

7. Поясните графики, приведенные на рис.3.12.

Литература [1-9]

3.8 Методика моделирования устройств преобразовательной техники

Работа устройств преобразовательной техники сводится к циклической смене конечного числа состояний схемы. Так как отдельные состояния схемы подобны друг другу, то возможно обобщенное описание схемы одной системой уравнений, в которую вводятся переменные-функции состояния (ключи). Тогда перебор всех состояний схемы сводится к перебору значений функций состояния, а не схем и систем уравнений, что, конечно, существенно упрощает моделирование.

Значения функций состояния зависит от номера такта в течение периода повторяемости схемы. Целесообразно ввести функцию номера такта, по значению которой согласно вышеприведенных графиков функций состояния можно определять значения этих функций. На рис.3.13 приведена такая программа и результат ее выполнения. В программе использована функция floor

(
X
) определения целой части числа
Х
. В приведенной программе вычисления ведутся по переменной
t
, которые легко могут быть преобразованы в вычисления по переменной
θ
.

Рисунок 3.13 — Программа вычисления функции n

(
t
) номера такта в периоде

повторяемости состояний преобразовательного устройства

Далее решается обобщенная система уравнений с определением в процессе счета значений функций состояния. Методы расчета функций состояния в зависимости от t

или от
θ
для различных типов преобразовательных устройств имеют как много общего, так и имеют особенности, обусловленные спецификой схем и алгоритмов их работы.

Моделирование автономного инвертора напряжения

(
рис.3.7
)

Перепишем систему уравнений (3.19) в матричном виде

(3.26)

Решением системы (3.29) относительно переменных piA, piB, piC

является матрица
S
(
t,i
) размером
3х1
, которая определяется в пакете MathCAD с помощью стандартной функции
lsolve
решения системы линейных уравнений:

(
t,i
)
:=lsolve
(
M
(
t),N
(
t,i
)) (3.27)

Решение S

(
t,i
) имеет нормальную форму Коши и, поэтому оно может использоваться в стандартной функции
Rkadapt
решения системы дифференциальных уравнений:

z:=Rkadapt

(
iНАЧ, tНАЧ , tКОН , NВЫВ , S
(
t,i
)), (3.28)

где iНАЧ

— вектор начальных условий для токов
iА
,
iВ
и
iС
.

Значения функций состояния могут быть определены в соответствии с табл.3.1 и рис.3.13 выражениями

(3.29)

Из этих выражений значения функций переключения определятся как

(
t
)
=F
(
t
)
0, F2
(
t
)
=F
(
t
)
1, F3
(
t
)
=F
(
t
)
2,
F4

(
t
)
=F’
(
t
)
0, F5
(
t
)
=F’
(
t
)
1, F6
(
t
)
=F’
(
t
)
2
(3.30)

Если учесть вытекающие из табл.3.1 равенства

(
t
)
+F2
(
t
)
+F3
(
t
)
=0, F4
(
t
)
+F5
(
t
)
+F6
(
t
)
=0
(3.31)

то выражения (3.29) могут быть упрощены — вместо расчета матриц из трех строчек достаточно рассчитать матрицы из двух строчек, например F1

(
t
)
, F2
(
t
) и
F4
(
t
)
, F5
(
t
).

Моделирование управляемого выпрямителя

(
рис.3.10
)

Выход на функцию решения дифференциальных уравнений вида (3.28) такой же как и при моделировании АИН.

Аргументом всех функциональных зависимостей является переменная θ

с произвольным диапазоном изменения. Из нее образуется переменная
φ
(
θ
) с диапазоном изменения равным
2π
:

(3.32)

Линейные напряжения будут вычисляться по формулам

(3.33)

Так как графики функций состояния для выпрямителя (рис.3.12) существенно отличаются от графиков для АИН (рис.3.8), то и способ их определения для выпрямителя будет существенно иным, чем для АИН, задаваемым выражениями (3.29), (3.30) и (3.31).

Выполняются следующие вычисления:

1). Задается строчная матрица F0:=|0 0 0 0 0 0 0

|, которая транспонированием
F:=F0T
превращается в столбцовую матрицу
F
.

2). Вычисляется индекс n1

(
θ
) активного линейного напряжения в фазе коммутации тиристоров

(3.34)

3). Определяется момент формирования открывающего импульса на тиристор и одновременно начало процесса коммутации тиристоров

(3.35)

Для того, чтобы было выполнено равенство , необходимо задавать значение α

кратным шагу изменения угла
θ
.

4). Определяется момент завершения коммутации тиристоров и переход в состояние проводимости схемы

(3.36)

Вопросы для самоконтроля

1. Как определяется помер n

(
t
)
такта состояния схемы в функции текущего времени t?
2. Как приводится система дифференциальных уравнений модели АИН к нормальной форме?

3. Составьте формулы для определения значений функции состояния F1 , F2 и F3 модели АИН в зависимости от номера такта n

(
t
).

4. Составьте формулы для определения значений функции состояния F4 , F5 и F6 модели АИН в зависимости от номера такта n

(
t
).

5. Приведите формулу преобразования угла θ, который изменяется в произвольном диапазоне к углу φ

(
θ
)
с диапазоном изменения от 0 до 2π.
6. Поясните алгоритм вычислений, применяемых при моделировании выпрямителей.

Литература [1-9]

1). Состояние проводимости, когда открыты два тиристора (тиристор VSA

2). Состояние коммутации, когда открыты три тиристора (тиристор VSA

Рисунок 3.10 — Схема управляемого выпрямителя

На рис.3.11 открытые тиристоры изображены перемычками отмечены ток нагрузки iH

Рисунок 3.11 — Состояния схемы трехфазного мостового управляемого выпрямителя

Схема коммутации (рис.3.11,б) описывается системой уравнений:

или

(3.21)

Схема в состоянии проводимости (рис.3.11,а) описывается системой уравнений

(3.22)

Объединение выражений (3.21) и (3.22) для двух состояний схемы дает

(3.23)

где F1

Обобщением выражения (3.23) на все возможные состояния схемы на рис.3.10 является

(3.24)

где eH=

(
F1-F4
)
eAB+
(
F3-F6
)
eBC+
(
F5-F2
)
eCA
– обобщенная э.д.с., приложенная к нагрузке;

eK=

(
F1-F4
)
eBC+
(
F3-F6
)
eCА+
(
F5-F2
)
eAB
– обобщенная э.д.с., действующая в цепи коммутации.

При моделировании удобно вместо аргумента – времени t

(3.25)

Графики функций состояния F1…F7

На рис.3.12 обозначено: α

Модель неуправляемого выпрямителя является частным случаем управляемого, когда угол управления α

равен
0
.

Рисунок 3.12 — Функции состояния схемы, значения ен и ек на интервалах проводимости и значения углов α, γ и λ

Вопросы для самоконтроля

1. Какие существуют состояния схемы управляемого выпрямителя?

2. Приведите систему уравнений для состояния коммутации схемы управляемого выпрямителя.

3. Приведите систему уравнений для состояния проводимости схемы управляемого выпрямителя.

4. Как определяется значение обобщенной э.д.с., приложенной к нагрузке?

5. Как определяется значение обобщенной э.д.с., приложенной к цепи коммутации?

6. Поясните процедуру замены в модели аргумента времени t на аргумент углаθ .

7. Поясните графики, приведенные на рис.3.12.

Литература [1-9]

3.8 Методика моделирования устройств преобразовательной техники

Рисунок 3.13 — Программа вычисления функции n

(
t
) номера такта в периоде

повторяемости состояний преобразовательного устройства

Моделирование автономного инвертора напряжения

(
рис.3.7
)

Перепишем систему уравнений (3.19) в матричном виде

(3.26)

Решением системы (3.29) относительно переменных piA, piB, piC

(
t,i
)
:=lsolve
(
M
(
t),N
(
t,i
)) (3.27)

Решение S

z:=Rkadapt

(
iНАЧ, tНАЧ , tКОН , NВЫВ , S
(
t,i
)), (3.28)

где iНАЧ

— вектор начальных условий для токов
iА
,
iВ
и
iС
.

Значения функций состояния могут быть определены в соответствии с табл.3.1 и рис.3.13 выражениями

(3.29)

Из этих выражений значения функций переключения определятся как

(
t
)
=F
(
t
)
0, F2
(
t
)
=F
(
t
)
1, F3
(
t
)
=F
(
t
)
2,
F4

(
t
)
=F’
(
t
)
0, F5
(
t
)
=F’
(
t
)
1, F6
(
t
)
=F’
(
t
)
2
(3.30)

Если учесть вытекающие из табл.3.1 равенства

(
t
)
+F2
(
t
)
+F3
(
t
)
=0, F4
(
t
)
+F5
(
t
)
+F6
(
t
)
=0
(3.31)

(
t
)
, F2
(
t
) и
F4
(
t
)
, F5
(
t
).

Моделирование управляемого выпрямителя

(
рис.3.10
)

Выход на функцию решения дифференциальных уравнений вида (3.28) такой же как и при моделировании АИН.

Аргументом всех функциональных зависимостей является переменная θ

с произвольным диапазоном изменения. Из нее образуется переменная
φ
(
θ
) с диапазоном изменения равным
2π
:

(3.32)

Линейные напряжения будут вычисляться по формулам

(3.33)

Выполняются следующие вычисления:

1). Задается строчная матрица F0:=|0 0 0 0 0 0 0

|, которая транспонированием
F:=F0T
превращается в столбцовую матрицу
F
.

2). Вычисляется индекс n1

(
θ
) активного линейного напряжения в фазе коммутации тиристоров

(3.34)

(3.35)

Для того, чтобы было выполнено равенство , необходимо задавать значение α

кратным шагу изменения угла
θ
.

4). Определяется момент завершения коммутации тиристоров и переход в состояние проводимости схемы

(3.36)

Вопросы для самоконтроля

1. Как определяется помер n

(
t
).

5. Приведите формулу преобразования угла θ, который изменяется в произвольном диапазоне к углу φ

Литература [1-9]