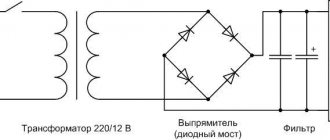
Составление схем прямой, обратной и нулевой последовательностей

Составление схем прямой, обратной и нулевой последовательностей

Схема прямой последовательности является обычной схемой, которую составляют при любом симметричном режиме.

Схема обратной последовательности по структуре аналогична схеме прямой последовательности, поскольку пути циркуляции токов обратной последовательности те же, что и токов прямой последовательности. Различие между ними состоит в том, что в схеме обратной последовательности эдс

всех генерирующих ветвей принимаются равными нулю и, кроме того, считают, что сопротивления обратной последовательности синхронных машин и нагрузок практически постоянны и не зависят от вида и условий возникшей несимметрии, а также от продолжительности переходного процесса.

Началом схемы прямой или обратной последовательности считают точку, в которой объединены свободные концы всех генерирующих и нагрузочных ветвей; это точка нулевого потенциала схемы соответствующей последовательности.

Концом схемы прямой или обратной последовательности считают точку, где возникла рассматриваемая несимметрия.

При необходимости учета емкостной проводимости последняя должна быть введена аналогично нагрузочной ветви, потенциал свободного конца которой равен нулю.

Схема нулевой последовательности в значительной мере определяется соединением обмоток имеющихся в схеме трансформаторов и автотрансформаторов. Токи нулевой последовательности по существу являются однофазным током, разветвленным между тремя фазами и возвращающимся через землю и параллельным ей цепям.

Чтобы составить схему замещения нулевой последовательности, следует допустить, что в точке несимметричного кз

все фазы соединены между собой накоротко и между этой точкой и землей приложено напряжение нулевой последовательности. Затем, идя от точки
кз
поочередно в разные стороны, необходимо на каждой ступени напряжения исходной расчетной схемы выявить возможные пути циркуляции токов нулевой последовательности (циркуляция этих токов возможна только в тех ветвях, которые образуют контуры для замыкания токов через землю и параллельные ей цепи) и соответственно определить элементы этой схемы, которые должны быть введены в схему замещения. При этом следует иметь в виду, что сопротивление нулевой последовательности трансформатора со стороны обмотки, соединенной в треугольник или звезду с незаземленной нейтралью, бесконечно велико, поэтому трансформаторы с указанными схемами соединения и все находящиеся за ними элементы исходной расчетной схемы в схему замещения нулевой последовательности не входят.

Циркуляция токов нулевой последовательности возможна только в том случае, если обмотка трансформатора, обращенная в сторону расчетной точки кз

, соединена в звезду с заземленной нейтралью.

Сопротивление, через которое заземлена нейтраль трансформатора, генератора, двигателя, нагрузки, должна быть введено в схему нулевой последовательности утроенной величиной.

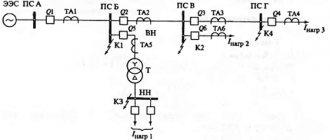
Процедуру составления схем замещения последовательностей при несимметричном коротком замыкании рассмотрим для исходной расчетной схемы электроустановки, приведенной на рис. 9.11.

Рис. 9.11. Исходная расчетная схема электроустановки

Схема замещения для первой последовательности приведена на рис. 9.12. В схеме сопротивление ВЛ для токов первой последовательности XЛ1=Xуд1ˑL, где Xуд1 – удельное сопротивление первой последовательности ВЛ, U

k1 – напряжение первой последовательности в точке
кз
; параметры остальных элементов схемы те же, как и при расчете симметричных коротких замыканий.

Рис. 9.12. Схема замещения первой последовательности

Рис.9.13. Преобразованная схема

замещения первой последовательности

В преобразованная схеме замещения первой последовательности, представленной на рис. 9.13:

Уравнение контурного тока для преобразованной схемы замещения прямой последовательности

Схема замещения и преобразованная схема обратной последовательности представлены на рис. 9.14 а

,
б
.

Уравнение контурного тока для преобразованной схемы замещения запишется в виде:

б

– преобразованная

Сопротивления обратной последовательности в схеме замещения такие же как и для прямой последовательности за исключением сопротивления синхронного генератора.

Эдс обратной последовательности для СГ и генераторов системы существовать не может, т.к. это означало бы, что генераторы должны изменить направление вращения роторов, что физически невозможно.

Схема замещения и преобразованная схема нулевой последовательности представлена на рис. 9.15.

В схеме замещения Xл0 = Xуд0 · L – сопротивление ВЛ токам нулевой последовательности, Xт10, Xт20 – сопротивления трансформаторов токам нулевой последовательности. В преобразованной схеме эквивалентное сопротивление нулевой последовательности определяется по формуле

Рис. 9.15. Схема замещения нулевой последовательности: а

– исходная,
б
– преобразованная

Уравнение контурного тока для преобразованной схемы нулевой последовательности

В схеме замещения нулевой последовательности эдс

нулевой последовательности источников, также как и в схеме замещения обратной последовательности, равны нулю.

Определение симметричных составляющих в фазных и междуфазных напряжений: расчет, формулы

Обратная последовательность

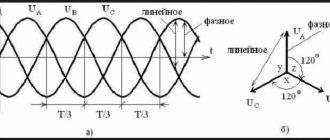
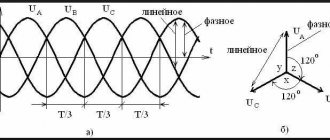
На рис. П6.1 изображены в виде звезды системы векторов междуфазных напряжений UАВ, UВC, UCA и напряжений прямой UАВ (1), UВC (1), UCA (1) и обратной UАВ (2), UВC (2), UCA (2) последовательностей. За действительную ось принят вектор UАВ (1). Вектор UАВ (2) сдвинут относительно вектора UАВ (2) на угол ϕ2 . Вектора UВC (2) и UCA (2) сдвинуты относительно векторов UВC (1) и UCA (1) на углы ϕ2 – 120° и ϕ2 + 120° соответственно.

Рис. П6.1. Междуфазные напряжения и их симметричные составляющие

Связь модулей междуфазных напряжений UАВ ≠ UВC ≠ UCA и модулей напряжений прямой U1 = UАВ (1) = UВC (1) = UCA (1) и обратной U2 = = UАВ (2) = UВC (2) = UCA (2) последовательностей выражается системой трех уравнений, содержащих три неизвестных – U1 , U2 и ϕ2 :

Возводя каждое уравнение системы (П6.1) в квадрат и используя тригонометрические формулы для косинусов и синусов сумм и разностей аргументов:

получим систему уравнений:

Для исключения величин U1 2 и U2 2 вычтем третье уравнение из первого и второго уравнения и получим систему двух уравнений:

Определяя из каждого уравнения (П6.4) величину U2 и приравнивая полученные выражения, получим:

откуда непосредственно следует:

Если знаменатель формулы (П6.6) меньше нуля, к углу ϕ2 надо прибавить 180°.

Для упрощения записи последующих уравнений введем следующие обозначения:

Из соотношения тригонометрических функций и с учетом принятых обозначений имеем:

Из второго уравнения (П6.4) имеем:

Подставив (П6.9) в первое уравнение (П6.4), получим выражение для cos ϕ2 через другие величины:

Приравнивая (П6.8) и (П6.10), получим связь величин U1 и U2 :

Подставив (П6.8) и второе уравнение (П6.11) в первое уравнение системы (П6.3), получим биквадратное уравнение:

решение которого дает окончательную формулу:

Если подставить в (П6.3) не второе, а первое уравнение (П6.11), то получим формулу для U2 , правая часть которой полностью совпадает с (П6.13). Это не удивительно, так как формулы (П6.3) инвариантны по отношению к величинам U1 и U2 : при одновременной замене U1 на U2 и U2 на U1 формулы не изменяются. Поэтому при знаке «+» перед внутренним корнем в формуле (П6.13) по ней 402 определяется величина, имеющая большее значение, а при знаке «–» – меньшее. Так как физически U1 > U2 , то общая формула имеет вид (8.6). Данные формулы были впервые выведены в 1985 г. [44].

Для проверки правильности полученных формул примем в качестве примера значения междуфазных напряжений, соответствующие U1 = 400 В; U2 = 40 В и ϕ2 = 30°. Подставив эти значения в формулы (П6.1), получим: UAB = 435,1 В; UBC = 402,0 В; UCA = 365,9 В.

Приняв эти напряжения в качестве исходных данных, по формулам (8.6) и (8.7) получим: U1 = 400 В; U2 = 40 В; ϕ 2 = 30° , что говорит о правильности формул.

Преобразования уравнений (П6.1) могут проводиться различными способами. Например, в [45] приведена формула для напряжения обратной последовательности, также использующая величины (П6.7) и определяющая значение U2 в процентах от U1 (формула для U1 в [45] не приведена, поэтому значение U2 в вольтах оказывается не определенным):

Подставив в формулу значения a4 и a2 , получим U2 (%) = 10 %.

Нулевая последовательность

В фазных напряжениях содержатся все три последовательности. Система уравнений, связывающая модули фазных напряжений с модулями напряжений прямой, обратной и нулевой последовательности, имеет вид:

В уравнениях (П6.15) пять неизвестных: U1ф, U2ф, U0 , ϕ2ф и ϕ0 . Получить выражения для них из системы трех уравнений невозможно. Поэтому рассчитать составляющие прямой, обратной и нулевой последовательностей фазных напряжений на основании измерения только фазных напряжений нельзя. Необходимо использовать полученные из расчета междуфазных напряжений составляющие прямой и обратной последовательности фазных напряжений: U1ф = = U1 / 3 и U2ф = U2 / 3 . Угол ϕ 2ф между U2ф и U1ф связан с углом 403 между U2 и U1 . соотношением ϕ 2ф = ϕ 2 + 60°, то есть также является известным. При этом в (П6.15) остается только два неизвестных: U0 и ϕ 0 . Система уравнений оказывается избыточной – достаточно использовать два любых уравнения. Тем не менее продолжим операции со всеми тремя уравнениями, так как вывод окончательных формул оказывается проще.

Для упрощения записи (П6.15) произведения и суммы уже известных величин и являющихся при выводе соотношений для U0 постоянными, обозначим:

Для упрощения дальнейших преобразований исключим величину U0 2 . Для этого вычтем из первого уравнения второе, а из второго третье уравнение и получим систему из двух уравнений:

Величины в круглых скобках формул (П6.20), являющиеся постоянными, для упрощения записи обозначим:

При этом формулы (П6.20) приобретут вид:

Выражая из каждого уравнения U0 и приравнивая правые части полученных формул, получим:

Равенство правых частей формулы (П6.23) запишем в виде:

Разделив числитель и знаменатель правой части равенства на cos ϕ0 , получим:

После определения угла ϕ0 значение U0 определяют, подставляя его в любое из уравнений (П6.23).

Приведенный алгоритм вычисления предполагает определение U0 после предварительного определения ϕ0 . Подставив (П6.25) в соотношения

и затем в (П6.23), можно получить формулу, непосредственно определяющую U0 через фазные и междуфазные напряжения, однако она получается чрезмерно громоздкой. Поэтому целесообразнее использовать последовательно формулы (П6.25) и (П6.23).

Подставив в (П6.21) выражения (П6.16), получим формулы, непосредственно связывающие величины a, b, c, d, e, f с определенными на первом этапе параметрами прямой и обратной последовательности (как в фазных, так и в междуфазных напряжениях):

Для проверки правильности полученных формул примем в качестве примера значения фазных напряжений, соответствующие U0 = 20 В, ϕ0 = 60° и полученным ранее из расчета междуфазных напряжений U1ф = 400 / 3 , U2ф = 40 / 3 и ϕ2ф = ϕ2 + 60° = 30° + 60° = 90°. Подставив эти значения в формулы (П6.15), получим:

По (П6.26) вычисляем коэффициенты:

Подставив эти данные последовательно в (П6.24), (П6.25) и (П6.23), получим:

что подтверждает правильность расчетных формул.

Все приведенные выше формулы получены исходя из первоначальных систем уравнений, связывающих фазные и междуфазные напряжения с напряжениями симметричных составляющих и углами между ними. Другой способ вывода подобных формул основан на использовании соотношений между сторонами и углами косоугольных треугольников.

Известны формулы, выведенные Ф. Ф. Карповым (приведены в «Методических указаниях по контролю и анализу качества электроэнергии в электрических сетях общего назначения», опубликованных в [46]), в соответствии с которыми параметры напряжения прямой и обратной последовательности определяют следующим образом:

где U′ и U″ с соответствующими нижними индексами – продольная и поперечная составляющие векторов U1 и U2 ; ϕ1(2)–AB – углы векторов U1 и U2 по отношению к вектору UBA. Если U′ 1(2) < 0, к ϕ1–AB и ϕ2–AB надо прибавить 180°. Угол вектора U2 относительно вектора U1 определяется разностью ϕ2–1 = ϕ2–AB – ϕ 1–АB.

Для определения значений U 1(2) и U  1(2) вначале рассчитывают вспомогательные величины:

а затем подставляют их в формулы:

В формулах (П6.29) при определении составляющих вектора U1 принимают знак «+», а вектора U2 – знак «–». Значения прямой и обратной последовательности, определенные по этим выражениям для условий примера, полностью совпадают с определенными выше, при этом углы ϕ1–АB = –2°40′; ϕ2–AB = 27°20′ и ϕ2 = ϕ2–AB – ϕ1–АB = 30°.

Параметры напряжения нулевой последовательности в соответствии с [46] определяют по формулам:

Для определения значений U′ 0 и U″ 0 дополнительно к величинам (П6.28) рассчитывают вспомогательные величины:

а затем подставляют все вспомогательные величины в формулы:

При преобразовании соотношений между сторонами и углами косоугольных треугольников могут использоваться различные приемы. Полученные при этом расчетные формулы могут иметь различный внешний вид, однако если при их выводе не использовались допущения (например, пренебрежение какими-либо составляющими вследствие их заведомой малости по сравнению с остальными), то все формулы дают идентичные результаты.

В частности, в ГОСТ 13109–97 [47] приведены формулы (в формуле для U0 исправлены знаки перед X и Y):

К сожалению, к этим относительно простым по виду выражениям нет формул для определения углов между векторами симметричных составляющих. Для целей сопоставления рассчитанных величин с нормами стандарта углы не нужны, однако при выборе средств симметрирования режима (например, расчета мощности конденсаторов по фазам) без них обойтись нельзя.

Все приведенные выше формулы являются точными алгебраическими выражениями, дающими абсолютно идентичные результаты. При экспресс-оценке симметричных составляющих по результатам измерения без применения сложных формул можно использовать приближенные соотношения:

При различных значениях угла ϕ2 коэффициент во второй формуле не выходит за пределы 0,575–0,665, поэтому максимальная погрешность приближенного определения U2 не превышает 7,3 %. Погрешность приближенного определения U1 еще меньше, причем среднее значение междуфазных напряжений всегда несколько больше фактического значения U1 . Это превышение зависит от значения U2 и хорошо аппроксимируется формулой δU1 (%) = 0,0025 U2 (%) 2 . Например, при U2 = 2 % превышение составит всего 0,01 %, а при U2 = 10 % – 0,25 %.

Для приведенного примера по формулам (П6.35) получаем: U1 = = 401 В и U2 = 42,9 В (U2 (%) = 10,7 %). Если уточнить значение U1 вычитанием превышения δU1 = 0,0025 ∙ 10,72 ∙ 401 = 1,15 В, то U1 = 399,85 В, то есть U1 определяется с погрешностью менее 0,04 %.

Балансировка фазных и междуфазных напряжений

Необходимость такой балансировки обоснована в п. 8.1.2. Вид уравнений корректировки измеренных напряжений с целью приведения их к физически существующей системе зависит от принятого критерия балансировки. Возможны следующие критерии.

1. Оставить пять напряжений неизменными, а последнее фазное напряжение изменить так, чтобы оно пришло в нулевую точку, определенную двумя другими фазными напряжениями (см. рис. 8.4, в). Обоснованность такого подхода сомнительна, так как неясно, по какому условию должно выбираться единственное «неточное» напряжение, требующее корректировки.
2. Осуществлять корректировку всех фазных напряжений, оставив неизменными междуфазные напряжения. В этом случае встает вопрос, почему междуфазные напряжения следует считать точными, а фазные – неточными?
3. Так как все шесть напряжений измерены с погрешностью, представляется более логичным, что все они должны быть подвергнуты корректировке. При этом направленность корректировки фазных 409 и междуфазных напряжений оказывается различной. В случае, изображенном на рис. 8.4, а, междуфазные напряжения должны быть несколько увеличены, а фазные уменьшены, а в случае, изображенном на рис. 8.4, б, – наоборот. Считая, что все напряжения измерены прибором с одинаковой относительной погрешностью δ, представляется логичным, что все шесть напряжений должны быть изменены в одинаковой пропорции (хотя и в разные стороны). При таком подходе встает вопрос: почему предполагается, что при измерении всех междуфазных напряжений погрешность проявилась в одну сторону, а при измерении всех фазных напряжений – в другую?

К каждому из подходов имеются вопросы, которые, как кажется, полностью демонстрируют нелогичность рассмотренных подходов. Тем не менее задача состоит не в опровержении подходов, а в предложении хотя бы одного приемлемого, так как проводить расчеты симметричных составляющих для физически несуществующей системы исходных векторов еще более нелогично.

Условием физического существования системы является равенство ϕАВ + ϕВС + ϕСА = 360° (на рис. 8.4, а сумма фактических углов больше 360°, а на рис. 8.4, б – меньше 360°).

Из известных соотношений сторон и углов косоугольных треугольников угол ϕАВ определяется по формуле

Аналогичные выражения могут быть записаны и для углов ϕВС и ϕСА . Сумма половинных углов, естественно, должна быть равна 180°. Определенная же по измеренным напряжениям, она всегда будет отличаться от этой величины. Степень отличия охарактеризуем соотношением:

Значения напряжений в формуле (П6.37) необходимо скорректировать таким образом, чтобы определенные по (П6.37) углы удовлетворяли условию kϕ = 1. Это условие может быть обеспечено при различном изменении углов, входящих в сумму. Критерий корректировки углов неочевиден: корректировать ли все углы в одинаковой степени или в большей пропорции изменять меньшие углы (или наоборот)? Из описанных выше подходов наименьшие недостатки присущи третьему. Выведем соотношения для корректировки напряжений исходя из этого подхода и условия корректировки всех углов в одинаковой степени: к / i i k ϕ =ϕ ϕ .

Для того, чтобы угол ϕАВ, определяемый по формуле (П6.37), стал равным к ϕAB , необходимо изменить напряжения UAB, UA, UB в соответствии с равенством

Аналогичные коэффициенты могут быть определены и для двух других треугольников. Коэффициенты будут отличаться друг от друга, что объясняется принятым допущением о корректировке всех углов в одинаковой пропорции. Вместе с тем в каждом треугольнике две стороны являются общими для смежных треугольников и не могут корректироваться по-разному. Единственным видимым выходом является применение ко всем напряжениям среднего коэффициента корректировки kU = (kU AB + kU BC + kU CA ) / 3.

Для примера предположим, что в результате измерений получены следующие напряжения:

Вычислив по формуле (П6.37) и подобным формулам для других треугольников соответствующие углы, получим:

Сумма углов составляет 196,2°, то есть система соответствует случаю рис. 8.4, б. Необходимо уменьшить углы, разделив их на коэффициент kϕ = 196,2 / 180 = 1,09. При этом значения углов к / 2 ϕAB и соответствующих им тангенсов составят:

Подставляя эти значения tg ϕ в формулу (П6.40) и в подобные формулы, записанные для других междуфазных и фазных напряжений, получим:

Применив kU ср к измеренным напряжениям, получим:

Если определить по формулам типа (П6.37) углы для этой системы напряжений, то их сумма составит (65,1° + 64,8° + 48,3°) = = 178,2°, то есть вместо превышения на 16,2° сумма стала ниже необходимой на 1,8°. При желании можно сделать еще одну итерацию.

Для получения формулы корректировки напряжений для случая, когда начальная сумма углов оказывается меньше 180° (рис. 8.4, а), необходимо в формуле (П6.39) заменить деление на kU умножением, и наоборот. Однако, в связи с небольшим отличием значений kU от единицы, результат будет отличаться несущественно. Поэтому и в этом случае можно пользоваться формулой (П6.40); при этом значения kU окажутся чуть меньше единицы и приведут к необходимому увеличению междуфазных и уменьшению фазных напряжений.

При использовании приведенного алгоритма поставленная цель – создание физически существующей системы векторов – достигается. Однако остаются вопросы об обоснованности принятого критерия – изменение фазных и междуфазных напряжений в разные стороны. Учитывая случайный характер измеренных величин, представляется наиболее обоснованным использовать критерий минимума суммы квадратов отклонений относительных значений скорректированных напряжений от их измеренных значений:

при одновременном соблюдении условия, накладываемого на сумму углов. Решение такой системы уравнений в настоящее время отсутствует.

В целом алгоритм вычисления параметров симметричных составляющих состоит из следующих этапов:

• проводят балансировку фазных и междуфазных напряжений;
• вычисляют параметры прямой и обратной последовательности междуфазных напряжений по формулам (8.6) и (8.7) или другим аналогичным формулам;
• по формулам (8.8) вычисляют коэффициенты a, b, c, d, e, f; по формулам (8.9) – (8.11) вычисляют параметры нулевой последовательности.

Что такое напряжение нулевой последовательности? Схемы, применение, физический смысл

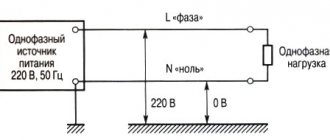
Система трехфазных напряжений в нормальном режиме работы является симметричной. Но, стоит произойти короткому замыканию, как симметрия нарушается. Для удобства распознавания видов КЗ и проведения расчетов применяется метод симметричных составляющих. Согласно ему любую трехфазную систему с момента КЗ можно, для удобства расчетов, представить в виде суммы напряжений трех симметричных систем:

Все они являются мнимыми величинами, не существующими на самом деле. Но с помощью некоторых ухищрений их можно сделать реально осязаемыми, и применить на практике.

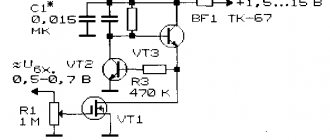
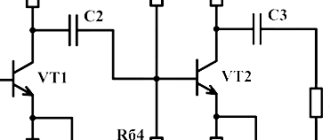
Устройства, выделяющие из системы трехфазных напряжений напряжение нужной последовательности, называют фильтрами. Рассмотрим одно из таких устройств, применяемое на практике для фиксации замыканий на землю.

Глава тридцать восьмая
НЕСИММЕТРИЧНЫЕ РЕЖИМЫ РАБОТЫ СИНХРОННЫХ ГЕНЕРАТОРОВ
§ 38-1. Действие симметричных составляющих токов в синхронной машине и параметры прямой, обратной и нулевой последовательности

Предварительные замечания.

На практике встречаются случаи, когда мощные однофазные потребители нарушают симметричную нагрузку фаз синхронных генераторов (тяговые подстанции железных дорог, электрифицируемых на переменном токе, и т. д.). Еще более часто, хотя и кратковременно, несимметричная нагрузка фаз генераторов возникает при несимметричных коротких замыканиях
в
электрических сетях: при однофазном коротком замыкании — между линейным и нулевым проводами, при двухфазном коротком

замыкании — между дв^мя линейными проводами и при двухфазном коротком замыкании на нейтраль — между двумя линейными и нулевым проводами. Роль нулевого провода в сетях высокого налряже-ния играет земля, так как нулевые точки в таких сетях обычно заземляются.

Хотя несимметричные короткие замыкания существуют кратковременно, так как поврежденные участки сетей отключаются релейной защитой, они оказывают сильное влияние на работу генераторов и сети в целом. При внезапных несимметричных коротких замыканиях возникают также переходные процессы, однако ниже для выявления главных особенностей явлений рассматриваются прежде всего установившиеся несимметричные режимы работы.

Общим методом исследования несимметричных режимов является метод симметричных составляющих, при котором несимметричная система токов раскладывается на симметричные составляющие и действие последних учитывается по отдельности. В данном параграфе рассмотрим действие токов равных последовательностей в трехфазной синхронной машине.

Токи и сопротивления прямой последовательности.

При симметричной нагрузке синхронного генератора существуют только токи прямой последовательности. Поэтому изложенное в гл. 32 и 33 относится к работе синхронных машин с токами прямой последовательности и введенные там синхронные сопротивления
xd
и
xq
являются сопротивлениями синхронной машины для токов прямой последовательности.

Наиболее существенной особенностью нормального режима работы синхронной машины с токами прямой последовательности является то, что ротор машины вращается синхронно с полем токов прямой последовательности или полем реакции якоря и поэтому это поле не индуктирует в цепях индуктора никаких токов. По этой причине сопротивления xd

и
xq
велики.

Пользуясь терминологией теории асинхронных мащин, можно сказать, что скольжение s ротора синхронной машины относительно магнитного поля токов прямой последовательности статора (якоря) равно нулю. Поэтому сопротивления ха

и
xq
идентичны с индуктивным сопротивлением асинхронной машины при идеальном холостом ходе (s =
sx =
0).

Составляющими этого сопротивления являются индуктивное сопротивление рассеяния хаа

и индуктивное сопротивление от основной гармоники поля в воздушном зазоре (для синхронной машины

Токи и сопротивления обратной последовательности.

Представим себе,
что
обмотка якоря (статор)
синхронной машины питается напряжением обратной последовательности U2.
Возникающие при этом токи обратной последовательности создают магнитное поле обратной последовательности, которое вращается по отношению к статору с синхронной скоростью в обратном направлении, а по отношению к ротору, вращающемуся с синхронной скоростью в прямом направлении, — с удвоенной синхронной скоростью. Поэтому относительно этого поля скольжение ротора s2

= 2 и в обмотках возбуждения, успокоительной и в массивных частях ротора индуктируются вторичные токи двойной частоты, которые вызывают соответствующие потери и нагрев ротора.

Ввиду сказанного для рассматриваемого случая действительно все изложенное в § 36-1 при s = 2.

Схемами замещения для токов обратной последовательности являются схемы рис. 36-2 при s = 2. Обозначим сопротивления этих схем при s =

2 буквами Zd2 и Zg2.

При Zd2 ф

Z92 токи статора содержат составляющую основной частоты и, согласно выражению (36-4), токи тройной частоты, влиянием которых можно пренебречь. Ток основной частоты представляет собой ток обратной последовательности /2 и определяется первым равенством (36-3) при
s = 2:
Поэтому в первом случае в соответствии с равенством (38-2)

Сопротивление Z2 по формуле (38-2) соответствует случаю, когда напряжения статора синусоидальны, а токи несинусоидальны Если последовательно с обмоткой статора включены значительные индуктивные сопротивления (например, сопротивления трансформаторов и линий передачи), то токи обратной последовательности синусоидальны, а напряжения обмотки статора несинусоидальны. В этом случае, как можно показать,

При этом высшие гармоники тока и напряжения отсутствуют.

Вследствие экранирующего влияния вторичных токов сопротивление *2 значительно меньше ха

и
xq
(см. табл. 32-1). Сопротивления 22, х2и
h
можно определить по измеренным значениям
U2,
/2 и потребляемой активной мощности
Р2,
если приключить синхронную

машину к источнику с

симметричной системой напряжений и вращать ротор против поля
с
синхронной скоростью. Во избежание перегрева ротора необходимо, чтобы /2 = (0,2 -г- 0,25) /н. Если машина не имеет успокоительных обмоток и контуров, то для получения более правильных результатов надо из осциллограмм выделить основные гармоники тока и напряжения.

Токи и сопротивления нулевой последовательности.

Токи нулевой последовательности обмотки статора /0 создают в воздушном зазоре только пульсирующие поля гармоник v = = 3, 9, 15…, а основная гармоника поля будет отсутствовать (см. § 22-2). Эти гармоники поля индуктируют в обмотках возбуждения и успокоительной токи, величины которых относительно невелики.

Сопротивление нулевой последовательности

Индуктивное сопротивление нулевой последовательности х0

ввиду отсутствия поля основной гармоники относительно невелико (см. табл. 32-1) и определяется полями пазового и лобового рассеяния обмотки статора и указанными выше гармониками поля в зазоре. Активное сопротивление нулевой последовательности
г0
в результате потерь, вызываемых гармониками поля в роторе, несколько больше активного сопротивления обмотки статора
га,
но разность
г0
—
га
невелика и г0
!=& га.
Вращающий момент, создаваемый токами /0, практически равен нулю.

Сопротивления г0, х0

и,
г0
можно определить опытным путем, если при вращении машины с синхронной скоростью питать после* довательно включенные фазы обмотки статора током /0. Указанные сопротивления при этом определяются точно так же, как и у трансформатора (см. §
16-1).
§ 38-2., Работа синхронных генераторов при несимметричной нагрузке

Обмотка статора синхронных генераторов обычно включается в звезду, причем нулевая точка в малых машинах изолирована, а в крупных машинах с целью выполнения релейной защиты от замыканий на землю заземляется через большое сопротивление. Поэтому токи нулевой последовательности либо отсутствуют, либо весьма невелики.

В силу этого при несимметричной нагрузке синхронных генераторов, кроме токоп прямой последовательности, практически существуют только токи обратной последовательности.

I Последние вызывают в машине ряд нежелательных явлений и делают режим работы машины тяжелым.

Потери энергии и нагрев ротора.

Токи двойной частоты, индуктируемые в роторе магнитным полем статора обратной последовательности, вызывают в роторе излишние потери и его нагрев, а также уменьшение к. п. д. машины.

Токи, индуктируемые -обратным полем в успокоительных обмотках явнополюсных машин и в массивном роторе турбогенераторов, могут быть весьма значительными, а активные сопротивления этим токам под влиянием поверхностного эффекта будут большими.

Поэтому при значительной несимметрии нагрузки возникает чрезмерный и опасный нагрев успокоительных обмоток и массивных роторов.

Высокая температура тела ротора турбогенератора вызывает опасные деформации ротора и вероятность повреждения изоляции обмотки возбуждения. Нагрев успокоительной обмотки явнополюс-ной машины мало влияет на температуру обмотки возбуждения ввиду удаленности этих обмоток друг от друга и лучших условий охлаждения обмотки возбуждения явнополюсных машин.

Токи, индуктируемые обратным полем в обмотке возбуждения, меньше из-за большего сопротивления рассеяния этой обмотки. Поэтому в явнополюсных машинах дополнительный нагрев обмотки возбуждения при несимметричной нагрузке невелик.

Вибрация.

В результате взаимодействия потока возбуждения и потока обратной последовательности статора, а также поля прямой последовательности статора и поля токов двойной частоты ротора при несимметричной нагрузке на ротор и статор действуют знакопеременные вращающие моменты и тангенциальные силы, пульсирующие с частотой 2/х.

Кроме того, вследствие этих же причин возникают пульсирующие радиальные силы притяжения и отталкивания между полюсами полей статора и ротора, стремящиеся деформировать статор и ротор. Эти силы вызывают вибрацию частей машины, шум и ослабление запрессовки сердечника статора. Пульсирующие силы двойной частоты ввиду усталостных явлений могут также вредно отразиться на прочности сварных соединений, в особенности при наличии дефектов сварки. Все указанные факторы, естественно, тем сильнее, чем больше несимметрия нагрузки.

Искажение симметрии напряжений.

Токи обратной последовательности вызывают в фазах обмотки статора падения напряжения

Z2/2, векторы которых ориентированы относительно напряжений прямой последовательности в разных фазах по-разному.

В результате этого симметрия напряжений генератора искажается и напряжения более загруженных фаз будут меньше. Это ухудшает условия работы приемников, в особенности асинхронных и синхронных двигателей.

В машинах с успокоительными обмотками и массивными роторами или полюсами Z2 меньше, вследствие чего и искажение симметрии напряжений у них меньше. Физически это объясняется тем, что в таких машинах поток обратной последовательности статора в значительной степени заглушается токами, индуктируемыми в роторе, и поэтому этот поток индуктирует в фазах обмотки статора меньшие э. д. с.

Высшие гармоники токов и
напряжений.
Как было установлено выше, ввиду неравенства сопротивлений по продольной
(Zdi)
и поперечной (Z?2) осям возникает третья гармоника тока с частотой 3/х- В особенности сильное искажение формы кривой ток,а происходит при несимметричных коротких замыканиях, так как при этом сглаживающее влияние внешних индуктивных сопротивлений исчезает или ослабляется. В качестве примера на рис. 38-1 изображена форма кривой тока при двухфазном коротком замыкании.

Высшие гармоники тока могут вызвать опасные резонансные явления, если в цепях обмоток статора имеются емкости (например, емкость длинных линий передачи и пр.).

В результате резонанса напряжений на зажимах обмотки статора возникают напряжения повышенных частот, которые могут превысить номинальные напряжения во много раз и повредить изоляцию машины. Это является одной из причин того, что мощные гидрогенераторы, работающие на длинные линии передачи, обычно снабжаются успокоительными обмотками. При наличии успокоительных обмоток Zrfam

Z?2 и
x»d
~
x»q,
вследствие чего в этом случае токи остаются синусоидальными и опасность указанных перенапряжений исчезает.

Допустимая несимметрия нагрузки ограничивается прежде всего необходимостью предотвращения опасного нагрева ротора, а также вибрации машины.

Согласно ГОСТ 183—66, допускается длительная работа турбо-и гидрогенераторов с

несимметричной нагрузкой, если токи фаз не превышают номинальных значений и разность токов в фазах не превышает 10% номинального тока фазы.

§ 38-3. Несимметричные короткие замыкания

Основные уравнения. Рассмотрим установившиеся несимметричные короткие замыкания на зажимах генератора с соединением обмоток в звезду в предположении, что они происходят при работе на холостом ходу, и определим величины токов коротких замыканий. Для этого составим прежде всего уравнения, связывающие между собой токи (/], /2, /0), * сопротивления (Z\,

22, Zo) и напряжения
(Ult U2, Uo)
разных последовательностей, причем
Ui, U2
и
Uo
являются» составляющими напряжений фаз
Ua, lib, Uc
в месте короткого замыкания (рис. 38-2).

Ток возбуждения индуктирует только э. д. с. прямой последовательности 1Ei

=
Е,
и поэтому £2 =
Еа
= 0. Так как цепи фаз вплоть до места короткого замыкания симметричны, то уравнения напряжений для разных последовательностей независимы друг от друга и для фазы
а
имеют вид

Кром« того, существуют следующие зависимости между токами и напряжениями фаз и их симметричными составляющими:

бенностей каждого вида короткого замыкания, необходимо составить три дополнительных уравнения.

Сначала целесообразно определить симметричные составляющие токов и напряжений, а затем по уравнениям (38-13) и (38-14) найти фазные величины.

Из уравнений (38-12) можно определить симметричные составляющие напряжений:

Если подставить эти значения Ult (]г, йа

в уравнения (38-14), то последние приобретают вид

Согласно выражениям (38-16), напряжения фаз равны э. д. с. фаз Ё, а2Ё

и
аЁ
минус падения напряжения от токов разных последовательностей в сопротивлениях соответствующих последовательностей.

Рис. 38-3. Схемы однофазного (а), двухфазного (б) и двухфазного на нейтраль (в) короткого замыкания синхронного генератора

Уравнения (38-12) — (38-16) действительны не только для несимметричных коротких замыканий, но и для общего случая несимметричной нагрузки синхронного генератора. Однако ниже он-и будут использованы для исследования несимметричных коротких замыканий.

Однофазные короткие замыкания.

В этом случае, согласно схеме рис. 38-3,
а,
или после подстановки значений а и о2

Рис. 38-6. Векторные диаграммы токов (а)

и напр-яжений (б) при двухфазном коротком замыкании на нейтраль

Комплексные схемы замещения. Полученные результаты позволяют составить для различных видов коротких замыканий весьма простые комплексные схемы замещения, которые включают в себя сопротивления различных последовательностей и определяют соотношения между токами и напряжениями различных последовательностей.

На рис. 38-7, а

на основании равенства (38-22) представлена такая схема для однофазного короткого замыкания. Генератор изображен в качестве источника э. д. с.
Е,
последовательно с ним соединено сопротивление прямой последовательности
Z%,
а между точками
М
и
N ,
условно изображающими место короткого замыкания, включены последовательно Z2 и Zo. Ниже мы увидим, что такая структура схемы сохранится и для других видов коротких замыканий, но в месте короткого замыкания, между точками
М и N,
будут действовать другие величины сопротивлений.

Очевидно,что схема рис. 38-7, а

вполне соответствует равенству (38-22). На этой схеме, кроме того, на основании уравнений (38-15) показано, между какими точками схемы действуют напряжения разных последовательностей. Как в данном,

так и в других случаях напряжение Ui

действует между условными точками короткого замыкания
М
и Л’, a
U2
и
Uo
равны падениям напряжения соответственно в сопротивлениях Z3 и
Zo.
На рис. 38-7, б

на основании равенства (38-28) представлена комплексная схема замещения для двухфазного короткого замыкания, а указанные там напряжения также определяются уравнениями (38-15). На рис. 38-7,
в
изображена схема для двухфазного короткого замыкания на нейтраль, соответствующая равенствам (38-36), а также (38-15) и (38-35). Наконец, на рис 38-7,
г,
согласно изложенному в § 33-2, изображена схема для трехфазного короткого замыкания. В этом случае

Рис. 38-7. Комплексные схемы замещения для однофазного (а),

двухфазного (б), двухфазного на нейтраль
(в)
и трехфазного (г) короткого замыкания синхронного генератора

Установив вид комплексных схем замещения, можно не решать уравнения, как это было сделано выше, а выписать выражения _ для 1и h> h

и
Ult U2, й0
непосредственно на основе схем замещения. Если на схеме сопротивление какой-либо последовательности отсутствует, то соответствующие составляющие тока и напряжения равны нулю Можно показать, что схемы рис. 38-7 действительны не только для рассмотренных простейших коротких замыканий, но и для несимметричных коротких замыканий в сложной сети, причем в последнем случае под Z1( Z2 и Zo нужно понимать сопротивления всей сети для токов соответствующих последовательностей.

Сравнение различных видов коротких замыканий.

Если сопротивление нулевого провода равно нулю и короткие замыкания происходят на зажимах машины, то
г1
> г2 > г0 или при пренебрежении активными сопротивлениями Zj =
х^
> г2 = =
х%
> г0 =
х0
(см. тйбл. 32-1). В этом случае на основании равенств (38-23), (38-29), (38-37) и (38-40) можно установить, что при одинаковых
Е
будет ^ki > ^кг > ^кго > ^кз- Физически это можно объяснить тем, что при однофазном коротком замыкании размагничивающую реакцию якоря создает только ток одной фазы и поэтому в данном случае величина тока короткого замыкания получается наибольшей, а по мере увеличения числа короткозамк-нутых фаз их токи уменьшаются. С другой стороны, как видно из схем рис. 38-7, для токов прямой последовательности действительны обратные соотношения: наибольшая величина /х соответствует трехфазному, а наименьшая — однофазному короткому замыканию. В соответствии со сказанным на рис. 38-8 изображены характеристики коротких замыканий.

При вычислении величин токов коротких замыканий всегда можно пользоваться соотношениями (38-24). Отметим, что, кроме рассмотренных выше токов

Рис. 38-8. Характеристики несимметричных и симметричных коротких замыканий синхронного генератора

основной частоты, при несимметричном роторе (отсутствие успокоительных обмоток и контуров) возникают также высшие гармоники токов.

Определение сопротивлений обратной последовательности. Данные опыта двухфазного короткого замыкания используются для определения г2, х2 и г2.

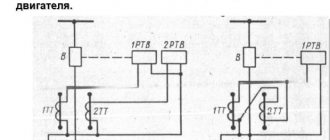
На рис. 38-9 показаны схемы двухфазного короткого замыкания с включением приборов для измерения необходимых величин, обозначения которых указаны рядом с условными изображениями приборов.

Рис. 38-9 Схемы для определения сопротивления обратной последовательности по данным опыта двухфазного короткого замыкания

Для модуля полного сопротивления по показаниям измерительных приборов на основании равенств (38-32) для схем рис. 38-9, а, б я в

соответственно

ПОЛУЧИМ

ГОСТ 10169—62 на испытание синхронных машин рекомендует использовать схему рис. 38-9, в

и последние из соотношений (38-41) и (38-42). Следует иметь в виду, что при отсутствии успокоительных обмоток и контуров получаемые

результаты из-за наличия высших гармоник будут неточными. Для учета влияния этих гармоник можно ввести поправки, которые здесь не рассматриваются. Определение сопротивлений нулевой последовательности. Для этой цели используются данные опыта двухфазного короткого замыкания на нейтраль, выполняемого согласно схеме рис. 38-10. В соответствии с равенством (38-39)

Рис. 38-10. Схема для определения сопротивлений нулевой последовательности по данным опыта двухфазного короткого замыкания на нейтраль

Внезапные несимметричные короткие замыкания.

Как и при внезапном трехфазном коротком замыкании, в этом случае также во всех обмотках возникают апериодические и периодические токи. При внезапных несимметричных коротких замыканиях периодические токи якорд будут содержать составляющие тех же последовательностей /х, 72, /0, как и при установившихся коротких замыканиях. Как вытекает из более подробного рассмотрения этого вопроса, амплитуды начальных значений периодических токов якоря можно вычислить по равенствам (38-23), (38-29) и (38-37), если подставить в них вместо Z\, 2г

и Zo соответственно
jxd
(или
jx’d),jx2
и
]х0
и умножить результаты на
Yi,
а амплитуды установившихся значений периодических токов вычисляются так же, но вместо
]x»d
(или
jxjfi
надо подставить /%• Разность начальных и конечных значений периодических токов затухает с постоянными времени
T’d, Та,
как и при трехфазном коротком замыкании, но при несимметричных коротких замыканиях эти постоянные имеют другие значения. Начальные значения апериодических токов якоря равны по величине и обратны по знаку периодическим токам и также затухают с соответствующими постоянными времени.

Более подробно внезапные несимметричные короткие замыкания рассматриваются в специальных руководствах [68, 69, 72, 73, 75, 76, 79J.

Содержание Предыдущий § Следующий