Lorentz force | Formula and definition

French physicist Marie Ampere surprised the world with many amazing discoveries. In particular, he proved the interaction of a conductor in a magnetic field with the strength of a given magnetic field in the presence of an electric current. From the school curriculum we know that current is the ordered movement of charged particles (electrons); accordingly, the electromagnetic field also affects an individual charged particle. This action is known in science as the Lorentz force; there is a certain formula in physics to determine its modulus.

History of discovery

Scientists first tried to determine what electromagnetic force is in the 18th century. Then experts suggested the following: the inverse square law can be applied to the force concentrated on the magnetic poles and on objects with a charge. However, it was not possible to practically prove this statement. This was done at the end of the 18th century by Charles Augustine de Coulomb, using a device for measuring minor forces, namely a torsion balance.

In the first half of the 19th century, discoveries were made that became the basis for the further development of the theory of electromagnetic fields. The following has been proven - the compass needle is under the influence of the magnetic force of the earth; in addition, a formula has been derived and proven for calculating the angular dependence between various current elements. These two discoveries became the basis for the theoretical developments of Michael Faraday; the scientist’s work was supplemented by calculations and specific justifications by Lord Kelvin and James Maxwell. The latter introduced the world of physics to Maxwell's field equation, which was used by Jay Thompson, and derived the value of the electromagnetic force acting on every charged moving particle. He formulated his theoretical conclusions with the formula: F = q/2 vx B. However, it turned out that it was not entirely correct.

Only at the end of the 19th century, the Dutch scientist Hendrik Lawrence managed to derive the correct formula; it is still used today, it is named after the scientist. The unit of measurement for Lorentz force is Newton.

Formulation and formulas

A particle with charge q experiences a force F when it moves with speed v in an electric (E) and magnetic (B) field. It is defined as F = qE + qv x B and is measured in SI units - N (newton). In terms of Cartesian components there are:

F x = q (E x + ⱴ y B z - ⱴ z B y);
F y = q (E y + ⱴ z B x - ⱴ x B z);
F z = q (E z + ⱴ x B y – ⱴ y B x).

E and B are functions of time position. Therefore, the equality can be written as F(r, ṙ, t, q) = q, where r is the position vector of the charged particle, t is time, and overdot is the derivative of time.

The acceleration of the particle will occur in the same linear orientation as the field E, but will begin to bend perpendicular to both the instantaneous velocity vector v and the field B. This indicates the correspondence of the Lorentz force formula and the “left-hand rule”. The "gimlet rule" will also apply here (if the fingers flare out to point towards v and then curl to point towards B, then the thumb will point towards F).

The combination q E is called the electric force, and q (v + B) is called the magnetic force. In this context, it can be called the Laplace force. It does not affect the power because it is always perpendicular to the particle speed.

For a continuous charge distribution in motion, the equation takes the form dE = dq (E + v + B). If both sides of the equation are divided by the volume of a small fragment dV, the result will look like this : f = p (E + vx B). Therefore, the continuous analogue of the equation is f = pE + J x B, where J is the current density.

The total force is the volume integral over the charge distribution: F = ∫∫∫ (p E + J x B) dV. By eliminating p and J, using Maxwell's equations, and manipulating using theorems of vector calculus, this form can be used to obtain the stress tensor σ. This in turn can be combined with the Poynting vector s to produce the electromagnetic energy-momentum tensor T used in general relativity. If you divide the total charge and current into their associated particles, you get the Lorentz force density. This, in turn, can explain the torque.

What does force mean and its formula

The Lorentz force is usually called the force that affects an electron that is moving and located in a magnetic field. We are talking about a combination of two forces - magnetic, electric, concentrated on a charge. The Lorentz force is determined by the following values:

induction;
amount of charge;
the speed of movement of the particle.

The direction of the charged particle is orthogonal to the plane where the velocity vectors are located. For the Lorentz force in physics, there is a resultant force - this is the Ampere force.

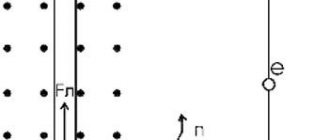
To clearly demonstrate the required force, let's remember the experiment that you were probably shown in physics class - with a magnet, metal filings, a sheet of paper. The teacher brought a magnet to the sawdust from below, through the paper, and they lined up in clear lines. They form the force field of the magnet. It is noteworthy that this is a closed space without beginning or end. We are talking about a vector quantity that, under any circumstances, rushes towards the north pole of the magnet. If a charged particle enters the field, the trajectory changes. The angle of deflection is determined by the speed of the particle, as well as the force that affects the electron. This is the desired Lorentz force; to calculate it, use the formula: FL=qVB, here:

q – charge strength (indicated in Coulombs);
V – speed of charge movement (indicated in m/s);
B - field induction (denoted in Tesla).

The definition of strength, as well as the formula, proposed at the end of the 19th century, are still relevant today.

Direction of force

The indication of the Lorentz force becomes the opposite if two conditions are met:

when the sign of the charge also becomes opposite;
the directions of other vectors remain unchanged.

The trajectory of an electron is usually called a helical line.

When does it occur

The magnetic field parameters remain unchanged if the charged particle is stationary. Similarly, the conductor is not affected by the Ampere force when there is no current.

To determine the Lorentz force modulus, the following conditions will need to be met:

1. the presence of a charge on the particle;

2. presence of a magnetic field;

3. the particle must move.

If one of the three conditions is not met, there is no power.

Concept of electric field strength

The electromagnetic field actually consists of two halves - electric and magnetic. They are like twins, with everything the same, but with different personalities. And if you look closely, you can notice slight differences in appearance.

The same goes for force fields. The electric field also has intensity - a vector quantity, which is a force characteristic. It affects the particles that are motionless in it. In itself, it is not a Lorentz force; it simply needs to be taken into account when calculating the effect on a particle in the presence of electric and magnetic fields.

Electromagnetic induction, magnetic flux

The term magnetic induction refers to the physical property of a magnetic field. This quantity is vector, and the symbol B is used to denote it. Induction characterizes the force affecting a charged particle that moves in a magnetic field. It is important to remember that the force, as well as the direction of motion of the electron, are perpendicular to each other.

Induction occurs when a magnet moves in a coil and a current is produced. Consequently, the magnetic flux increases proportionally.

Induction is explained as follows: the metal structure of the coil is crystalline, electrical charges are located here. If there is no influence of the magnet on the coil, these charges do not move. When it enters a magnetic field, a charge speed is created as the electrons begin to move. A current is formed in the conductor, its strength is determined by the parameters of the magnet and conductor.

Good to know! If a conductor is surrounded by a magnetic field, the electrons are shifted at a certain angle and are placed parallel to the lines of force.

Wide Application

The first instruments for the proposed discoveries were cyclotrons. The meaning of their work is quite simple: the particles move in a semicircle. Every time they pass a certain area, a special module turns on an electric field to speed them up.

Mass spectrometers are used to identify atoms and molecules. They are used in the following devices:

electric motors;
loudspeakers;
rail guns.

The ability of the Lorentz force to couple mechanical displacement to electrical current is of great interest in medical acoustics. For example, a hydrophone was being developed to map the velocity of particles in an acoustic field. It was supposed to be built using thin copper wire and an external magnetic field.

The model was developed to determine the relationship between acoustic pressure and the measured electrical current that is induced when a wire vibrates in the acoustic field of an ultrasonic transducer.

The created prototype was characterized. Its spatial resolution, frequency response, sensitivity, reliability and directivity characteristics were investigated. An imaging technique called electrical impedance tomography has also been studied. In this method, biological tissue is vibrated with ultrasound in a magnetic field, which induces an electric current. This method was applied to image a gelatin phantom, a beef muscle sample, and a thermal lesion in a chicken breast sample. This showed that the technique could be useful in providing additional contrast compared to conventional ultrasound imaging.

Law of Electromagnetic Induction

In simple words, one of the basic laws of physics can be formulated as follows: changes in the magnetic field, provided that it crosses the contour, are accompanied by the appearance of an electromotive force. It is proportional to the rate of change of the magnetic field. It doesn’t matter what provoked such changes in the magnetic field.

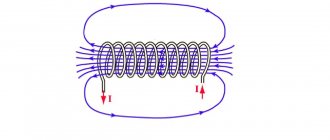
The law was proposed by Michael Faraday at the beginning of the 19th century. It is on Faraday's law that the work of transformers, generators, and chokes is based. The circuit is a coil of wire, the magnetic field forms a magnet. To measure the electromotive force, the wire is connected to a voltmeter.

Let's consider two options:

the magnet is stationary above the coil - a constant field is formed, the parameters of which do not change, and accordingly, the electromotive force does not arise;
the position of the magnet changes - any movement of the magnet causes changes in the field, this is the source of the appearance of electromotive force and voltage, EMF measurements can be carried out while the magnet is moving.

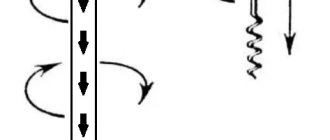
The EMF in the circuit generates a current, its orientation is determined using Lenz's rule, formulated as follows - the current that appears during changes in the magnetic field passing through any circuit restrains these changes. Thus, when a magnet acts on the coil, the following happens - the magnetic flux increases, a current and a magnetic field appear, which prevents the increase in the magnet's field.

Good to know! To understand where the current is moving, you need to screw the gimlet in the direction of the north pole; a magnetic field is formed in a similar direction. This means that the current flows parallel to the clockwise direction.

If the magnet does not act on the coil, the following happens - the magnetic flux decreases, accordingly, the magnetic field of the current restrains the decrease in the magnet's field. To determine in which direction the current is moving, the gimlet is unscrewed, its movement indicates where the current is directed, namely, in the opposite direction from the clockwise direction.

Chaos theory

Is it possible to predict the chaotic movement of the elements of any system? What does chaotic dynamics depend on? Could the flapping of a butterfly's wing finally cause a tornado? Some important answers to these and other questions were found by American meteorologist Edward Lorenz, the (unwitting) coiner of the term “butterfly effect” and creator of the “strange attractor.” We talk about this in the first material devoted to the most interesting differential equations.

In 1972, Edward Lorenz, a professor of meteorology at the Massachusetts Institute of Technology, was planning to speak at a conference, but in the heat of work, he did not have time to submit the topic of his lecture. The organizer, rushing to send out invitations, chose the headline for him: “Predictability: Can the flapping of a butterfly's wing in Brazil cause a tornado in Texas?” This is how the term “butterfly effect”, known today throughout the world, appeared.

Edward Lorenz was born in 1917 in a small town in Connecticut. He decided to study atmospheric phenomena as a child, having experienced the shock of how easily sunny weather could give way to a storm with thunder and lightning.

The path to fulfilling the dream was long: a master's degree at Harvard, work as a meteorologist in the aviation division of the US Army, defense of a dissertation in the post-war period, and finally a position as a research assistant and, later, a professor at MIT.

In his speech, Lorenz highlighted several key ideas:

⦁ If the flapping of a butterfly’s wing can cause a tornado, then all previous and future flapping can do the same, as well as the flapping of the other millions of butterflies, not to mention the activity of the countless population of our planet.

⦁ If the flapping of a butterfly's wing can cause a tornado, then the same flapping can equally prevent one.

The flapping of a butterfly's wing in this context should be perceived as a small change in the initial conditions of the system under study, which can both cause a tornado and change its trajectory or even cause its attenuation.

Unlike the domino effect, where a specific (usually minor) action leads to a specific (usually significant) result in an unambiguous manner, the swing of a butterfly may have no effect on the behavior of the tornado.

Lorentz system

Lorentz studied convection (heat exchange resulting from the movement of liquid or gas molecules) in the Earth's atmosphere. To describe such physical processes, a model is often used that includes the Navier-Stokes equations, which describe the motion of a viscous Newtonian fluid (with the exception of some special cases, their solutions in general form are currently unknown):

⦁ Equation of motion in vector form:

⦁ Thermal conductivity equation describing the distribution of temperature in space over time:

⦁ The continuity equation, which, at its core, describes the principle of conservation of mass of something:

In the original, these three components give the following system:

We will not go into a detailed explanation of all of the above. It is enough just to understand that this is a rather complex model, and Lorentz, as a result of many pages of calculations, managed to construct a simplification of it:

Here, a variable with a dot on top means its time derivative. In details:

x is responsible for the intensity of convection;
y displays the difference between the incoming and downstream temperatures;
z characterizes the deviation of the vertical temperature profile from the linear dependence;
σ > 1—Prandtl number (a criterion for the similarity of thermal processes in liquids and gases);
ρ > 0—Rayleigh number (reflects the behavior of a liquid under the influence of a temperature gradient);
β > 0 is a number reflecting the geometry of the convective cell.

Using this system of equations, it is possible to calculate how a fluid medium will behave if it is uniformly heated from below and cooled from above. Just as it happens with air flows in the atmosphere. In particular, it allows you to understand what result even a small change in the initial parameters will lead to.

Chaotic movement

Before proceeding with the direct analysis of the resulting system, we will consider some combinations of trajectories. For clarity, we will use the same parameter values as Lorentz himself: σ = 10, ρ = 28, β = 8/3.

Let us depict the movement of two points, the distance between which is initially small:

⦁ P0 = (0, 1, 1) ⦁ P1 = (0, 1, 1.01)

Quite an interesting result! At first, the trajectories are almost indistinguishable, then they deviate very slightly, after which the difference becomes significant.

Let's try again, but now let's take points at a considerable distance from each other:

⦁ P0 = (−25, 20, −15) ⦁ P1 = (−15, 40, 15)

Even despite such a difference in initial conditions, the trajectories end up on a figure that they subsequently do not leave. It’s very strange, it’s as if something attracts them...

Lorentz strange attractor

Indeed, this figure is called a strange Lorentz attractor (from the English attract

- “to attract”).

The formal mathematical definition is that an attractor is a subset of phase space such that all trajectories starting not too far from it tend towards it over time. (This is one possible definition of the concept of an attractor; there are others that are not equivalent to this one.)

The word “strange” here appears in this way: the attractor as a set cannot be represented in the form of a curve or surface; it has a more complex, fractal structure. The attractor trajectories do not close, and small deviations constantly accumulate, exponentially.

The above can be illustrated as follows: two trajectories released from close points eventually diverge quite far. Moreover, in order to delay the moment of acceleration, for example, by one second, you need to reduce the distance between the starting points, say, by half. And for two seconds - four times. And by three - eight times, and so on.

This means that, even using a powerful computer, we cannot calculate the trajectory passing near the attractor with reasonable accuracy over a long period of time. At each step of calculations, errors are inevitably introduced (due to rounding of numbers and errors in numerical methods), which quickly accumulate and lead to the fact that the found trajectory is very different from the real one.

This distortion cannot be corrected simply by increasing the computer's power. This phenomenon is called “dynamic chaos”.

Below is a strange attractor model that you can experiment with by changing the input values. For those who want to study the mathematical side in more detail, there is one more section immediately after the model.

You can rotate the model or zoom in/out (using the mouse buttons on a desktop or your fingers on a smartphone screen). The meaning of the sliders from top to bottom:

parameter value σ;
the value of the parameter ρ;
β parameter value;
trajectory density.

Orange spheres are points moving according to the Lorentz system. Accordingly, the blue lines are the trajectories of these points.

A little math

The Lorentz system has several remarkable properties:

⦁ The right side of the system has no free members, that is, it is homogeneous.

⦁ If the triple (x, y, z) is a solution, then (-x, -y, z) is also suitable - the system has symmetry.

⦁ All trajectories of the system are limited by a certain limit set due to the negative divergence of the vector field:

In other words, the flow compresses the volume of phase space - this is called a dissipative system.

The Lorentz system has equilibrium points, and one of them is obvious - E0 = (0, 0, 0). Let's try to find others:

Assuming that x ≠ 0 (otherwise the solution will be (0, 0, 0)) and ρ ≥ 1, we obtain:

Thus, we got two more equilibrium points for x ≠ 0, ρ ≥ 1:

We examine these points for stability using the Jacobian:

Let's start from the point E0 = (0, 0, 0):

The radical expression is greater than zero, so all eigenvalues are real.

for ρ < 1, the roots are negative – a stable node;
for ρ = 1 there is a zero root - a bifurcation point;
for ρ > 1 there is a positive root—an unstable saddle.

For the remaining two points, we will not delve into the calculations in detail in order to maintain simplicity of perception.

It turns out that they are either simultaneously stable or simultaneously unstable. Asymptotic stability occurs when one of the following conditions is true:

Chaos by definition

Determinism was often equated with predictability, but Lorenz was able to show that determinism can only give a short-term prediction of the behavior of a system, while in the long term the consequences can be unpredictable. This is what the term “chaos” means.

However, one should not confuse chaos with chaos - the Lorentz attractor is a vivid example of this, because all trajectories are limited in one way or another and do not leave a certain set.

What about the weather? Lorenz's work led to improvements in the systems used to make her forecasts:

weather stations began to collect significantly more data;
for calculations in model simulations, methods began to be used to achieve greater accuracy;
Experimental meteorologists have realized the importance of a system's sensitivity to initial conditions—they run a large number of simulations whose input data differs only slightly, so that the phenomenon that occurs in most cases is "recognized" as the most likely.

Practice words: what prevents you from predicting the weather a month in advance?

Theoretically, it is possible to forecast the weather day by day in detail for two weeks, but practically, at the current level of scientific development, for 5-7 days.
I can, of course, repeat the favorite mantras of meteorologists: the atmosphere is a chaotic system with well-defined dissipation and the like. In fact, a weather forecast... is a solution to a system of differential equations. The accuracy of the result, that is, the accuracy of solving these equations, depends on the initial data. So, according to the modern understanding of the fundamental laws of nature, the theoretical minimum error of the initial data leads to the fact that after two weeks the solution to the problem ceases to depend on these very initial data. In other words, no matter how hard we try, it is no longer possible to predict the situation more than two weeks in advance. Alas! And this is such a difficult philosophical situation, which was first realized by meteorologists: no matter how much science develops, two weeks is a threshold, and beyond this threshold it is impossible to predict day by day.

From an interview with Roman Vilfand, scientific director of the Hydrometeorological Center of Russia

Despite the apparent simplicity of the system of the same name, Lorentz managed to change the views of many mathematicians and physicists on things familiar to them and became the founder of a new branch of chaos theory.

Lev Khoroshansky

Literature

Lorenz, E.
Predictability: Does the Flap of a Butterfly's Wings in Brazil Set off a Tornado in Texas?
1972. Ghys, E.
The Lorenz Attractor, a Paradigm for Chaos. 2010.

Knill, O.

The Lorenz System. 2005.

Semenova, E.

Chaotic behavior of dynamical systems. 2014.

Current magnetic field energy

The parameter indicates how much work is done by the current in the conductor to form a magnetic field. The value is directly determined by the inductance of the conductor around which the field is formed.

To calculate the energy, there is a formula equal to the product of the circuit inductance, the current squared, the resulting result is divided by two: W = LI2/2.

Movement of a particle in a magnetic field

For clarity, let's consider several options. The direction of the particle is perpendicular to the field; it moves in a circle, the radius of which is constant.

The Lorentz force is directed radially towards the central point of the circle, and radial acceleration appears. If we apply Newton's second law, we obtain the following equation: Fl = maT = mv2/R. From this equation we obtain the following: mv2/R = qvB. Using this expression, we can derive a formula for calculating the angular velocity of the electron: w = v/R = qB/m.

If in this expression the values q, m, B are unchanged, the angular velocity also remains unchanged. The radius of movement is affected only by speed.

The Lorentz force forms acceleration and is directed into the circle. The direction of the positively charged particle and the screw are the same, but the orientation of the screw and the magnetic field are opposite. Accordingly, the negatively charged particle rotates in the opposite direction.

The Lorentz force is zero provided that the motion of the particle and the induction vector are parallel. The electron moves uniformly and in a straight line.

The third option is that the electron moves in the field, the velocity vector forms an angle with the magnetic field. Speed is broken down into the following components:

directed along the field – v = vcos0;
directed perpendicular to the field – v = vsin0.

To determine the motion of a particle, you need to calculate the sum of two motions - parallel to the magnetic field (vcos0), rotation in a circle (w = qB/m). To summarize, the particle moves in a spiral.

The effect of a magnetic field on a moving charge

- the force acting from the magnetic field on a moving electrically charged particle.
where q is the particle charge;

V—charge speed;

B—magnetic field induction;

a is the angle between the charge velocity vector and the magnetic induction vector.

The direction of the Lorentz force is determined by the left-hand rule:

If you place your left hand so that the component of the induction vector perpendicular to the speed enters the palm, and the four fingers are located in the direction of the speed of movement of the positive charge (or against the direction of the speed of the negative charge), then the bent thumb will indicate the direction of the Lorentz force:

Since the Lorentz force is always perpendicular to the speed of the charge, it does not do work (that is, it does not change the value of the charge speed and its kinetic energy).

If a charged particle moves parallel to the magnetic field lines, then Fl = 0, and the charge in the magnetic field moves uniformly and rectilinearly.

If a charged particle moves perpendicular to the magnetic field lines, then the Lorentz force is centripetal:

and creates a centripetal acceleration equal to:

In this case, the particle moves in a circle.

According to Newton's second law: the Lorentz force is equal to the product of the particle mass and the centripetal acceleration:

then the radius of the circle:

and the period of charge revolution in a magnetic field:

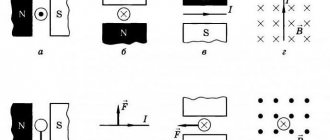
Since electric current represents the ordered movement of charges, the effect of a magnetic field on a conductor carrying current is the result of its action on individual moving charges. If we introduce a current-carrying conductor into a magnetic field (Fig. 96a), we will see that as a result of the addition of the magnetic fields of the magnet and the conductor, the resulting magnetic field will increase on one side of the conductor (in the drawing above) and the magnetic field will weaken on the other side conductor (in the drawing below). As a result of the action of two magnetic fields, the magnetic lines will bend and, trying to contract, they will push the conductor down (Fig. 96, b).

The direction of the force acting on a current-carrying conductor in a magnetic field can be determined by the “left-hand rule.” If the left hand is placed in a magnetic field so that the magnetic lines coming out of the north pole seem to enter the palm, and the four extended fingers coincide with the direction of the current in the conductor, then the large bent finger of the hand will show the direction of the force. Ampere force acting on an element of the length of the conductor depends on: the magnitude of the magnetic induction B, the magnitude of the current in the conductor I, the element of the length of the conductor and the sine of the angle a between the direction of the element of the length of the conductor and the direction of the magnetic field.

This dependence can be expressed by the formula:

For a straight conductor of finite length, placed perpendicular to the direction of a uniform magnetic field, the force acting on the conductor will be equal to:

From the last formula we determine the dimension of magnetic induction.

Since the dimension of force is:

i.e., the dimension of induction is the same as what we obtained from Biot and Savart’s law.

Tesla (unit of magnetic induction)

Tesla, a unit of magnetic induction in the International System of Units, equal to the magnetic induction at which the magnetic flux through a cross section of 1 m2 is equal to 1 weber. Named after Tesla. Designations: Russian tl, international T. 1 tl = 104 gs (gauss).

Magnetic moment , magnetic dipole moment is the main quantity characterizing the magnetic properties of a substance. The magnetic moment is measured in A⋅m2 or J/T (SI), or erg/Gs (SGS), 1 erg/Gs = 10-3 J/T. The specific unit of elementary magnetic moment is the Bohr magneton. In the case of a flat circuit with electric current, the magnetic moment is calculated as

where is the current strength in the circuit, is the area of the circuit, is the unit vector of the normal to the plane of the circuit. The direction of the magnetic moment is usually found according to the gimlet rule: if you rotate the handle of the gimlet in the direction of the current, then the direction of the magnetic moment will coincide with the direction of the translational movement of the gimlet.

For an arbitrary closed loop, the magnetic moment is found from:

where is the radius vector drawn from the origin to the contour length element

In the general case of arbitrary current distribution in a medium:

where is the current density in the volume element.

So, a torque acts on a current-carrying circuit in a magnetic field. The contour is oriented at a given point in the field in only one way. Let's take the positive direction of the normal to be the direction of the magnetic field at a given point. The torque is directly proportional to the magnitude of the current I, the area of the circuit S and the sine of the angle between the direction of the magnetic field and the normal.

here M is the torque , or moment of force , and is the magnetic moment of the circuit (similarly, the electric moment of the dipole).

In a non-uniform field ( ), the formula is valid if the size of the contour is small enough (then the field within the contour can be considered approximately homogeneous). Consequently, the circuit with current still tends to turn around so that its magnetic moment is directed along the lines of the vector.

But, in addition, a resultant force acts on the circuit (in the case of a uniform field and . This force acts on a circuit with a current or on a permanent magnet with a moment and draws them into an area of a stronger magnetic field. The work of moving a circuit with a current in a magnetic field.

It is easy to prove that the work done to move a circuit with current in a magnetic field is equal to , where and are the magnetic fluxes through the area of the circuit in the final and initial positions. This formula is valid if the current in the circuit is constant , i.e. When moving the circuit, the phenomenon of electromagnetic induction is not taken into account.

The formula is also valid for large circuits in a highly inhomogeneous magnetic field (provided I=const).

Finally, if the circuit with current is not displaced, but the magnetic field is changed, i.e. change the magnetic flux through the surface covered by the circuit from value to then for this you need to do the same work. This work is called the work of changing the magnetic flux associated with the circuit. The flux of the magnetic induction vector (magnetic flux) through the area dS is a scalar physical quantity that is equal to

(1)

where Bn=Bcosα is the projection of vector B onto the direction of the normal to the site dS (α is the angle between vectors n and B ), d S = dS n is a vector whose module is equal to dS, and its direction coincides with the direction of the normal n to the site. The flux of vector B can be either positive or negative depending on the sign of cosα (set by choosing the positive direction of the normal n ). The flux of vector B is usually associated with the circuit through which the current flows. In this case, we specified the positive direction of the normal to the contour: it is associated with the current by the rule of the right screw. This means that the magnetic flux that is created by the circuit through the surface limited by itself is always positive.

The flux of the magnetic induction vector ФB through an arbitrary given surface S is equal to

(2)

For a uniform field and a flat surface, which is located perpendicular to the vector B , Bn=B=const and

This formula gives the unit of magnetic flux Weber (Wb): 1 Wb is the magnetic flux that passes through a flat surface with an area of 1 m2, which is located perpendicular to a uniform magnetic field and whose induction is 1 T (1 Wb = 1 T•m2).

Gauss's theorem for field B : the flux of the magnetic induction vector through any closed surface is zero:

(3)

This theorem is a reflection of the fact that there are no magnetic charges, as a result of which the magnetic induction lines have neither beginning nor end and are closed.

Consequently, for the flows of vectors B and E through a closed surface in the vortex and potential fields, different formulas are obtained.

As an example, let's find the flow of vector B through the solenoid. The magnetic induction of a uniform field inside a solenoid with a core with magnetic permeability μ is equal to

The magnetic flux through one turn of the solenoid with area S is equal to

and the total magnetic flux, which is linked to all turns of the solenoid and is called flux linkage ,

Left hand rule for Lorentz force

Do you want to know where the Lorentz force is directed? Use the left hand rule. The essence of this rule is this: the open left palm is placed perpendicularly, at the same time parallel to the lines of the field. Then four indicates the movement of current, the thumb bent 90 degrees demonstrates the Lorentz force.

There is another method to determine the orientation of the Lorentz force vector using the left-hand rule in physics. The thumb, index, and middle fingers are positioned at an angle of 90 degrees. We will get the following:

the middle one demonstrates the movement of current;
index – magnetic field;
large – Lorentz force.

Let's look at the rule using a specific example. For example, an electron moves towards a person. Accordingly, on the right is the north pole, on the left is the south pole. This formulation is correct for the proton. Since the electron is negatively charged, the four fingers of the right hand are extended towards the movement of the proton - forward. The magnetic field is formed towards the south pole. Place your left palm edgewise, then the field lines pass through the palm, four fingers look forward, and the thumb, bent 90 degrees, demonstrates the vector indication of the Lorentz force - from bottom to top.

Right hand rule

Before understanding the right-hand rule, it is necessary to understand that any force and Lorentz force is no exception - a vector, which means that this parameter has two meanings - magnitude and indication. If you know the orientation of the factors, determining the direction of the cross product is not difficult. This will require a left or right hand rule. This rule is known as the gimlet or screw rule. It applies not only to determining the direction of the Lorentz force vector, but also to determining the orientation of any other vector products.

For a better understanding of the rules:

ions with a negative charge, as well as electrons, are always directed from the cathode to the anode;
ions with a positive charge, as well as protons, are directed from the anode to the cathode;
electric current moves in a direction that is opposite to the direction of electrons.

To determine the orientation of the desired Lorentz force, you will need to place your right palm so that the palm and the direction of the current are directed parallel. In this case, rotating the gimlet, or in this particular example the thumb, will indicate the direction of the induction vector.

To explain in simple words, you need to screw in the corkscrew with your right hand.

Important! The direction, as well as the angle at which a charged particle will deviate from its trajectory under the influence of a magnetic field, is determined by the charge of the particle.

Application of Lorentz force in technology

The Lorentz force is represented on the largest scale in the Earth's magnetic field. Our planet is a magnet. Accordingly, charged particles located at the north and south magnetic poles move in a spiral and collide with atoms that are located in the upper layers of the atmosphere. We have now described the mechanism for the appearance of the northern lights. However, there are other, special cases of application of the Lorentz force.

Electric generator

When scientists proved that a conductor carrying current is affected by a magnetic field, they decided to use this discovery in order to make a conductor located in a magnetic field move. Thus, magnetism was transformed into mechanical movement, and accordingly, an engine was created.

A simplified model of the mechanism consists of a stator (a stationary part and fixed magnets), inside of which a rotor (a frame made of a conductor material) rotates. To supply current to the frame, it is connected to the terminals via contacts. Now the motor model is connected to a source of electricity, as a result the frame rotates.

Important! In engines, as well as generators, it is the Lorentz force that causes the rotor to move under the influence of the electromagnetic field, the stator.

Spectrograph

The operating principle of the device is as follows: the source of charged particles is placed in a vacuum chamber, thus eliminating the possibility of air acting on charged particles. An electric field is artificially formed inside the device, under the influence of which particles with a charge are accelerated, pass along an arc and hit the photographic plate, leaving characteristic marks on it. The radius of the trajectory varies depending on the specific charge. The radius can be measured and then the mass of the charged particle can be calculated.

Interesting fact! Spectrographs are used to study the composition of soil from the Moon.

Kinescope

Until recently, every TV was equipped with a picture tube, and in the absence of the Lorentz force, the equipment would not work. Let's consider the principle of operation of a kinescope - it is a vacuum cylinder, inside of which there is a source of electrons. The coils form a magnetic field, which controls the electron beam. The screen is coated with a special substance that glows when electrons act on it. The trajectory of electrons is controlled by a magnetic field, and the speed is controlled by an electric field. Thus, if you direct charged particles to specific points on the screen, it will glow in accordance with the image.

Good to know! Bring a magnet close to the screen, and you will see how the image will be distorted, as the trajectory of charged particles will change, because the magnetic field of the magnet will begin to act on them.

Cyclothorone

This device uses the dependence of the rotation frequency of a particle with a charge on the speed of movement in a magnetic field. The main area of application of the cyclotron is the acceleration of particles to maximum speeds.

The device consists of two half-cylinders, hollow inside, visually resembling the letter D. They are installed with straight edges to each other and placed in a magnetic field. An electric field appears between the faces; its frequency is similar to the frequency of rotation of charged particles. In one period of rotation, each particle is twice affected by the electric field, while the speed of movement increases and at a certain moment, when the speed reaches its maximum, the particle flies out through the hole.