Problems on the topic “Lorentz force”
Even if you are not a beginner, before solving problems, read the general instructions and keep useful formulas on hand just in case.
Lorentz force problem No. 1
Condition
An electron with an energy of 300 eV moves perpendicular to the induction lines of a uniform magnetic field with a strength of 465 A/m. Determine the Lorentz force, speed and radius of the electron trajectory.
Solution
The electron speed can be found from the kinetic energy formula:
E k = m v 2 2 v = 2 E k m
The Lorentz force is a centripetal force, which means that according to Newton’s second law, we can write:
Magnetic induction is equal to the intensity multiplied by the magnetic constant. Substituting the previously found expression for speed into the formula for radius and Lorentz force, we write:
R = m 2 E kt q μ 0 H = 2 E kt q μ 0 HF l = q 2 E kt μ 0 H
Now all that remains is to substitute the values and calculate:
v = 2 4, 8 10 - 16 9, 1 10 - 31 = 3, 25 10 7 m s F l = 4 3, 14 10 - 7 465 1, 6 10 - 19 3, 25 10 7 = 3 10 - 15 N R = 2 4, 8 10 - 16 9, 1 10 - 31 4 3, 14 10 - 7 465 1, 6 10 - 19 = 0.32 m
Answer: v = 3.25 · 10 7 m s; F l = 3 10 - 15 N; R = 0.32 m .
Lorentz force problem No. 2
Condition
An alpha particle flies into a magnetic field with an induction of 1 Tesla perpendicular to the field lines. Find the angular momentum of the particle relative to the center of the circle along which it will move.
Solution
When a particle flies into the field perpendicular to the lines of force, the Lorentz force begins to act on it, which acts as a centripetal force. The radius of the circle along which the particle will move:
R = mv QB m = 6.65 10 - 27 kg - mass of alpha particles Q = 2 e = 3.2 10 - 19 K l - z a r i d a l f a c h a s t i c s
We find the angular momentum of the particle relative to the center of the circle using the formula:
L = mv R = m 2 v 2 QB = 6, 65 10 - 27 2 0, 35 10 7 2 3, 2 10 - 19 1 = 5, 42 10 - 21 kg m 2 s
Answer: 5, 42 10 - 21 k g m 2 s .
Lorentz force problem No. 3
Condition
In a uniform magnetic field with induction B = 0.5 T, a rod of length l = 20 cm rotates with a frequency n = 10 s-1. The axis of rotation is parallel to the induction lines and passes through one of the ends of the rod perpendicular to its axis. Determine the potential difference U at the ends of the rod.
Solution
Let us consider the physical essence of the processes taking place in the rod. When a rod moves in a magnetic field, an induced emf arises in it, which is caused by the action of the Lorentz force on the charges of the rod.
Under the influence of this force, a separation of charges occurs in the rod: free electrons move upward and a potential difference arises between the ends of the rod.
The charges at the ends of the rod create a field E, which prevents further separation of charges. At some point, the Lorentz force will be balanced with the force of the emerging field:
F l = e E E = F l e = ev B e = v B
The speed of the lower end of the rod, and therefore the speed of the electrons in it, can be found by knowing the rotation frequency and the length of the rod:
v = 2 π n l
Taking this into account, the expressions for the electric field strength will be rewritten:
E = 2 π nl B
The induced potential difference, by definition, is equal to:
U = E l U = 2 π nl 2 B = 2 3.14 10 - 1 0.2 2 0.5 = 1.3 V
Answer: 1.3 V.
Lorentz force problem No. 4
Condition
What force acts on a charge of 0.005 C moving in a magnetic field with an induction of 0.5 T at a speed of 150 m/s at an angle of 45 degrees to the magnetic induction vector?
Solution
This is the simplest problem to determine the Lorentz force. Let us recall the formula and write that the Lorentz force acts on the charge, equal to:
F = q v B sin α
Let's substitute the values and calculate:
F = 0.005 150 0.5 2 2 = 0.26 N
Answer: 0.26 N.
Lorentz force problem No. 5
Condition
A body with a charge of 0.8 mC moving in a magnetic field is acted upon by a force equal to 32 N. What is the speed of the body if the magnetic field vector is perpendicular to it?
Solution
This is a classic problem using the Lorentz force formula. Since the velocity and magnetic induction vectors are perpendicular, we can write:
F = qv B sin α = qv B v = F q B = 32 0, 8 10 - 3 2 = 20 10 3 m s
Answer: 20000 m/s.
Are you undergoing magnetostatics? You may also be interested in:
- Problems on the Biot-Savart-Laplace law.
- Problems on the magnetic field circulation theorem.
Lorentz force 1
The article presents “initial” tasks: the simplest ones, in order to “try” the topic. You will find more advanced tasks in the same section.
Problem 1. A point charge Cl flies at a speed of m/s into a uniform magnetic field (Fig. 1). The charge velocity vector and the magnetic field induction vector are mutually perpendicular. Find the magnitude and direction of the force acting on the charge. Magnetic field induction T.
To task 1
Using the formula we calculate:
Answer: 0.1 mN
Problem 2. A point charge Cl flies at a speed of m/s into a uniform magnetic field. The charge is acted upon by a force H directed vertically upward (Fig. for problem 2). Determine the magnitude and direction of the magnetic field induction.
To task 2
Using the formula we calculate:
We determine the direction using the left hand: position the hand so that the thumb coincides with the force vector, and the remaining fingers coincide with the direction of flight of the particle. The magnetic induction vector would stick right into our palm if the particle were positively charged, but since the charge of the particle is negative, we will choose the opposite direction.
Answer: 1.25 Tesla, directed from the plane of the figure towards the observer.
Problem 3. A point charge K flies at a speed of m/s into a uniform magnetic field with induction T. The velocity and magnetic induction vectors make an angle (Fig. for Problem 3). Determine the magnitude and direction of the force acting on the charge.
To problem 3
Using the formula we calculate:
We determine the direction using the left hand: position the hand so that the fingers indicate the direction of flight of the particle (since it is positively charged). The magnetic induction vector should stick right into our palm. Since the particle is positively charged, we choose the direction that the thumb points.
Answer: 0.141 mN Problem 4. A proton moves at a speed of m/s perpendicular to a uniform magnetic field with induction T. Find the force acting on the proton and the radius of the circle along which it moves.
We determine the force using the formula:
Now let's determine the radius. The force is always directed perpendicular to the speed, therefore, it will “turn” the particle’s flight path into a circle. This force will be opposed by the force of inertia, the nature of which is centripetal force.
Then:
Answer: , see Problem 5. An electron describes a circle with a radius of mm in a magnetic field. Electron speed m/s. Find the magnetic field induction.
As in the previous problem, we equate the Lorentz force and the inertial force (centripetal):
Answer: 5 mT.
Lorentz force direction
The Lorentz force is perpendicular to the magnetic induction vector and the velocity vector of the moving charge. Its direction is determined using the left hand rule :
If the left hand is positioned so that the component of magnetic induction →B, perpendicular to the speed of the charge, enters the palm, and four fingers are directed along the movement of the positive charge (against the movement of the negative), then the thumb bent 90 degrees will show the direction of the Lorentz force acting on the charge .
Example No. 2. Proton p has a speed →v directed horizontally along a straight long conductor with current I (see figure). Where is the Lorentz force acting on the proton directed?
At the point where the proton is located, the magnetic induction vector is directed away from the observer. This follows from the gimlet rule. Now let's apply the left hand rule. To do this, let’s point the four fingers of our left hand in the direction of the proton’s movement—to the right. Let's turn the palm towards the observer so that the lines of magnetic induction enter it perpendicularly. Now let's move our thumb 90 degrees. He points up. Consequently, the Lorentz force acting on the proton is directed upward.
Solving problems in physics in grade 11 “Ampere's force. Lorentz force"
Examples of solving problems on the topics: “The power of Ampere. Lorentz force" 9th grade
Problem 1
Determine the force with which a uniform magnetic field acts on a conductor 20 cm long if the current in it is 300 mA, located at an angle of 45 degrees to the magnetic induction vector. Magnetic induction is 0.5 Tesla. Answer 0.021
Problem 2
A conductor with a current of 5 A is in a magnetic field with an induction of 10 Tesla. Determine the length of the conductor if a magnetic field acts on it with a force of 20 N and is perpendicular to the conductor.
Task 3
Determine the current strength in a conductor 20 cm long, located perpendicular to the magnetic field lines with an induction of 0.06 T, if a force of 0.48 N acts on it from the magnetic field.
Task 4
A conductor 20 cm long with a current strength of 50 A is in uniform magnetic field with an induction of 40 mT.
How much work will the current source do if the conductor moves 10 cm perpendicular to the magnetic induction vector (the magnetic induction vector is perpendicular to the direction of the current in the conductor). Problem 5
A conductor 0.15 m long is perpendicular to the magnetic induction vector of a uniform magnetic field, the modulus of which is B = 0.4 T.
The current strength in the conductor is 8 A. Find the work that was done when the conductor moved 0.025 m in the direction of the Ampere force. Problem 6
Determine the force acting on a charge of 0.005 C moving in a magnetic field with an induction of 0.3 Tesla at a speed of 200 m/s at an angle of 45 degrees to the magnetic induction vector.
Problem 7
What is the speed of a charged body moving in a magnetic field with an induction of 2 T if a force of 32 N acts on it from the magnetic field. The speed and the magnetic field are mutually perpendicular.
The body charge is 0.5 mC. Problem 8
Determine the centripetal force acting on a proton in a uniform magnetic field with an induction of 0.01 T (the magnetic induction vector is perpendicular to the velocity vector), if the radius of the circle along which it moves is 5 cm.
Problem 9
With what acceleration does an electron move in a uniform magnetic field (the magnetic induction vector is perpendicular to the velocity vector) with an induction of 0.05 T, if the Lorentz force acting on it is equal to 5 × 10-13 N. (Since the Lorentz force is both centripetal force, and the electron moves in a circle, the problem requires calculating the centripetal acceleration that the electron acquires as a result of the action of the centripetal force.)
Independent work on the topic “The Power of Ampere. Lorentz force"
Independent work on the topic “The Power of Ampere. Lorentz force"
Option 1.
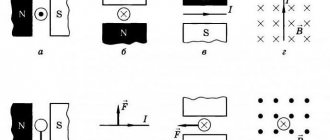
1. There is a conductor with current in a magnetic field (Fig. 25). What is the direction of the Ampere force acting on the conductor?
A.
From the reader.
B.
To the reader.
B.
Equal to zero.
2. A straight conductor 10 cm long is in a uniform magnetic field with an induction of 4 T and is located at an angle of 30° to the magnetic induction vector. What is the force acting on the conductor from the magnetic field if the current in the conductor is 3 A?
3. In a magnetic field with an induction of 5 T, an electron moves at a speed of 104 m/s, directed perpendicular to the magnetic field induction lines. What is the magnitude of the force acting on the electron from the magnetic field?
4. Figure 77 shows the cross-section of a conductor carrying current. The electric current is directed perpendicular to the plane of the drawing. In what case is the direction of the induction lines of the magnetic field created by this current correctly indicated?
1) Figure A 2) Figure B 3) There is no correct answer
5. In which direction is the proton deflected under the influence of a magnetic field (Fig. 29)?
A. To the left. B. Right. B. Up.
6. In all cases, determine the direction of the Ampere force.
A. To the left. B. Right. B. Up. G.
From the reader.
D.
To the reader.
E.
Equal to zero. G) down
7. In all cases, determine the direction of the Lorentz force
A. To the left. B. Right. B. Up. G.
From the reader.
D.
To the reader.
E.
Equal to zero. G) down
Independent work on the topic “The Power of Ampere. Lorentz force"
Option 2.
1. There is a conductor with current in a magnetic field (Fig. 28). What is the direction of the Ampere force acting on the conductor?
A.
From the reader.
B.
To the reader.
B.
Equal to zero.
2. A straight conductor 5 cm long is in a uniform magnetic field with an induction of 5 T and is located at an angle of 30° to the magnetic induction vector. What is the force acting on the conductor from the magnetic field if the current in the conductor is 2 A? Fig. No. 2
3. Determine the direction of the force. Rice. No. 2
A → B. ↓ C. ← D. ↑
4. In which direction is the electron deflected under the influence of a magnetic field (Fig. 30)?
A. To the left. B. Right. B. Up.
5. In a magnetic field with an induction of 5 T, an electron moves at a speed of 104 m/s, directed perpendicular to the magnetic field induction lines. What is the magnitude of the force acting on the electron from the magnetic field?
6. In all four options, determine the direction of the Ampere force
A. To the left. B. Right. B. Up. G.
From the reader.
D.
To the reader.
E.
Equal to zero. G) down
7. In all cases, determine the direction of the Lorentz force
A. To the left. B. Right. B. Up. G.
From the reader.
D.
To the reader.
E.
Equal to zero. G) down