Сторонние электрические силы. ЭДС. Закон Ома для полной цепи.

Разность потенциалов

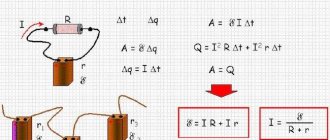
Напряжение на неоднородном участке цепи

(где есть сторонние силы) равно сумме ЭДС источника и разности потенциалов на этом участке:

Для однородного участка цепи

, где сторонние силы не действуют,

Т.е. напряжение совпадает с разностью потенциалов на концах участка цепи

.

Закон Ома для однородного участка
цепи в интегральной
и дифференциальной
форме
. Сопротивление и его зависимость от температуры. Сверхпроводимость.

Закон Ома для однородного участка
цепи в интегральной
и дифференциальной
форме
Закон Ома для однородного участка цепи: н

емецкий физик Георг Ом экспериментально установил, чтосила тока в цепи прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника:.

Закон Ома в дифференциальной форме (закон Ома для плотности тока).

Закон Ома в форме относится ко всему проводнику. Представим закон Ома в дифференциальной (т.е. относящейся к элементу тока длины
dl
) форме. Некоторая точка внутри проводника характеризуется вектором плотности тока , напряженностью электрического поляи свойствами материала проводника, т.е. удельным сопротивлением. Выделим мысленно малый объем вблизи рассматриваемой точки и подставимв закон Ома, получим:
,
здесь — разность потенциалов между сечениями
dS
отстоящими на расстоянии
dl
. Следовательно,.

Учтем, что — напряженность электростатического поля;- плотность электрического поля;- удельная электрическая проводимость.

Тогда из формулы (20) следует закон Ома в дифференциальной форме

: .

Электрические цепи. Электродвижущая сила

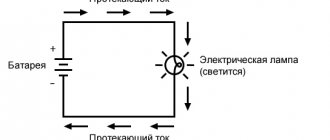
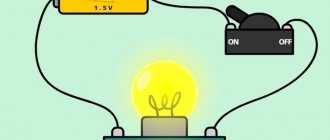
Электрическая цепь
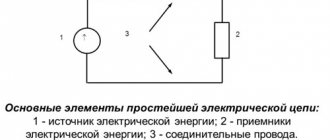
состоит из источника тока, потребителей электроэнергии, соединительных проводов и ключа, служащего для размыкания и замыкания цепи и других элементов (рис. 1).
Рис. 1
Рисунки, на которых изображены способы соединения электрических приборов в цепь, называются электрическими схемами

. Приборы на схемах обозначаются условными знаками.

Как отмечалось, для поддержания в цепи электрического тока необходимо, чтобы на концах ее (рис. 2) существовала постоянная разность потенциалов φ

A —
φ
B. Пусть в начальный момент времени
φ
A >
φ
B, тогда перенос положительного заряда
q
из точки
А
в точку
В
приведет к уменьшению разности потенциалов между ними. Для сохранения постоянной разности потенциалов необходимо перенести точно такой же заряд из
B
в
A
. Если в направлении
А
→
В
заряды движутся под действием сил электростатического поля, то в направлении
В
→
А
перемещение зарядов происходит против сил электростатического поля, т.е. под действием сил неэлектростатической природы, так называемых сторонних сил. Это условие выполняется в источнике тока, который поддерживает движение электрических зарядов. В большинстве источников тока движутся только электроны, в гальванических элементах — ионы обоих знаков.

Рис. 2

Источники электрического тока могут быть различны по своей конструкции, но в любом из них совершается работа по разделению положительно и отрицательно заряженных частиц. Разделение зарядов происходит под действием сторонних сил

. Сторонние силы действуют лишь внутри источника тока и могут быть обусловлены химическими процессами (аккумуляторы, гальванические элементы), действием света (фотоэлементы), изменяющимися магнитными полями (генераторы) и т.д.

Любой источник тока характеризуют электродвижущей силой — ЭДС.

Электродвижущей силой
ε
источника тока называют физическую скалярную величину, равную работе сторонних сил по перемещению единич ного положительного заряда вдоль замкнутой цепи
\(~\varepsilon = \frac{A_{stor}}{q} .\)
Единицей электродвижущей силы в СИ является вольт (В).

ЭДС является энергетической характеристикой источника тока.

В источнике тока в процессе работы по разделению заряженных частиц происходит превращение механической, световой, внутренней и т.п. энергии в электрическую. Разделенные частицы накапливаются на полюсах источника тока (места, к которым с помощью клемм или зажимов подсоединяют потребители). Один полюс источника тока заряжается положительно, другой — отрицательно. Между полюсами источника тока создается электростатическое поле. Если полюса источника тока соединить проводником, то в такой электрической цепи возникает электрический ток. При этом характер поля меняется, оно перестает быть электростатическим.

Рис. 3

На рисунке 3 схематично в виде сферического проводника изображена отрицательная клемма источника тока и сечение присоединенного к ней конца металлического провода. Пунктиром показаны некоторые линии напряженности поля клеммы до внесения в него провода, а стрелками — силы, действующие на свободные электроны провода, находящиеся в точках, помеченных цифрами. Электроны в различных точках поперечного сечения провода под действием кулоновских сил поля клеммы приобретают движение не только вдоль оси провода. Например, электрон, находящийся в точке 1

, оказывается вовлеченным в «токовое» движение. Но вблизи точек
2, 3, 4, 5
электроны имеют возможность скапливаться на поверхности провода. Причем поверхностное распределение электронов по длине провода не будет равномерным. Следовательно, подключение провода к клемме источника тока приведет к тому, что некоторые электроны начнут двигаться вдоль провода, а часть электронов будет скапливаться на поверхности. Неравномерное распределение электронов на его поверхности обеспечивает неэквипотенциальность этой поверхности, наличие составляющих напряженности электрического поля, направленных вдоль поверхности проводника. Это поле перераспределенных электронов самого проводника и обеспечивает упорядоченное движение других электронов. Если распределение электронов по поверхности проводника с течением времени не изменяется, то такое поле называют
стационарным электрическим полем
. Таким образом, главную роль в создании стационарного электрического поля играют заряды, находящиеся на полюсах источника тока. При замыкании электрической цепи взаимодействие именно этих зарядов со свободными зарядами проводника приводит к появлению на всей поверхности проводника нескомпенсированных поверхностных зарядов. Именно эти заряды создают стационарное электрическое поле внутри проводника по всей его длине. Это поле внутри проводника однородное, и линии напряженности направлены вдоль оси проводника (рис. 4). Процесс установления электрического поля вдоль проводника происходит со скоростью
c
≈ 3·108 м/с.

Рис. 4

Как и электростатическое поле, оно потенциально. Но между этими полями имеются существенные отличия:

1. электростатическое поле — поле неподвижных зарядов. Источником стационарного электрического поля являются движущиеся заряды, причем общее число зарядов и картина их распределения в данном пространстве с течением времени не изменяются;
2. электростатическое поле существует вне проводника. Напряженность электростатического поля всегда равна 0 внутри объема проводника, а в каждой точке внешней поверхности проводника направлена перпендикулярно к этой поверхности. Стационарное электрическое поле существует и вне и внутри проводника. Напряженность стационарного электрического поля не равна нулю внутри объема проводника, а на поверхности и внутри объема имеются составляющие напряженности, не перпендикулярные к поверхности проводника;
3. потенциалы разных точек проводника, по которому проходит постоянный ток, разные (поверхность и объем проводника не эквипотенциальны). Потенциалы всех точек поверхности проводника, находящегося в электростатическом поле, одинаковы (поверхность и объем проводника эквипотенциальны);
4. электростатическое поле не сопровождается появлением магнитного поля, а стационарное электрическое поле сопровождается его появлением и неразрывно с ним связано.

Природа сторонних сил

Природа сторонних сил может быть различной. Например, в аккумуляторе или гальваническом элементе эта сила возникает благодаря химическим реакциям на границе соприкосновения электродов с раствором электролита (см. § 2.12). В фотоэлементе эти силы возникают благодаря действию света на вещество. В генераторах электростанций сторонняя сила — это может быть сила, действующая со стороны магнитного поля на электроны в движущемся проводнике (подробнее об этом будет говориться в главе 4).

От электростатики к электрокинетике

Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.

Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.

Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.

Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.

Вам это будет интересно Принцип работы, назначение и сферы применения триггеров

Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:

• 1800 г. — создание Вольтой гальванической батареи;
• 1826 г. — Ом формулирует свой закон для полной цепи;
• 1831 г. — обнаружение электромагнитной индукции Фарадеем.

Генератор постоянного тока

Я понимаю, что некоторые из приведенных выше утверждений могут вызвать у читателей удивление (возможно, даже возмущение). Так как именно среди таких читателей я надеюсь найти единомышленников, то напомню нетерпеливым, что всё сказанное относится к генераторам постоянного тока. К индукционным процессам мы обратимся позднее.

Рассмотрим несколько подробнее работу сторонних сил в абстрактном идеальном генераторе постоянного тока. Природа сторонних сил в таком генераторе может быть любой (в этом — смысл определения абстрактный), но они должны обладать всеми перечисленными выше свойствами. Идеальным мы называем генератор, не имеющий внутреннего сопротивления. При перемещении заряженных частиц в таком генераторе тепловые потери отсутствуют.

Положим, на всем пути между электродами на частицу, несущую положительный электрический заряд q

, действует постоянная сторонняя сила
F*
(Рис. 1). Величина этой силы определяется её природой и не зависит от электрического заряда частицы. Такую силу можно условно представить как результат воздействия на частицу удельной силы
E*
— «напряженности» некоторого «поля сторонних сил», отнесённой к единице электрического заряда частицы:
(1)
Допустим, что в тот момент, когда включаются сторонние силы, генератор «разряжен». Под действием этих сил положительно заряженные частицы устремляются к положительному электроду генератора, а отрицательные частицы — к противоположному полюсу. По мере того, как на электродах накапливаются заряды противоположного знака, возрастает разность потенциалов на выходных клеммах генератора. Одновременно растет и внутреннее электрическое (потенциальное) поле Ei

, направленное против сторонних сил. Когда сила воздействия этого поля на единицу электрического заряда частицы достигает (по модулю) силы
F*
«стороннего поля» (
Fi = -F*
), наступает равновесие
Ei = —E*
, и направленное движение заряженных частиц прекращается. На клеммах генератора устанавливается разность потенциалов
Δφ = φ1 — φ2 = Э
, которая и определяет ЭДС генератора, максимально возможную при данном способе генерации. Численно она равна работе, затрачиваемой сторонними силами на перемещение единицы электрического заряда внутри генератора.

Если клеммы генератора замкнуть на нагрузку R

(см. пунктир на Рис. 1), по цепи потечет постоянный ток
I = Э/R
и движение заряженных частиц в генераторе возобновится. Такой (рабочий) режим работы электрогенератора является квазистационарным: поступающие на электрод заряды компенсируют их уход во внешнюю цепь. При этом количество зарядов на электродах (а, следовательно, — и разность потенциалов) остаётся неизменным. Со временем не изменяются значения
Э
,
Ei
, сохраняется динамическое равенство
Fi = -F*
, а заряженные частицы в объёме генератора движутся равномерно («по инерции»). Подчеркнём, что этот режим работы генератора, как и режим холостого хода (при разомкнутой внешней цепи) — стационарный.

В реальном генераторе внутреннее сопротивление r* > 0

. В рабочем режиме движение заряженных частиц в генераторе остаётся равномерным, но сторонние силы немного превышают силы электростатические — на величину сил сопротивления движению частиц внутри генератора. При этом разность потенциалов на внешней цепи (напряжение на клеммах генератора) оказывается меньше его ЭДС на величину
Ir*
— падение напряжения внутри генератора.

Следует заметить, однако, что «внутреннее сопротивление» r*

не является электрическим сопротивлением в том же смысле, что и внешнее сопротивление
R
. Дело в том, что «падение напряжения» внутри генератора — это энергетические потери источника сторонних сил. Оно лишь численно равно удельным (на единицу электрического заряда) диссипативным потерям «сторонней» энергии. Однако, поскольку силы, действующие на заряженную частицу, не воздействуют на её электрический заряд, тепловые потери не зависят от заряда частицы. Сопротивление
r*
— это лишь некоторое эффективное значение, характеризующее внутренние потери энергии источника сторонних сил.

Чтобы показать, что ток внутри генератора («сторонний» ток) и ток во внешней цепи (потенциальный ток) имеют разную природу, мы сравнили эффективное сопротивление источника тока r*

с внутренним сопротивлением этого же источника
r
при протекании через него обратного (потенциального) тока.

На Рис. 2 приведена принципиальная схема этих измерений. Падение напряжения U

на испытуемом источнике питания измерялось высокоомным вольтметром
V
, а ток в цепи — миллиамперметром
mA
. Нагрузкой служил магазин сопротивлений
R
.

В положении I переключателя П

измерялся прямой ток от источника питания. По показаниям приборов рассчитывалось эффективное сопротивление источника
r* = U/I
. Затем в положении II переключателя навстречу ЭДС
Э
источника включалась ЭДС
Э1 > Э
. Измерялся обратный ток
I1
, по величине которого и падению напряжения
U1
на источнике рассчитывалось истинное («электрическое») сопротивление источника
r
. ЭДС источника измерялась непосредственно перед этим измерением и после него и учитывалась в расчетах.

Измерения проводились на 1,5-вольтовых батарейках для карманного фонарика. На Рис. 3 приведены результаты измерений эффективного «прямого» сопротивления r*

(пунктирная кривая) и истинного «обратного»
r
(контурная кривая) внутреннего сопротивления для трех батареек разного производства.

Изучение стабильности внутреннего сопротивления источников, формы этих зависимостей и прочие вопросы оставим специалистам-физхимикам (электрохимикам). Но приведенные экспериментальные результаты убедительно показывают, что природа прямого («стороннего») и обратного («потенциального») токов в электрохимических генераторах различна.