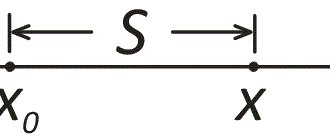The number of repetitions of any events or their occurrence in one timer unit is called frequency. This physical quantity is measured in hertz – Hz (Hz). It is denoted by the letters ν, f, F, and is the ratio of the number of repeating events to the period of time during which they occurred.
When an object rotates around its center, we can talk about such a physical quantity as rotation frequency, the formula:
Where:
- N – number of revolutions around an axis or in a circle,
- t is the time during which they were completed.
In the SI system it is denoted as – s-1 (s-1) and is referred to as revolutions per second (rps). Other units of rotation are also used. When describing the rotation of planets around the Sun, they speak of revolutions in hours. Jupiter rotates once every 9.92 hours, while the Earth and Moon rotate every 24 hours.
Rated rotation speed
Before defining this concept, it is necessary to determine what the nominal operating mode of a device is. This is the order of operation of the device in which the greatest efficiency and reliability of the process are achieved over a long period of time. Based on this, the nominal rotation speed is the number of revolutions per minute when operating in nominal mode. The time required for one revolution is 1/v seconds. It is called the rotation period T. This means that the relationship between the rotation period and frequency has the form:
For your information. The rotational speed of the asynchronous motor shaft is 3000 rpm, this is the rated rotation speed of the output shaft shank at the nominal operating mode of the electric motor.
How to find or find out the rotation frequencies of various mechanisms? For this, a device called a tachometer is used.
Angular velocity
When a body moves in a circle, not all its points move at the same speed relative to the axis of rotation. If we take the blades of an ordinary household fan that rotate around a shaft, then the point located closer to the shaft has a rotation speed greater than the marked point on the edge of the blade. This means they have different linear rotation speeds. At the same time, the angular velocity of all points is the same.
Angular velocity is the change in angle per unit time, not distance. It is denoted by the letter of the Greek alphabet – ω and has a unit of measure: radians per second (rad/s). In other words, angular velocity is a vector tied to the axis of rotation of the object.
The formula for calculating the relationship between rotation angle and time interval is:
Where:
- ω – angular velocity (rad/s);
- ∆ϕ – change in the angle of deflection when turning (rad.);
- ∆t – time spent on deviation (s).
The designation of angular velocity is used when studying the laws of rotation. It is used to describe the motion of all rotating bodies.
Angular velocity in specific cases
In practice, they rarely work with angular velocity values. It is needed in the design development of rotating mechanisms: gearboxes, gearboxes, etc.
You can calculate it using the formula. To do this, use the connection between angular velocity and rotational speed.
Where:
- π – number equal to 3.14;
- ν – rotation speed, (rpm).
As an example, the angular velocity and rotational speed of the wheel disk when moving a walk-behind tractor can be considered. It is often necessary to reduce or increase the speed of the mechanism. To do this, a device in the form of a gearbox is used, with the help of which the speed of rotation of the wheels is reduced. At a maximum speed of 10 km/h, the wheel makes about 60 rpm. After converting minutes to seconds, this value is 1 rpm. After substituting the data into the formula, the result will be:
Read also: Artifact Suite Parsley reviews
ω = 2*π*ν = 2*3.14*1 = 6.28 rad/s.
For your information. A reduction in angular velocity is often required in order to increase the torque or tractive effort of mechanisms.
How to determine angular velocity
The principle of determining angular velocity depends on how the circular motion occurs. If uniform, then the formula is used:
If not, then you will have to calculate the values of the instantaneous or average angular velocity.
The quantity we are talking about is a vector quantity, and Maxwell’s rule is used to determine its direction. In common parlance - the gimlet rule. The velocity vector has the same direction as the translational movement of a screw with a right-hand thread.
Let's look at an example of how to determine the angular velocity, knowing that the angle of rotation of a disk with a radius of 0.5 m varies according to the law ϕ = 6*t:
ω = ϕ / t = 6 * t / t = 6 s-1
The vector ω changes due to rotation in space of the rotation axis and when the value of the angular velocity modulus changes.
Speed of complex motion of a rigid body
Let's divide both parts of expression (1) by a time interval equal to $dt$, we get:
\[\overline{v}=\frac{d\overline{s}}{dt}=\frac{d{\overline{s}}_p}{dt}+\frac{d{\overline{s}} _v}{dt}={\overline{v}}_0+\overline{v'}\left(2\right),\]
where ${\overline{v}}_0$ is the speed of translational motion of points of a rigid body (equal for all points); $\overline{v'}$ - the speed caused by rotation varies for different points of the body.
The plane motion of a rigid body can be represented as the sum of two motions: translational with a speed of ${\overline{v}}_0$ and rotation with an angular speed of $\overline{\omega }$.
The linear speed $\overline{v'}$ of a point with a radius vector $\overline{r}$, which arises as a result of the rotation of the body (linear speed of rotation of the point), is equal to:
\[\overline{v'}=\left[\overline{\omega }\overline{r}\right]\left(3\right),\]
in expression (3) we mean the vector product. The linear rotation speed is found as:
\[v'=\omega r{\sin \alpha \ \left(4\right),\ }\]
where $\alpha $ is the angle between the direction of the angular velocity vector and the radius vector of the point (Fig. 1).
The speed of this point during complex movement is represented by the formula:
\[\overline{v}={\overline{v}}_0+\left[\overline{\omega }\overline{r}\right]\left(5\right).\]
There may be points in the body that participate in translational movement and rotation and at the same time remain motionless. Given ${\overline{v}}_0\ $ and $\overline{\omega }$, one can find a radius vector ($\overline{r}$) such that $\overline{v}=0.$
Rotation angle and period of revolution
Consider point A on an object rotating around its axis. When circulating over a certain period of time, it will change its position on the circle line by a certain angle. This is the rotation angle. It is measured in radians, because the unit is a segment of a circle equal to the radius. Another value for measuring the angle of rotation is a degree.
When, as a result of the rotation, point A returns to its original place, it means that it has completed a full rotation. If its movement is repeated n times, then we speak of a certain number of revolutions. Based on this, you can consider 1/2, 1/4 turn and so on. A striking practical example of this is the path that a cutter takes when milling a part fixed in the center of the machine spindle.
Attention! The rotation angle has a direction. It is negative when the rotation occurs clockwise and positive when it rotates counterclockwise.
If a body moves uniformly around a circle, we can talk about a constant angular velocity during movement, ω = const.
In this case, the following characteristics are used:
- period of revolution – T, this is the time required for a full revolution of a point in a circular motion;
- circulation frequency – ν, this is the total number of revolutions that a point makes along a circular path in a unit time interval.
Interesting. According to known data, Jupiter revolves around the Sun every 12 years. When the Earth makes almost 12 revolutions around the Sun during this time. The exact value of the round giant's orbital period is 11.86 Earth years.
Cyclic speed (reversal)
A scalar quantity that measures the frequency of rotational motion is called cyclic speed. This is the angular frequency, which is not equal to the angular velocity vector itself, but to its magnitude. It is also called radial or circular frequency.
Cyclic rotation frequency is the number of body revolutions in 2*π seconds.
For AC electric motors, this frequency is asynchronous. Their rotor speed lags behind the rotation speed of the stator magnetic field. The value that determines this lag is called slip - S. During the sliding process, the shaft rotates because an electric current arises in the rotor. Slip is permissible up to a certain value, exceeding which leads to overheating of the asynchronous machine, and its windings may burn out.
The design of this type of motor differs from the design of DC machines, where a current-carrying frame rotates in the field of permanent magnets. The armature contained a large number of frames, and many electromagnets formed the basis of the stator. In three-phase AC machines the opposite is true.
When an asynchronous motor operates, the stator has a rotating magnetic field. It always depends on the parameters:
- mains frequency;
- number of pole pairs.
The rotation speed of the rotor is in direct relation to the speed of the stator magnetic field. The field is created by three windings, which are located at an angle of 120 degrees relative to each other.
Read also: Replica caps for alloy wheels
How to change the engine speed?
You can change the speed of the rotating moment of the equipment mechanism in various ways, for example, mechanical gearboxes with gear shifts, clutches and other devices. But this is not always possible. In practice, 7 methods are used to correct the rotation speed of variable speed drives. All methods are divided into two main directions.
- Correction of the magnetic field by influencing the frequency of the current, reducing or increasing the number of pole pairs, voltage correction. The direction is typical for motors with a squirrel-cage (SC) rotor.
- Slip is corrected by supply voltage, adding another resistor to the rotor circuit circuit, installing dual supply, or using a cascade of valves. This direction is used for rotors with phases.
Adjusting frequency and voltage using a frequency converter, by creating an additional coil with switching poles of pairs, are the most popular methods.
Transition from angular to linear velocity
There is a difference between the linear velocity of a point and the angular velocity. When comparing the quantities in the expressions describing the rules of rotation, you can see the commonality between these two concepts. Any point B belonging to a circle with radius R makes a path equal to 2*π*R. At the same time, it makes one revolution. Considering that the time required for this is the period T, the modular value of the linear velocity of point B is found by the following action:
ν = 2*π*R / Т = 2*π*R* ν.
Since ω = 2*π*ν, it turns out:
Consequently, the linear speed of point B is greater, the further away the point is from the center of rotation.
For your information. If we consider cities at the latitude of St. Petersburg as such a point, their linear speed relative to the earth’s axis is 233 m/s. For objects on the equator – 465 m/s.
The numerical value of the acceleration vector of point B, moving uniformly, is expressed through R and angular velocity, thus:
a = ν2/ R, substituting here ν = ω* R, we get: a = ν2/ R = ω2* R.
This means that the larger the radius of the circle along which point B moves, the greater the value of its acceleration in absolute value. The farther a point of a rigid body is located from the axis of rotation, the greater the acceleration it has.
Therefore, it is possible to calculate accelerations, velocity modules of the required points of bodies and their positions at any time.
Understanding and ability to use calculations and not get confused in definitions will help in practice to calculate linear and angular velocities, as well as freely move from one quantity to another when making calculations.
Speed concept
When we compare the movement of any bodies, we say that some bodies move faster, while others move slower. We use such simple terminology in everyday life, talking, for example, about traffic. In physics, the speed of movement of bodies is characterized by a certain value. This quantity is called speed. General definition of speed (if the body is moving uniformly):
Velocity during uniform motion of a body is a physical quantity that shows how far the body has traveled per unit time.
By uniform motion of a body it is meant that the speed of the body is constant. The formula for finding speed: $v=frac$, $s$ is the path traveled by the body (that is, the length of the line), $t$ is the time (that is, the period of time during which the path was traveled).
According to the international SI system, the unit of linear speed is derived from two basic units - the meter and the second, that is, it is measured in meters per second (m/s). This means that the unit of speed is the speed of such uniform motion that a body travels a distance of one meter in one second.
Try asking your teachers for help
Speed is also often measured in km/h, km/s, cm/s.
Let's look at a simple example of a speed calculation problem.
Task. Moving uniformly, the train covers 219 km in 4 hours. Find its speed of movement.
Solution. $v=frac<219 km><4 h>=54.75frac<km><h>$. Let's convert kilometers into meters and hours into seconds: $54.75frac<km><h>=frac<54750 m><3600c>approx 15.2frac<m>$.
From the example we see that the numerical value of the speed differs depending on the selected unit of measurement.
In addition to the numerical value, speed has a direction. The numerical value of a quantity in physics is called the modulus. When a physical quantity also has a direction, then this quantity is called a vector quantity. That is, speed is a vector physical quantity.
In writing, the velocity module is denoted by $v$, and the velocity vector by $vec v$.
In turn, such quantities as path, time, length and others are characterized only by a numerical value. Then they say that these are scalar physical quantities.
Read also: Gas 3110 speedometer diagram
Ask a question to the experts and get an answer within 15 minutes!
In the case when the movement is uneven, the concept of average speed is used. Average speed formula: $v_<aver>=frac$, where $s$ is the entire path traveled by the body, $t$ is the entire time of movement. Let's look at an example of a medium speed problem to understand the difference.
Task. Some vehicles cover a distance of 213 km in 2.5 hours. Find it $v_<av>$.
Answer. $85.2 frac<km><h>$ or $23.7frac<m> <s>$.
Cutting speed to diameter Table / Surface speed to RPM conversion
Converting revolutions per minute to linear speed Reference table Cutting speeds depending on the diameter of the cutting tool
Converting revolutions per minute to linear speed Reference table Cutting speeds depending on the diameter of the cutting tool _ Calculation of rotation speed vc Cutting speed (Vc, m/in) Diameter 20 30 40 50 60 70 80 90 100 120 140 150 180 200 250 300 0.2 31.831 47.746 63.662 79.577 95.493 111.408 127.324 143.239 159.155 190.986 222.817 23.872 286.479 318.310 397.887 477.465 0.3 21.2 21 31.831 42.441 53.052 63.662 74.272 84.883 95.493 106.103 127.324 148.545 159.155 190.986 212.207 265.258 318.310 0.4 15.91 5 23.873 31.831 39.789 47.746 55.704 63.662 71.620 79.577 95.493 111.408 119.366 143.239 159.155 198.944 238.732 0.5 12.732 19.099 25.465 31.831 38.197 44.563 50.930 57.296 63.662 76.394 89.127 95.493 114.592 127.324 159.155 190.986 0.6 10, 610 15.915 21.221 26.526 31.831 37.136 42.441 47.746 53.052 63.662 74.272 79.577 95.493 106.103 132.629 159.155 0.7 9.095 13, 642 18,189 22,736 27,284 31,831 36,378 40,926 45,473 54,567 63,662 68,209 81,851 90,946 113,682 136,419 0.8 7.958 11.937 15.915 19.894 23.873 27.852 31.831 35.810 39.789 47.746 55.704 59.683 71.620 79.577 99.472 119.366 0.9 7.0 74 10.610 14.147 17.684 21.221 24.757 28.294 31.831 35.368 42.441 49.515 53.052 63.662 70.736 88.419 106.103 6.366 9.549 12.7 32 15,915 19,009 22,282 25,465 28,648 31,831 38,197 44,563 47,746 57,296 63,662 79,577 95,793 1.5 4.244 6.366 8.488 10.610 12.732 14.854 16.977 19.099 21.221 25.465 29.709 31.831 38.197 42.441 53.052 63.662 2 3.183 4, 775 6.366 7.958 9.549 11.141 12.732 14.324 15.915 19.099 22.282 23.873 28.648 31.831 39.789 47.746 2.5 2.546 3.820 5.093 6.36 6 7.639 8.913 10.186 11.459 12.732 15.279 17.825 19.099 22.918 25.465 31.831 38.197 3 2.122 3.183 4.244 5.305 6.366 7.427 8.488 9.549 10.610 12.732 14.854 15.915 19.099 21.221 26.526 31.831 3.5 1.819 2.728 3.638 4.547 5.457 6.366 7.276 8.185 9.095 10.913 12.732 13.642 16.370 18.189 22.736 27.284 4 1.592 2.387 3.183 3.979 4, 775 5.570 6.366 7.162 7.958 9.549 11.141 11.937 14.324 15.915 19.894 23.873 4.5 1.415 2.122 2.829 3.537 4.244 4.951 5.659 6.366 7.074 8.488 9.903 10.610 12.732 14.147 17.684 21.221 5 1, 273 1.910 2.546 3.183 3.820 4.456 5.093 5.730 6.366 7.639 8.913 9.549 11.459 12.732 15.915 19.099 5.5 1.157 1.736 2.315 2.894 3.472 4.051 4.630 5.209 5.787 6.945 8.102 8.681 10.417 11.575 14.469 17.362 6 1.061 1.592 2.122 2.653 3.183 3.714 4.244 4.775 5.305 6.366 7.427 7.958 9.549 10.610 13.263 15.915 6 .5 979 1.469 1.959 2.449 2.938 3.428 3.918 4.407 4.897 5.876 6.856 7.346 8.815 9.794 12.243 14.691 7 909 1.364 1.819 2.274 2, 728 3.183 3.638 4.093 4.547 5.457 6.366 6.821 8.185 9.095 11.368 13.642 7.5 849 1.273 1.698 2.122 2.546 2.971 3.395 3.820 4.244 5.093 5.942 6.366 7.639 8.488 10.610 12.7 32 8,796 1,194 1,592 1,989 2,387 2,785 3,183 3,581 3,979 4,775 5,570 5,968 7,162 7,958 9,947 11,937 8.5 749 1,123 1,498 1,872 2.247 2.621 2.996 3.370 3.745 4.494 5.243 5.617 6.741 7.490 9.362 11.234 9,707 1.061 1.415 1.768 2.122 2.476 2.829 3.183 3.537 4.244 4.951 5.305 6.366 7.074 8.842 10 .610 9.5 670 1.005 1.340 1.675 2.010 2.345 2.681 3.016 3.351 4.021 4.691 5.026 6.031 6.701 9.377 10.052 10 637 955 1.273 1.59 2 1.910 2.228 2.546 2.865 3.183 3.820 4.456 4.775 5.730 6.366 7.958 9.549 11,579 868 1.157 1.447 1.736 2.026 2.315 2.604 2.894 3.472 4.051 4.341 5.209 5.787 7.23 4 8.681 12 531 796 1.061 1.326 1.592 1.857 2.122 2.387 2.653 3.183 3.714 3.979 4.775 5.305 6.631 7.958 13 490 735 979 1.224 1 .469 1.714 1.959 2.204 2.449 2.938 3.428 3.673 4.407 4.897 6.121 7.346 14,455 682 909 1.137 1.364 1.592 1.819 2.046 2.274 2.728 3.183 3.410 4.093 4.547 5.684 6.821 15,424 637,849 1.061 1.273 1.485 1.698 1.910 2.122 2.546 2.971 3.183 3.820 4.244 5.305 6.366 16,398 597 796,995 1 .194 1.393 1.592 1.790 1.989 2.387 2.785 2.984 3.581 3.979 4.974 5.968 17 374 562 749 969 1.123 1.311 1.498 1.685 1.872 2.247 2.621 2.809 3.370 3, 745 4.681 5.617 18 354 531 707 884 1.061 1.238 1.415 1.592 1.768 2.122 2.476 2.653 3.183 3.537 4.421 5.305 19 335 503 670 838 1.005 1.173 1.340 1.508 1.675 2.010 2.345 2.513 3.016 3.351 4.188 5.026 20 318 477 637 796 955 1.114 1.273 1.432 1.592 1.910 2.228 2.387 2.86 5 3.183 3.979 4.775 21 303 455 606 758 909 1.061 1.213 1.364 1.516 1.819 2.122 2.274 2.728 3.032 9.789 4.547 22 289 434 579 7 23,868 1.013 1.157 1.302 1.447 1.736 2.026 2.170 2.604 2.894 3.617 4.341 23,277 415 554 692 830 969 1.107 1.246 1.384 1.661 1.938 2.076 2.491 2.768 3.460 4.152 24 265 398 531 663 796 928 1.061 1.194 1.326 1.592 1.857 1.989 2.387 2.653 3.316 3.979 25 255 382 509 637 764 891 1.019 1.146 1.273 1.528 1.783 1.910 2.292 2.546 3.183 3.820 gNNNN 28 Influence of the length of the working part (cutter overhang) End mills Influence of the working part on bending deformation Relative length of the working part of the cutter The length of the working part of the cutter is usually measured in the number of its diameters I Id Example) 3D , 15D, 22D The bending deformation is determined by the elastic force, which is proportional to the deflection of the rod. The magnitude of the bending deformation is determined by Hooke's law. As the cutter overhang increases, the bending deformation increases. As the number of teeth increases, the rigidity increases. Small flute size provides higher rigidity. 5 = Relative deformation I = Length of working part P = Cutting force E = Young's modulus I = Moment of inertia ( 1 5 = ltd4 14 >218 >51 -> 51 =851 =52 3
Linear speed
The definition of linear speed refers to the section of physics on mechanics and the subsection on kinematics within the framework of the issue of circular motion. In measuring the speed of movement along a circle, angular speed and linear speed are distinguished.
Let's define linear speed.
Linear velocity $V$ is a physical quantity that shows the path a body has traveled per unit time.
Linear speed formula:
$V=frac$, where $S$ is the path, $t$ is the time during which the point traveled the path $S$.
There is also another version of this formula:
$V=frac$, where $l$ is the path, $t$ is the time during which the point passed along the arc $l$.
In some textbooks, linear velocity is also denoted by the small letter $v$.
There is another formula by which you can find linear speed:
$2pi$ corresponds to a complete circle (360 angular degrees).
$vec V$ is directed tangentially to the trajectory.
Instantaneous Speed Formula
Definition
Instantaneous speed (usually just speed) is a vector quantity equal to the first derivative of the radius vector ($\overline{r}$), which determines the position of a moving material point, with respect to time ($t$):
\[\overline{v}=\frac{d\overline{r}}{dt}=\dot{\overline{r}}\left(1\right).\]
Let's represent the vector $\overline{r}$ in the Cartesian coordinate system as:
\[\overline{r}=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}+z\left(t\right)\overline{k}\ left(2\right),\]
where $\overline{i}$; $\overline{j}$; $\overline{k}$ are unit unit vectors of the corresponding coordinate axes, constant in time, and the formula for speed can be considered the expression:
\[\overline{v}=\overline{i}\frac{dx}{dt}+\overline{j}\frac{dy}{dt}+\overline{k}\frac{dz}{dt}\ left(3\right).\]
The projections of the velocity vector on the coordinate axes X, Y, Z are:
\[\left\{ \begin{array}{c} v_x=\frac{dx}{dt}, \\ v_y=\frac{dy}{dt} \\ v_z=\frac{dz}{dt}. \end{array} \right.(4),\]
We find the magnitude (module) of speed in accordance with the formula:
\[v=\sqrt{v^2_x+v^2_y{+v}^2_z}.\]
If the movement is specified using trajectory parameters, which means: the trajectory and the path function of time ($s(t)$) are known; the path is counted from the trajectory point, which is considered the starting point; each point of the trajectory is characterized by its value $s$; radius - vector is a function of $s,$ and the trajectory can be specified using the equation:
\[\overline{r}=\overline{r}\left(s\right)\left(5\right),\]
in this case, in formula (1) $\overline{r}\left(t\right)$ will be considered as a complex function: $\overline{r}\left[s\left(t\right)\right]$, The speed formula will be:
\[\overline{v}=\frac{d\overline{r}}{dt}=\frac{d\overline{r}}{ds}\frac{ds}{dt}\left(6\right) .\]
The value $\Delta s$ is the distance between two points along the trajectory of the body. Modulus $\left|\Delta \overline{r}\right|$ is the distance between these points along the shortest direction—a straight line. As the two points under consideration come closer, the difference between $\Delta s$ and $\left|\Delta \overline{r}\right|$ decreases. We have:
\[\frac{d\overline{r}}{ds}={\mathop{\lim }_{\Delta s\to 0} \frac{\Delta \overline{r}}{\Delta s}\ } ={\mathop{\lim }_{\Delta s\to 0} \frac{\Delta \overline{r}}{\left|\Delta \overline{r}\right|}\ }\cdot \frac{ \left|\Delta \overline{r}\right|}{\Delta s}=\overline{\tau \ }\left(7\right),\]
where $\overline{\tau \ }$ is a unit vector tangent to the trajectory of the material point. Besides:
\[\frac{ds}{dt}=v(8)\]
module of the speed of movement of a point along a trajectory. Let's represent equation (6) as:
\[\overline{v}=\frac{d\overline{r}}{dt}=\frac{ds}{dt}\overline{\tau \ }=v\overline{\tau \ }\left(9 \right).\]
Formula (9) shows that the instantaneous speed is directed tangentially to the trajectory of the body (material point).