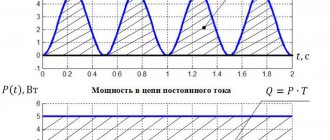
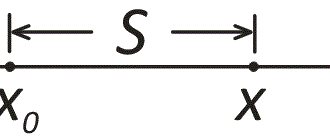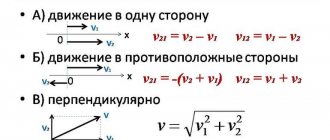Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.
При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:
где:
- N – количество оборотов вокруг оси или по окружности,
- t – время, за которое они были совершены.
В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.
Номинальная скорость вращения
Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:
К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.
Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.
Угловая скорость
Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.
Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.
Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:
где:
- ω – угловая скорость (рад./с);
- ∆ϕ – изменение угла отклонения при повороте (рад.);
- ∆t – время, затраченное на отклонение (с).
Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.
Угловая скорость в конкретных случаях
На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.
Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.
где:
- π – число, равное 3,14;
- ν – частота вращения, (об./мин.).
В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:
Читать также: Артефакт сюита петрушка отзывы
ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.
К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.
Как определить угловую скорость
Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:
Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.
Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.
Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:
ω = ϕ / t = 6 * t / t = 6 с-1
Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.
Скорость сложного движения твердого тела
Разделим обе части выражения (1) на отрезок времени, равный $dt$, получим:
\[\overline{v}=\frac{d\overline{s}}{dt}=\frac{d{\overline{s}}_p}{dt}+\frac{d{\overline{s}}_v}{dt}={\overline{v}}_0+\overline{v’}\left(2\right),\]
где ${\overline{v}}_0$ — скорость поступательного движения точек твердого тела (равна для всех точек); $\overline{v’}$ — скорость вызванная вращением, различается для разных точек тела.
Плоское движение твердого тела можно представить как суму двух движений: поступательного со скоростью ${\overline{v}}_0$ и вращения с угловой скоростью $\overline{\omega }$.
Линейная скорость $\overline{v’}$ точки с радиус-вектором $\overline{r}$, которая возникает в результате вращения тела (линейная скорость вращения точки), равна:
\[\overline{v’}=\left[\overline{\omega }\overline{r}\right]\left(3\right),\]
в выражении (3) имеется в виду векторное произведение. Величина линейной скорости вращения находится как:
\[v’=\omega r{\sin \alpha \ \left(4\right),\ }\]
где $\alpha $ — угол между направлением вектора угловой скорости и радиус-вектором точки (рис.1).
Скорость этой точки при сложном движении представлена формулой:
\[\overline{v}={\overline{v}}_0+\left[\overline{\omega }\overline{r}\right]\left(5\right).\]
В теле могут иметься точки, которые участвуют в поступательном движении и вращении и при этом остаются неподвижными. При известных ${\overline{v}}_0\ $и $\overline{\omega }$ можно найти такой радиус-вектор ($\overline{r}$), что $\overline{v}=0.$
Угол поворота и период обращения
Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.
Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.
Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.
Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.
В этом случае находят применения такие характеристики, как:
- период обращения – T, это время, необходимое для полного оборота точки при круговом движении;
- частота обращения – ν, это полное количество оборотов, которое совершает точка по круговой траектории за единичный временной интервал.
Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.
Циклическая частота вращения (обращения)
Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.
Циклическая частота вращения – это количество оборотов тела за 2*π секунды.
У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.
Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.
При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:
- частоты питающей сети;
- количества пар полюсов.
Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.
Читать также: Колпачки на литые диски реплика
Как изменить скорость работы двигателя?
Изменять скорость вращающего момента механизма оборудования можно различными способами, например, механическими редукторами с переключением передач, муфтами и другими устройствами. Но это не всегда возможно. Практически используется 7 способов коррекции частоты вращения регулируемых приводов. Все способы разделены на два основных направления.
- Коррекция магнитного поля путем воздействия на частоту тока, уменьшение или увеличение числа пар полюсов, коррекция напряжения. Направление характерно моторам с короткозамкнутым (КР) ротором.
- Скольжение корректируется напряжением питания, добавлением еще одного резистора в цепь схемы ротора, установкой двойного питания, использованием каскада вентилей. Такое направление используется для роторов с фазами.
Регулировка частоты и напряжения с помощью частотного преобразователя, путем создания дополнительной катушки с переключением полюсов пар, являются самыми востребованными способами.
Переход от угловой к линейной скорости
Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:
ν = 2*π*R / Т = 2*π*R* ν.
Так как ω = 2*π*ν, то получается:
Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.
К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.
Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:
а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.
Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.
Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.
Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.
Понятие скорости
Когда мы сравниваем движение каких-либо тел, то говорим, что одни тела двигаются быстрее, а другие — медленнее. Такую простую терминологию мы используем в повседневной жизни, говоря, например, о движении транспорта. В физике быстрота движения тел характеризуется определенной величиной. Эта величина называется скоростью. Общее определение скорости (в случае, если тело движется равномерно):
Скорость при равномерном движении тела — это физическая величина, показывающая, какой путь прошло тело за единицу времени.
Под равномерным движением тела подразумевается, что скорость тела постоянна. Формула нахождения скорости: $v=frac$, $s$ — это пройденный телом путь (то есть длина линии), $t$ — время (то есть промежуток времени, за который пройден путь).
Согласно международной системе СИ, единица измерения линейной скорости является производной от двух основных единиц — метра и секунды, то есть измеряется в метрах в секунду (м/с). Это значит, что под единицей скорости понимается скорость такого равномерного движения, при котором путь в один метр тело проходит за одну секунду.
Попробуй обратиться за помощью к преподавателям
Также скорость часто измеряют в км/ч, км/с, см/с.
Рассмотрим простой пример задачи на вычисление скорости.
Задача. Двигаясь равномерно, поезд за 4 ч проходит 219 км. Найти его скорость движения.
Решение. $v=frac<219 км><4 ч>=54,75frac<�км><�ч>$. Переведём километры в метры и часы в секунды: $54,75frac<�км><�ч>=frac<54750 м><3600c>approx 15,2frac<�м>$.
Из примера мы видим, что числовое значение скорости отличается в зависимости от выбранной единицы измерения.
Кроме числового значения, скорость имеет направление. Числовое значение величины в физике называют модулем. Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость — это векторная физическая величина.
На письме модуль скорости обозначается $v$, а вектор скорости — $vec v$.
В свою очередь, такие величины как путь, время, длина и другие характеризуются только числовым значением. Тогда говорят, что это скалярные физические величины.
Читать также: Схема спидометра газ 3110
Задай вопрос специалистам и получи ответ уже через 15 минут!
В случае, когда движение является неравномерным, используют понятие средней скорости. Формула средней скорости: $v_<�ср>=frac$, где $s$ — это весь пройденный телом путь, $t$ — всё время движения. Рассмотрим пример задачи на среднюю скорость, чтобы понять разницу.
Задача. Некоторый транспорт за 2,5 часа преодолевает путь в 213 км. Найти его $v_<�ср>$.
Ответ. $85,2 frac<�км><�ч>$ или $23,7frac<�м> <�с>$.
Скорость резания от диаметра Таблица / Surface speed to RPM conversion
Перевод оборотов в минуту в линейную скорость Справочная таблица Скорости резания в зависимости от диаметра режущего инструмента
Перевод оборотов в минуту в линейную скорость Справочная таблица Скорости резания в зависимости от диаметра режущего инструмента _ Расчет частоты вращения vc Скорость резания (Vc, м/ ин) Диаметр 20 30 40 50 60 70 80 90 100 120 140 150 180 200 250 300 0.2 31,831 47,746 63,662 79,577 95,493 111,408 127,324 143,239 159,155 190,986 222,817 23,872 286,479 318,310 397,887 477,465 0.3 21,221 31,831 42,441 53,052 63,662 74,272 84,883 95,493 106,103 127,324 148,545 159,155 190,986 212,207 265,258 318,310 0.4 15,915 23,873 31,831 39,789 47,746 55,704 63,662 71,620 79,577 95,493 111,408 119,366 143,239 159,155 198,944 238,732 0.5 12,732 19,099 25,465 31,831 38,197 44,563 50,930 57,296 63,662 76,394 89,127 95,493 114,592 127,324 159,155 190,986 0.6 10,610 15,915 21,221 26,526 31,831 37,136 42,441 47,746 53,052 63,662 74,272 79,577 95,493 106,103 132,629 159,155 0.7 9,095 13,642 18,189 22,736 27,284 31,831 36,378 40,926 45,473 54,567 63,662 68,209 81,851 90,946 113,682 136,419 0.8 7,958 11,937 15,915 19,894 23,873 27,852 31,831 35,810 39,789 47,746 55,704 59,683 71,620 79,577 99,472 119,366 0.9 7,074 10,610 14,147 17,684 21,221 24,757 28,294 31,831 35,368 42,441 49,515 53,052 63,662 70,736 88,419 106,103 6,366 9,549 12,732 15,915 19,009 22,282 25,465 28,648 31,831 38,197 44,563 47,746 57,296 63,662 79,577 95,793 1.5 4,244 6,366 8,488 10,610 12,732 14,854 16,977 19,099 21,221 25,465 29,709 31,831 38,197 42,441 53,052 63,662 2 3,183 4,775 6,366 7,958 9,549 11,141 12,732 14,324 15,915 19,099 22,282 23,873 28,648 31,831 39,789 47,746 2.5 2,546 3,820 5,093 6,366 7,639 8,913 10,186 11,459 12,732 15,279 17,825 19,099 22,918 25,465 31,831 38,197 3 2,122 3,183 4,244 5,305 6,366 7,427 8,488 9,549 10,610 12,732 14,854 15,915 19,099 21,221 26,526 31,831 3.5 1,819 2,728 3,638 4,547 5,457 6,366 7,276 8,185 9,095 10,913 12,732 13,642 16,370 18,189 22,736 27,284 4 1,592 2,387 3,183 3,979 4,775 5,570 6,366 7,162 7,958 9,549 11,141 11,937 14,324 15,915 19,894 23,873 4.5 1,415 2,122 2,829 3,537 4,244 4,951 5,659 6,366 7,074 8,488 9,903 10,610 12,732 14,147 17,684 21,221 5 1,273 1,910 2,546 3,183 3,820 4,456 5,093 5,730 6,366 7,639 8,913 9,549 11,459 12,732 15,915 19,099 5.5 1,157 1,736 2,315 2,894 3,472 4,051 4,630 5,209 5,787 6,945 8,102 8,681 10,417 11,575 14,469 17,362 6 1,061 1,592 2,122 2,653 3,183 3,714 4,244 4,775 5,305 6,366 7,427 7,958 9,549 10,610 13,263 15,915 6.5 979 1,469 1,959 2,449 2,938 3,428 3,918 4,407 4,897 5,876 6,856 7,346 8,815 9,794 12,243 14,691 7 909 1,364 1,819 2,274 2,728 3,183 3,638 4,093 4,547 5,457 6,366 6,821 8,185 9,095 11,368 13,642 7.5 849 1,273 1,698 2,122 2,546 2,971 3,395 3,820 4,244 5,093 5,942 6,366 7,639 8,488 10,610 12,732 8 796 1,194 1,592 1,989 2,387 2,785 3,183 3,581 3,979 4,775 5,570 5,968 7,162 7,958 9,947 11,937 8.5 749 1,123 1,498 1,872 2,247 2,621 2,996 3,370 3,745 4,494 5,243 5,617 6,741 7,490 9,362 11,234 9 707 1,061 1,415 1,768 2,122 2,476 2,829 3,183 3,537 4,244 4,951 5,305 6,366 7,074 8,842 10,610 9.5 670 1,005 1,340 1,675 2,010 2,345 2,681 3,016 3,351 4,021 4,691 5,026 6,031 6,701 9,377 10,052 10 637 955 1,273 1,592 1,910 2,228 2,546 2,865 3,183 3,820 4,456 4,775 5,730 6,366 7,958 9,549 11 579 868 1,157 1,447 1,736 2,026 2,315 2,604 2,894 3,472 4,051 4,341 5,209 5,787 7,234 8,681 12 531 796 1,061 1,326 1,592 1,857 2,122 2,387 2,653 3,183 3,714 3,979 4,775 5,305 6,631 7,958 13 490 735 979 1,224 1,469 1,714 1,959 2,204 2,449 2,938 3,428 3,673 4,407 4,897 6,121 7,346 14 455 682 909 1,137 1,364 1,592 1,819 2,046 2,274 2,728 3,183 3,410 4,093 4,547 5,684 6,821 15 424 637 849 1,061 1,273 1,485 1,698 1,910 2,122 2,546 2,971 3,183 3,820 4,244 5,305 6,366 16 398 597 796 995 1,194 1,393 1,592 1,790 1,989 2,387 2,785 2,984 3,581 3,979 4,974 5,968 17 374 562 749 969 1,123 1,311 1,498 1,685 1,872 2,247 2,621 2,809 3,370 3,745 4,681 5,617 18 354 531 707 884 1,061 1,238 1,415 1,592 1,768 2,122 2,476 2,653 3,183 3,537 4,421 5,305 19 335 503 670 838 1,005 1,173 1,340 1,508 1,675 2,010 2,345 2,513 3,016 3,351 4,188 5,026 20 318 477 637 796 955 1,114 1,273 1,432 1,592 1,910 2,228 2,387 2,865 3,183 3,979 4,775 21 303 455 606 758 909 1,061 1,213 1,364 1,516 1,819 2,122 2,274 2,728 3,032 9,789 4,547 22 289 434 579 723 868 1,013 1,157 1,302 1,447 1,736 2,026 2,170 2,604 2,894 3,617 4,341 23 277 415 554 692 830 969 1,107 1,246 1,384 1,661 1,938 2,076 2,491 2,768 3,460 4,152 24 265 398 531 663 796 928 1,061 1,194 1,326 1,592 1,857 1,989 2,387 2,653 3,316 3,979 25 255 382 509 637 764 891 1,019 1,146 1,273 1,528 1,783 1,910 2,292 2,546 3,183 3,820 гНННЬ 28 Влияние длины рабочей части (вылета фрезы) Концевые фрезы Влияние рабочей части на деформацию изгиба Относительная длина рабочей части фрезы Длину рабочей части фрезы принято измерять в количестве её диаметров I Id При мер) 3D, 15D, 22D Деформация изгиба определяется силой упругости.которая пропорциональна прогибу стержня. Вел ичин а деформация изгиба определяется по закону Гука С ув еличением вылета фрезы увеличивается деформация изгиба. С увел ичением количества зубьев жесткость возрастает. Малый размер стружечной канавки обеспечивает более высокую жесткость. 5 = Относительная деформация I = Длина рабочей части P = Сила резания Е = Модуль Юнга I = Момент инерции ( 1 5 = ltd4 14 >218 >51 -> 51 =851 =52 3
Линейная скорость
Определение линейной скорости относится к разделу физики о механике и подразделу о кинематике в рамках вопроса движения по окружности. В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.
Дадим определение линейной скорости.
Линейная скорость $V$ — это физическая величина, показывающая путь, который прошло тело за единицу времени.
Формула линейной скорости:
$V=frac$, где $S$ — путь, $t$ — время, за которое точка прошла путь $S$.
Также существует иной вариант этой формулы:
$V=frac$, где $l$ — путь, $t$ — время, за которое точка прошла по дуге $l$.
В некоторых учебниках линейная скорость также обозначается маленькой буквой $v$.
Есть ещё одна формула, по которой можно найти линейную скорость:
$2pi$ соответствует полной окружности (360 угловым градусам).
$vec V$ направленена по касательной к тракетории.
Формула мгновенной скорости
Определение
Мгновенная скорость (обычно просто скорость) — это векторная величина, равная первой производной от радиус-вектора ($\overline{r}$), определяющего положение движущейся материальной точки, по времени ($t$):
\[\overline{v}=\frac{d\overline{r}}{dt}=\dot{\overline{r}}\left(1\right).\]
Представим вектор $\overline{r}$ в декартовой системе координат в виде:
\[\overline{r}=x\left(t\right)\overline{i}+y\left(t\right)\overline{j}+z\left(t\right)\overline{k}\left(2\right),\]
где $\overline{i}$; $\overline{j}$; $\overline{k}$ — единичные орты соответствующих осей координат, постоянные во времени, при этом формулой скорости можно считать выражение:
\[\overline{v}=\overline{i}\frac{dx}{dt}+\overline{j}\frac{dy}{dt}+\overline{k}\frac{dz}{dt}\left(3\right).\]
Проекциями вектора скорости на оси координат X, Y,Z являются:
\[\left\{ \begin{array}{c} v_x=\frac{dx}{dt}, \\ v_y=\frac{dy}{dt} \\ v_z=\frac{dz}{dt}. \end{array} \right.(4),\]
Величину (модуль) скорости найдем в соответствии с формулой:
\[v=\sqrt{v^2_x+v^2_y{+v}^2_z}.\]
Если движение задается при помощи параметров траектории, что означает: известны траектория и функция пути от времени ($s(t)$); путь отсчитывают от точки траектории, которую считают начальной; каждая точка траектории характеризуется своей величиной $s$; радиус — вектор является функцией от $s,$ и траекторию можно задать при помощи уравнения:
\[\overline{r}=\overline{r}\left(s\right)\left(5\right),\]
в таком случае в формуле (1) $\overline{r}\left(t\right)$ будем рассматривать как сложную функцию: $\overline{r}\left[s\left(t\right)\right]$, формулой скорости станет:
\[\overline{v}=\frac{d\overline{r}}{dt}=\frac{d\overline{r}}{ds}\frac{ds}{dt}\left(6\right).\]
Величина $\Delta s$ — это расстояние между двумя точками по траектории движения тела. Модуль $\left|\Delta \overline{r}\right|$ — расстояние между этими точками по кратчайшему направлению — прямой. При сближении рассматриваемых двух точек разница между $\Delta s$ и $\left|\Delta \overline{r}\right|$ уменьшается. Имеем:
\[\frac{d\overline{r}}{ds}={\mathop{\lim }_{\Delta s\to 0} \frac{\Delta \overline{r}}{\Delta s}\ }={\mathop{\lim }_{\Delta s\to 0} \frac{\Delta \overline{r}}{\left|\Delta \overline{r}\right|}\ }\cdot \frac{\left|\Delta \overline{r}\right|}{\Delta s}=\overline{\tau \ }\left(7\right),\]
где $\overline{\tau \ }$ — единичный вектор, касательный к траектории движения материальной точки. Кроме этого:
\[\frac{ds}{dt}=v(8)\]
модуль скорости движения точки по траектории. Уравнение (6) представим как:
\[\overline{v}=\frac{d\overline{r}}{dt}=\frac{ds}{dt}\overline{\tau \ }=v\overline{\tau \ }\left(9\right).\]
Формула (9) показывает, что мгновенная скорость направлена по касательной к траектории движения тела (материальной точки).