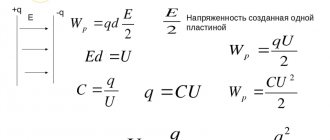Емкостное сопротивление: что это такое, формула, пример расчета

При проектировании электрический цепей, оборудования и электроприборов учитываются многие свойства проводников. Одним из важных свойств считается емкостное сопротивление.

В данной статье будет подробно описано — что такое емкостное сопротивление конденсатора. Так же будет приведена формула расчета такого параметра, описана работа конденсатора в цепи переменного тока и сферы применения ёмкостного сопротивления.

Определение

Сопротивлением называют физический эффект противодействия протеканию тока по любой электрической цепи. Этим свойством обладают все проводники электрического тока. Данная величина измеряется в Ом.

Емкостное электрическое сопротивление является величиной, благодаря которой можно понять, что в цепи присутствует конденсатор. Емкостные сопротивления конденсатора рассчитываются только для цепей переменного тока, без учета наличия в них резисторов.

Конденсатор обозначается на схеме буквой «С», а его ёмкостное сопротивление «Xc».

Емкостное сопротивление конденсатора

Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.

Емкостное сопротивление можно отнести к реактивному, не вызывающему безвозвратных энергетических потерь. Зарядка конденсатора происходит до того уровня напряжения, которое отдается источником питания.

Совершенно по-другому на конденсатор воздействует переменный ток, вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.

Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.

Названия других элементов определяются материалами обычных диэлектриков. Поэтому они относятся к категории бумажных, керамических, стеклянных и т.д. Каждый из них, в соответствии с характеристиками и особенностями, применяется в конкретных электронных схемах, с разными параметрами электротока.

В связи с этим, применение керамических конденсаторов необходимо в тех цепях, где требуется фильтрация высокочастотных помех. Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.

Принцип работы

Конденсатор с определенной ёмкостью работает по принципу периода, который состоит из заряда и разряда элемента. Период делится на 4 части:

Первая часть предполагает рост напряжения. В этот момент сопротивление конденсатора минимально, а зарядный ток очень высокий.
Во второй четверти происходит наполнение его ёмкости за счет зарядного тока.
В третьей четверти конденсатор полностью заряжается, при этом происходит снижение тока вплоть до 0. ЭДС возрастает с эффектом смены своей направленности.
В последней четверти происходит разряд элемента. На этом этапе ЭДС будет в пределах 0, а ток постепенно нарастать.

Все описанные процессы за один период определяют дальнейший фазный сдвиг на 90 градусов.

Природа возникновения емкостного сопротивления полностью зависит от нескольких факторов:

Обязательно наличие конденсатора в цепи.
По цепи должен течь только переменный ток.
Сопротивление проводника должно быть меньше емкости конденсатора.

Все эти факторы помогают рассчитать наиболее правильное значение ёмкостных характеристик для наиболее эффективной работы электроцепи.

Общее описание

Физически электронное устройство — конденсатор — представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.

Слово «конденсатор» произошло от латинского «condensatio» — «накопление». Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).

На схемах конденсатор изображается в виде двух прямых, соответствующих проводящим пластинам прибора, и перпендикулярно к их серединам нарисованными отрезками — выводами устройства.

Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом — отрицательного.

Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток — минимальным.

Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.

Расчет

Расчет электрического емкостного сопротивления цепи делается по формуле. Она состоит из следующих значений:

«Xc» — является емкостным сопротивлением в Омах.
«1» — период полного заряда и разряда элемента.
«w» — круговая частота переменного тока с емкостью, рад/сек.
«C» — емкость конденсатора, единицы измерения Фарад.

Сама формула при этом выглядит следующим образом:

При помощи этой формулы легко рассчитывается Xc. Для этого требуется просто умножить циклическую частоту переменного тока на известную величину емкости конденсатора. Далее необходимо будет один период разделить на полученное значение. Таким образом можно всегда найти сопротивление конденсатора в Ом.

Рассчитываться емкостное сопротивление может так же с помощью и другой формулы, которая приведена на рисунке ниже.

При расчетах по данной формуле прослеживаются следующие зависимости:

Емкость конденсатора и частота тока всегда выше сопротивления.
От величин емкости и частоты зависит скорость одного периода заряда/разряда конденсатора.

Также стоит учесть, что после подключения конденсатора в цепь постоянного тока, его сопротивление сильно увеличивается. Объясняется причина такого явления довольно просто — отсутствует частота протекания электричества.

Переменный ток

Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про сопротивление конденсатора переменному току

. Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.

Сразу оговорюсь про одну важную вещь. Вообще говоря, реальный конденсатор обладает помимо емкостного

сопротивления еще
резистивным
и
индуктивным
. На практике все это надо обязательно учитывать, потому что возможны ситуации (обычно связанные с ростом частоты сигнала), когда конденсатор перестает быть конденсатором и превращается… в некое подобие катушки индуктивности . При проектировании схем этот момент обязательно надо иметь в виду. Согласитесь, господа, крайне неприятно поставить в схему конденсатор и потом столкнуться с тем, что из-за высокой частоты он ведет себя и не как конденсатор вовсе, а как самый настоящий дроссель. Это, безусловно, очень важная тема, но сегодня речь пойдет не о ней. В сегодняшней статье мы будем говорить непосредственно про
емкостное
сопротивление конденсатора. То есть мы будем считать его идеальным, без каких бы то ни было паразитных параметров вроде индуктивности или активного сопротивления.

Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все (рисунок 1).

Рисунок 1 – Конденсатор в цепи переменного тока

К его обкладкам приложено некоторое переменное напряжение U(t), и через него течет некоторый ток I(t). Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока, там мы про все это довольно подробно говорили. Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так

В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом

Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов! Помните, на эту тему была отдельная статья? В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная

запись комплексного числа. Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида

то его можно представить в показательной форме вот так

Почему это так, откуда взялось, что здесь какая буковка значит – обо всем уже подробно говорили. Для повторения можно перейти по ссылке и еще раз со всем ознакомиться.

Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого

Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике. Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Давайте представим, что t=0. Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам

сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой. Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с
амплитудой
сигнала. Сейчас как раз такой момент. Поэтому полагаем
t=0 и получаем комплексную амплитуду напряжения
Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями.

Итак, у нас имеется три множителя. Будем разбираться со всеми по порядку. Объединим первые два и запишем выражение следующего вида

Что мы вообще такое записали? Правильно, комплексную амплитуду тока

через конденсатор. Теперь выражение для комплексной амплитуды напряжения принимает вид

Результат, к которому мы стремимся, уже близок, но остается еще один не очень приятный множитель с экспонентой. Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике, не зря ж я ее писал . Давайте преобразуем этот множитель, воспользовавшись формулой Эйлера:

Да, вся эта хитрая экспонента с комплексными числами в показателе превращается всего лишь в мнимую единичку, перед которой стоит знак минус. Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид

Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома. Получим

Как мы помним из статьи про закон Ома, у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение – переменные и представлены через комплексные амплитуды. Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное
сопротивление конденсатора переменному току
:

Да, выражение для сопротивления конденсатора имеет вот такой вот вид. Оно, как вы можете заметить, комплексное

. Об этом свидетельствует буковка
j в знаменателе дроби. А что значит эта комплексность? На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фазв 90 градусов
между током и напряжением на конденсаторе. А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье. Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это
j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент . Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло.
Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода? Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно.

Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения. Но она не влияет на амплитуды тока и напряжения. Соответственно, если сдвиг фаз нас не интересует

, то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:

Согласитесь, жить стало чуточку легче. Это выражение позволяет рассчитать сопротивление конденсатора для конкретной емкость и частоты сигнала. Заметьте, господа, интересный факт. Сопротивление конденсатора, оказывается, зависит не только от самого конденсатора (а именно его емкости), но и от частоты протекающего тока.

Если вспомнить обычные резисторы, то в них у нас сопротивление зависело только от самого резистора, материала, формы и всего такого прочего, но не зависело от частоты (разумеется, мы говорим сейчас про идеальные резисторы, без всяких паразитных параметров). Здесь все по-другому. Один и тот же конденсатор на разной частоте будет иметь разное сопротивление и через него будет течь ток разной амплитуды при одной и той же амплитуде напряжения.

Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора. И чем больше емкость конденсатора, тем меньше его сопротивление переменному току.

По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах. Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным

. И другое оно в первую очередь из-за того самого пресловутого
j в знаменателе, то есть из-за сдвига фазы. У «обычных» (которые называют активными
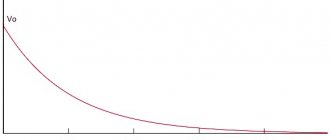
) Омов такого сдвига нет, там напряжение четко совпадает по фазе с током. Давайте построим график зависимости сопротивления конденсатора от частоты. Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ. График представлен на рисунке 2.

Рисунок 2 (кликабельно) – Зависимость сопротивления конденсатора от частоты

На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы.

При стремлении частоты к нулю

(то есть фактически при стремлении переменного току к постоянному) сопротивление конденсатора стремится к бесконечности. Это и логично: мы все помним, что для постоянного тока конденсатор фактически представляет собой разрыв цепи. На практике оно, конечно, не бесконечно, а ограничено сопротивлением утечки конденсатора. Тем не менее, оно все равно очень велико и часто его и считают бесконечно большим.

При стремлении частоты к бесконечности

, сопротивление конденсатора стремится к нулю. Это все в теории, конечно. На практике реальный конденсатор обладает рядом паразитных параметров (в частности, паразитная индуктивности и сопротивление утечки), из-за чего сопротивление уменьшается только лишь до некоторой определенной частоты, а потом начинает наоборот расти. Но об этом более подробно в другой раз.

Есть еще один вопрос, который хотелось бы обговорить, прежде чем начинать рассмотрение примеров. Зачем вообще писать букву j в знаменателе сопротивления? Не достаточно ли просто всегда помнить про сдвиг фаз, а в записи использовать числа без этой мнимой единицы? Оказывается, нет. Представим себе цепь, где одновременно присутствуют резистор и конденсатор. Скажем, они соединены последовательно. И вот тут-то как раз мнимая единичка рядом с емкостью не позволит просто так взять и сложить активное и реактивное сопротивление в одно действительное число. Общее сопротивление такой цепочки будет комплексным, причем состоящим как из действительной части, так и из мнимой. Действительная часть будет обусловлена резистором (активными сопротивлением), а мнимая – емкостью (реактивным сопротивлением). Впрочем, это все тема для другой статьи, сейчас не будем в это углубляться. Давайте лучше перейдем к примерам.

Пусть у нас есть конденсатор емкостью, скажем C=1 мкФ. Требуется определить его сопротивление на частоте f1=50 Гц и на частоте f2=1 кГц. Кроме того, следует определить амплитуду тока с учетом того, что амплитуда приложенного к конденсатору напряжения равна Um=50 В. Ну и построить графики напряжения и тока.

Собственно, задачка эта элементарная. Подставляем циферки в формулу для сопротивления и получаем для частоты f1=50 Гц сопротивление, равное

А для частоты f2=1 кГц сопротивление будет

По закону Ома находим величину амплитуды тока для частоты f1=50 Гц

Аналогично для второй частоты f2=1 кГц

Теперь мы легко можем записать законы изменения тока и напряжения, а также построить графики для этих двух случаев. Полагаем, что напряжение у нас изменяется по закону синуса для первой частоты f1=50 Гц следующим образом

А для второй частоты f2=1 кГц вот так

Дальше мы помним, что ток в конденсаторе опережает напряжение на .

Поэтому с учетом этого можем записать закон изменения тока через конденсаторы для первой частоты
f1=50 Гц
и для частоты f2=1 кГц

Графики тока и напряжения для частоты f1=50 Гц представлены на рисунке 3

Рисунок 3 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f1=50 Гц

Графики тока и напряжения для частоты f2=1 кГц представлены на рисунке 4

Рисунок 4 (кликабельно) – Напряжение на конденсаторе и ток через конденсаторе, f2=1 кГц

Итак, господа, мы сегодня познакомились с таким понятием, как сопротивление конденсатора переменному току, научились его считать и закрепили полученные знания парочкой примеров. На сегодня все. Спасибо что прочитали, всем огромной удачи и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Характеристики элемента

Для того чтобы понять, что такое емкостное сопротивление, необходимо разобраться с его основной характеристикой, которая называется емкостью. Емкостью называется накопительная способность элемента. Она заключается в накоплении определенной доли электрического тока за определённый промежуток времени. Единицей измерения этой величины является Фарад (Ф или F).

Элемент заряжается электричеством до определенного момента, после которого он начинает разряжаться и отдавать ток дальше по электроцепи. Время полного разряда напрямую зависит от величины сопротивления цепи. Чем выше это значение, тем меньше времени тратится на разрядку элемента. Для расчета ёмкостной характеристики используется следующее выражение:

Так же конденсаторы обладают рядом дополнительных характеристик. К ним относят:

Общую удельную емкость. Является отношением массы диэлектрических пластин и емкостных параметров.
Напряжение. Параметр определяется как рабочее напряжение, которое способен выдержать элемент.
Температурная стойкость или стабильность. Это температурный параметр, который не влияет на изменение емкости.
Изоляционное сопротивление. Является величиной точки утечки и саморазряда.
Эквивалентная нагрузка. Значение, определяющее потери на выводе или контактах устройства.
Абсорбция. Разность потенциалов в момент разряда до 0.
Полярность. Параметр свойственен элементам, которые работают строго при подаче на обкладку потенциала определенного значения (плюс или минус).
Индуктивность. Свойство конденсатора образовывать на контактах индуктивное сопротивление. Такое свойство может наделить элемента параметрами колебательного контура.

Все эти значения строго учитываются при проектировании цепей или схем электрического оборудования.

Единица и формулы расчёта

Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.

Математическое выражение фарада

Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.

Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:

пикофарад — 10—12 Ф;
нанофарад — 10—9 Ф;
микрофарад — 10—6 Ф.

Вам это будет интересно Материал, из какого должен изготавливаться искусственный заземлитель

Диэлектрическая проницаемость

Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:

А — площадь меньшей пластины;
d — расстояние между ними;
ε — абсолютная проницаемость используемого диэлектрического материала.

Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.

На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:

1,0006 — воздух;
2,5—3,5 — бумага;
3—10 — стекло;
5—7 — слюда.

Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.

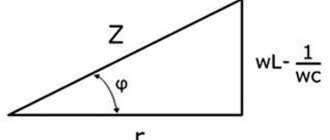
Импеданс

Кроме емкостного, конденсатор еще имеет общее сопротивление или импеданс. Данное значение определяется с учетом значений трех параметров: индуктивного, резистивного и емкостного сопротивления.

Для вычисления импеданса применяется следующая формула:

В данном выражении используются следующие сопротивления:

xL — индуктивное;
xC — емкостное;
R — активное.

Активное сопротивление цепи появляется вследствие возникновения в ней ЭДС. Так как переменный ток по своей природе импульсный, то электромагнитный поток может довольно незначительно изменяться, а это приводит к сдвигу постоянного значения ЭДС.

Емкостные и индуктивные величины взаимосвязаны. По разнице между ними легко находят реактивную составляющую цепи.

Отсюда легко проследить, от чего зависит само реактивное сопротивление:

Если реактивная величина больше 0, то устройство больше нагружено индуктивным значением.
Если реактивное значение равно 0, то емкость не нагружается активным сопротивлением.
Если реактивность меньше 0, то элемент имеет высокое емкостное сопротивление.

Активное сопротивление считается невосполнимой величиной. Она тратится на преобразование тока в иной вид энергии. Реактивная величина неизменна для актуальной цепи переменного тока.

Практическое использование реактивного сопротивления

С помощью конденсаторных установок осуществляется компенсация реактивной мощности. Через электрические сети высоковольтная электроэнергия передается на большие расстояния. В большинстве случаев она потребляется электродвигателями с резистивными элементами и значительным индуктивным сопротивлением.

Полная мощность, поступающая к потребителям, включает в себя активную составляющую Р, с помощью которой совершается полезная работа, и реактивную составляющую Q, приводящую к нагреву обмоток электродвигателей и трансформаторов. Качество электроэнергии существенно снижается под действием реактивной составляющей, возникающей на индуктивных сопротивлениях. Для того чтобы ликвидировать ее негативное воздействие, была разработана специальная схема компенсации. С этой целью подключались конденсаторные батареи, емкостное сопротивление которых способствовало понижению косинуса угла ф.

Установка таких конденсаторных батарей практиковалась в основном на подстанциях, осуществляющих непосредственную поставку электроэнергии проблемным потребителям. Данное мероприятие позволяло эффективно регулировать качество поставляемой энергии.

Снижение уровня реактивной компоненты способствует существенному уменьшению нагрузки на установленное оборудование, хотя активная мощность остается на одном и том же уровне. Используя реактивное сопротивление конденсатора, удалось добиться экономии электроэнергии на предприятиях промышленного производства и объектах жилищно-коммунального хозяйства, повысить надежность работы энергетических систем.

Расчет

Узнав, по какой формуле делаются необходимые вычисления и поняв смысл емкостного сопротивления, можно заняться расчетом данной величины.

Например, сделаем расчет на основе следующих данных:

Емкость конденсатора C=1мкФ;
В цепи также имеется активное сопротивление R, которое равно 5 кОм;
Индуктивное сопротивление цепи xL составляет 4.5 кОм;
Частота переменного тока равна 50 Гц;
Напряжение 50 вольт.

На основе этих данных необходимо будет найти сопротивление конденсатора.

Емкостное сопротивление определим следующим образом:

xC=1/(2πfC)=1/(2×3.14×50×1×10-6)=3184 Ом или округленно 3.2 кОм.

Для определения величины тока в этой цепи воспользуемся законом Ома:

I=U/xC=50/3184=0.0157 ампер или 15.7мА.

После этого определяются параметры общего сопротивления:

Z=(R²+(xL-xC)²)½=(5000²+(4500–3184)²)½=5170 Ом или 5.1 кОм.

По данным расчётам можно определить влияние емкостного элемента на электроцепь. Главное понимать, какие физические величины используются в данных формулах для выполнения правильных вычислений.

Где «прячется» ESR в конденсаторе

ESR представляет из себя сопротивление выводов и обкладок

Как вы знаете, сопротивление проводника можно узнать по формуле:

где

ρ — это удельное сопротивление проводника

l — длина проводника

S — площадь поперечного сечения проводника

Так что можете посчитать приблизительно сопротивление выводов конденсатора и заодно его обкладок Но, конечно же, так никто не делает. Для этого есть специальные приборы, которые умеют замерять этот самый параметр. Например, мой прибор с Алиэкспресса, который я недавно приобрел.

Применение

В электронных цепях очень часто конденсатор используется в качестве фильтрующего элемента. При этом инженеры учитывают способ подключения данного элемента:

При параллельном соединении конденсатора с цепью, устройство способно задерживать ток высокой частоты. Такой фильтр работает по принципу зависимости сопротивления от частоты тока. Чем выше частота, тем ниже будет сопротивление.
При последовательном включении фильтр уже отсеивает низкочастотные импульсы. Вторым свойством такого фильтра является возможность не пропускать постоянный ток.

Также большая доля использования таких устройств приходится на звуковые усилители. Конденсатор способен отделить переменный и постоянный ток, а значит работать в качестве усилителя низкой частоты. При этом подбираются элементы с наименьшей емкостью.

Так же устройства используются для блоков питания постоянного тока или стабилизаторов. Тут применяется свойство разделения постоянной и переменной составляющей. Например, разделение ее между потребителями с помощью отдельных выходов для постоянного и переменного тока. В таких устройствах конденсатор разряжается, если нагрузка на цепь увеличивается за счет подключения нового устройства. Тем самым общая пульсация в цепи сглаживается. При необходимости можно передать ток обоих значений по одному проводнику. Делается это следующим образом — контакты с постоянным напряжением подключают к выводу емкости для прямого контакта с переменным напряжением. Таким образом происходит фильтрация частоты, сглаживание импульсов и передача постоянного тока потребителю. Такая схема используется в антенных усилителях, которые подключаются к телевизорам.

Емкостное сопротивление конденсатора

Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин — электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.

Существуют качества, присущие только конденсаторам. Например, они совершенно не пропускают через себя постоянный ток, хотя и заряжаются от него. После полной зарядки емкости, течение тока полностью прекращается, а внутреннее сопротивление устройства принимает бесконечно высокое значение.

Совершенно по-другому на конденсатор воздействует , вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.

Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.

Измерение и проверка

Измерить целостность конденсатора и его сопротивление можно при помощи мультиметра. Перед этим элемент обязательно необходимо отсоединить от цепи.

Проверка

Диагностика целостности конденсатора начинается с визуально осмотра его состояния. Любые трещины, вздутия или деформации корпуса можно считать неисправностью элемента. Если визуальный осмотр не дал никаких результатов, то элемент проверяется на пробой при помощи тестера.

Делается такая проверка следующим образом:

Элемент необходимо выпаять из схемы, а его контактные выводы замкнуть металлическим предметом для разрядки.
Мультиметр перемести в режим замера сопротивления.
Измерительные щупы соединить с контактами устройства.
Сопротивление исправного элемента будет измеряться бесконечным значением, которое будет превышать значение сопротивления утечки. Величина этой утечки при этом составляет 2 кОм.

Если показания меньше этого значения, значит элемент неисправен и пробит.

Замер

Замерить сопротивление можно так же с помощью мультиметра. Его надо будет перевести в режим измерения сопротивлений более 100 кОм. Далее необходимо соединить щупы прибора с контактами устройства. Некоторое время потребуется на полную зарядку элемента. После этого он покажет конечный результат, который не должен быть выше 100 кОм. Если этот порог преодолен, то можно сделать однозначный вывод о неисправности элемента.

Измерение емкости

Для замера емкости потребуется тестер с режимом СX. Если такого режима нет, проверить элемент будет невозможно. Далее требуется:

Полностью разрядить конденсатор.
На мультиметре выбирается режим СX.
Измерительные щупы соединить с контактными выводами устройства, строго соблюдая полярность.
Прибор должен показать величину больше 1, но при этом ее значение должно быть в пределах тех значений, которые указаны на корпусе детали. Если значение равняется 0 или находится за пределами указанных значений, то конденсатор можно признать неисправным.

Полученные мультиметром данные также можно считать ёмкостным значением, так как в момент проверки элемент проходит зарядку током.

Векторная диаграмма токов в цепи с конденсатором

Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению

I = IG + IC

Действующие величины составляющих тока:

IG = GU (13.31)

IC = BCU (13.32)

Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φa =0). Вектор IG совпадает по направлению с вектором U, а вектор IC направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы IG и IC :

При напряжении u = Umsinωt соответствии с векторной диаграммой уравнение тока

i = Imsin(ωt + φ)

ESR электролитических конденсаторов

В основном параметр ESR касается именно электролитических конденсаторов. Электролит, который там есть, теряет часть своих свойств при нагреве и конденсатор меняет свою емкость, что, конечно же, нежелательно. После приличного нагрева конденсатор начинает тупить, вздувается и быстро стареет.

У вздувшихся конденсаторов в первую очередь как раз ESR и растёт, тогда как ёмкость до определённого времени может оставаться практически номинальной ( ну той, которая написана на самом конденсаторе)

Чаще всего они вспухают в импульсных блоках питания и на материнках, обычно рядом с процессором (там выше на них нагрузка, да и тепло от процессора, вероятно, свою роль играет). Один из характерных симптомов: техника (комп, монитор) начинает включаться всё хуже и хуже. Либо с паузой (до нескольких часов после включения в сеть), либо с -дцатой попытки.

Ещё симптом: если отрубить питание на некоторое время (сетевой фильтр выключить, или из розетки выдернуть) — то снова начинает включаться не с первой попытки, или после паузы. А если не выключать питание, то комп может включаться сразу (но это тоже до поры, до времени, разумеется). Но бывает, что конденсаторы не вспухли, а ESR уже в десятки раз выше нормы. Тогда, понятно, заменяем. По опыту — очень частая проблема. И весьма легко диагностируемая (особенно, при наличии чудо-приборчика от китайских товарищей).