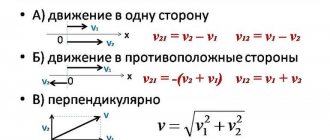Along with motion along a straight line, school physics also considers motion in a circle. For it, by analogy with rectilinear motion, the concepts of distance traveled, speed of movement and acceleration are introduced.
In physics, there are several types of motion of bodies. Circular movement is one of the cases of movement along a curved line - curvilinear movement.
Let's compare the concepts of distance traveled, speed and acceleration for linear motion and circular motion.
Corner path
To begin with, remember that linear displacement is the difference between the final and initial position of a point on an axis (Fig. 1).
\[ S = x – x_{0} \]
Rice. 1. Linear displacement is equal to the difference between the final and initial positions of a point on the axis
Let us now consider the wheel (Fig. 2). On the horizontal line passing through the diameter of the wheel, we will mark a red dot on the right, from which we will begin to count the angles. Let us agree to assume that near this point there is a zero angle.
Rice. 2. The point from position 1 shifted to position 2, passing an angular path
Select a point on the wheel rim, for example a nipple. At first, the nipple was at point 1. Point 1 is shifted by an angle \(\gamma_{1}\) relative to the origin.
We will rotate the wheel in the direction indicated by the blue arrow. Let's turn the wheel at a certain angle so that by the end of the movement the nipple moves to the point indicated by number 2 in the figure. This point is shifted by an angle \(\gamma_{2}\) relative to the origin.
By analogy with translational motion, the angular path that the nipple has traveled is the difference (difference) in the angular positions of points 1 and 2.
\[\large \boxed{ \varphi = \gamma_{2} — \gamma_{1} }\]
\(\varphi \left( \text{rad}\right)\) – the angular path is measured in radians.
The angular path is the angle through which the pin has rotated relative to its initial position.
Mechanical movement and its types
Mechanical motion is a change in the position of a body in space relative to other bodies over time.
Mechanical movement can be: 1. by the nature of the movement
- translational is a movement in which all points of the body move equally and any straight line mentally drawn in the body remains parallel to itself;
- rotational is a movement in which all points of a rigid body move in circles located in parallel planes;
- oscillatory - this is a movement that is repeated in two mutually opposite directions;
2. by type of trajectory
- rectilinear is a movement whose trajectory is a straight line;
- curvilinear is a movement whose trajectory is a curved line;
3. by speed
- uniform - movement in which the speed of the body does not change over time;
- uneven is a movement in which the speed of a body changes over time;
4. by acceleration
- uniformly accelerated is a movement in which the speed of a body increases over time by the same amount;
- equally slow is a movement in which the speed of a body decreases over time by the same amount.
Angular velocity - where is it directed?
If the body moved uniformly (with a constant speed), then the linear speed can be determined by the formula
\
\(v \left( \frac{\text{m}}{c} \right)\) - linear speed is the path divided by time, so it has the dimension of meters divided by second.
Similar to the linear case, if the angular path is divided by the time of movement, we obtain the angular velocity.
\[ \large \boxed{ \omega = \frac{\varphi}{t} } \]
\(\omega \left( \frac{\text{rad}}{c} \right)\) – angular velocity is the angular path divided by time, so it has the dimension of radians divided per second.
Angular velocity \( \omega \), just like linear velocity, is a vector. But unlike linear speed, its direction can be determined by the rule of the gimlet (right screw).
Note: The direction of the angular velocity vector \( \vec{\omega} \) can be determined by the gimlet rule (right screw)!
In Figure 3, the circle is located in the horizontal plane, and the vector \( \vec{\omega }\) is directed along the vertical axis of rotation. The direction of rotation is indicated by a blue arrow.
Rice. 3. Linear and angular velocities of a point rotating in a circle. Angular velocity is directed according to the right screw rule along the axis of rotation
When moving in a circle, the linear velocity vector \(\vec{v}\) changes its direction. But at each point of the circle, the vector \(\vec{v}\) is directed tangent to the circle, that is, perpendicular to the radius.
Note: Tangent and radius are perpendicular, this is known from geometry.
If the point begins to rotate in the opposite direction, then the linear and angular velocity vectors will turn opposite to the directions indicated in Figure 3.
Instant and average speeds
How to find linear speed? The formula, according to the definition of the value, can be written as follows:
v¯ = dl¯/dt.
Where dl¯ is the vector of body displacement during time dt. This speed is called instantaneous because it is calculated over an extremely short period of time dt. Instantaneous speed is actually an unstable and constantly changing quantity. For example, imagine that a car is moving along the road. At first glance, one might believe that at any moment in time its instantaneous speed will be constant, however, this is not the case. Instantaneous speed fluctuates. If the car's speedometer is sensitive enough, it will detect these fluctuations.
You may be interested in:Main neoplasms of preschool age: general characteristics of child development
The formula for average linear velocity is no different from that for instantaneous, however, it is measured over a longer period of time Δt:
v¯ = Δl¯/Δt, where Δt>>dt.
In the car example above, although the instantaneous speed fluctuates, the average speed remains constant with a certain accuracy along the entire path Δl¯.
When solving problems, as a rule, average speed is used. The instantaneous value has meaning only in the case of motion with acceleration.
Relationship between linear and angular velocity
Angular and linear speed are related mathematically. Linear velocity is the vector product of the angular velocity vector and the circle radius vector.
Note: The radius of a circle is a vector, it is directed from the center of the circle to its outer boundary.
Vector view:
\[\large \boxed{ \left[\vec{\omega}, \vec{R} \right] = \vec{v} }\]
Scalar form of recording the velocity relationship:
\[ \large \boxed{ \omega \cdot R = v }\]
\(\omega \left( \frac{\text{rad}}{c} \right)\) – angular velocity;
\(v \left( \frac{\text{m}}{c} \right)\) - linear speed;
\(R \left( \text{m}\right)\) – radius of the circle.
Uniform movement in a straight line
This is an idealized type of motion, which assumes that a body moves along a straight line in space for a certain period of time. In this case, the speed of the body does not change. Denoting the distance traveled by the symbol l, we obtain the formula:
l = v*t.
Here v = const.
This type of movement was considered by the philosophers of Ancient Greece. They believed that for the movement of bodies it is necessary to apply some force, therefore the natural state of all surrounding objects is rest. Only with the advent of the Renaissance, thanks to the work of Galileo and Newton, it was shown that if a body is not affected by external forces, then the uniformity and straightness of its movement is not disturbed.
Frequency and period
Rotational motion is described using characteristics such as frequency and period.
The period of revolution is the time of one complete revolution. In the SI system, the period is measured in seconds.
\( T \left(c \right)\) – the time during which the body made a full revolution – period. Time is a scalar quantity.
Frequency answers the question: “How many full revolutions did the body make in one second?”
\( \displaystyle \nu\left( \frac{1}{c} \right)\) – rotation frequency, scalar.
Instead of writing \( \displaystyle \left( \frac{1}{c} \right)\) sometimes they use \(\displaystyle \left( c^{-1} \right)\), or \( \left( \ text{Hz} \right)\) – Hertz. This is the name of Heinrich Hertz, the famous physicist.
\[\displaystyle 1 \text{Hz} = \frac{1}{c} = c^{-1} \]
Frequency and period are related by inverse proportionality:
\[ \large \boxed{ T = \frac{1}{\nu} } \]
Speed concept
When we compare the movement of any bodies, we say that some bodies move faster, while others move slower.
We use such simple terminology in everyday life, talking, for example, about traffic. In physics, the speed of movement of bodies is characterized by a certain value. This quantity is called speed. General definition of speed (if the body moves uniformly): Definition 1
Velocity during uniform motion of a body is a physical quantity that shows how far the body has traveled per unit time.
By uniform motion of a body it is meant that the speed of the body is constant. The formula for finding speed: $v=\frac{s}{t}$, $s$ is the distance traveled by the body (that is, the length of the line), $t$ is the time (that is, the time period during which the path was traveled).
Are you an expert in this subject area? We invite you to become the author of the Directory Working Conditions
According to the international SI system, the unit of linear speed is derived from two basic units - the meter and the second, that is, it is measured in meters per second (m/s). This means that the unit of speed is the speed of such uniform motion that a body travels a distance of one meter in one second.
Speed is also often measured in km/h, km/s, cm/s.
Let's look at a simple example of a speed calculation problem.
Example 1
Task. Moving uniformly, the train covers 219 km in 4 hours. Find its speed of movement.
Solution. $v=\frac{219 km}{4 h}=54.75\frac{km}{h}$. Let's convert kilometers into meters and hours into seconds: $54.75\frac{km}{h}=\frac{54750 m}{3600c}\approx 15.2\frac{m}{c}$.
Answer. $54.75\frac{km}{h}$ or $15.2\frac{m}{c}$.
From the example we see that the numerical value of the speed differs depending on the selected unit of measurement.
In addition to the numerical value, speed has a direction. The numerical value of a quantity in physics is called the modulus. When a physical quantity also has a direction, then this quantity is called a vector quantity. That is, speed is a vector physical quantity.
Finished works on a similar topic
Course work Formula for calculating linear speed 410 ₽ Abstract Formula for calculating linear speed 220 ₽ Test paper Formula for calculating linear speed 250 ₽
Receive completed work or specialist advice on your educational project Find out the cost
In writing, the velocity module is denoted by $v$, and the velocity vector by $\vec v$.
In turn, such quantities as path, time, length and others are characterized only by a numerical value. Then they say that these are scalar physical quantities.
In the case when the movement is uneven, the concept of average speed is used. Average speed formula: $v_{avg}=\frac{s}{t}$, where $s$ is the entire path traveled by the body, $t$ is the entire time of movement. Let's look at an example of a medium speed problem to understand the difference.
Example 2
Task. Some vehicles cover a distance of 213 km in 2.5 hours. Find it $v_{avg}$.
Solution. $v_{avg}=\frac{213 km}{2.5 h}= 85.2 \frac{km}{h}=\frac{213000 m}{9000 s}\approx 23.7\frac{m }{c} $.
Answer. $85.2\frac{km}{h}$ or $23.7\frac{m}{s}$.
Circular motion problems
How to solve problems involving motion in a circle? Just like everyone else! To get you started, here's a cheat sheet for solving physics problems and a helpful list of formulas. By the way! For all our readers there is a 10% on any type of work .
Task No. 1. Finding linear speed when moving in a circle
Condition
A body moves in a circle with an acceleration of 3 meters per second squared in a circle with a radius of 40 meters. What is the linear speed of the body?
Solution
In this case we mean normal acceleration. Therefore, to solve it, it is enough to remember just one formula:
Answer: 10.9 m/s.
Task No. 2. Finding Angular Acceleration
Condition
The wheel, rotating with constant acceleration, reached an angular velocity of 20 rad/s 10 revolutions after the start of rotation. Find the angular acceleration of the wheel.
Solution
Let us write the law of rotation, taking into account that, according to the condition, the initial angular velocity is equal to zero:
Let us express the angular acceleration from the first equation, and the time from the second. Then we substitute the expressed time into the expression for acceleration and reduce:
Answer: 3.2 radians per second squared.
To convert an angle from radians to degrees, just remember the ratio: in one full rotation there are 2pi radians, or 360 degrees. Therefore, there are approximately 57.3 degrees in one radian.
Task No. 3. Finding the speed of movement in a circle
Condition
How many times is the linear speed of a point on the rim of a wheel with a radius of 8 cm greater than the linear speed of a point located 3 cm closer to the axis of rotation of the wheel?
Solution
The two points rotate on the same wheel, which means they rotate at the same frequency. We use the ratios for speed:
Answer: the speed of a point on the rim is 1.6 times greater.
Task No. 4. Finding the period and frequency when moving in a circle
Condition
The flywheel rotates uniformly and makes N=2400 revolutions in time t=1 min. What is the rotational speed of the flywheel, the period of revolution, and the linear speed of a point located at a distance of 10 centimeters from the center of the flywheel?
Solution
Let’s substitute the values, having previously converted all quantities to the SI system, and calculate:
Answer: 40 Hz; 0.025 s; 25.12 m/s.
Speed when moving in a straight line with acceleration
When an external force appears, its action on the body leads to a change in the speed of the body. In dynamics, this situation is described by Newton’s second law:
F¯ = m*a¯.
If the action of force F¯ occurs on a body of mass m that is initially at rest, then the formula for finding the linear velocity at any moment of time t will take the form:
v¯ = a¯*t.
In this case, both vector quantities are directed in the same direction. This formula can be used to describe the acceleration of any vehicle.
Now suppose that the car was moving at a certain speed v0¯ and then began to stop. In this case, the corresponding kinematic equation will take the form:
v¯ = v0¯ + a¯*t.
Since the velocity module |v¯| the car will decrease over time, in scalar form this equality will be written as follows:
v = v0 - a*t.
In this case, the velocity and acceleration vectors are directed in opposite directions.
All linear velocity formulas given in this paragraph describe linear motion with constant acceleration.