The author of the article is a professional tutor, author of textbooks for preparing for the Unified State Exam Igor Vyacheslavovich Yakovlev
Topics of the Unified State Examination codifier: electromotive force, internal resistance of a current source, Ohm's law for a complete electrical circuit.
Until now, when studying electric current, we have considered the directional movement of free charges in an external circuit
, that is, in the conductors connected to the terminals of the current source.
As we know, positive charge:
• goes into the external circuit from the positive terminal of the source;
• moves in an external circuit under the influence of a stationary electric field created by other moving charges;
• comes to the negative terminal of the source, completing its path in the external circuit.
Now our positive charge needs to close its path and return to the positive terminal. To do this, he needs to overcome the final segment of the path - inside the current source from the negative terminal to the positive. But think about it: he doesn’t want to go there at all! The negative terminal attracts it towards itself, the positive terminal repels it from itself, and as a result, our charge inside the source is acted upon by an electric force directed against
movement of the charge (i.e. against the direction of the current).
Third party force
Nevertheless, current flows through the circuit; therefore, there is a force that “pulls” the charge through the source despite the resistance of the electric field of the terminals (Fig. 1).
Rice. 1. Third party force
This force is called a third party force
;
It is thanks to it that the current source functions. The external force has nothing to do with the stationary electric field - it is said to be of non-electrical
origin; in batteries, for example, it arises due to the occurrence of appropriate chemical reactions.
Let us denote by the work of an external force to move a positive charge q inside the current source from the negative terminal to the positive. This work is positive, since the direction of the external force coincides with the direction of charge movement. The work of an external force is also called the work of a current source
.
There is no external force in the external circuit, so the work done by the external force to move the charge in the external circuit is zero. Therefore, the work of an external force to move a charge around the entire circuit is reduced to the work of moving this charge only inside the current source. Thus, this is also the work of an external force to move charge throughout the circuit
.
We see that the external force is non-potential - its work when moving a charge along a closed path is not zero. It is this non-potentiality that allows the electric current to circulate; a potential electric field, as we said earlier, cannot support a constant current.
Experience shows that work is directly proportional to the charge being moved. Therefore, the ratio no longer depends on the charge and is a quantitative characteristic of the current source. This relationship is denoted by:
(1)
This quantity is called electromotive force
(EMF) of the current source. As you can see, EMF is measured in volts (V), so the name “electromotive force” is extremely unfortunate. But it has long been ingrained, so you have to come to terms with it.
When you see the inscription on the battery: “1.5 V”, then know that this is exactly the EMF. Is this value equal to the voltage created by the battery in the external circuit? It turns out not! Now we will understand why.
Electromagnetic field energy balance. Umov-Pointing vector
Lecture No. 8.
Electromagnetic field energy
Study questions from the lecture:
Third-party sources of electromagnetic fields. Joule-Lenz law.
Electromagnetic field energy balance. Umov-Poynting vector.
Umov-Poynting vector for harmonic fields.
Introduction
This lecture discusses the law of conservation of energy as applied to the electromagnetic field. The physical reality of the electromagnetic field is primarily manifested in the transfer of energy by the field in space . The direct impact of rapidly alternating EMF on the human sense organs causes a sensation of heat, and at a certain vibration frequency – light. However, the main scientific and practical interest is the transformation of field energy into other forms accessible to observation and study, its types and the nature of its distribution in space. For this purpose, the energy balance in a limited area of space will be considered. As a result of the analysis, the concepts of energy flow and Umov-Poynting vector, electric and magnetic energy will appear.
Third-party sources of electromagnetic fields. Joule–Lenz law
The first question introduces the concept of third-party field sources and their consideration in Maxwell’s equations, and formulates the Joule-Lenz law.
When considering electromagnetic processes, one often has to deal with the issue of excitation or creation of a field (for example, in the theory of antennas). The source of the electromagnetic field is usually called an external force (or an external source
).
As a rule, created by some generator not included in the region where the electromagnetic
field is considered are selected as the source of excitation There is an obvious correspondence between external currents (charges) and the fields they create in terms of oscillation frequency and functional dependence on time. Third-party currents and charges are taken into account by introducing them as additional terms in the expressions for conduction current density and volumetric charge density:
; , (1)
where: – density of extraneous conduction current; rst – volumetric density of external electric charge.
The “–” sign means that current or charge is introduced from outside. Taking into account (1), the system of Maxwell’s equations in differential form will take the form :
(2)
Note that in most cases the values and rst are assumed to be given.
Let us determine the work performed by the electromagnetic field when moving a space charge r in an elementary volume ΔV to a distance , where: is the speed of charge movement:
. (3)
Here is the Lorentz force, as shown in lecture No. 4. The parameter Q denotes the amount of charge inside the elementary volume under consideration ΔV . From expression (3) it follows that, firstly, stationary charges cannot produce work , because and, secondly, the magnetic component of the field does not do work , since the direction of the force and the direction of the speed of charge movement are mutually perpendicular, therefore always .
From the course of general physics it is known that power is related to work by the ratio: p = A/t . Therefore, the power released per unit volume ΔV (also called specific power ) can be defined as:
. (4)
Considering that the conduction current density vector is , we now determine the total power released in the volume V :
. (5)
The resulting expression (5) is the well-known Joule-Lenz law in integral form, and expression (4) is, accordingly, the Joule-Lenz law in differential form.
The Joule-Lenz law is a physical law that provides a quantitative assessment of the thermal effect of electric current. It was discovered in 1841 independently by the English physicist James Joule and the Russian physicist of German origin Emil Lenz.
In verbal formulation it sounds as follows - the power of heat released per unit volume of a medium when an electric current flows is proportional to the product of the electric current density and the electric field value.
If the current density is determined only by the conduction current density (as in this case), then the power determined by (5) is the power of heat losses released due to the flow of conduction current. In other words, we are talking about converting electromagnetic energy into other types of energy .
If external forces act in the region V , then equation (5), taking into account expression (1), will take the form:
. (6)
Pst - is called the power of external forces released in volume V , this power characterizes the process of converting energy of various types (for example, mechanical, chemical, etc.) into electromagnetic energy;
Rpot is the power of heat losses released due to the flow of conduction current.
Electromagnetic field energy balance. Umov-Pointing vector
In this question, the law of conservation of energy is formulated in relation to the electromagnetic field, and the physical meaning of the Umov-Poynting vector is given.
Let us select a certain volume V , limited by the surface S , in which there are certain sources of EMF. Since the law of conservation of energy is a fundamental law of physics , it is obvious to state that the energy of field sources is spent on the release of heat (or on the transition to other types of energy), on the accumulation of EMF energy inside volume V and on the transition (radiation) of energy from this volume to the adjacent space to it , that is:
Rst = Rpot + Rzap + Rper (7)
where: Pst – power allocated by third-party sources; Rpo t – heat loss power; Rzap – power spent on the accumulation of EMF energy (stored power); Rper is the power coming out of the volume under consideration.
Let us determine the specific values of the components of expression (7). Let's take the 1st and 2nd Maxwell equations in differential form, taking into account external forces, and multiply the 1st equation by and the 2nd equation by the vector :
(8 a)
(8 b)
Next, we subtract expression (8 a) from (8 b) and the result is:
.
Let us transform the left side of the resulting expression using the well-known identity from vector analysis,
,
where are arbitrary vectors; — denotes a vector product.
As a result, we obtain that the divergence of the scalar product of the electric and magnetic field strength vectors is equal to :
. (9)
Let's integrate this expression over the volume V bounded by a closed surface:
.
Applying the Ostrogradsky–Gauss theorem to the left side of the resulting equation , we obtain:
.
Let us rearrange this expression , leaving on the right side only the component containing the current density of external forces, then finally :
. (10)
The resulting equation (10) is called the Umov-Pointing theorem in integral form . It characterizes the energy balance of the electromagnetic field in a closed volume V, limited by the surface S.
Let us find out the physical meaning of the individual terms included in expression (10).
1) The physical meaning of the integral is clear from expression (6). It characterizes the power of external forces that is released in the volume under consideration V.
2) The expression characterizes the power of heat losses in the volume under consideration V created due to the flow of conduction current .
3) To clarify the physical meaning of the expression, consider a special case :
– let there be no third-party sources in volume V , then Pst = 0;
– in addition, let the boundary S be impenetrable to the electromagnetic field (i.e., it is ideally conducting), then, since there is no field at the boundary S ( and ), then .
In this case, we get:
.
From here we draw the first conclusion : the integral under consideration characterizes a certain power in the volume V. Further, since region V is not connected to the external environment ( S is impenetrable), it follows that the integral under consideration will characterize the power stored in volume V. Since in our case this power is spent on losses (heating of the medium), then, obviously, the stored power Pzap should decrease . This is exactly what the “–” sign corresponds to.
From the course of general physics it is known that power is related to energy as , then:
.
Conclusion : The integral under consideration characterizes the rate of change of electromagnetic energy concentrated inside the region V , in other words , the power stored in this region . The integral characterizes the electric field power concentrated in the volume V , and the integral characterizes the magnetic field power concentrated in the same volume.
4) To clarify the physical meaning of the integral, also consider a special case :
– let there be no losses due to heating of the medium, i.e. Rpo t = 0;
– electromagnetic energy inside region V remains constant, therefore, dW/dt = 0.
In this case we get:
.
From here we can draw the first conclusion : the integral under consideration is the power , in addition, since this integral is taken over a closed surface S, it is the power passing through the surface S. Since there are no losses, and the stored energy is constant in a given volume ( Wzap = const), the power of external forces is spent on the radiation of electromagnetic energy from the volume V under consideration . Consequently, in this case the integral characterizes the radiation power Rizl .
In the case when Pst = 0, W = const, we obtain: , and in this case the integral under consideration characterizes the power that enters through the surface S (note the “–” sign) into the volume V and is spent there in the form of losses .
Conclusion: under consideration characterizes the power, which, depending on the sign, either leaves (“+”) or enters (“–”) through the surface S of the volume V under consideration . Thus, this integral characterizes the power of the transition between the selected volume and the space external to this volume .
The vector product of the components of the electromagnetic field is called the Umov-Poynting vector .
Let's define the unit of measurement for the Umov-Poynting vector . Since it is measured in V/m, and in A/m, it is obvious that the unit of measurement is V × A/m2 = W/m2. Thus, the Umov-Poynting vector characterizes the instantaneous value of the power density passing through a closed arbitrary surface S of one square meter, parallel to the plane in which the vectors and are located.
Based on the above, we write down the electromagnetic field balance equation , which is also called the law of conservation of electromagnetic energy :
. (11)
To conclude this question, consider two particular examples shown in Fig. 1.
a) b)
Rice. 1 – Examples to clarify the meaning of the EMF balance equation
Let us write down the electromagnetic field balance equation for these examples. For the case in Fig. 1a, when a volume in which external forces are present is considered (this role is played by the transmitting antenna), the balance equation takes the form :
Rst = Rpot + Rzap + Rizl = .
For the case in Fig. 1 b, when considering a volume in which there are no external forces , it is obvious that the balance equation will have the form:
Rpot + Rzap = – Rreceive = .
The emission power Rizl or the receiving power Rreceive is the transition power , i.e. power passing through the closed surface S V under consideration .
Conclusion: The specific form of the balance equation is determined by the region V under consideration for given sources of external forces.
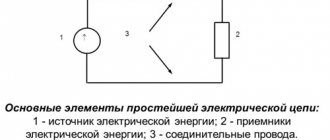
Ohm's law for a complete circuit
Any current source has its own resistance, which is called internal resistance
this source. Thus, the current source has two important characteristics: emf and internal resistance.
Let a current source with an emf equal to and internal resistance be connected to a resistor (which in this case is called an external resistor
, or
external load
, or
payload
).
All this together is called a complete chain
(Fig. 2).
Rice. 2. Complete circuit
Our task is to find the current in the circuit and the voltage across the resistor.
Over time, a charge passes through the circuit. According to formula (1), the current source does the following work:
(2)
Since the current strength is constant, the work of the source is entirely converted into heat, which is released at the resistances and. This amount of heat is determined by the Joule–Lenz law:
(3)
So, , and we equate the right-hand sides of formulas (2) and (3):
After reducing by we get:
So we found the current in the circuit:
(4)
Formula (4) is called Ohm's law for a complete circuit
.
If you connect the terminals of the source with a wire of negligible resistance, you will get a short circuit
.
In this case, the maximum current will flow through the source - short circuit current
:
Due to the small internal resistance, the short circuit current can be quite large. For example, a AA battery gets so hot that it burns your hands.
Knowing the current strength (formula (4)), we can find the voltage across the resistor using Ohm’s law for a section of the circuit:
(5)
This voltage is the potential difference between points and (Fig. 2). The potential of the point is equal to the potential of the positive terminal of the source; the potential of the point is equal to the potential of the negative terminal. Therefore, voltage (5) is also called voltage at the source terminals
.
We see from formula (5) what will happen in a real circuit - after all, it is multiplied by a fraction less than one. But there are two cases when .
1. Ideal current source
. This is the name of a source with zero internal resistance. When formula (5) gives .
2. Open circuit
. Let's consider the current source by itself, outside the electrical circuit. In this case, we can assume that the external resistance is infinitely large: . Then the quantity is indistinguishable from , and formula (5) again gives us .
The meaning of this result is simple: if the source is not connected to the circuit, then a voltmeter connected to the poles of the source will show its EMF
.
From electrostatics to electrokinetics
Between the end of the 18th and the beginning of the 19th century, the work of scientists such as Coulomb, Lagrange and Poisson laid the mathematical foundations for the determination of electrostatic quantities. Progress in the understanding of electricity at this historical stage is obvious. Franklin had already introduced the concept of “amount of electrical substance,” but so far neither he nor his successors have been able to measure it.
Following Galvani's experiments, Volta tried to find evidence that the animal's "galvanic fluids" were of the same nature as static electricity. In his search for truth, he discovered that when two electrodes of different metals come into contact through an electrolyte, both become charged and remain charged despite the circuit being closed by the load. This phenomenon did not correspond to existing ideas about electricity because electrostatic charges in such a case had to recombine.
Volta introduced a new definition of the force acting in the direction of separating charges and maintaining them in this state. He called it electromotive. Such an explanation for the description of battery operation did not fit into the theoretical foundations of physics at that time. In the Coulomb paradigm of the first third of the 19th century. d.s. Volta was determined by the ability of some bodies to generate electricity in others.
Ohm made the most important contribution to the explanation of the operation of electrical circuits. The results of a series of experiments led him to the construction of the theory of electrical conductivity. He introduced the quantity “voltage” and defined it as the potential difference across the contacts. Like Fourier, who in his theory distinguished between the amount of heat and temperature in heat transfer, Ohm created a model by analogy relating the amount of charge transferred, voltage and electrical conductivity. Ohm's law did not contradict the accumulated knowledge of electrostatic electricity.
You might be interested in Description and types of input distribution devices (IDUs)
Then, thanks to Maxwell and Faraday, explanatory models of current received a new field theory. This allowed the development of a field-related energy concept for both static potentials and electromotive force. The main dates for the evolution of the concept of EMF:
- 1800 - creation of the Voltaic galvanic battery;
- 1826 - Ohm formulates his law for a complete chain;
- 1831 - discovery of electromagnetic induction by Faraday.
Electrical circuit efficiency
It's not hard to see why a resistor is called a payload. Imagine it's a light bulb. The heat generated by a light bulb is beneficial
, since thanks to this warmth the light bulb fulfills its purpose - giving light.
Let us denote the amount of heat released by the payload during time .
If the current in the circuit is equal to , then
A certain amount of heat is also released at the current source:
The total amount of heat released in the circuit is equal to:
Electrical circuit efficiency
is the ratio of useful heat to total heat:
The efficiency of the circuit is equal to unity only if the current source is ideal.
How is internal resistance measured?
To determine the value of the characteristic under consideration, measurements are used during a direct short circuit of the terminals, which is called a short circuit. As you know, if you short-circuit the terminals of a source, a significant current will flow between them. This is often the result of carelessness and leads to burning of the insulation and melting of the wire.
During a short circuit, the circuit resistance becomes minimal. By accurately measuring the current in this situation and knowing the voltage at the terminals when there is no load, you can determine the internal resistance of the power supply. To do this you will need the following formula:
r = U / I(deputy), where
- the letter r denotes the internal resistance of the current source;
- U is the potential difference at the battery terminals without connection to the electrical circuit;
- I(deputy) - the current that passes when the terminals are directly connected to each other.
Finding the load value in this way is not always possible or practical, since a short circuit can cause a serious accident.
Therefore, other solutions to the question of how to find the internal resistance of a source are used. For example, using special measuring instruments. The original iMax B6, ToolkinRC M8, M6, M600 chargers are equipped with the function of measuring this parameter.