See also: Heat of combustion
Energy per volume
| Energy Density | |
| SI unit | /3 |
| B SI Base Units | kg m−1s−2 |
| Derivatives from other quantities | U = / |
Energy Density
This is the amount of energy stored in a given system or region of space per unit volume.
It can also be used to provide energy per unit mass, although the precise term for this is specific energy (or gravimetric energy density). Often only useful
or extractable energy is measured, that is, unavailable energy (such as rest mass energy) is ignored.[1] In cosmological and other general relativistic contexts, however, the energy densities considered correspond to the elements of the energy-momentum tensor and therefore include mass energy as well as energy densities associated with pressures described in the next paragraph.
Energy per unit volume has the same physical units as pressure, and in many cases is a synonym: for example, the energy density of a magnetic field can be expressed as (and behaves like) physical pressure, and the energy required to compress a compressed gas further can be determined by multiplying the difference between the gas pressure and the external pressure. pressure by volume change. In short, pressure is a measure of enthalpy per unit volume of a system. And the pressure gradient has the potential to perform Work on the environment by converting enthalpy into work until equilibrium is reached.
Introduction to Energy Density
Materials store different types of energy, and each type of energy requires a specific type of reaction to be released. In order of typical amount of energy released, these types of reactions are nuclear, chemical, electrochemical, and electrical.
Nuclear reactions occur in stars and in nuclear power plants, both of which derive their energy from the binding energy of nuclei. Chemical reactions are used by animals to produce energy from food and by cars to produce energy from gasoline. Liquid hydrocarbons (fuels such as gasoline, diesel and kerosene) are by far the densest known means of economically storing and transporting chemical energy on a very large scale (1 kg of diesel fuel burns with the oxygen contained in ~15 kg of air) . Electrochemical reactions are used by most mobile devices such as laptops and mobile phones to release energy from batteries.
Types of energy intensity
There are several different types of energy content. One is the theoretical total amount of thermodynamic work that can be obtained from a system at a given temperature and pressure for the environment. This is called exergy. The other is the theoretical amount of work that can be obtained from reagents that are initially at room temperature and atmospheric pressure. This is given by modifying the Gibbs Free Energy standard. But as a source of high temperature or for use in a heat engine, the appropriate quantity is the change in standard enthalpy or heat of combustion.
There are two types of calorific value:
- The higher value (HHV), or total heating value, includes all the heat generated when food is cooled to room temperature and any water vapor condenses.
- The lower value (LHV), or net heat of combustion, does not include the heat that may be released when water vapor condenses, and may not include the heat released when it cools completely to room temperature.
A convenient table of HHV and LHV of some types of fuel can be found in reference books.[2]
Higher and lower heating values of fuel combustion
The measured heating value of a fuel depends on what happens to the water during combustion. Recall that the formation of steam requires a lot of heat and that when water vapor turns into a liquid state, a large amount of heat is released. If water remains in a vapor state when fuel is burned and its characteristics are measured, then it contains heat that will not be measured. This way, only the net energy contained in the fuel will be measured. They say that this measures the lower calorific value of the fuel.
.
If, during measurement (or engine operation), water is completely condensed from a vapor state and cooled to the original temperature of the fuel before it begins to burn, a significantly larger amount of heat generated will be measured. In this case, they say that the higher calorific value of fuel combustion
. It should be noted that the internal combustion engine cannot use the additional energy that is released when steam condenses. Therefore, it is more correct to measure the lower calorific value, which is what many manufacturers do when measuring engine fuel consumption. However, American manufacturers often indicate in the characteristics of manufactured engines data taking into account the higher calorific value. The difference between these values for the same engine is approximately 10%. This is not very much, but it leads to confusion if the engine specifications do not specify the measurement method.
Note that the higher and lower heating values apply only to fuels containing hydrogen, for example, gasoline or diesel fuel. When burning pure carbon or carbon monoxide, the higher and lower calorific values cannot be determined, since these substances do not contain hydrogen and, therefore, water is not formed during their combustion.
When fuel is burned in an engine, the actual amount of mechanical work performed as a result of fuel combustion largely depends on the engine itself. Gasoline engines are less efficient in this regard compared to diesel engines. For example, diesel engines of passenger cars have an energy efficiency of 30–40%, while the same value for gasoline engines is only 20–30%.
Energy density in energy storage and fuel
In energy storage applications, energy density relates the energy in the energy storage device to the volume of the storage device, for example a fuel tank. The higher the energy density of a fuel, the more energy can be stored or transported in the same volume. The energy density of a fuel per unit mass is called the specific energy of that fuel. An overall engine using this fuel will produce less kinetic energy due to inefficiency and thermodynamic considerations - hence the engine's specific fuel consumption will always be greater than its rate of motional kinetic energy production.
Widespread implications
Energy density is different from energy conversion efficiency (net output per input) or internal energy (energy input, as harvesting, cleaning, distributing and dealing with pollution all use energy). Large-scale and intensive energy consumption affects and is affected by climate, waste storage, and environmental consequences.
None of the energy storage methods can boast power density, energy density, or energy density. Peukert's Law describes how the amount of useful energy that can be produced (for a lead-acid cell) depends on how quickly it is extracted. To maximize specific energy and energy density, you can calculate the specific energy density of a substance by multiplying the two values together, where the higher the number, the better the substance at efficiently storing energy.
Alternative energy storage options are discussed to increase energy density and reduce charging time.[10][11][12][13]
Gravimetric and volumetric specific energy of some fuels and storage technologies (modified from Gasoline article):
Note. Some values may be inaccurate due to isomers or other irregularities. See Calorific Value for a comprehensive table of the specific energy of important fuels. Note. It is also important to understand that typically chemical fuel density values do not include the weight of oxygen required for combustion. Typically there are two oxygen atoms for every carbon atom and one for every two hydrogen atoms. The atomic weights of carbon and oxygen are similar, but hydrogen is much lighter than oxygen. The figures are presented in this way for those fuels where, in practice, air will only be drawn into the burner locally. This explains the apparently lower energy density of materials that already include their own oxidizer (such as gunpowder and TNT), where the mass of the oxidizer actually adds dead weight and absorbs some of the combustion energy to dissociate and release oxygen to continue the reaction. This also explains some apparent anomalies, such as the sandwich's energy density appearing to be higher than that of a stick of dynamite.
Examples of work units
Many different materials can store energy, from wood to uranium. These materials are known as fuels, and all of these types are used as sources for various systems. When a fuel comes directly from nature (such as crude oil), it is a primary fuel; when a fuel must be modified to be usable (such as gasoline), it is called a secondary source.
The table below shows the energy density for different fuels:
| Fuel | Energy Density (MJ/kg) | Typical Application |
| Tree | 16 | Space heating, cooking |
| Coal | 24 | Power plants, electricity production |
| Ethanol | 26.8 | Gasoline mixture, alcohol, chemical products |
| Biodiesel | 38 | car engine |
| Raw oil | 44 | Petroleum products production |
| Diesel fuel | 45 | Diesel engine |
| Petrol | 46 | Gasoline engines |
| Gas | 55 | Domestic heating, electricity generation |
| Uran-235 | 76 000 000 | Generating electricity using a nuclear reactor |
To visualize these values, compare the energy densities of different fuels.
Energy Content Tables
| This article or section seems to contradict itself . |
| Some of this section's listed sources may not be reliable . |
Unless otherwise noted, the values in the following table are lower calorific values for ideal combustion without taking into account the mass or volume of the oxidizer.
When considering the data in the table, the following unit conversions may be useful: 3.6 = 1 kWh ≈ 1.34 hp⋅h. Energy densities of energy media
| Storage type | Specific energy (MJ/kg) | Energy Density (MJ/L) | Specific energy (Wh/kg) | Energy Density (Wh/L) | How energy is released and comments |
| Antimatter | 89,875,517,874 = ~90 PJ/kg | Depends on the density of the antimatter form | 24,965,421,631,578 = ~25 TWh/kg | Depends on the density of the antimatter form | Annihilation taking into account both the absorbed mass of antimatter and the mass of ordinary matter |
| Hydrogen (fusion) | 639,780,320[14] but at least 2% of them are lost by neutrinos. | Depends on conditions | 177,716,755,600 | Depends on conditions | Reaction 4H →4He |
| Deuterium | 571,182,758[15] | Depends on conditions | 158,661,876,600 | Depends on conditions | Proposed fusion scheme for D + D → 4He, combining D + D → T + H, T + D → 4He + n, n + H → D and D + D → 3He + n, 3He + D → 4He + H, n +H → D |
| Deuterium+tritium | 337,387,388[16] | Depends on conditions | 93,718,718,800 | Depends on conditions | D + T → 4On + n Develops. |
| Plutonium-239 | 83,610,000 | 1,300,000,000–1,700,000,000 (depending on crystallographic phase) | 23,222,915,000 | 370,000,000,000–460,000,000,000 (depending on crystallographic phase) | Heat produced in the fission reactor |
| Plutonium-239 | 31,000,000 | 490,000,000–620,000,000 (depending on crystallographic phase) | 8,700,000,000 | 140,000,000,000–170,000,000,000 (depending on crystallographic phase) | Electricity produced in Fission Reactor |
| Uranus | 80,620,000[17] | 1,539,842,000 | 22,394,000,000 | Heat produced in the breeder reactor | |
| Thorium | 79,420,000[17] | 929,214,000 | 22,061,000,000 | Heat produced in a breeder reactor (Experimental) | |
| Plutonium-238 | 2,239,000 | 43,277,631 | 621,900,000 | Radioisotope thermoelectric generator. Please note that heat is only produced at a rate of 0.57 W/g. | |
| Hydrogen, liquid[18] | 141.86 (HHV) 119.93 (LHV) | 10,044 (HHV) 8,491 (LHV) | 39,405.639 405.6 (HHV) 33 313.9 (LHV) | 2790.0 (HHV) 2358.6 (LHV) | Energy values are given after heating to 25 ° C. |
| Hydrogen, at 690 bar and 25 °C[18] | 141.86 (HHV) 119.93 (LHV) | 5.323 (HHV) 4.500 (l/s) | 39,405.639 405.6 (HHV) 33 313.9 (LHV) | 1478.6 (HHV) 1250.0 (lt. | |
| Hydrogen, gas, 1 ATM, 25 °C[18] | 141.86 (HHV) 119.93 (LHV) | 0.01188 (HHV) 0.01005 (LHV) | 39,405.639 405.6 (HHV) 33 313.9 (LHV) | 3.3 (HHV) 2.8 (LHV) | |
| Diborane[19] | 78.2 | 21,722.2 | |||
| Beryllium | 67.6 | 125.1 | 18,777.8 | 34,750.0 | |
| Lithium borohydride | 65.2 | 43.4 | 18,111.1 | 12,055.6 | |
| Bohr[20] | 58.9 | 137.8 | 16,361.1 | 38,277.8 | |
| Methane (1.013 bar, 15 °C) | 55.6 | 0.0378 | 15,444.5 | 10.5 | |
| LNG (NG at -160°C) | 53.6[21] | 22.2 | 14,888.9 | 6,166.7 | |
| LNG (NG compressed to 250 bar/~3600 psi) | 53.6[21] | 9 | 14,888.9 | 2,500.0 | |
| Natural gas | 53.6[21] | 0.0364 | 14,888.9 | 10.1 | |
| LPG propane[22] | 49.6 | 25.3 | 13,777.8 | 7,027.8 | |
| LPG butane[22] | 49.1 | 27.7 | 13,638.9 | 7,694.5 | |
| Gasoline (petrol)[22] | 46.4 | 34.2 | 12,888.9 | 9,500.0 | Burnt inside internal combustion engines. Thermal efficiency from 20 to 40%. |
| Polypropylene plastic | 46.4[23] | 41.7 | 12,888.9 | 11,583.3 | |
| Polyethylene plastic | 46.3[23] | 42.6 | 12,861.1 | 11,833.3 | |
| Residential heating oil[22] | 46.2 | 37.3 | 12,833.3 | 10,361.1 | |
| Diesel fuel[22] | 45.6 | 38.6 | 12,666.7 | 10,722.2 | Burnt inside internal combustion engines. Thermal efficiency from 25 to 40%. |
| 100LL Avgas | 44.0[24] | 31.59 | 12,222.2 | 8,775.0 | |
| Jet fuel (eg kerosene) | 43[25][26][27] | 35 | Aircraft engine | ||
| Gasohol E10 (10% ethanol 90% gasoline by volume) | 43.54 | 33.18 | 12,094.5 | 9,216.7 | |
| Lithium | 43.1 | 23.0 | 11,972.2 | 6,388.9 | |
| Biodiesel oil (vegetable oil) | 42.20 | 33 | 11,722.2 | 9,166.7 | |
| DMF (2,5-dimethylfuran)[ clarification needed ] | 42[28] | 37.8 | 11,666.7 | 10,500.0 | |
| Crude oil (defined as tonne of oil equivalent) | 41.868 | 37[21] | 11,630 | 10,278 | |
| Polystyrene plastic | 41.4[23] | 43.5 | 11,500.0 | 12,083.3 | |
| Body fat | 38 | 35 | 10,555.6 | 9,722.2 | Metabolism in the human body (efficiency 22%[29]) |
| Butanol | 36.6 | 29.2 | 10,166.7 | 8,111.1 | |
| Gasohol E85 (85% ethanol 15% gasoline by volume) | 33.1 | 25.65[need a quote ] | 9,194.5 | 7,125.0 | |
| Graphite | 32.7 | 72.9 | 9,083.3 | 20,250.0 | |
| Coal, anthracite[6] | 26–33 | 34–43 | 7,222.2–9,166.7 | 9,444.5–11,944.5 | The numbers represent ideal combustion without oxidizer, but the conversion efficiency to electricity is ~36%. |
| Silicon[30] | 1.790 | 4.5 | 500 | 1,285 | Energy accumulated due to the transition of silicon from solid to liquid phase |
| Aluminum | 31.0 | 83.8 | 8,611.1 | 23,277.8 | |
| Ethanol | 30 | 24 | 8,333.3 | 6,666.7 | |
| DME[31][32] | 31.7 (HHV) 28.4 (l/s) | 21.24 (HHV) 19.03 (LHV) | 8,805.68805.6 (HHV) 7,888.9 (LHV) | 5900.0 (HHV) 5 286.1 (LHV) | |
| Polyester plastic | 26.0[23] | 35.6 | 7,222.2 | 9,888.9 | |
| Magnesium | 24.7 | 43.0 | 6,861.1 | 11,944.5 | |
| Coal, bitumen[6] | 24–35 | 26–49 | 6,666.7–9,722.2 | 7,222.2–13,611.1 | |
| PET plastic (unclean) | 23.5[33] | 6,527.8 | |||
| Methanol | 19.7 | 15.6 | 5,472.2 | 4,333.3 | |
| Hydrazine (burnt to N2+ H2O) | 19.5 | 19.3 | 5,416.7 | 5,361.1 | |
| Liquid ammonia (burnt to N2+ H2O) | 18.6 | 11.5 | 5,166.7 | 3,194.5 | |
| PVC plastic (improper combustion is toxic)[ clarification needed ] | 18.0[23] | 25.2 | 5,000.0 | 7,000.0 | |
| Wood[34] | 18.0 | 5,000.0 | |||
| Peat briquette[35] | 17.7 | 4,916.7 | |||
| Sugar, Carbohydrates and Protein[ citation needed ] | 17 | 26.2 (dextrose) | 4,722.2 | 7,277.8 | Metabolism in the human body (efficiency 22%[36]) |
| Calcium[ citation needed ] | 15.9 | 24.6 | 4,416.7 | 6,833.3 | |
| Glucose | 15.55 | 23.9 | 4,319.5 | 6,638.9 | |
| Dry cow dung and camel dung | 15.5[37] | 4,305.6 | |||
| Coal, lignite[ citation needed ] | 10–20 | 2,777.8–5,555.6 | |||
| Sodium | 13.3 | 12.8 | 3,694.5 | 3,555.6 | burned to wet sodium hydroxide |
| Peat | 12.8 | 3,555.6 | |||
| Nitromethane | 11.3 | 3,138.9 | |||
| Sulfur | 9.23 | 19.11 | 2,563.9 | 5,308.3 | burned to sulfur dioxide[38] |
| Sodium | 9.1 | 8.8 | 2,527.8 | 2,444.5 | burned to dry sodium oxide |
| Lithium air battery rechargeable | 9.0[39] | 2,500.0 | Controlled electrical discharge | ||
| Household waste | 8.0[40] | 2,222.2 | |||
| Zinc | 5.3 | 38.0 | 1,472.2 | 10,555.6 | |
| Iron | 5.2 | 40.68 | 1,444.5 | 11,300.0 | burned to iron(III) oxide |
| Teflon plastic | 5.1 | 11.2 | 1,416.7 | 3,111.1 | flammable toxic but non-flammable |
| Iron | 4.9 | 38.2 | 1,361.1 | 10,611.1 | burned to iron(II) oxide |
| Powder | 4.7–11.3[41] | 5.9–12.9 | |||
| TNT | 4.184 | 6.92 | |||
| ANFO | 3.7 | 1,027.8 | |||
| Zinc air battery[42] | 1.59 | 6.02 | 441.7 | 1,672.2 | Controlled electrical discharge |
| A liquid nitrogen | 0.77[43] | 0.62 | 213.9 | 172.2 | Maximum reversible operation at 77.4 K with 300 K reservoir |
| Sodium-sulfur battery | 0.54–0.86 | 150–240 | |||
| Compressed air at 300 bar | 0.5 | 0.2 | 138.9 | 55.6 | Potential energy |
| Latent heat of fusion of ice[ citation needed ] (thermal) | 0.335 | 0.335 | 93.1 | 93.1 | |
| Lithium metal battery | 1.8 | 4.32 | Controlled electrical discharge | ||
| Li-ion battery | 0.36–0.875[46] | 0.9–2.63 | 100.00–243.06 | 250.00–730.56 | Controlled electrical discharge |
| Flywheel | 0.36–0.5 | 5.3 | Potential energy | ||
| Alkaline battery | 0.48[47] | 1.3[48] | Controlled electrical discharge | ||
| Nickel metal hydride battery | 0.41[49] | 0.504–1.46[49] | Controlled electrical discharge | ||
| Lead acid battery | 0.17 | 0.56 | Controlled electrical discharge | ||
| Supercapacitor (EDLC) | 0.01–0.030[50][51][52][53][54][55][56] | 0.006–0.06[50][51][52][53][54][55] | up to 8.57[56] | Controlled electrical discharge | |
| Water at a height of 100 m of the dam | 0.000981 | 0.000978 | 0.272 | 0.272 | The numbers represent potential energy, but the conversion efficiency to electricity is 85–90%.[57][58] |
| Electrolytic capacitor | 0.00001–0.0002[59] | 0.00001–0.001[59][60][61] | Controlled electrical discharge | ||
| Storage type | Energy density by mass (MJ/kg) | Energy density by volume (MJ/L) | Specific energy (Wh/kg) | Energy Density (Wh/L) | How energy is released and comments |
Since 1 J = 10-6 MJ and 1 m3 = 103 L, divide joule/3 by 109
get / = GJ/m3. Divide MJ/L by 3.6 to get kWh/L.
The mechanical energy storage capacity, or toughness, of a Hookean material when deformed to the point of failure can be calculated by calculating the tensile strength multiplied by the maximum elongation divided by two.
The maximum elongation of a Hooke's material can be calculated by dividing the stiffness of that material by its tensile strength. The following table lists these values, calculated using Young's modulus as a measure of stiffness: Mechanical energy power
| Material | Energy density by mass (J/kg) | Stability: Energy density by volume (J/L) | Density (kg/l) | Module for minors (GPa) | Tensile Strength (MPa) |
| Rubber | 1,651–6,605[62] | 2,200–8,900[62] | 1.35[62] | ||
| Steel, ASTM A228 (outlet, 1mm diameter) | 1,440–1,770 | 11,200–13,800 | 7.80[63] | 210[63] | 2,170–2,410[63] |
| Acetals | 908 | 754 | 0.831[64] | 2.8[65] | 65 (maximum)[65] |
| Nylon-6 | 233–1,870 | 253–2,030 | 1.084 | 2–4[65] | 45–90 (maximum)[65] |
| Copper Beryllium 25-1/2 HT (yield) | 684 | 5,720[66] | 8.36[67] | 131[66] | 1,224[66] |
| Polycarbonates | 433–615 | 520–740 | 1.2[68] | 2.6[65] | 52–62 (maximum)[65] |
| ABS plastic | 241–534 | 258–571 | 1.07 | 1.4–3.1[65] | 40 (maximum)[65] |
| Acrylic | 1,530 | 3.2[65] | 70 (maximum)[65] | ||
| Aluminum 7077-T8 (Yield) | 399 | 1120[66] | 2.81[69] | 71.0[66] | 400[66] |
| Steel, stainless, 301-N (output) | 301 | 2,410[66] | 8.0[70] | 193[66] | 965[66] |
| Epoxy resins | 113–1810 | 2–3[65] | 26–85 (maximum)[65] | ||
| Douglas Fir Wood | 158–200 | 96 | .481–.609[71] | 13[65] | 50 (compression)[65] |
| Steel, soft AISI 1018 | 42.4 | 334 | 7.87[72] | 205[72] | 370 (440 Maximum)[72] |
| Aluminum (unalloyed) | 32.5 | 87.7 | 2.70[73] | 69[65] | 110 (maximum)[65] |
| Pine (American Eastern White, Bend) | 31.8–32.8 | 11.1–11.5 | .350[74] | 8.30–8.56 (bend)[74] | 41.4 (bend)[74] |
| Brass | 28.6–36.5 | 250–306 | 8.4–8.73[75] | 102–125[65] | 250 (maximum)[65] |
| Copper | 23.1 | 207 | 8.93[75] | 117[65] | 220 (maximum)[65] |
| Glass | 5.56–10.0 | 13.9–25.0 | 2.5[76] | 50–90[65] | 50 (compression)[65] |
Battery Capacity Table:
Battery Capacity
| Storage device | Energy content (Joule) | Energy type | Typical weight (g) | Typical dimensions (diameter × height in mm) | Typical Volume (ml) | Energy density by volume (MJ/L) | Energy density by mass (MJ/kg) |
| Alkaline AA Battery[77] | 9,360 | Electrochemical | 24 | 14.2 × 50 | 7.92 | 1.18 | 0.39 |
| Alkaline C battery[77] | 34,416 | Electrochemical | 65 | 26 × 46 | 24.42 | 1.41 | 0.53 |
| NiMH AA Battery | 9,072 | Electrochemical | 26 | 14.2 × 50 | 7.92 | 1.15 | 0.35 |
| NiMH C battery | 19,440 | Electrochemical | 82 | 26 × 46 | 24.42 | 0.80 | 0.24 |
| Li-ion 18650 battery | 28,800–46,800 | Electrochemical | 44–49[78] | 18 × 65 | 16.54 | 1.74–2.83 | 0.59–1.06 |
Volumetric electric field density
→ Interesting
Now suppose that there is a continuous distribution of charges, given by the volume density ρ(r→). Then the elementary volume dV contains a charge
dq = ρ(r→)dV,
and formula (39′) takes the following form: W = 1 2 ∫ ρ(r→)ϕ(r→)dV. (16.1)
Some remark must be made to justify the transition (39′)→(42). When passing to the volume distribution, under the integral, generally speaking, one should write
ρ(r→)ϕ′(r→),
understanding by ϕ′(r→) the potential of all charges, with the exception of the elementary charge ρdV. Let's mentally imagine the charge ρdV in the form of a uniformly charged ball of small radius δ with a center at point r→ and with charge density ρ(r→). It is easy to calculate that the potential of this charge at the center of the ball = 3 2 q δ = 3 2 1 δ ⋅4 3πδ3ρ = 2πδ2 ⋅ ρ(r→), and therefore,
ϕ′(r→) = ϕ(r→) − 2πρ(r→)δ2.
From this it is clear that as δ → 0 ϕ′→ ϕ(r→) and the replacement of ϕ′(r→) by ϕ(r→) is thus indeed admissible.
Now we will carry out some identical transformation of expression (42), replacing ρ in the latter, according to the Poisson equation (13), by −1 4πΔϕ and using the vector analysis formula
div(ϕgradϕ) = ϕΔϕ + gradϕ)2;
as a result we get
W = − 1 8π ∫ div(ϕgradϕ)−gradϕ)2]dV = 1 8π ∮ SϕEndS+ 1 8π ∫ V E2dV,
where S is the surface bounding the volume V. If charges occupy a limited volume in space, and the surface S is taken to be a surface of arbitrarily large radius R, then as R →∞ the integral over the surface
since at large distances ϕ and En coincide at least no slower than 1 R and 1 R2 (if, we repeat, the charges occupy a finite volume of space), and the surface grows like R2.
So, as a result of the identical transformation of expression (42), we obtain the formula W = ∫ E2 8πdV (16.2)
in the form of an integral over the entire space occupied by the field, which, in comparison with the original formula (39), has not only a new form, but, essentially, a new meaning, determining the energy density of the electric field in space W = E2 8π. (16.3)
While (39) describes only the interaction energy of different charges (i≠j), formula (42) and the following formula (43) also include the own energy of each of these charges. In terms of the field, we can say that formulas (42), (43) describe the total energy of the electric field, while (39) describes only a part of this energy.
The idea of the electric field energy distributed in space with volumetric density (44) is obtained here on the basis of rigorous reasoning. Now we get expression (44) from considering a specific example. It is clear that no examples of proof of the validity of (44) can be given for the general case. But specific examples can give a clear idea of how relation (44) “works”.
Let's start with a discussion of the auxiliary question of the forces acting on surface charges from the electric field. More specifically, the forces acting on the charges on the surface of a conductor.
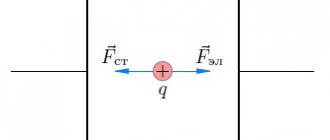
We know that a point charge q is acted upon by the electric field E→
where E→ is the field strength excited by all charges of the system, except for the charge q itself. When we turn to the forces acting on surface charges, a difficulty arises due to the fact that the field E→ has different values on different sides of the surface, and is indefinite on the surface itself. As we have already discussed, inside the conductor the field is identically zero, and on the outside of the surface it has only a normal component associated with the local surface density σ (see Fig. 34). It is clear that the idea of a field discontinuity is due to an implicit refusal to consider the structure of the thin layer where the charges are located, and we assume that this layer is a structureless mathematical surface. This idealization is very productive, allowing us to determine the fields outside and inside the conductor using simple means. The determination of the structure of the surface layer for metal conductors is carried out taking into account the Fermi-Dirac distribution function for conduction electrons and is not yet available to us. But the fact that the surface of the conductor, where the charges are concentrated, actually has a certain finite thickness δ, although very small, where the charges are distributed throughout the volume, makes it possible to easily obtain an expression relating the forces acting on the surface of the conductor to the field strength near this surfaces.
So, let's look at the one highlighted in Fig. 34 section of the surface of the dS conductor. Bearing in mind that the thickness of the layer is very small, the curvature of the surface can be neglected and the surface of the conductor and the layer under consideration can be considered flat.
Let's draw the x-axis along the outer normal to the surface of the conductor and let the layer where the charges are distributed occupy the region (Fig. 35). We can assume that the field E→ inside and near the layer does not depend on the coordinates y, z and has only the x-component Ex(x), and the volume charge density is characterized by the function ρ(x). To the left of this layer the electric field is zero (the field inside the conductor). Therefore, Ex(x) inside the layer satisfies the equation
dEx dx = 4πρ(x),(∗)
boundary condition E(0) = 0 and has the solution
Ex(x) = 4π ∫ 0xρ(ξ)dξ.
Now it is not difficult to find the force acting on the layer,
f→ = fxe→x,fx = ∫ 0δρ(x)E x(x)dx,
per unit surface of the conductor. Substituting here instead of ρ(x) the expression from (*), we obtain
fx = 1 4π ∫ 0δE x(x)dEx dx dx = 1 8π ∫ 0δ d dx2dx,
where E0 = Ex(δ) = 4π ∫ 0δρ(x)dx = 4πσ is the field strength on the outer surface of the conductor.
Thus, the force acting on the surface of the conductor is determined by the total charge σ = ∫ 0δρ(x)dx per unit surface area and does not depend on the distribution ρ(x). Let us note that for any sign of the charge σ, i.e. for any direction of the field E→0, the force f→ is directed along the outer normal, i.e. f→ = E02 8π n→. (16.4)
Note that result (45) is valid for any charged surface if only on one side of the surface the field strength is zero.
Let us now turn to an example intended to illustrate the expression
W = 1 8π ∫ E2dV.
Example 1. Let a spherical surface of radius R be uniformly charged with a total charge q. Having considered the process of expansion of the sphere to a radius R + dR, find an expression for the energy density of the electric field.
in the initial stateEr = q r2 for r > R 0for
in the final stateEr = q r2 for r > R + dR 0for
The fields are shown in Figure 36.
From the side of the electric field, forces with a density act on the sphere
fr = 1 8πE02,E 0 = q R2.
These forces do work
δA = fr ⋅ 4πR2dR = 1 8πE02 ⋅ 4πR2dR.(a)
During the expansion of the sphere, the electric field in space r > R + dR remained unchanged, but in the spherical layer (R, R + dR) it disappeared completely, i.e. the energy of the electric field has changed by the amount
dW = −W ⋅ 4πR2dR,(b)
where W is the desired volumetric energy density.
According to the law of conservation of energy
those. the work δA of electric forces is accomplished due to the decrease in the energy of the electric field. Substituting expressions (a) and (b) here, after reducing by the volume of the layer 4πR2dR we obtain W = 1 8πE02 - what we wanted to see.
Comment. This sphere can be used to solve the inverse problem: assuming that the energy density W is known to us, find the surface force fr per unit surface of the charged sphere from the side of the electric field. The solution is obvious.
As a second example, let us calculate the field energy of a uniformly charged ball of radius a
Er = q r2 for r ≥ R q a3 r for r
W = 1 8π ∫ 0aq2 a6r2 ⋅ 4πr2dr + 1 8π ∫ a∞q2 r44πr2dr = 3 5 q2 a .
Let us use the result obtained to introduce the concept of “classical particle radius”.
According to the theory of relativity, a field with energy W has mass m = W∕c2. Consequently, any particle with mass m and charge q cannot have a size smaller
because the mass of a particle cannot be less than the mass of its field (when writing this formula, the constant 3/5 is not taken into account).
For example, for an electron
re = e2 mc2 ≃ 2.8 ⋅ 10−13cm.
Let two charges q 1 and q 2 be at a distance r from each other. Each of the charges, being in the field of another charge, has potential energy P. Using P = qφ, we define
P 1 =W 1 =q 1 φ 12 P 2 =W 2 =q 2 φ 21
(φ 12 and φ 21 are respectively the field potentials of charge q 2 at the point where charge q 1 is located and charge q 1 at the point where charge q 2 is located).
According to the definition of point charge potential
Hence.
or
Thus,
The energy of the electrostatic field of a system of point charges is equal to
(12.59)
(φ i is the potential of the field created by n -1 charges (except for qi) at the point where charge qi is located).
- Energy of a solitary charged conductor
An isolated uncharged conductor can be charged to potential φ by repeatedly transferring portions of charge dq from infinity to the conductor. The elementary work that is done against the field forces is in this case equal to
Transfer of charge dq from infinity to a conductor changes its potential to
(C is the electrical capacitance of the conductor).
Hence,
those. when transferring charge dq from infinity to a conductor, we increase the potential energy of the field by
dP = dW =δA= Cφdφ
By integrating this expression, we find the potential energy of the electrostatic field of a charged conductor as its potential increases from 0 to φ:
(12.60)
Applying the relation
, we obtain the following expressions for potential energy:
(12.61)
(q is the charge of the conductor).
- Energy of a charged capacitor
If there is a system of two charged conductors (capacitor), then the total energy of the system is equal to the sum of the own potential energies of the conductors and the energy of their interaction:
(12.62)
(q is the charge of the capacitor, C is its electrical capacity.
Taking into account the fact that Δφ=φ 1 –φ 2 = U is the potential difference (voltage) between the plates), we obtain the formula
(12.63)
The formulas are valid for any shape of capacitor plates.
A physical quantity numerically equal to the ratio of the potential field energy contained in a volume element to this volume is called
volumetric energy density.
For a uniform field, the volumetric energy density
(12.64)
For a flat capacitor whose volume is V=Sd, where S is the area of the plate, d is the distance between the plates,
But
,
Then
(12.65)
(12.66)
(E is the electrostatic field strength in a medium with dielectric constant ε, D = ε ε 0 E is the electric field displacement).
Consequently, the volumetric energy density of a uniform electrostatic field is determined by the intensity E or displacement D.
It should be noted that the expression
And
valid only for an isotropic dielectric, for which the relation p = ε 0 χE holds.
Expression
corresponds to field theory - the theory of short-range action, according to which the carrier of energy is the field.
Ferroelectrics. Their features. Piezo effect.
Ferroelectrics,
crystalline dielectrics that have spontaneous (spontaneous) polarization in a certain temperature range, which changes significantly under the influence of external influences.
Piezoelectric effect
— the effect of dielectric polarization under the influence of mechanical stress
- Conductors in an electric field. Distribution of charges in a conductor.
Ε = Evn. - Evn. = 0
Let's introduce a conductor plate into an electric field, let's call this field external.
As a result, the left surface will have a negative charge, and the right surface will have a positive charge. Between these charges, an electric field of its own will arise, which we will call internal. Inside the plate there will simultaneously be two electric fields - external and internal, opposite in direction.
- Electrical capacity of conductors. Capacitor. Connection of capacitors.
Electrical capacity
- a physical quantity numerically equal to the amount of charge that must be imparted to a given conductor to increase its potential by one.
Capacitor
- a device for accumulating charge and energy of an electric field.
parallel connected
series connected
- Energy of a charged conductor, capacitor. Electric field energy. Volumetric energy density of the electric field.
Energy of a charged conductor
equal to the work that must be done to charge this conductor:
Energy of a charged capacitor
Electrostatic field energy
Volumetric energy density of the electrostatic field
16. Electric field strength and density. EMF. Voltage.
Current strength
- a scalar physical quantity determined by the ratio of the charge Δq passing through the cross section of the conductor during a certain period of time Δt to this period of time.
Current density j
is a vector physical quantity, the modulus of which is determined by the ratio of the current strength I in the conductor to the cross-sectional area S of the conductor.
Electromotive force (EMF)
- a physical quantity characterizing the work of third-party (non-potential) forces in direct or alternating current sources. In a closed conducting circuit, the EMF is equal to the work of these forces to move a single positive charge along the circuit.
Electrical voltage
- a physical quantity, the value of which is equal to the ratio of the work of the electric field performed when transferring a test electric charge from point A to point B to the value of the test charge.
17. Ohm's law for a homogeneous section of a chain. Ohm's law for an inhomogeneous area in integral form. Ohm's law for a complete circuit.
current strength I in a homogeneous metal conductor
is directly proportional to the voltage U at the ends of this conductor and inversely proportional to the resistance R of this conductor
Ohm's law for an inhomogeneous section of a circuit in integral form
IR = (φ1 - φ2) + E12
Ohm's law for a complete circuit
:
18. Differential form of Ohm's law.
j-current density, σ - specific electrical conductivity of the substance from which the conductor is made Est-field of external forces
19. Joule-Lenz law in integral and differential forms.
in differential form:
thermal power density -
in integral form:
20. Nonlinear elements. Calculation methods with nonlinear elements. Kirchhoff's rule.
nonlinear
are called electrical circuits in which reactions and effects are related nonlinearly.
Simple iteration method
1. The original nonlinear equation of the electrical circuit, where is the desired variable, is presented in the form .
2. Calculation is performed using the algorithm where
Iteration step. Linear dependencies
Here is the specified error
Kirchhoff's first rule:
the algebraic sum of current strengths converging at a node is equal to zero
Kirchhoff's second rule:
in any simple closed circuit, arbitrarily chosen in a branched electrical circuit, the algebraic sum of the products of current strengths and the resistances of the corresponding sections is equal to the algebraic sum of the emfs present in the circuit
21. Current in a vacuum. Emission phenomena and their technical applications.
Vacuum is a state of gas in a vessel in which molecules fly from one wall of the vessel to another without ever colliding with each other.
A vacuum insulator, a current in it can only arise due to the artificial introduction of charged particles; for this purpose, the emission (emission) of electrons by substances is used. Thermionic emission occurs in vacuum tubes with heated cathodes, and photoelectron emission occurs in a photodiode.
Thermionic emission
is the emission of electrons by heated metals. The concentration of free electrons in metals is quite high, therefore, even at average temperatures, due to the distribution of electron velocities (energies), some electrons have sufficient energy to overcome the potential barrier at the metal boundary. With increasing temperature, the number of electrons, the kinetic energy of thermal motion of which is greater than the work function, increases, and the phenomenon of thermionic emission becomes noticeable.
The phenomenon of thermionic emission is used in devices in which it is necessary to obtain a flow of electrons in a vacuum, for example in vacuum tubes, X-ray tubes, electron microscopes, etc. Electron tubes are widely used in electrical and radio engineering, automation and telemechanics for rectifying alternating currents, amplification electrical signals and alternating currents, generating electromagnetic oscillations, etc. Depending on the purpose, additional control electrodes are used in the lamps.
Photoelectron emission
is the emission of electrons from a metal under the influence of light, as well as short-wave electromagnetic radiation (for example, X-rays). The main principles of this phenomenon will be discussed when considering the photoelectric effect.
Secondary electron emission
- is the emission of electrons from the surface of metals, semiconductors or dielectrics when bombarded with a beam of electrons. The secondary electron flow consists of electrons reflected by the surface (elastically and inelastically reflected electrons), and “true” secondary electrons - electrons knocked out of the metal, semiconductor or dielectric by primary electrons.
The phenomenon of secondary electron emission is used in photomultiplier tubes.
Vehicle emission
is the emission of electrons from the surface of metals under the influence of a strong external electric field. These phenomena can be observed in the evacuated tube.
22. Current in gases. Independent and non-independent conductivity of gases. CVC of current in gases. Types of discharges and their technical applications.
Under normal conditions, gases are dielectrics, because consist of neutral atoms and molecules, and they do not have a sufficient number of free charges. To make a gas conductive, you need to introduce or create free charge carriers—charged particles—in one way or another. In this case, two cases are possible: either these charged particles are created by the action of some external factor or introduced into the gas from the outside, or they are created in the gas by the action of the electric field itself existing between the electrodes. In the first case, the conductivity of the gas is called non-independent, in the second - independent.
Current-voltage characteristic (volt-ampere characteristic
) - a graph of the dependence of the current through a two-terminal network on the voltage on this two-terminal network. The current-voltage characteristic describes the behavior of a two-terminal circuit at direct current.
Glow discharge
observed at low gas pressures. Used for cathode sputtering of metals.
Spark discharge
often observed in nature is lightning. The principle of operation of a spark voltmeter is a device for measuring very high voltages.
Arc discharge
can be observed under the following conditions: if, after igniting the spark discharge, the resistance of the circuit is gradually reduced, then the current strength in the spark will increase. The electric arc is a powerful light source and is widely used in projection, floodlight and other lighting installations. Due to its high temperature, the arc is widely used for welding and cutting metals. High arc temperatures are also used in the construction of electric arc furnaces, which play an important role in modern electrometallurgy.
Corona discharge
observed at relatively high gas pressures (for example, at atmospheric pressure) in a sharply inhomogeneous electric field. It is used in technology for the installation of electric precipitators designed to purify industrial gases from solid and liquid impurities.
23. Magnetic field. Magnetic induction. Magnetic interaction of currents.
A magnetic field
- a force field acting on moving electric charges and on bodies with a magnetic moment, regardless of the state of their motion, the magnetic component of the electromagnetic field.
Magnetic induction
is a vector quantity that is a force characteristic of the magnetic field (its action on charged particles) at a given point in space. Determines the force with which the magnetic field acts on a charge moving at speed .
We will charge a flat capacitor by transferring small portions of charge dq
from one plate to another (Fig. 4.12.) In order to transfer charge
dq
between plates with a potential difference (j 1 – j 2), it is necessary to do work
dA
= (j 1 – j 2)
dq
(4.11)
Considering that, this work can also be written like this:
In order to impart charge Q
, work needs to be done
This work is equal to the energy of a charged capacitor
(4.12)
Here is the voltage across the capacitor, equal to the potential difference across its plates.
Let us continue the transformations of equation (4.12).
Recall that the capacitance of a parallel-plate capacitor
and voltage is related to the electric field strength
U
=
E
∙
d
Using these relations, we write the energy of a charged capacitor in this form
These two expressions for the energy of a capacitor
lead to the following fundamental question: where is the energy located in the capacitor? Where is it “localized”?
If it is associated with electric charges, then it is located on the plates of the capacitor. If this is the energy of the electric field, then it occupies the space between the plates, the volume of which is equal to the volume of the capacitor V
=
S
∙
d
.
To answer this question, it would be necessary to remove the charge from the plates, but leave the field. Then one could see: the energy remained, which means it is connected to the field; if it disappeared, it means it was located together with the charge on the plates.
But the problem is that when the charges are removed, their electrostatic field also disappears, of course. Therefore, the question of energy localization within the framework of electrostatics
cannot be resolved.
In electrodynamics variables
Electric and magnetic fields, as is known, can exist without electric charges. Moreover, such fields have energy, which is direct experimental evidence that this energy is associated with electric fields and is localized in the volume occupied by the field. Now the last expression for the energy of a charged capacitor becomes clearer:
The energy of a capacitor is related to its electric field and is therefore proportional to the volume of the capacitor ( V
), that is, the volume of the field.
The ratio represents the average value of energy per unit volume of the field.
This characteristic of the energy saturation of the field is called “volumetric energy density”.
Usually this characteristic is of a point, local nature. dV is selected around a given point
and calculate the energy density by dividing the energy of this region
dW
by its volume
The volumetric energy density at a given point of the electric field is proportional to the square of the field strength at this point. The volumetric energy density is measured, of course, in J/m 3:
Knowing how the energy density changes in space, we can calculate the energy concentrated in volume V
, electric field:
Conducting ball of radius R
carries a
charge Q. What is the energy of the electric field of this ball?
There is no field inside a charged ball, but outside the ball it coincides with the field of a point charge:
, r
³
R
Volumetric energy density of such a field
Let us calculate the energy concentrated in a spherical layer of thickness dr
(Fig. 4.13.)
Nuclear energy sources
The greatest source of energy is mass itself. This energy, E = mc2
, where
m = ρV
,
ρ
is mass per unit volume,
V
is the volume of the mass itself and
c
is the speed of light.
This energy, however, can only be released by the processes of nuclear fission (0.1%), thermonuclear reaction (1%), or annihilation of part or all of the matter in volume V
by matter-matter collision (100%).[
citation needed
] Nuclear reactions cannot be realized by chemical reactions such as combustion. Although higher matter densities can be achieved, the density of a neutron star will approach the densest system capable of annihilating matter and antimatter. And a black hole, although denser than a neutron star, does not have an equivalent form of antiparticle, but offers the same 100% mass-to-energy conversion rate in the form of Hawking radiation. In the case of relatively small black holes (smaller than astronomical objects), the power output will be enormous.
The sources of energy of the highest density besides antimatter are: fusion and fission. Fusion includes energy from the sun that will be available for billions of years (in the form of sunlight), but for now (2018) fusion energy production is still elusive.
The power from the fission of uranium and thorium into nuclear plant energy will be available for many decades or even centuries due to the abundance of the elements on earth,[79] although the full potential of this source can only be realized through breeder reactors, which other than the BN-600 reactor , not yet used commercially.[80]Coal, gas, and oil are the current primary sources of energy in the United States.[81] but have a much lower energy density. Burning local biomass fuel supplies household energy needs (cooking fires, oil lamps, etc.) around the world.
Thermal power of nuclear fission reactors
The thermal energy density contained in the core of a light water reactor (PWR or BWR) is typically 1 GW (1000 MW electrical power corresponds to ~3000 MW thermal) ranging from 10 to 100 MW thermal energy per cubic meter of cooling water depending on the location in the system being considered (the core itself (~ 30 m3), the reactor vessel (~ 50 m3) or the entire primary circuit (~ 300 m3)). This represents a significant energy density that requires, under all circumstances, a continuous flow of water at high speed so that the heat can be removed from the core even after a reactor shutdown. Failure to cool the three boiling water reactor (BWR) cores at Fukushima in 2011 following the tsunami and the resulting loss of external power and cold source caused the three cores to melt in just a few hours, although the three reactors were properly shut down immediately after the Tōhoku earthquake. This extremely high power density distinguishes nuclear power plants (NPPs) from any thermal power plants (burning coal, fuel or gas) or any chemical plants and explains the large redundancy required to continuously monitor neutron reactivity and to remove residual heat from the nuclear power plant core.
Energy density of an ideal gas[ | ]
The energy density of an ideal gas can be calculated through pressure, or through molecular/molar density and temperature:
w = 1 γ − 1 p = 1 γ − 1 nk T = 1 γ − 1 ν RT = 1 γ − 1 ρ MRT {\displaystyle w={\frac {1}{\gamma -1}}p={\ frac {1}{\gamma -1}}nkT={\frac {1}{\gamma -1}}\nu RT={\frac {1}{\gamma -1}}{\frac {\rho } {M}}RT} ,
where p {\displaystyle p} is the gas pressure, γ {\displaystyle \gamma } is the adiabatic exponent, n {\displaystyle n} is the number of molecules per unit volume, k {\displaystyle k} is Boltzmann's constant, T {\displaystyle T } is the absolute temperature, ν {\displaystyle \nu } is the molar density, R {\displaystyle R} is the gas constant, ρ {\displaystyle \rho } is the density, M {\displaystyle M} is the molar mass.
Energy density of electric and magnetic fields
Main article: Radiant energy density
Electric and magnetic fields store energy. In a vacuum (volume) energy density is given by
u = ε 0 2 E 2 + 1 2 μ 0 B 2 { displaystyle u = { frac { varepsilon _ {0} } {2} } mathbf {E} ^{2} + { frac {1} {2 mu _{ 0}}} mathbf {B } ^ {2}}
where E
is the electric field and
B
is the magnetic field. The solution will be (in SI units) in Joules per cubic meter. In the context of magnetohydrodynamics, the physics of conducting fluids, magnetic energy density behaves like an additional pressure that adds to the gas pressure of a plasma.
In normal (linear and non-dispersed) substances, the energy density (in SI units) is equal to
u = 1 2 ( E ⋅ D + H ⋅ B ) { Displaystyle u = { frac {1} {2} } ( mathbf {E} cdot mathbf {D} + mathbf {H} cdot mathbf {B})}
where D
this is the displacement electric field and
HH
is the magnetizing field.
In the absence of magnetic fields, using Fröhlich Relations these equations can also be extended to anisotropic and nonlinear dielectrics, and to calculate the correlated Helmholtz free energy and density entropy.[82]
When the pulsating laser hits a surface, the radiant exposure, i.e. energy released per unit surface can be called energy density
or fluence.[83]
Energy density of an elastic body[ | ]
During linear deformation, the energy density stored by an elastic body is equal to:
w = 1 2 τ ij ε ij = 1 2 cijkl ε ij ε kl {\displaystyle w={\frac {1}{2}}\tau _{ij}\varepsilon _{ij}={\frac {1} {2}}c_{ijkl}\varepsilon _{ij}\varepsilon _{kl}}
where ε ij {\displaystyle \varepsilon _{ij}} is the deformation tensor, τ ij {\displaystyle \tau _{ij}} is the stress tensor, cijkl {\displaystyle c_{ijkl}} is the elasticity tensor.
In the simplest case (compression-tension), the elastic energy density is equal to
w = E ε 2 2 {\displaystyle w={\frac {E\varepsilon ^{2}}{2}}}
where ε {\displaystyle \varepsilon } is the relative deformation, E {\displaystyle E} is the Young's modulus.
Footnotes
- "Two Classes of SI Units and SI Prefixes". NIST Guide to SI
. 2009-07-02. Retrieved 2012-01-25. - "Fossil and Alternative Fuels - Energy Content (2008)." Engineering ToolBox. Retrieved 2018-10-08.
- Jeong, Gujin; Kim, Hansu; Park, Chung Hwan; Jeong, Jaehwan; Jin, Xing; Song, Juhe; Kim, Bo-ram; Park, Min-Sik; Kim, Ji Man; Kim, Young-Joon (2015). "Nanotechnology Enables Rechargeable Li-SO2 Batteries: Another Approach to Post-Lithium-Ion Battery Systems." Energy and ecology
.
8
(11):3173–3180. Doi:10.1039/C5EE01659B. - "Panasonic is developing new high-capacity 18650 lithium-ion cells." Green Car Congress. Np, December 25, 2009. Web.
- Stura, Enrico; Nicolini, Claudio (2006). "New nanomaterials for lightweight lithium batteries". Analytica Chimica Acta
.
568
(1–2):57–64. doi:10.1016/j.aca.2005.11.025. PMID 17761246. - ^ a b c
Fisher, Julia (2003).
Ehlert, Glenn (ed.). "Energy Density of Coal". Physics Fact Book
. Received 2019-07-28. - "Thermal Values of Various Fuels - World Nuclear Association." World Nuclear Association. Np, September 2016. Web.
- "Overview of the U.S. Department of Energy's Hydrogen Storage Development Program." Office of Energy Efficiency and Renewable Energy Sources. Np, May 2000. Web.
- Wong, Kaufui; Dia, Sarah (2017). "Nanotechnology in batteries." Journal of Energy Resources Technology
.
139
. doi:10.1115/1.4034860. - Ionescu-Zanetti, C.; and others. (2005). "Gap Capacitors: Sensitivity to Changes in Sample Dielectric Constant". Journal of Applied Physics
.
99
(2): 024305. Bibcode:2006JAP…. 99b4305I. doi:10.1063/1.2161818. S2CID 120910476. - Naoi, K.; and others. (2013). “New generation” nanohybrid supercapacitor.” Chemical Research Reports
.
46
(5):1075–1083. Doi:10.1021/ar200308h. PMID 22433167. - Hubler, A.; Osuagwu, O. (2010). "Digital quantum batteries: storing energy and information in nanovacuum tube arrays." Complexity
.
15
(5): no data. doi:10.1002/cplx.20306. S2CID 6994736. - Lyon, D.; and others. (2013). "Dependence of the dielectric strength of nano-vacuum gaps on the gap size." IEEE Transactions on Dielectrics and Electrical Insulation
.
2
(4):1467–1471. doi:10.1109/TDEI.2013.6571470. S2CID 709782. - Calculated from fractional mass loss times the square of c.
- Calculated from the square of the fractional mass loss multiplied by c. Ball, Justin (2019). "Maximizing specific energy by deuterium multiplication". Thermonuclear reaction
.
59
(10): 106043. arXiv:1908.00834. Bibcode:2019NucFu..59j6043B. Doi:10.1088/1741-4326/ab394c. S2CID 199405246. - Calculated from the square of the fractional mass loss multiplied by c.
- ^ a b
"Calculation of the specific energy of nuclear fuel." whatisnuclear.com. Retrieved 2014-04-17. - ^ a b c
College of the Desert, “Module 1, Properties of Hydrogen,” Revision 0, December 2001. Properties of Hydrogen. Retrieved June 8, 2014. - Greenwood, Norman N.; Earnshaw, Alan (1997), Chemistry of the Elements (2nd ed) (p. 164)
- “Boron: a better energy carrier than hydrogen? (February 28, 2009).” Eagle.ca. Retrieved 2010-05-07.
- ^ a b c d
Envestra Limited. Natural gas Archived 2008-10-10 on the Wayback Machine. Retrieved October 5, 2008. - ^ a b c d e
IOR Energy. List of common conversion factors (engineering conversion factors). Retrieved October 5, 2008. - ^ a b c d e
Paul A. Kittle, Ph.D. "ALTERNATIVE DAILY COVER MATERIALS AND UNIT D - SELECTION TECHNIQUE" (PDF). Archived from the original (PDF) on 2008-05-27. Retrieved 2012-01-25. - "537.PDF" (PDF). June 1993. Retrieved 2012-01-25.
- Goffman, Evelyn (2003). Ehlert, Glenn (ed.). "Energy value of aviation fuel." Physics Fact Book
. Received 2019-07-28. - "Product Directory" (PDF). Air BP. pp. 11–13. Archived from the original (PDF) on 2011-06-08.
- Characteristics of stored and released petroleum products
(PDF), Petroleum Products Division - GN, p. 132, original archived (PDF) January 16, 2022, retrieved January 15, 2017 - Roman-Leshkov, Yuri; Barrett, Christopher J.; Liu, Zhen Y.; Dumesik, James A. (June 21, 2007). "Production of dimethylfuran for liquid fuels from biomass-derived carbohydrates." Nature
.
447
(7147):982–985. Bibcode:2007Natura.447..982R. Doi:10.1038/nature05923. PMID 17581580. S2CID 4366510. - Justin Lemire-Elmore (April 13, 2004). "Energy costs of electric and human-powered bicycles" (PDF). paragraph 5. Received 2009-02-26. a properly trained athlete has an efficiency of 22 to 26%
- Merue, Lauryn (2020). "Thermal Energy Storage in Silicon". doi:10.1016/j.renene.2019.06.036. Magazine citation required | log = (Help)
- Bossel, Ulf (July 2003). "The Physics of the Hydrogen Economy" (PDF). European fuel cell news. Archived from the original (PDF) on 2006-03-19. Retrieved 2019-04-06. Higher heating values are 22.7, 29.7 or 31.7 MJ/kg for methanol, ethanol and DME, respectively, while gasoline contains about 45 MJ/kg.
- "Dimethyl Ether (DME)" (PDF). European Biofuels Technology Platform
. 2013-11-18. Retrieved 2019-04-06. DME density and lower heating value were obtained from the table on the first page. - "Elite_bloc.indd" (PDF). Archived from the original (PDF) on 2011-07-15. Retrieved 2010-05-07.
- "Biomass Energy Foundation: Fuel Density." woodgas.com. Archived from the original on 2010-01-10. Retrieved 2010-05-07.
- "Bord na Mona, peat for energy" (PDF). Bnm.ie. Archived from the original (PDF) on 2007-11-19. Retrieved 2012-01-25.
- Justin Lemire-Elmore (April 13, 2004). "Energy Cost of Electric and Human Powered Bicycles" (PDF). Retrieved 2012-01-25.
- "energy buffers". Home.hccnet.nl. Retrieved 2010-05-07.
- Anne Wignall and Terry Wales. Chemistry Textbook 12, p. 138 Archived 2011-09-13 on the Wayback Machine. Pearson Education NZ ISBN 978-0-582-54974-6
- Mitchell, Robert R.; Betar M. Gallant; Carl W. Thompson; Yang Shao-Horn (2011). "Carbon nanofiber electrodes for high-energy rechargeable Li–O2 batteries". Energy and ecology
.
4
(8):2952–2958. Doi:10.1039/C1EE01496J. S2CID 96799565. - David E. Dirks. energy buffers. “household waste 8..11 MJ/kg”
- Lu, Gui-e; Chang, Wen-ping; Jiang, Jin-Yong; Du Shi-guo (May 2011). "Investigation of the energy density of a powder heat source." 2011 International Conference on Materials for Renewable Energy and the Environment
. IEEE: 1185–1187. doi:10.1109/ICMREE.2011.5930549. ISBN 978-1-61284-749-8. S2CID 36130191. - "Technical Bulletin on Zinc Air Batteries." Duracell. Archived from the original on 2009-01-27. Retrieved 2009-04-21.
- K. Nowlen, A.T. Mattick, A.P. Bruckner and A. Hertzberg, “High Efficiency Conversion Systems for Liquid Nitrogen Vehicles,” Society of Automotive Engineers, 1988.
- "Lithium-Ion Battery Review" (PDF). Panasonic. January 2007 Archived (PDF) from the original November 7, 2011
- "Panasonic NCR18650B" (PDF). Archived from the original (PDF) on 07/22/2015.
- [44][45]
- "Duracell Ultra Power AA Test." lygte-info.dk
. Received 2019-02-16. - “Energizer EN91 AA Alkaline Battery Data Sheet” (PDF). Retrieved 2016-01-10.
- ^ a b
"Test GP ReCyko + AA 2700mAh (green)".
lygte-info.dk
. Received 2019-02-16. - ^ a b
"Maxwell Supercapacitor Comparison" (PDF). Retrieved 2016-01-10. - ^ a b
“Technical description of Nesscap ESHSP series supercapacitors” (PDF). Archived from the original (PDF) on 2016-03-29. Retrieved 2016-01-10. - ^ a b
“Cooper PowerStor XL60 Series Supercapacitor Data Sheet” (PDF). Retrieved 2016-01-10. - ^ a b
“Technical Description of Kemet S301 Series Supercapacitors” (PDF). Archived from the original (PDF) on 2016-03-04. Retrieved 2016-01-10. - ^ a b
“Technical Description of Nichicon JJD Series Supercapacitor” (PDF). Retrieved 2016-01-10. - ^ a b
"Skelcap high energy ultracapacitor" (PDF).
Skeletal technologies
. Archived from the original (PDF) on April 2, 2016. Retrieved October 13, 2015. - ^ a b
"TECHNICAL DESCRIPTION OF ULTRACAPACITOR CELL 3.0V 3400F BCAP3400 P300 K04/05" (PDF). Received 2020-01-12. - "Hydropower". www.mpoweruk.com
. Woodbank Communications Ltd. Retrieved April 13, 2022. - “2.1 Electricity, unloading, relations between managers | River Engineering and Restoration at OSU | Oregon State University." river.bee.oregonstate.edu
. Retrieved April 13, 2022. Let ε = 0.85, which means an efficiency rating of 85%, typical of an older power plant. - ^ a b
“Technical description of Vishay STE series tantalum capacitors” (PDF). Retrieved 2016-01-10. - "Technical Data of Nichicon TVX Aluminum Electrolytic Capacitors" (PDF). Retrieved 2016-01-10.
- “Technical Description of Nichicon LGU Aluminum Electrolytic Capacitors” (PDF). Retrieved 2016-01-10.
- ^ a b c
“How much energy can be stored in an elastic band?”
Wired
. ISSN 1059-1028. Received 2020-01-21. - ^ a b c
"MatWeb - Internet resource with information about materials."
www.matweb.com
. Received 2019-12-15. - PubChem. "Acetal". pubchem.ncbi.nlm.nih.gov
. Retrieved 2019-12-12. - ^ a b c d f g h i j k l m p o p q r s t u v
“Young’s modulus - tensile strength and yield strength for ordinary materials.
” www.engineeringtoolbox.com
. Retrieved 2019-12-12. - ^ a b c d f g h i Brush
Wellman Alloy Products.
"Elasticity" (PDF). Tech tidbits
. Retrieved December 15, 2022. - “C17200 Alloy Specifications | E. Jordan Brookes Company.” www.ejbmetals.com
. Received 2019-12-15. - "Information and properties of polycarbonate." www.polymerprocessing.com
. Retrieved 2019-12-12. - "ASM Technical Data Sheet." asm.matweb.com
. Received 2019-12-15. - Sutherland, Karen; Martin, Monica (2004). Ehlert, Glenn (ed.). "Density of steel." Physics Fact Book
. Retrieved 2020-06-18. - "Wood species - moisture content and weight." www.engineeringtoolbox.com
. Retrieved 2019-12-12. - ^ a b c
"Mild/low carbon steel AISI 1018".
AZoM.com
. 2012-06-28. Received 2020-01-22. - "ASM Technical Data Sheet." asm.matweb.com
. Retrieved 2019-12-12. - ^ a b c
"American Eastern White Pine."
www.matweb.com
. Received 2019-12-15. - ^ a b
"Mass, weight, density or specific gravity of various metals."
www.simetric.co.uk
. Retrieved 2019-12-12. - “Physical properties of glass | Saint Gobain Building Glass UK.” uk.saint-gobain-building-glass.com
. Retrieved 2019-12-12. - ^ a b
"Battery Energy Tables". Archived from the original on 2011-12-04. - "Battery capacity is 18650."
- "Supply of uranium." world-nuclear.org. 2014-10-08. Retrieved 2015-06-13.
- "Cohen Facts". formal.stanford.edu. 2007-01-26. Archived from the original on 2007-04-10. Retrieved 2010-05-07.
- “U.S. Energy Information Administration (EIA) Annual Energy Review.” Eia.doe.gov. 2009-06-26. Archived from the original on 2010-05-06. Retrieved 2010-05-07.
- Parravicini, G. (2018). "Thermodynamic potentials in anisotropic and nonlinear dielectrics". Physica
B.
541
: 54–60. Bibcode:2018PhyB..541 … 54P. doi:10.1016/j.physb.2018.04.029. - "Terminology". Regenerative laser therapy
.
external links
- "Aviation fuel". Energy, Technology and Environment
Ed. Attilio Bisio. Vol. 1. New York: John Wiley and Sons, Inc., 1995. 257–259. - "Fuels of the Future for Cars and Trucks" - Dr. James J. Eberhard - Energy Efficiency and Renewable Energy, US Department of Energy - 2002 Diesel Emissions Reduction (DEER) Workshop San Diego, CA - August 25-29 2002
- "Thermal Values of Various Fuels - World Nuclear Association." www.world-nuclear.org
. Retrieved November 4, 2022. - "Energy and Energy Types - Springer" (PDF). Retrieved November 4, 2018.