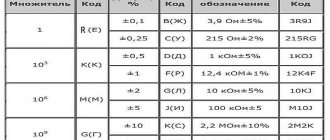
The online calculator determines the calculated permissible stresses σ depending on the design temperature for various grades of materials of the following types: carbon steel, chromium steel, austenitic steel, austenitic-ferritic steel, aluminum and its alloys, copper and its alloys, titanium and its alloys according GOST-52857.1-2007 [1].
| Initial data: | |
| Estimated ambient temperature T, °C | |
| Material type | |
| Material grade | |
| Solution: | |
| Allowable stress of the material [σ], MPa | determination of permissible stress |
Assistance for the development of the premierdevelopment.ru project
Send mail and we will know that we are moving in the right direction. Thank you for stopping by!
I. Calculation method:
Allowable stresses were determined according to GOST-52857.1-2007 [1].
for carbon and low alloy steels
St3, 09G2S, 16GS, 20, 20K, 10, 10G2, 09G2, 17GS, 17G1S, 10G2S1:
- At design temperatures below 20°C, the permissible stresses are taken to be the same as at 20°C, subject to the permissible use of the material at a given temperature.
- For intermediate design wall temperatures, the permissible stress is determined by linear interpolation with rounding the results down to 0.5 MPa.
- For steel grade 20 at Re/20e/20/220.
- For steel grade 10G2 at Rр0.2/20р0.2/20/270.
- For steel grades 09G2S, 16GS, strength classes 265 and 296 according to GOST 19281, the permissible stresses, regardless of the sheet thickness, are determined for thicknesses over 32 mm.
- The permissible stresses located below the horizontal line are valid for a service life of no more than 105 hours. For a design service life of up to 2*105 hours, the permissible stress located below the horizontal line is multiplied by the coefficient: for carbon steel by 0.8; for manganese steel by 0.85 at temperatures <450 °C and by 0.8 at temperatures from 450 °C to 500 °C inclusive.
for heat-resistant chromium steels
12XM, 12MX, 15XM, 15X5M, 15X5M-U:
- At design temperatures below 20 °C, the permissible stresses are taken to be the same as at 20 °C, subject to the permissible use of the material at a given temperature.
- For intermediate design wall temperatures, the permissible stress is determined by linear interpolation with rounding the results down to 0.5 MPa.
- The permissible stresses located below the horizontal line are valid for a service life of 105 hours. For a design service life of up to 2 * 105 hours, the permissible stress located below the horizontal line is multiplied by a factor of 0.85.
What is this indicator?
The ultimate stress of a material is the maximum tensile force that must be applied to its cross-sectional area that it can resist until it completely breaks or fractures. A simple calculation formula looks like this: voltage equals force divided by area. It shows that the larger the area, the less force needs to be applied. The same is true vice versa. The smaller the cross-section of the workpiece, the more force it will take to break it.
However, the stiffness indicators of different materials are not the same. Some are fragile, others are elastic. The maximum permissible stress for each is determined using mechanical tests. The result is considered achieved when external signs of integrity damage appear on the surface of the sample. They can be expressed in the form of destruction or fracture. For the latter, the term “yield strength” is used. The first speaks of fragility, the second - of plasticity.
Both concepts are associated with the limiting stress at which the strength of the material is broken. Let's take a closer look at how these two concepts are differentiated.
for heat-resistant, heat-resistant and corrosion-resistant austenitic steels
03X21H21M4GB, 03X18H11, 03X17H14M3, 08X18H10T, 08X18H12T, 08X17H13M2T, 08X17H15M3T, 12X18H10T, 12X18H12T, 10X17H13M2T, 10X 17H13M3T, 10X14G14H4:
- At design temperatures below 20 °C, the permissible stresses are taken to be the same as at 20 °C, subject to the permissible use of the material at a given temperature.
- For intermediate design wall temperatures, the permissible stress is determined by interpolating the two closest values indicated in the table, with the results rounded down to the nearest 0.5 MPa.
- For forgings made of steel grades 12Х18Н10Т, 10Х17Н13M2T, 10Х17Н13М3Т, the permissible stresses at temperatures up to 550 °C are multiplied by 0.83.
- For long rolled steel grades 12Х18Н10Т, 10Х17Н13M2T, 10Х17Н13М3Т, permissible stresses at temperatures up to 550 °С are multiplied by the ratio (R*p0.2/20) / 240. (R*p0.2/20 - the yield strength of the long rolled material is determined by GOST 5949).
- For forgings and long products made of steel grade 08X18H10T, the permissible stresses at temperatures up to 550 °C are multiplied by 0.95.
- For forgings made of steel grade 03X17H14M3, the permissible stresses are multiplied by 0.9.
- For forgings made of steel grade 03X18H11, the permissible stresses are multiplied by 0.9; for long products made of steel grade 03X18H11, the permissible stresses are multiplied by 0.8.
- For pipes made of steel grade 03Х21Н21М4ГБ (ZI-35), the permissible stresses are multiplied by 0.88.
- For forgings made of steel grade 03Х21Н21М4ГБ (ZI-35), the permissible stresses are multiplied by the ratio (R*p0.2/20) / 250. (R*p0.2/20 is the yield strength of the forging material, determined according to GOST 25054).
- The permissible stresses located below the horizontal line are valid for a service life of no more than 105 hours.
For a design service life of up to 2*105 hours, the permissible voltage located below the horizontal line is multiplied by a factor of 0.9 at temperatures <600 °C and by a factor of 0.8 at temperatures from 600 °C to 700 °C inclusive.
Stress calculation
The bending moment Mx arising in cross sections during pure straight bending is the resultant moment of internal normal forces distributed over the section and causing normal stresses at the points of the section.
The law of distribution of normal stresses along the height of the section is expressed by the formula: where: M is the bending moment acting in the section under consideration relative to its neutral line X; Ix is the axial moment of inertia of the beam cross section relative to the neutral axis; y is the distance from the neutral axis to the point at which the voltage is determined.
The neutral axis during bending passes through the center of gravity of the cross section.
According to the above formula, normal stresses along the height of the section change according to a linear law.
The stresses at the upper and lower edges of the section have the greatest values.
For example, for a section symmetrical about the neutral axis, where y1=y2=h/2:
The stresses at the vertical extreme points (points 1 and 2) are equal in magnitude, but opposite in sign. For an asymmetrical section
stresses are determined separately for the lower point 1 and the upper point 2: where: WX is the axial moment of resistance of a symmetrical section; WX(1) and WX(2) are axial moments of resistance of an asymmetrical section for the lower and upper layers of the beam.
It is recommended to determine the signs of normal stresses when calculating them according to their physical meaning, depending on whether the layers of the beam under consideration are stretched or compressed.
for titanium and its alloys
VT1-0, OT4-0, AT3, VT1-00:
- At design temperatures below 20 °C, the permissible stresses are taken to be the same as at 20 °C, subject to the permissibility of using the material at a given temperature.
- For forgings and rods, the permissible stresses are multiplied by 0.8.
II. Definitions and notations:
Re/20 - minimum value of the yield strength at a temperature of 20 °C, MPa; Rр0.2/20 - minimum value of the conditional yield strength at a permanent elongation of 0.2% at a temperature of 20 °C, MPa. permissible stress - the highest stress that can be allowed in a structure, subject to its safe, reliable and durable operation. The value of the permissible stress is established by dividing the tensile strength, yield strength, etc. by a value greater than one, called the safety factor. design temperature - the temperature of the wall of equipment or a pipeline, equal to the maximum arithmetic mean value of the temperatures on its outer and inner surfaces in one section under normal operating conditions (for parts of nuclear reactor vessels, the design temperature is determined taking into account internal heat releases as the average integral value of the temperature distribution over the thickness of the vessel wall ( PNAE G-7-002-86, clause 2.2; PNAE G-7-008-89, appendix 1).
Design temperature
- [1], clause 5.1. The design temperature is used to determine the physical and mechanical characteristics of the material and permissible stresses, as well as when calculating strength taking into account temperature effects.
- [1], clause 5.2. The design temperature is determined on the basis of thermal calculations or test results, or operating experience of similar vessels.
- The highest wall temperature is taken as the design temperature of the wall of the vessel or apparatus. At temperatures below 20 °C, a temperature of 20 °C is taken as the design temperature when determining permissible stresses.
- [1], clause 5.3. If it is impossible to carry out thermal calculations or measurements and if during operation the wall temperature rises to the temperature of the medium in contact with the wall, then the highest temperature of the medium, but not lower than 20 °C, should be taken as the design temperature.
- When heating with an open flame, exhaust gases or electric heaters, the design temperature is taken equal to the ambient temperature increased by 20 °C for closed heating and by 50 °C for direct heating, unless more accurate data are available.
- [1], clause 5.4. If a vessel or apparatus is operated under several different loading modes or different elements of the apparatus operate under different conditions, for each mode its own design temperature can be determined (GOST-52857.1-2007, clause 5).
III. Note:
The source data block is highlighted in yellow, the intermediate calculation block is highlighted in blue, and the solution block is highlighted in green.
Limit stresses. Limit and permissible stresses
Initial data:
| Estimated ambient temperature | T= | ºС |
| Material type | carbon steel chromium steel austenitic steel austenitic-ferritic steel aluminum and its alloys copper and its alloys titanium and its alloys | |
| Material grade | St3 (S up to 20 mm) St3 (S over 20 mm) 09G2S (S up to 32 mm) 09G2S (S over 32 mm) 16GS (S up to 32 mm) 16GS (S over 32 mm) 20 20K 10 10G2 09G2 17GS 17G1S 10G2S1 |
Definition of auxiliary variables:
Permissible stress
...permissible stress is being determined...
MPa - standard value
Calculation method:
1. Allowable stresses were determined in accordance with GOST-52857.1-2007.
Definitions:
Allowable voltages:
Allowable stress is the highest stress that can be allowed in a structure under the condition of its safe, reliable and durable operation. The value of the permissible stress is established by dividing the tensile strength, yield strength, etc. by a value greater than one, called the safety factor.
Design temperature
Design temperature - the temperature of the wall of equipment or a pipeline, equal to the maximum arithmetic mean value of the temperatures on its outer and inner surfaces in one section under normal operating conditions (for parts of nuclear reactor vessels, the design temperature is determined taking into account internal heat releases as the average integral value of the temperature distribution over the thickness of the vessel wall ( PNAE G-7-002-86, clause 2.2; PNAE G-7-008-89, appendix 1)
, item 5 Design temperature
,Clause 5.1. The design temperature is used to determine the physical and mechanical characteristics of the material and permissible stresses, as well as when calculating strength taking into account temperature effects. ,Clause 5.2. The design temperature is determined on the basis of thermal calculations or test results, or operating experience of similar vessels. The highest wall temperature is taken as the design temperature of the wall of the vessel or apparatus. At temperatures below 20 °C, a temperature of 20 °C is taken as the design temperature when determining permissible stresses. ,section 5.3. If it is impossible to carry out thermal calculations or measurements and if during operation the wall temperature rises to the temperature of the medium in contact with the wall, then the highest temperature of the medium, but not lower than 20 °C, should be taken as the design temperature. When heating with an open flame, exhaust gases or electric heaters, the design temperature is taken equal to the ambient temperature increased by 20 °C for closed heating and by 50 °C for direct heating, unless more accurate data are available. ,section 5.4. If a vessel or apparatus is operated under several different loading modes or different elements of the apparatus operate under different conditions, its own design temperature can be determined for each mode. (GOST-52857.1-2007, clause 5)
Note:
for carbon and low-alloy steels St3, 09G2S, 16GS, 20, 20K, 10, 10G2, 09G2, 17GS, 17G1S, 10G2S1:
1. At design temperatures below 20°C, the permissible stresses are taken to be the same as at 20°C, subject to the permissible use of the material at a given temperature.
3. For steel grade 20 at R e/20 4. For steel grade 10G2 at R р0.2/20 5. For steel grades 09G2S, 16GS strength classes 265 and 296 according to GOST 19281, the permissible stresses, regardless of sheet thickness, are determined for thicknesses over 32 mm. 6. The permissible stresses located below the horizontal line are valid for a service life of no more than 10 5 hours. For a design service life of up to 2 * 10 5 hours, the permissible stress located below the horizontal line is multiplied by the coefficient: for carbon steel by 0.8; for manganese steel by 0.85 at a temperature
for heat-resistant chromium steels 12ХМ, 12МХ, 15ХМ, 15Х5М, 15Х5М-У:
1. At design temperatures below 20 °C, the permissible stresses are taken to be the same as at 20 °C, subject to the permissible use of the material at a given temperature. 2. For intermediate design wall temperatures, the permissible stress is determined by linear interpolation with rounding the results to 0.5 MPa towards a lower value. 3. The permissible stresses located below the horizontal line are valid for a service life of 10 5 hours. For a design service life of up to 2 * 10 5 hours, the permissible stress located below the horizontal line is multiplied by a factor of 0.85.
for heat-resistant, heat-resistant and corrosion-resistant steels of austenitic class 03X21N21M4GB, 03X18H11, 03X17H14M3, 08X18H10T, 08X18H12T, 08X17H13M2T, 08X17H15M3T, 12X18H10T, 12 X18H12T, 10X17H13M2T, 10X17H13M3T, 10Х14Г14Н4:
2. For intermediate design wall temperatures, the permissible stress is determined by interpolating the two closest values indicated in the table, with the results rounded down to 0.5 MPa towards the lower value. 3. For forgings made of steel grades 12Х18Н10Т, 10Х17Н13M2T, 10Х17Н13М3Т, permissible stresses at temperatures up to 550 °С are multiplied by 0.83. 4. For long rolled steel grades 12Х18Н10Т, 10Х17Н13M2T, 10Х17Н13М3Т, permissible stresses at temperatures up to 550 °С are multiplied by the ratio (R* p0.2/20) / 240 (R* p0.2/20 - the yield strength of the long rolled material is determined according to GOST 5949). 5. For forgings and long products made of steel grade 08X18H10T, the permissible stresses at temperatures up to 550 °C are multiplied by 0.95. 6. For forgings made of steel grade 03X17H14M3, the permissible stresses are multiplied by 0.9. 7. For forgings made of steel grade 03X18H11, the permissible stresses are multiplied by 0.9; for long products made of steel grade 03X18H11, the permissible stresses are multiplied by 0.8. 8. For pipes made of steel grade 03Х21Н21М4ГБ (ZI-35), the permissible stresses are multiplied by 0.88. 9. For forgings made of steel grade 03Х21Н21М4ГБ (ZI-35), the permissible stresses are multiplied by the ratio (R* p0.2/20) / 250 (R* p0.2/20 is the yield strength of the forging material, determined according to GOST 25054). 10. Permissible stresses located below the horizontal line are valid for a service life of no more than 10 5 hours. For a design service life of up to 2 * 10 5 hours, the permissible stress located below the horizontal line is multiplied by a factor of 0.9 at temperature
for heat-resistant, heat-resistant and corrosion-resistant steels of austenitic and austenitic-ferritic class 08Kh18G8N2T (KO-3), 07Kh13AG20 (ChS-46), 02Kh8N22S6 (EP-794), 15Kh18N12S4TYu (EI-654), 06KhN28MDT, 03KhN28 MDT, 08Х22Н6Т, 08Х21Н6М2Т : 1. At design temperatures below 20 °C, the permissible stresses are taken to be the same as at 20 °C, subject to the permissible use of the material at a given temperature. 2. For intermediate design wall temperatures, the permissible stress is determined by interpolating the two closest values indicated in this table, rounded to the nearest 0.5 MPa towards the lower value.
for aluminum and its alloys A85M, A8M, ADM, AD0M, AD1M, AMtsSM, AM-2M, AM-3M, AM-5M, AM-6M:
1. Allowable stresses are given for aluminum and its alloys in the annealed state. 2. Allowable stresses are given for thicknesses of sheets and plates of aluminum grades A85M, A8M no more than 30 mm, other grades - no more than 60 mm.
for copper and its alloys M2, M3, M3r, L63, LS59-1, LO62-1, LZhMts 59-1-1:
1. Allowable stresses are given for copper and its alloys in the annealed state. 2. Allowable stresses are given for sheet thicknesses from 3 to 10 mm. 3. For intermediate values of the calculated wall temperatures, the permissible stresses are determined by linear interpolation with rounding the results to 0.1 MPa towards the lower value.
for titanium and its alloys VT1-0, OT4-0, AT3, VT1-00:
1. At design temperatures below 20 °C, the permissible stresses are taken to be the same as at 20 °C, provided that the use of the material is permissible at a given temperature. 2. For forgings and rods, the permissible stresses are multiplied by 0.8.
Abbreviations and designations:
R e/20—minimum value of the yield strength at a temperature of 20 °C, MPa; R р0.2/20 - minimum value of the proof yield strength at permanent elongation 0.2% at a temperature of 20 °C, MPa;
Ultimate voltage
They consider the stress at which a dangerous condition occurs in a material (fracture or dangerous deformation).
For plastic
materials, the ultimate stress is considered to be the
because the resulting plastic deformations do not disappear after removing the load:
For fragile
materials where there are no plastic deformations, and fracture occurs of the brittle type (no necking is formed), the ultimate stress is taken to be
the tensile strength:
For plastic-brittle materials
materials, the ultimate stress is considered to be the stress corresponding to a maximum deformation of 0.2% (one hundred.2):
Allowable voltage
- the maximum voltage at which the material should work normally.
The permissible stresses are obtained according to the limit values, taking into account the safety factor:
where [σ] is the permissible stress; s
— safety factor; [s] is the permissible safety factor.
Note.
It is customary to indicate the permissible value of a quantity in square brackets.
Allowable safety factor
depends on the quality of the material, operating conditions of the part, purpose of the part, accuracy of processing and calculation, etc.
It can range from 1.25 for simple parts to 12.5 for complex parts operating under variable loads under conditions of shock and vibration.
Features of the behavior of materials during compression tests:
1. Plastic materials work almost equally under tension and compression. The mechanical characteristics in tension and compression are the same.
2. Brittle materials usually have greater compressive strength than tensile strength: σ vr
If the permissible stress in tension and compression is different, they are designated [σ р ] (tension), [σ с ] (compression).
Tensile and compressive strength calculations
Strength calculations are carried out according to strength conditions - inequalities, the fulfillment of which guarantees the strength of the part under given conditions.
To ensure strength, the design stress should not exceed the permissible stress:
Design voltage a
depends
on the load and
cross-sectional dimensions, permissible only
on the material of the part
and operating conditions.
There are three types of strength calculations.
1.
Design calculation
- the design scheme and loads are specified;
the material or dimensions of the part are selected:
Determination of cross-sectional dimensions:
Selection of material
Based on the value of σ, it is possible to select the grade of material.
2. Check calculation -
the loads, material, dimensions of the part are known;
it is necessary to check whether the strength is ensured.
Inequality is checked
3. Determination of load capacity
(maximum load):
Examples of problem solving
The straight beam is stretched with a force of 150 kN (Fig. 22.6), the material is steel σ t = 570 MPa, σ b = 720 MPa, safety factor [s] = 1.5. Determine the cross-sectional dimensions of the beam.
Solution
1. Strength condition:
2. The required cross-sectional area is determined by the relation
3. The permissible stress for the material is calculated from the specified mechanical characteristics. The presence of a yield point means that the material is plastic.
4. We determine the required cross-sectional area of the beam and select dimensions for two cases.
The cross section is a circle, we determine the diameter.
We round the resulting value up d =
25 mm, A = 4.91 cm 2.
Section - equal angle angle No. 5 according to GOST 8509-86.
The closest cross-sectional area of the corner is A = 4.29 cm 2 (d = 5 mm). 4.91 > 4.29 (Appendix 1).
Test questions and assignments
1. What phenomenon is called fluidity?
2. What is a “neck”, at what point on the stretch diagram does it form?
3. Why are the mechanical characteristics obtained during testing conditional?
4. List the strength characteristics.
5. List the characteristics of plasticity.
6. What is the difference between an automatically drawn stretch diagram and a given stretch diagram?
7. Which mechanical characteristic is chosen as the limiting stress for ductile and brittle materials?
8. What is the difference between ultimate and permissible stress?
9. Write down the condition for tensile and compressive strength. Are the strength conditions different for tensile and compressive calculations?
Answer the test questions.
To determine permissible stresses in mechanical engineering, the following basic methods are used. 1. A differentiated safety factor is found as the product of a number of partial coefficients that take into account the reliability of the material, the degree of responsibility of the part, the accuracy of the calculation formulas and the acting forces and other factors that determine the operating conditions of the parts. 2. Tabular - permissible voltages are taken according to standards, systematized in the form of tables (Tables 1 - 7). This method is less accurate, but is the simplest and most convenient for practical use in design and testing strength calculations.
In the work of design bureaus and in the calculations of machine parts, both differentiated and tabular methods, as well as their combination. In table 4 – 6 show the permissible stresses for non-standard cast parts for which special calculation methods and the corresponding permissible stresses have not been developed. Typical parts (for example, gears and worm wheels, pulleys) should be calculated using the methods given in the corresponding section of the reference book or specialized literature.
The permissible stresses given are intended for approximate calculations only for basic loads. For more accurate calculations taking into account additional loads (for example, dynamic), the table values should be increased by 20 - 30%.
Allowable stresses are given without taking into account the stress concentration and dimensions of the part, calculated for smooth polished steel samples with a diameter of 6-12 mm and for untreated round cast iron castings with a diameter of 30 mm. When determining the highest stresses in the part being calculated, it is necessary to multiply the nominal stresses σ nom and τ nom by the concentration factor k σ or k τ:
1. Allowable stresses* for carbon steels of ordinary quality in the hot-rolled state
2. Mechanical properties and permissible stresses of high-quality carbon structural steels
3. Mechanical properties and permissible stresses of alloyed structural steels
4. Mechanical properties and permissible stresses for castings made of carbon and alloy steels
5. Mechanical properties and permissible stresses for gray cast iron castings
6. Mechanical properties and permissible stresses for ductile iron castings
For ductile (non-hardened) steels
for static stresses (I type of load), the concentration coefficient is not taken into account.
For homogeneous steels (σ in > 1300 MPa, as well as in the case of their operation at low temperatures), the concentration coefficient, in the presence of stress concentration, is introduced into the calculation for loads of I
(k > 1). For ductile steels under variable loads and in the presence of stress concentrations, these stresses must be taken into account.
For cast iron
in most cases, the stress concentration coefficient is approximately equal to unity for all types of loads (I – III). When calculating strength to take into account the dimensions of the part, the given tabulated permissible stresses for cast parts should be multiplied by a scale factor equal to 1.4 ... 5.
Approximate empirical dependences of endurance limits for cases of loading with a symmetrical cycle:
for carbon steels:
– during bending,
σ -1 = (0.40÷0.46)σ in
;
σ -1р =(0.65÷0.75)σ -1
;
– in torsion, τ -1 =(0.55÷0.65)σ -1
;
for alloy steels:
– during bending,
σ -1 = (0.45÷0.55)σ in
;
– in tension or compression, σ -1р = (0.70÷0.90)σ -1
;
– in torsion, τ -1 =(0.50÷0.65)σ -1
;
for steel casting:
– during bending,
σ -1 = (0.35÷0.45)σ in
;
– in tension or compression, σ -1р = (0.65÷0.75)σ -1
;
– in torsion, τ -1 =(0.55÷0.65)σ -1
.
Mechanical properties and permissible stresses of anti-friction cast iron:
– ultimate bending strength 250 – 300 MPa, – permissible bending stress: 95 MPa for I; 70 MPa – II: 45 MPa – III, where I. II, III are designations of types of load, see table. 1.
Approximate permissible stresses for non-ferrous metals in tension and compression. MPa:
– 30…110 – for copper; – 60…130 – brass; – 50…110 – bronze; – 25…70 – aluminum; – 70…140 – duralumin.
The safety factor of any structural element is equal to the ratio of the maximum load, which causes a loss of strength of the element, to the load, which creates the permissible stress. In this case, the loss of strength means not only the destruction of the element, but also the appearance of residual deformations in it. Therefore, for a structural element made of a plastic material, the ultimate stress is the yield limit. In most cases, operating stresses in structural elements are proportional to the load, and therefore the safety factor is defined as the ratio of the ultimate strength to the permissible stress (safety factor for ultimate strength). So, if the tensile strength of structural steel is 540 MPa, and the permissible stress is 180 MPa, then the safety factor is 3.
Allowable (allowable) stress is the stress value that is considered extremely acceptable when calculating the cross-sectional dimensions of an element, calculated for a given load. We can talk about permissible tensile, compressive and shear stresses. Permissible stresses are either proposed by a competent authority (say, the bridge department of the railway department), or selected by a designer aware of the properties of the material and the conditions of its use. The permissible stress limits the maximum operating voltage of the structure.
In strength of materials, much attention is paid to the derivation of relationships between given loads, the dimensions and shape of the element supporting the load or supporting them, and the stresses arising in certain sections of the structural element. As a rule, the purpose of the calculations is to find the required dimensions of the element at which the maximum operating voltage in it will not exceed the permissible one.
When designing structures, the goal is to create a structure that, while being reliable, at the same time would be extremely light and economical. Reliability is ensured by the fact that each element is provided with such dimensions that the maximum operating voltage in it will be to a certain extent less than the voltage that causes a loss of strength for this element. Loss of strength does not necessarily mean destruction. A machine or building structure is considered to have failed when it cannot perform its function satisfactorily. A part made of a plastic material, as a rule, loses strength when the stress in it reaches the yield point, since due to too much deformation of the part, the machine or structure ceases to meet its intended purpose. If the part is made of brittle material, then it is almost not deformed, and its loss of strength coincides with its destruction.
1.4.10. For elements of vessels and apparatus that are not calculated based on maximum loads (for example, flange connections), the permissible stresses must be determined in accordance with the relevant regulatory and technical documentation approved in the prescribed manner.
The creep limit is used to determine the permissible stress in cases where there is no data on the limits of long-term strength or, due to operating conditions, it is necessary to limit the amount of deformation (displacement).
4.3 The basis for strength calculation methods for most vessel elements is the calculation method based on maximum loads. For convenience of calculation, safety factors up to ultimate loads are taken into account when determining permissible stresses. For individual elements (for example, flange connections) or load conditions, for example under alternating loads, the calculation is carried out according to the permissible stresses.
Since parts and structures as a whole must operate safely even under these unfavorable conditions, certain precautions must be taken. For this purpose, the stresses that ensure trouble-free operation (operation) of a machine or any other structure must be lower than those limiting stresses at which destruction or plastic deformation can occur.
Carbon and low-alloy steels are widely used in the construction of cars. For the manufacture of the main load-bearing elements of cars (bogie frames, spinal and pivot beams, frame and body skin), low-alloy steel grade 09G2D, which has increased strength and corrosion resistance, is most used. During the construction of new freight cars in the tenth five-year plan, low-alloy steels 10KhNDP and 10G25D will be used.
Permissible stresses and safety factors for threaded connections are given in tables 1.2 and 1.3. They take into account the accuracy of the calculation formulas, the nature of the load, the quality of the connection installation (controlled or uncontrolled tightening), etc.
When choosing a material, take into account operating conditions (temperature, corrosion, etc.), the value and nature of the load (static or variable), manufacturing method and production volume. For example, standard general-purpose fasteners are made from low- and medium-carbon steels such as steel 10 ... steel 35. These inexpensive steels allow large quantities of bolts, screws and nuts to be produced by cold heading or stamping and then rolling threads. Alloy steels 35Х, 30ХГСА are used for highly loaded parts under variable and shock loads, at high temperatures, in aggressive environments, etc.
In cases where an increase in the mass of the structure associated with an increase in the diameter of the bolts is unjustified (for example, aircraft construction), controlled tightening is used. The possibility of significantly increasing the static load of bolts made of steel 20 with controlled tightening is shown in Table 1.4.
| To determine permissible stresses in mechanical engineering, the following basic methods are used. 1. A differentiated safety factor is found as the product of a number of partial coefficients that take into account the reliability of the material, the degree of responsibility of the part, the accuracy of the calculation formulas and the acting forces and other factors that determine the operating conditions of the parts. 2. Tabular - permissible stresses are taken according to standards, systematized in the form of tables (Tables 1 - 7). This method is less accurate, but is the simplest and most convenient for practical use in design and testing strength calculations. In the work of design bureaus and in the calculations of machine parts, both differentiated and tabular methods, as well as their combination. In table 4 - 6 show the permissible stresses for non-standard cast parts for which special calculation methods and the corresponding permissible stresses have not been developed. Typical parts (for example, gears and worm wheels, pulleys) should be calculated using the methods given in the corresponding section of the reference book or specialized literature. The permissible stresses given are intended for approximate calculations only for basic loads. For more accurate calculations taking into account additional loads (for example, dynamic), the table values should be increased by 20 - 30%. Allowable stresses are given without taking into account the stress concentration and dimensions of the part, calculated for smooth polished steel samples with a diameter of 6-12 mm and for untreated round cast iron castings with a diameter of 30 mm. When determining the highest stresses in the part being calculated, it is necessary to multiply the nominal stresses σ nom and τ nom by the concentration factor k σ or k τ: 1. Allowable stresses* for carbon steels of ordinary quality in the hot-rolled state
* Gorsky A.I.. Ivanov-Emin E.B.. Karenovsky A.I. Determination of permissible stresses in strength calculations. 3. Mechanical properties and permissible stresses of alloyed structural steels 4. Mechanical properties and permissible stresses for castings made of carbon and alloy steels 5. Mechanical properties and permissible stresses for gray cast iron castings 6. Mechanical properties and permissible stresses for ductile iron castings 7. Permissible stresses for plastic parts For ductile (non-hardened) steels for static stresses (I type of load), the concentration coefficient is not taken into account. For cast iron in most cases, the stress concentration coefficient is approximately equal to unity for all types of loads (I - III). When calculating strength to take into account the dimensions of the part, the given tabulated permissible stresses for cast parts should be multiplied by a scale factor equal to 1.4 ... 5. Approximate empirical dependences of endurance limits for cases of loading with a symmetrical cycle: for carbon steels: - during bending, for alloy steels: - during bending, for steel casting: - during bending, Mechanical properties and permissible stresses of anti-friction cast iron: — ultimate bending strength 250 ÷ 300 MPa, — permissible bending stress: 95 MPa for I; 70 MPa - II: 45 MPa - III, where I. II, III are designations of types of load, see table. 1. Approximate permissible stresses for non-ferrous metals in tension and compression. MPa: - 30...110 - for copper; - 60...130 - brass; - 50...110 - bronze; - 25...70 - aluminum; - 70...140 - duralumin. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||