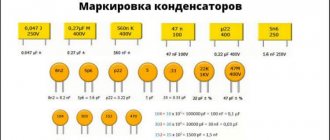
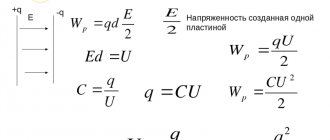Capacitors
The ability to store charge is a useful thing, which is why people came up with capacitors. These are devices that help to use the electrical capacitance of conductors for practical purposes.
A capacitor consists of two or more conducting plates (plates) separated by a dielectric. An electric field is formed between the conducting plates, all lines of force of which go from one plate to another.
Charging a capacitor is the process of accumulating charge on its two plates. The charges on them are equal in magnitude and opposite in sign.
The electrical capacity of a capacitor is measured by the ratio of the charge on one of the plates to the potential difference between the plates:
| Capacitance of the capacitor C = q/U C - electrical capacity [F] q —electric charge [C] U - voltage (potential difference) [V] |
According to the law of conservation of charge, if the plates of a charged capacitor are connected by a conductor, then the charges are neutralized, passing from one plate to another. This is how the capacitor discharges .
Any capacitor has a voltage limit. If it turns out to be too large, then dielectric breakdown , that is, discharge will occur directly through the dielectric. Such a capacitor will no longer work.
Formula
The capacitor charge current is found using the formula presented below. It is measured in farads, which is equal to a coulomb or volt.
Formula for finding the charge of a capacitor
In general, this is an element of the electrical network that accumulates and stores voltage in it. It comes in different types and sizes, for example, electrolytic, ceramic and tantalum. It consists mainly of several conductive plates with a dielectric. Its capacity depends on the size of the dielectric and the filler between the plates. Charges using electricity. The capacitor charge current can be determined using measuring instruments and a formula.
Read also: Strong or weak acid, how to tell?
Capacitor energy
A capacitor, like any system of charged bodies, has energy. To charge a capacitor, work must be done to separate negative and positive charges. According to the law of conservation of energy, this work will be exactly equal to the energy of the capacitor.
It is not difficult to prove that a charged capacitor has energy. To do this, you will need an electrical circuit containing an incandescent lamp and a capacitor. When the capacitor discharges, the lamp will flash - this will mean that the energy of the capacitor has been converted into heat and light energy.
To derive the formula for the energy of a flat capacitor, we need the formula for the energy of the electrostatic field.
| Electrostatic field energy Wp = qEd Wp – electrostatic field energy [J] q —electric charge [C] E – electric field strength [V/m] d —distance from charge [m] |
In the case of a capacitor, d will represent the distance between the plates.
The charge on the capacitor plates is equal in magnitude, so we can consider the field strength created by only one of the plates.
The field strength of one plate is equal to E/2 , where E is the field strength in the capacitor.
In a uniform field of one plate there is a charge q distributed over the surface of the other plate.
Then the energy of the capacitor is:
Wp = qEd/2
The potential difference between the plates of a capacitor can be represented as the product of voltage and distance:
U = Ed
That's why:
Wp = qU/2
This energy is equal to the work done by the electric field when the plates are brought closer together.
Replacing the potential difference or charge in the formula using the expression for the electrical capacity of the capacitor C = q/U , we obtain three different formulas for the energy of the capacitor:
| Capacitor energy Wp = qU/2 Wp – electrostatic field energy [J] q —electric charge [C] U – voltage across the capacitor [V] |
| Capacitor energy Wp = q2/2C Wp – electrostatic field energy [J] q —electric charge [C] C —capacitance of the capacitor [F] |
| Capacitor energy Wp = CU2/2 Wp – electrostatic field energy [J] C —capacitance of the capacitor [F] U – voltage across the capacitor [V] |
These formulas are valid for any capacitor.
Flat capacitor
A parallel plate capacitor is two oppositely charged plates that are separated by a thin layer of dielectric, as shown in Figure 1.
The formula for calculating electrical capacity is written as
C = ε ε 0 S d , where S is the area of the plate, d is the distance between them, ε is the dielectric constant of the substance. A smaller value of d makes the calculated capacitance of the capacitor more closely match the actual one.
With a known electrical capacity of a capacitor filled with N layers of dielectric, the thickness of the layer with number i is equal to di, the dielectric constant of this layer ε i is calculated based on the formula:
Expert opinion
It-Technology, Electrical power and electronics specialist
Ask questions to the “Specialist for modernization of energy generation systems”
Slobodyanyuk A.I. Physics 10/16.1 - PhysBook The force of interaction between two point-fixed charged bodies in a vacuum is directly proportional to the product of the charge modules and inversely proportional to the square of the distance between them. Ask, I'm in touch!
Application of capacitors
There is a capacitor in every modern device. Let's look at two of the most obvious examples.
Example time - flash
Without a capacitor, the flash in the camera would not work as we are used to, but with long delays, and would also quickly drain the battery. The capacitor in this case works like a battery. It accumulates charge from the battery and stores it until needed. When we need a flash, the capacitor discharges so that it fires and the bird flies out.
formulas for capacitors
One of the important elements of the electrical circuit is a capacitor, the formulas for which allow you to calculate and select the most suitable option. The main function of this device is to accumulate a certain amount of electricity. The simplest system includes two electrodes or plates separated by a dielectric.
- What is the capacitance of a capacitor measured in?
- Capacitor Energy Formula
- Capacitor charge formula
- Capacitor Leakage Current Formula
What is the capacitance of a capacitor measured in?
One of the most important characteristics of a capacitor is its capacity. This parameter is determined by the amount of electricity accumulated by this device. The accumulation occurs in the form of electrons. The number of them placed in the capacitor determines the capacitance value of a particular device.
The unit used to measure capacitance is the farad. A capacitor's capacity of 1 farad corresponds to an electric charge of 1 coulomb, and the potential difference across the plates is 1 volt. This classical formulation is not suitable for practical calculations, since the capacitor collects not charges, but electrons. The capacity of any capacitor is directly dependent on the volume of electrons that can accumulate during normal operating conditions. The farad is still used to denote capacitance, and the quantitative parameters are determined by the formula: C = Q / U, where C means capacitance, Q is charge in coulombs, and U is voltage. Thus, the mutual relationship between charge and voltage is visible, influencing the capacitor’s ability to accumulate and retain a certain amount of electricity.
To calculate the capacitance of a parallel-plate capacitor, the formula is used: in which ε = 8.854187817 x 10 -12 f/m is a constant value. Other quantities: ε is the dielectric constant of the dielectric located between the plates, S is the area of the plate, and d is the gap between the plates.
Measuring capacitance of a capacitor with a multimeter and special devices
Some multimeters have a capacitance measurement feature. Take these common models: M890D, AM-1083, DT9205A, UT139C, etc.
Using any of these devices, you can not only find out the exact capacitance of the capacitor, but also make sure that there is no short circuit between the plates or an internal break in one of the terminals.
Read also: Hephaestus oven temperature by numbers
Some manufacturers even claim that their multimeters can test the capacitance of a capacitor without desoldering it from the board. Which, of course, contradicts common sense.
Unfortunately, testing a capacitor with a multimeter will not help determine the most important parameters such as leakage current and equivalent series resistance (ESR). They can only be measured using specialized testers. For example, using a very inexpensive LC meter.
Capacitor charge formula
To perform charging, the capacitor must be connected to a DC circuit. A generator can be used for this purpose. Every generator has internal resistance. When the circuit is closed, the capacitor is charged. A voltage appears between its plates equal to the electromotive force of the generator: Uc = E.
The plate connected to the positive pole of the generator is charged positively (+q), and the other plate receives an equal charge with a negative value (-q). The amount of charge q is directly proportional to the capacitance of the capacitor C and the voltage on the plates Uc. This dependence is expressed by the formula: q = C x Uc.
During the charging process, one of the capacitor plates gains and the other loses a certain number of electrons. They are transferred through an external circuit under the influence of the electromotive force of the generator. This movement is an electric current, also known as charging capacitive current (Icharge).
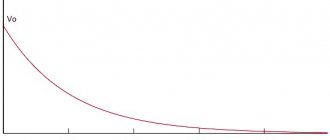
The charging current flows in the circuit in almost thousandths of a second, until the moment the capacitor voltage becomes equal to the electromotive force of the generator. The voltage increases smoothly and then gradually slows down. Further, the capacitor voltage value will be constant. During charging, a charging current flows through the circuit. At the very beginning, it reaches its maximum value, since the capacitor voltage has a zero value. According to Ohm's law, Izar = E/Ri, since the entire emf of the generator is applied to the resistance Ri.
Supercapacitor idea
Electricity is an extremely versatile form of energy , but has one drawback - it is difficult to accumulate quickly. Chemical batteries can store large amounts of energy but require several hours to fully charge. Capacitors do not have this disadvantage - they can be charged almost instantly. But their capacity does not allow storing large amounts of energy, so the idea of a supercapacitor, combining the best qualities of chemical and electrostatic electricity storage devices, looks very tempting.
Despite the functional similarity, batteries and capacitors are designed completely differently. Galvanic cells work on the principle of releasing electrical energy during a chemical reaction of substances within them. When the supply of active reagents is depleted, they stop generating a potential difference and for a new cycle they require the initiation of reverse chemical reactions by current to restore the active substances. The main disadvantages of batteries compared to capacitors:
- short life cycle;
- low power density;
- narrow range of charging and discharging temperatures;
- inability to quickly give up all energy reserves.
However, conventional capacitors are not used as active voltage sources due to their low capacitance. Theoretical and practical supercapacitors (ultracapacitors) differ from conventional ones in their extremely high capacity with a high stored energy density, which allows them to be considered as an alternative to chemical elements.
The largest commercial devices have capacities of up to several thousand farads, but their capabilities are still not comparable to batteries, so such devices are used to store charges for a relatively short period of time. They have found widespread use as the electrical equivalent of mechanical flywheels to smooth out the voltage of power supplies, for example in wind turbines or regenerative braking systems in electric vehicles.
The first ultracapacitors appeared in the middle of the last century and had not very impressive capacities. Since then, progress in improving materials has led to the thinning of the dielectric layer to a single molecule, which has made it possible to create devices with outstanding characteristics. The further development of the nanoindustry became the basis for fundamental changes in electricity storage. Perhaps, in the near future, environmentally hazardous and capricious chemical batteries will be replaced by supercapacitors based on molecularly structured plates and a dielectric layer.