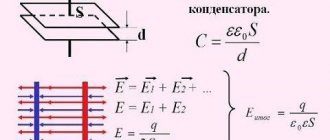
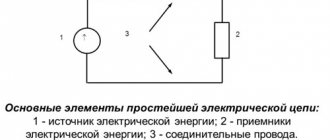
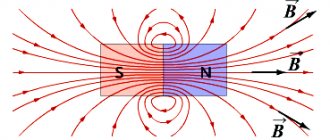
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи
, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против
движения заряда (т.е. против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).
Рис. 1. Сторонняя сила
Эта сила называется сторонней силой
; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят,
неэлектрическое
происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока
.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи
.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой
(ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Баланс энергии электромагнитного поля. Вектор Умова-Пойтинга
Лекция № 8.
Энергия электромагнитного поля
Учебные вопросы лекции:
Сторонние источники электромагнитного поля. Закон Джоуля–Ленца.
Баланс энергии электромагнитного поля. Вектор Умова-Пойнтинга.
Вектор Умова-Пойнтинга для гармонических полей.
Введение
В данной лекции рассматривается закон сохранения энергии применительно к электромагнитному полю. Физическая реальность электромагнитного поля в первую очередь проявляется в переносе энергии полем в пространстве. Непосредственное воздействие быстропеременного ЭМП на органы чувств человека вызывает ощущение тепла, а при определенной частоте колебаний – света. Однако основной научный и практический интерес представляет превращение энергии поля в иные формы, доступные наблюдению и изучению, ее виды и характер распределения в пространстве. С этой целью будет рассмотрен баланс энергии в ограниченной области пространства. В результате анализа появятся понятия потока энергии и вектора Умова-Пойнтинга, электрической и магнитной энергии.
Сторонние источники электромагнитного поля. Закон Джоуля–Ленца
В первом вопросе вводится понятие сторонних источников поля и их учет в уравнениях Максвелла, формулируются закон Джоуля-Ленца.
При рассмотрении электромагнитных процессов часто приходится иметь дело с вопросом возбуждения или создания поля (например, в теории антенн). Источник возникновения электромагнитного поля принято называть сторонней силой (или сторонним источником
). Как правило,
в качестве источника возбуждения электромагнитного поля выбираются токи и заряды, создаваемые каким-либо генератором, не входящим в область, где рассматривается электромагнитное поле. Между сторонними токами (зарядами) и создаваемыми ими полями имеется очевидное соответствие по частоте колебаний и в функциональной зависимости от времени.
Учет сторонних токов и зарядов производят путем введения их в качестве дополнительных слагаемых в выражения для плотности тока проводимости и объемной плотности заряда:
; , (1)
где: – плотность стороннего тока проводимости; rст – объемная плотность стороннего электрического заряда.
Знак «–» означает, что ток или заряд привносится из вне. С учетом (1) система уравнений Максвелла в дифференциальной форме примет вид:
(2)
Отметим, что в большинстве случаев значения и rст предполагаются заданными.
Определим работу, производимую электромагнитным полем при перемещении объемного заряда r в элементарном объеме ΔV на расстояние , где: – скорость перемещения заряда:
. (3)
Здесь – сила Лоренца, как показано в лекции №4. Параметром Q обозначена величина заряда внутри рассматриваемого элементарного объема ΔV. Из выражения (3) следует, что, во-первых, неподвижные заряды не могут производить работу, т.к. и, во-вторых, не совершает работу магнитная компонента поля, поскольку направление силы и направление скорости перемещения заряда взаимно перпендикулярны, поэтому всегда .
Из курса общей физики известно, что мощность связана с работой отношением: р = А/t. Следовательно, мощность, выделяемую в единице объема ΔV (которая называется также удельной мощностью), можно определить как:
. (4)
Учитывая, что вектор плотности тока проводимости , определим теперь полную мощность, выделяемую в объеме V:
. (5)
Полученное выражение (5) является известным законом Джоуля-Ленца в интегральной форме, а выражение (4) соответственно законом Джоуля-Ленца в дифференциальной форме.
Закон Джоуля-Ленца – физический закон, дающий количественную оценку теплового действия электрического тока. Открыт в 1841 году независимо английским физиком Джеймсом Джоулем и российским физиком немецкого происхождения Эмилем Ленцом.
В словесной формулировке звучит следующим образом – мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля.
Если плотность тока обусловлена только плотностью током проводимости (как в данном случае), то мощность, определяемая по (5), является мощностью тепловых потерь, выделяемых за счет протекания тока проводимости. Другими словами, речь идет о преобразовании электромагнитной энергии в другие виды энергии.
Если же в рассматриваемой области V действуют сторонние силы, то тогда уравнение (5) с учетом выражения (1) примет вид:
. (6)
Рст – называется мощностью сторонних сил, выделяемой в объеме V, эта мощность характеризует процесс преобразования энергии различных видов (например механической, химической и др.) в электромагнитную энергию;
Рпот – мощность тепловых потерь, выделяемых за счет протекания тока проводимости.
Баланс энергии электромагнитного поля. Вектор Умова-Пойтинга
В этом вопросе формулируется закон сохранения энергии применительно к электромагнитному полю, дается физический смысл вектора Умова-Пойнтинга.
Выделим некоторый объем V, ограниченный поверхностью S, в котором находятся некие источники ЭМП. Поскольку закон сохранения энергии является фундаментальным законом физики, то очевидно утверждать, что энергия источников поля затрачивается на выделение тепла (или на переход в другие виды энергии), на накопление энергии ЭМП внутри объема V и на переход (излучение) энергии из этого объема в прилегающее к нему пространство, то есть:
Рст = Рпот + Рзап + Рпер (7)
где: Рст – мощность, выделяемая сторонними источниками; Рпот – мощность тепловых потерь; Рзап – мощность, затрачиваемая на накопление энергии ЭМП (запасаемая мощность); Рпер – мощность, выходящая из рассматриваемого объема.
Определим конкретные значения составляющих выражения (7). Возьмем 1-ое и 2-ое уравнения Максвелла в дифференциальной форме с учетом сторонних сил и помножим 1-ое уравнение на , а 2-ое уравнение на вектор :
(8 а)
(8 б)
Далее вычтем из (8 б) выражение (8 а) в результате получим:
.
Преобразуем левую часть полученного выражения, используя известное тождество из векторного анализа,
,
где — произвольные векторы; — обозначает векторное произведение.
В результате получим, что дивергенция скалярного произведения векторов напряженности электрического и магнитного поля равна:
. (9)
Проинтегрируем данное выражение по объему V, ограниченному замкнутой поверхностью:
.
Применив к левой части полученного уравнения теорему Остроградского – Гаусса, получим:
.
Перегруппируем данное выражение, оставив в правой части лишь составляющую, содержащую плотность тока сторонних сил, тогда окончательно:
. (10)
Полученное уравнение (10) называют теоремой Умова-Пойтинга в интегральной форме. Оно характеризует баланс энергии электромагнитного поля в замкнутом объеме V, ограниченном поверхностью S.
Выясним физический смысл отдельных членов, входящих в выражение (10).
1) Физический смысл интеграла ясен из выражения (6). Он характеризует мощность сторонних сил, которая выделяется в рассматриваемом объеме V.
2) Выражение характеризует мощность тепловых потерь в рассматриваемом объеме V, создаваемых за счет протекания тока проводимости.
3) Для выяснения физического смысла выражения рассмотрим особый случай:
– пусть сторонние источники в объеме V отсутствуют, тогда Рст = 0;
– кроме того, пусть граница S непроницаема для электромагнитного поля (т.е. является идеально проводящей), тогда, поскольку поле на границе S отсутствует ( и ), то .
В этом случае, получаем:
.
Отсюда делаем первый вывод: рассматриваемый интеграл характеризует некую мощность в объеме V. Далее, поскольку область V не сообщается с внешней средой (S — непроницаема), то отсюда следует, что рассматриваемый интеграл будет характеризовать мощность, запасенную в объеме V. Так как в нашем случае эта мощность расходуется на потери (нагрев среды) то, очевидно, запасенная мощность Рзап должна убывать. Этому как раз и соответствует знак «–».
Из курса общей физики известно, что мощность связана с энергией как , тогда:
.
Вывод: Рассматриваемый интеграл характеризует скорость изменения электромагнитной энергии, сосредоточенной внутри области V, другими словами мощность, запасенную в этой области. Интеграл характеризует мощность электрического поля, сосредоточенную в объеме V, а интеграл характеризует соответственно мощность магнитного поля, сосредоточенную в этом же объеме.
4) Для выяснения физического смысла интеграла также рассмотрим особый случай:
– пусть отсутствуют потери на нагрев среды, т.е. Рпот = 0;
– электромагнитная энергия внутри области V остается постоянной, следовательно, dW/dt = 0.
В этом случае получаем:
.
Отсюда можно сделать первый вывод: рассматриваемый интеграл есть мощность, кроме того, поскольку данный интеграл берется по замкнутой поверхности S, то это мощность, проходящая через поверхность S. Так как потери отсутствуют, а запасенная энергия постоянна в данном объеме (Wзап = const), то мощность сторонних сил расходуется на излучение электромагнитной энергии из рассматриваемого объема V. Следовательно, в данном случае интеграл характеризует мощность излучения Ризл.
В случае, когда Рст = 0 , W = const, получаем: , и в данном случае рассматриваемый интеграл характеризует мощность, которая входит через поверхность S (обратите внимание на знак «–») в объем V и расходуется там в виде потерь.
Вывод: Рассматриваемый интеграл характеризует мощность, которая в зависимости от знака, либо выходит («+»), либо входит («–») через поверхность S, рассматриваемого объема V. Таким образом, этот интеграл характеризует мощность перехода между выделенным объемом и внешним, по отношению к этому объему, пространством.
Векторное произведение составляющих электромагнитного поля называют вектором Умова-Пойнтинга .
Определим единицу измерения вектора Умова-Пойнтинга. Поскольку измеряется в В/м, а — в А/м, то очевидно, что для единицей измерения является В×А/м2 = Вт/м2 . Таким образом, вектор Умова-Пойнтинга характеризует мгновенное значение плотности мощности, проходящей через замкнутую произвольную поверхность S в один квадратный метр, параллельную плоскости, в которой расположены векторы и .
Исходя и вышеизложенного, запишем уравнение баланса электромагнитного поля, которое также носит название закона сохранения электромагнитной энергии:
. (11)
В заключение этого вопроса рассмотрим два частных примера, изображенных на рис. 1.
а) б)
Рис. 1 – Примеры для выяснения смысла уравнения баланса ЭМП
Запишем уравнение баланса электромагнитного поля для этих примеров. Для случая на рис. 1 а, когда рассматривается объем, в котором присутствуют сторонние силы (эту роль выполняет передающая антенна), уравнение баланса принимает вид:
Рст = Рпот + Рзап + Ризл = .
Для случая на рис. 1 б, когда рассматривается объем, в котором отсутствуют сторонние силы, очевидно, что уравнение баланса будет иметь вид:
Рпот + Рзап = – Рприем = .
Мощность излучения Ризл или мощность приема Рприем являются мощностью перехода, т.е. мощностью, проходящую через замкнутую поверхность S рассматриваемого объема V.
Вывод:Конкретный вид уравнения баланса определяется рассматриваемой областью V при заданных источниках сторонних сил.
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением
этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором
, или
внешней нагрузкой
, или
полезной нагрузкой
). Всё это вместе называется
полной цепью
(рис. 2).
Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи
.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание
. Через источник при этом потечёт максимальный ток —
ток короткого замыкания
:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника
.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока
. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь
. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС
.
От электростатики к электрокинетике
Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.
Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.
Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.
Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.
Вам это будет интересно Описание и разновидности вводно-распределительных устройств (ВРУ)
Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:
- 1800 г. — создание Вольтой гальванической батареи;
- 1826 г. — Ом формулирует свой закон для полной цепи;
- 1831 г. — обнаружение электромагнитной индукции Фарадеем.
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной
, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи
— это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Как измеряется внутреннее сопротивление
Для определения значения рассматриваемой характеристики применяются измерения во время прямого замыкания клемм, которое называют коротким замыканием. Как известно, если закоротить клеммы источника, между ними протечёт значительный ток. Часто это является следствием неосторожности и приводит к обгоранию изоляции и расплавлению провода.
При коротком замыкании сопротивление цепи становится минимальным. Точно измерив силу тока в этой ситуации и зная величину напряжения на клеммах при отсутствии нагрузки, можно определить внутреннее сопротивление источника питания. Для этого понадобится следующая формула:
r = U / I(зам), где
- буквой r обозначено внутреннее сопротивление источника тока;
- U — разность потенциалов на клеммах батареи без подсоединения к электрической цепи;
- I(зам) — ток, который проходит при непосредственном замыкании клемм друг на друга.
Находить значение нагрузки таким образом не всегда возможно или целесообразно, поскольку короткое замыкание может стать причиной серьезной аварии.
Поэтому используются другие решения вопроса, как найти внутреннее сопротивление источника. Например, с помощью специальных измерительных приборов. Функцией измерения данного параметра снабжены оригинальные зарядные устройства iMax B6, ToolkinRC M8, M6, M600.