Kirchhoff's method, first and second laws...

In complex electrical circuits, that is, where there are several different branches and several sources of EMF, a complex distribution of currents also occurs. However, with known values of all EMF and resistance of resistive elements in the circuit, we can clear the values of these currents and their direction in any circuit circuit using Kirchhoff's first and second laws. The rules were formulated in 1845; this is not Kirchhoff’s only discovery. Kirchhoff and Bunsen actively studied the emission spectra of chemical elements using Fraunhofer's inventions. Using a prism or diffraction grating, the light was decomposed into spectral components, and scientists observed the effect. This is how the individual frequencies of a number of elements in the periodic table were established. These scientists laid the foundations of spectroscopy. Kirchhoff devoted a lot of time to various branches of science. For example, he found an error in setting the boundary conditions for solving differential equations for membrane vibrations, presented to the public in 1811 by Sophie Germain. One should not think that the phrase Kirchhoff’s law is narrowly limited to two rules, one of which directly leads to Ohm’s law formulated earlier.

German Gustav Robert Kirchhoff

Date of Birth	March 12, 1824

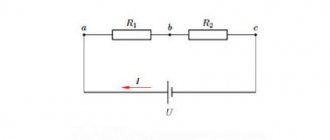
An example of a complex electrical circuit can be seen in Figure 1.

Figure 1. Complex electrical circuit.

Sometimes Kirchhoff's laws are called Kirchhoff's rules , especially in older literature.

So, to begin with, let me remind you of the essence of Kirchhoff’s first and second laws, and then consider examples of calculating currents and voltages in electrical circuits, with practical examples and answers to questions that were asked to me in the comments on the site.

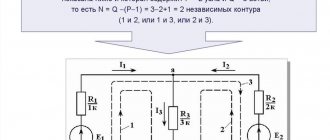
The most accurate method, but with its help you can determine the parameters of a circuit with a small number of circuits (1-3). Algorithm: 1. Determine the number of nodes q, branches p and independent circuits; 2. Set the directions of currents and circuit bypasses arbitrarily; 3. Establish the number of independent equations according to Kirchhoff’s 1st law (q - 1) and compose them, where q is the number of nodes; 4. Determine the number of equations according to Kirchhoff’s 2nd law (p – q + 1) and compose them; 5. Solving the equations together, we determine the missing parameters of the circuit; 6. Based on the data received, the calculations are checked by substituting the values into the equations according to Kirchhoff’s 1st and 2nd laws or by compiling and calculating the power balance. Example:

Fig. 1. According to the proposed algorithm, we determine the number of nodes and branches of the circuit in Fig. 1 q = 3, p = 5, therefore, there are 2 equations according to Kirchhoff’s 1st law, and there are 3 equations according to Kirchhoff’s 2nd law. Let’s write these equations according to the rules:

Let's create the power balance equations:

Kirchhoff's rules and laws

Kirchhoff's rules (often called Kirchhoff's Laws in technical literature) are relationships that hold between currents and voltages in sections of any electrical circuit.

Solutions of systems of linear equations compiled on the basis of Kirchhoff's rules make it possible to find all currents and voltages in electrical circuits of direct, alternating and quasi-stationary current.

They are of particular importance in electrical engineering because of their versatility, as they are suitable for solving many problems in the theory of electrical circuits and practical calculations of complex electrical circuits.

Application of Kirchhoff's rules to a linear electrical circuit allows us to obtain a system of linear equations for currents or voltages and, accordingly, when solving this system, find the current values on all branches of the circuit and all internodal voltages.

Formulated by Gustav Kirchhoff in 1845.

The name “Rules” is more correct because these rules are not fundamental laws of nature, but follow from the fundamental laws of conservation of charge and irrotation of the electrostatic field (Maxwell’s third equation with a constant magnetic field). These rules should not be confused with two more Kirchhoff laws in chemistry and physics.

Current strength and Ohm's law

When calculating the current strength of a circuit, it should be remembered that this quantity is of a physical type, demonstrating a certain charge. It flows for a certain time unit along the conductor. The basic calculation scheme is as follows:

I=q/t , where:

I is the power of electricity in Amperes (A) or C/s;
q – charge moving within the conductor in Coulombs (C);
t – time spent moving the charge, s.

In accordance with the provisions of Ohm's law, for a separate part of the circuit, when calculating the current strength, a diagram is used showing:

direct dependence of current on voltage;
inverse relationship with resistance.

I=U/R , where:

U – voltage expressed in volts, V;
R – resistance indicator, Ohm.

From here the following dependence will follow:

I = E/ R+r , where:

E – emf, V;
R – external type resistance, Ohm
r – internal resistance, Ohm

Use other online calculators:

Kirchhoff's first law

Formulation No. 1: The sum of all currents flowing into a node is equal to the sum of all currents flowing out of the node.

Formulation No. 2: The algebraic sum of all currents in a node is equal to zero.

[[s|kirgof1.txt]]

Let us explain Kirchhoff's first law using the example of Figure 2.

Figure 2. Electrical circuit assembly.

Here the current I1 is the current flowing into the node, and the currents I2 and I3 are the currents flowing out of the node. Then, using formulation No. 1, we can write:

I1 = I2 + I3 (1)

To confirm the validity of formulation No. 2, we transfer the currents I2 and I 3 to the left side of expression (1) , thereby obtaining:

I1 - I2 - I3 = 0 (2)

The minus signs in expression (2) mean that currents flow out of the node.

The signs for inflowing and outflowing currents can be taken arbitrarily, however, in general, inflowing currents are always taken with a “+” sign, and outflowing currents with a “-” sign (for example, as happened in the expression (2)).

Calculation of electrical circuits online

A program has appeared on the website for calculating steady-state conditions of electrical circuits according to the laws of TOE. At the moment, calculation methods have been implemented using Ohm's laws, Kirchhoff's laws, the nodal potential method, the loop current method, and the equivalent generator method. The program also allows you to calculate the equivalent resistance of the circuit relative to the power source. The program allows you to draw a diagram, set the parameters of its elements and calculate the diagram. As a result, a text description of the calculation procedure is generated, the power balance is calculated and vector diagrams are constructed.

Drawing a diagram is done by drag-and-dropping elements from the sidebar and then connecting the selected elements.

The following elements with configurable parameters are available in the sidebar:

resistor: element number;
resistance, Ohm;

capacitor:

item number;

resistance, Ohm;

inductor :

item number;

resistance, Ohm;

EMF source:

item number;

amplitude value, V;

initial phase, °;

current source:

item number;

amplitude value, V;

initial phase, °.

Instructions for using the program are given here.

Calculation methods

After completing drawing the diagram, clicking the “Calculation” button starts the calculation of the electrical circuit. The program analyzes the source circuit and if any errors are detected, it reports this. Upon successful analysis of the circuit, the calculation using TOE methods is started.

Calculation according to Ohm's law

Calculation according to Ohm's law is carried out for single-circuit circuits. The calculation method used is given here.

Example diagram and calculation:

Initial data and diagram:

E1: Item number: 1
Amplitude value: 100 V
Initial phase: 0

R1:

Item number: 1

Resistance, Ohm: 1

After clicking the “Calculation” button, a solution is generated:

The original circuit has only one circuit. Let's calculate it using Ohm's law.

According to Ohm's law, the current in a closed circuit is equal to the ratio of the circuit's emf to the resistance. Let's create an equation, taking the positive direction of the current $ \underline{I} $ to be the direction of the EMF source $ \underline{E}_{1} $:

$$ R_{1}\cdot \underline{I} = \underline{E}_{1} $$

Let us substitute the values of resistances and sources into the resulting system of equations and obtain:

$$ 1.0\cdot \underline{I}=100 $$

Hence the required current in the circuit is equal to

$$ \underline{I} = 100\space \textrm{A}$$

Calculation according to Kirchhoff's laws

For multi-circuit circuits, the calculation is carried out according to Kirchhoff's laws. The calculation method used is given here.

Example diagram and calculation:

Initial data and diagram:

E1: Item number: 1
Amplitude value: 100 V
Initial phase: 0

R1:

Item number: 1

Resistance, Ohm: 1

L1:

Item number: 1

Resistance, Ohm: 1

C1:

Item number: 1

Resistance, Ohm: 1

After clicking the “Calculation” button, the numbering of nodes appears on the original diagram and a solution is generated:

Let's calculate the circuit using Kirchhoff's laws.

In this scheme: nodes - 2, branches - 3, independent circuits - 2.

Let us arbitrarily set the directions of currents in the branches and the directions of traversal of the circuits.

Accepted directions of currents: Current $ \underline{I}_{1} $ is directed from node '2 y.' to node '1 y.' through the elements $ \underline{E}_{1} $, $ R_{1} $. Current $ \underline{I}_{2} $ is directed from node '1 y.' to node '2 y.' through the elements of $L_{1}$. Current $ \underline{I}_{3} $ is directed from node '1 y.' to node '2 y.' through the elements of $C_{1}$.

Accepted directions for traversing contours: Contour No. 1 is traversed through the elements $ \underline{E}_{1} $, $ R_{1} $, $ L_{1} $ in the specified order. Circuit No. 2 is traversed through the elements $ L_{1} $, $ C_{1} $ in the specified order.

Let's create equations according to Kirchhoff's first law. When drawing up equations, we will take currents “flowing” into a node with a “+” sign, and “outgoing” ones with a “−” sign.

The number of equations compiled according to Kirchhoff's first law is equal to $ N_\textrm{y} − 1 $, where $ N_\textrm{y} $ is the number of nodes. For this scheme, the number of equations according to Kirchhoff’s first law is 2 − 1 = 1.

Let's create an equation for node No. 1:

$$ \underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3} = 0 $$

Let's create equations using Kirchhoff's second law. When drawing up equations, positive values for currents and EMF are selected if they coincide with the direction of traversal of the circuit.

The number of equations compiled according to Kirchhoff's second law is equal to $ N_\textrm{в} − N_\textrm{у} + 1 $, where $ N_\textrm{в} $ is the number of branches. For this scheme, the number of equations according to Kirchhoff’s second law is 3 − 2 + 1 = 2.

Let's create an equation for circuit No. 1:

$$ R_{1}\cdot \underline{I}_{1} + jX_{L1}\cdot \underline{I}_{2}=\underline{E}_{1} $$

Let's create an equation for circuit No. 2:

$$ jX_{L1}\cdot \underline{I}_{2} − (−jX_{C1})\cdot \underline{I}_{3}=0 $$

Let us combine the resulting equations into one system, and at the same time transfer the known quantities to the right side, leaving only the components with the required currents on the left side. The system of equations according to Kirchhoff’s laws for the original circuit is as follows:

$$ \begin{cases}\underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3} = 0 \\ R_{1}\cdot \underline{I }_{1}+jX_{L1}\cdot \underline{I}_{2} = \underline{E}_{1} \\ jX_{L1}\cdot \underline{I}_{2}−( −jX_{C1})\cdot \underline{I}_{3} = 0 \\ \end{cases} $$

Let us substitute the values of resistances and sources into the resulting system of equations and obtain:

$$ \begin{cases}\underline{I}_{1} − \underline{I}_{2} − \underline{I}_{3}=0 \\ \underline{I}_{1}+ j \cdot \underline{I}_{2}=100 \\ j \cdot \underline{I}_{2}+ j \cdot \underline{I}_{3}=0 \\ \end{cases} $$

Let us solve the system of equations and obtain the required currents:

$$ \underline{I}_{1} = 0 $$

$$ \underline{I}_{2} = −100j $$

$$ \underline{I}_{3} = 100j $$

Kirchhoff's second law.

Formulation: The algebraic sum of the EMF acting in a closed circuit is equal to the algebraic sum of the voltage drops across all resistive elements in this circuit.

[[s|kirgof2.txt]]

Here the term “algebraic sum” means that both the magnitude of the EMF and the magnitude of the voltage drop across the elements can be either with a “+” or a “-” sign. In this case, the sign can be determined using the following algorithm:

1. Select the direction of traversing the contour (two options, either clockwise or counterclockwise).

2. We arbitrarily select the direction of currents through the circuit elements.

3. We arrange signs for the EMF and voltages falling on the elements according to the rules:

— EMF that creates a current in the circuit, the direction of which coincides with the direction of bypassing the circuit, is written with a “+” sign, otherwise the EMF is written with a “-” sign.

— voltages falling across the circuit elements are recorded with a “+” sign if the current flowing through these elements coincides in the direction of bypassing the circuit, otherwise the voltages are recorded with a “-” sign.

For example, consider the circuit shown in Figure 3 and write the expression according to Kirchhoff's second law, going around the circuit clockwise and choosing the direction of the currents through the resistors, as shown in the figure.

Figure 3. Electric circuit to explain Kirchhoff's second law.

E1- E2 = -UR1 - UR2 or E1 = E2 - UR1 - UR2 (3)

Calculation of DC electrical circuits using the method of equivalent transformations

Home → Examples of solving TOE problems → Calculation of DC electrical circuits by the method of equivalent transformations Calculation of DC electrical circuits by the method of equivalent transformations

The basic laws that determine the calculation of an electrical circuit are Kirchhoff's laws.

Based on Kirchhoff's laws, a number of practical methods for calculating DC electrical circuits have been developed, allowing to reduce calculations when calculating complex circuits.

It is possible to significantly simplify calculations, and in some cases reduce the complexity of calculations, using equivalent circuit transformations.

Converts parallel and series connections of elements, a star connection into an equivalent delta connection and vice versa. The current source is replaced with an equivalent EMF source. Using the method of equivalent transformations, it is theoretically possible to calculate any circuit, and at the same time use simple computing tools. Or determine the current in any one branch, without calculating the currents of other sections of the circuit.

This article on the theoretical foundations of electrical engineering examines examples of the calculation of linear DC electrical circuits using the method of equivalent transformations of typical circuits for connecting energy sources and consumers, and provides calculation formulas.

Problem solving Calculation of DC electrical circuits by the method of equivalent transformations

Task 1. For the circuit (Fig. 1), determine the equivalent resistance relative to the input terminals a−g, if known: R1 = R2 = 0.5 Ohm, R3 = 8 Ohm, R4 = R5 = 1 Ohm, R6 = 12 Ohm, R7 = 15 Ohm, R8 = 2 Ohm, R9 = 10 Ohm, R10 = 20 Ohm.

Rice. 1

Solution

Let's start the equivalent transformations of the circuit from the branch furthest from the source, i.e. from terminals a−g:

Task 2. For the circuit (Fig. 2, a), determine the input resistance if it is known: R1 = R2 = R3 = R4 = 40 Ohm.

Rice. 2

Solution

The original circuit can be redrawn relative to the input terminals (Fig. 2, b), from which it can be seen that all resistances are connected in parallel. Since the resistance values are equal, to determine the equivalent resistance value, you can use the formula:

where R is the resistance value, Ohm;

n – number of parallel connected resistances.

Task 3. Determine the equivalent resistance relative to terminals a–b, if R1 = R2 = R3 = R4 = R5 = R6 = 10 Ohm (Fig. 3, a).

Rice. 3

Solution

Let us transform the delta connection f−d−c into the equivalent star connection. We determine the values of the converted resistances (Fig. 3, b):

According to the conditions of the problem, the values of all resistances are equal, which means:

In the transformed circuit, we obtained a parallel connection of branches between nodes e–b, then the equivalent resistance is equal to:

And then the equivalent resistance of the original circuit is a series connection of resistances:

Task 4. In a given circuit (Fig. 4, a) determine the input resistances of branches a−b, c–d and f−b using the method of equivalent transformations, if it is known that: R1 = 4 Ohm, R2 = 8 Ohm, R3 =4 Ohm, R4 = 8 Ohm, R5 = 2 Ohm, R6 = 8 Ohm, R7 = 6 Ohm, R8 =8 Ohm.

Solution

To determine the input resistance of the branches, all sources of EMF are excluded from the circuit. In this case, points c and d, as well as b and f, are short-circuited, because The internal resistance of ideal voltage sources is zero.

Rice. 4

Branch a−b is broken, and since resistance Ra–b = 0, then the input resistance of the branch is equal to the equivalent resistance of the circuit relative to points a and b (Fig. 4, b):

Similarly, the input resistances of the branches Rcd and Rbf are determined by the method of equivalent transformations. Moreover, when calculating resistances, it is taken into account that short-circuiting points a and b excludes (“short-circuits”) resistances R1, R2, R3, R4 from the circuit in the first case, and R5, R6, R7, R8 in the second case.

Task 5. In the circuit (Fig. 5) currents I1, I2, I3 using equivalent transformations draw up a power balance , if known: R1 = 12 Ohm, R2 = 20 Ohm, R3 = 30 Ohm, U = 120 V.

Rice. 5

Solution

Equivalent resistance for parallel connected resistances:

Equivalent resistance of the entire circuit:

Current in the unbranched part of the circuit:

Voltage across parallel resistances:

Currents in parallel branches:

Power balance:

Task 6. In the circuit (Fig. 6, a), determine the ammeter readings using the method of equivalent transformations , if it is known: R1 = 2 Ohm, R2 = 20 Ohm, R3 = 30 Ohm, R4 = 40 Ohm, R5 = 10 Ohm, R6 = 20 Ohm, E = 48 V. The resistance of the ammeter can be considered zero.

Rice. 6

Solution

If resistances R2, R3, R4, R5 are replaced by one equivalent resistance RE, then the original circuit can be represented in a simplified form (Fig. 6, b).

Equivalent resistance value:

By transforming the parallel connection of resistances RE and R6 of the circuit (Fig. 6, b), we obtain a closed circuit for which, according to Kirchhoff’s second law, we can write the equation:

where does the current I1 come from:

We express the voltage at the terminals of parallel branches Uab from the equation according to Ohm’s law for the passive branch obtained by transforming RE and R6:

Then the ammeter will show the current:

Task 7. Determine the currents of the circuit branches by the method of equivalent transformations (Fig. 7, a), if R1 = R2 = R3 = R4 = 3 Ohm, J = 5 A, R5 = 5 Ohm.

Rice. 7

Solution

Let us transform the “triangle” of resistances R1, R2, R3 into an equivalent “star” R6, R7, R8 (Fig. 7, b) and determine the values of the resulting resistances:

Let's transform the parallel connection of branches between nodes 4 and 5

The current in the circuit obtained as a result of the transformations is considered equal to the current of the current source J, and then the voltage:

And now you can determine the currents I4 and I5:

Returning to the original circuit, we determine the voltage U32 from the equation according to Kirchhoff’s second law:

Then the current in the branch with resistance R3 will be determined:

The values of the remaining unknown currents can be determined from the equations according to Kirchhoff’s first law for nodes 3 and 1:

Electronic version of the article Calculation of DC electrical circuits by the method of equivalent transformations

Examples of problem solving Calculation of DC electrical circuits by the method of equivalent transformations

Calculation of DC electrical circuits using the method of equivalent transformations

Equivalent transformation method

09/02/2011, 305294 views.
Add a comment

Kirchhoff's radiation law

Kirchhoff's radiation law states that the ratio of the emissivity of any body to its absorption capacity is the same for all bodies at a given temperature for a given frequency for equilibrium radiation and does not depend on their shape, chemical composition, etc.

In its modern formulation, the law reads as follows:

The ratio of the emissivity of any body to its absorption capacity is the same for all bodies at a given temperature for a given frequency and does not depend on their shape and chemical nature.

It is known that when electromagnetic radiation falls on a certain body, part of it is reflected, part is absorbed, and part can be transmitted. The fraction of radiation absorbed at a given frequency is called the body's absorptivity. On the other hand, every heated body emits energy according to a certain law called the emissivity of the body.

The values of and can vary greatly when moving from one body to another, however, according to Kirchhoff’s law of radiation, the ratio of emissivity and absorption abilities does not depend on the nature of the body and is a universal function of frequency (wavelength) and temperature:

By definition, an absolutely black body absorbs all radiation incident on it, that is, for it. Therefore, the function coincides with the emissivity of an absolutely black body, described by Planck’s formula, as a result of which the emissivity of any body can be found based only on its absorption capacity.

Real bodies have an absorption capacity less than unity, and therefore an emissivity less than that of an absolutely black body. Bodies whose absorption capacity does not depend on frequency are called gray. Their spectrum has the same appearance as that of an absolutely black body. In the general case, the absorption capacity of bodies depends on frequency and temperature, and their spectrum can differ significantly from the spectrum of an absolutely black body. The study of the emissivity of different surfaces was first carried out by the Scottish scientist Leslie using his own invention - the Leslie cube.

In theoretical studies, it is more convenient to use the frequency function to characterize the spectral composition of equilibrium thermal radiation. In experimental work, it is more convenient to use the wavelength function. Both functions are related to each other by the formula

In astrophysics, Kirchhoff's law is often used in the following form:

where is the emissivity (energy emitted by a unit volume in a unit frequency interval per unit solid angle per unit time); — absorption coefficient taking into account stimulated emission (, where is the density of the substance, and and are, respectively, the opacity and the effective path length of photons for frequency ); — intensity of radiation of an absolutely black body.

Kirchhoff's law is valid only for cases of thermal equilibrium. However, it is often used for nonequilibrium systems, when the radiation is not in equilibrium with matter and its frequency distribution differs significantly from the Planck one. In this case, often (but not always) the assumption of thermodynamic equilibrium between the particles of the emitting substance turns out to be a good approximation. The degree of deviation from Kirchhoff's law can serve as a measure of the difference between the radiation of space objects and thermal radiation.

Physical formulas and calculation examples

Formulas for the equivalent resistances of a circuit consisting of a pair of resistors R 1 and R 2 can be divided into a certain series:

parallel connection is determined by the formula Req. = (R1*R2)/R1+R2;
sequential inclusion is calculated by determining its sum Req. = R1+R2.

The mixed connection of resistive elements does not have a specific formula. In order not to get confused during lengthy transformations, it is permissible to use a special program from the Internet. This is an “online calculator” service. It will help you understand complex connection diagrams, be it a triangle, square, pentagon or other schematic figure formed by resistive elements.

You can understand how all formulas and methods work using a specific problem. The first picture shown is a mixed electrical circuit. It includes 10 resistors. The elements are presented in the following denominations:

R1 = 1 Ohm;
R2 = 2 Ohm;
R3 = 3 Ohm;
R4 = 6 Ohm;
R5 = 9 Ohm;
R6 = 18 Ohm;
R7 = 2Ohm;
R8 = 2Ohm;
R9 = 8 Ohm;
R10 = 4 Ohm.

Voltage applied to the circuit:

U = 24 V.

It is required to calculate the currents on all resistive elements.

Source circuit

Ohm's law is used for calculations:

I = U/R, substituting the equivalent resistance for R.

Attention! To solve this problem, the total (equivalent) R is first calculated, after which the current in the circuit and the voltage on each resistive component are calculated.

By calculating Req., the given chain is divided into links containing parallel and serial connections. Calculations are made for each such link, and then for the entire chain.

The figure above shows a mixed resistance connection. It can be divided into three sections:

AB – a section with two parallel branches;
BC – a segment containing a sequential conjugation;
CD is a section of a circuit with an arrangement of three parallel chains.

Resistances R2 and R3, forming the lower branch of segment AB, are connected in series, which is taken into account in the calculation.

Series connected resistors R2 and R3

If you look at section CD, you can note the mixed inclusion of resistive elements.

Mixed inclusion on the CD section

The beginning of the calculations is to determine the equivalent resistances for these mixed fragments. Do this in the following order:

Req.2.3 = R2+R3=2 + 3 = 5 Ohm;
Req.7.8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ohm;
Reeq.7,8,9 = Reeq.7.8 + R9 = 1 + 8 = 9 Ohm.

Knowing the values of the obtained equivalents, the original circuit is simplified. It will look like the one shown in the figure below.

The result of the first coagulation

Next, you can determine Req. for sections AB , BC , CD , according to the formulas:

Req.AB = (R1*Req. 2.3)/R1 + Reeq. 2.3 = (1*5)/1 + 5 = 0.83 Ohm;
Req.BC = R4 + R5 = 6 + 9 = 15 Ohm;
1/Req.CD = 1/R6 + 1/Req.7,8.9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0.05 + 0.11 + 0.25 = 0, 41 Ohm.

As a result of the calculations performed, an equivalent circuit is obtained, which includes three Req. resistance. It looks like the one shown in the figure below.

Result of subsequent folding

Now you can determine the equivalent resistance of the entire original circuit by adding the equivalent values of all three sections:

Req. = Req.AB + Req.BC + Req.CD = 0.83 + 15 + 0.41 = 56.83 Ohm.

Next, using Ohm's law, find the current in the last serial section:

I = U/ Req. = 24/56.83 = 0.42 A.

Knowing the current strength, you can find what the voltage drop is in the considered sections AB, BC, CD. This is done as follows:

UAB = I* Req.AB= 0.42*0.83 = 0.35 V;
UBC = I* Reeq.BC = 0.42*15 = 6.3V;
UCD = I* Req.CD = 0.42*0.41 = 0.17 V.

The next step is to determine the currents on parallel segments AB and CD :

I1 = UAB/R1 = 0.35/1 = 0.35 A;
I2 = UAB/Req.2.3 = 0.35/5 = 0.07 A;
I3 = UCD/R6 = 0.17/18 = 0.009 A;
I6 = UCD/Req.7,8,9= 0.17/9 = 0.02 A;
I7 = UCD/R10 = 0.17/4 = 0.04 A.

Next, to find the values of the currents passing through R7 and R8, you need to calculate the voltage across these two resistors. First find the voltage drop across R9.

U9 = R9*I6 = 8*0.02 = 0.16 V.

Now the voltage falling on Req. 7.8 will be the difference between U CD and U9.

U7.8 = UCD – U9= 0.17 – 0.16 = 1 V.

After this, you can already find out the value of the currents moving through resistors R 7 and R 8, using the formulas:

I4 = U7.8/R7 = 1/2 = 0.5 A;
I5 = U7.8/R8 = 1/2 = 0.5 A.

Worth noticing! The current flowing through R4 and R5 is equal in value to the current in the segment that does not have a branch.

When calculating circuits and solving problems of finding the values of electrical parameters, it is necessary to use equivalent resistances. With the help of such a replacement, complex structures are transformed into elementary circuits, which are reduced to parallel and series connections of resistive elements.

Kirchhoff's law in chemistry

Kirchhoff's law states that the temperature coefficient of the thermal effect of a chemical reaction is equal to the change in the heat capacity of the system during the reaction.

Differential form of the law:

Integral form of the law:

where and are the isobaric and isochoric heat capacities, is the difference in the isobaric heat capacities of the reaction products and the starting substances, is the difference in the isochoric heat capacities of the reaction products and the starting substances, and and are the corresponding thermal effects.

If the difference is small, then we can accept and, accordingly, the integral form of the equations will take the following form:

With a large temperature difference, it is necessary to take into account the temperature dependences of the heat capacities: and