Mysterious quantum phenomena still surprise researchers with their unimaginable behavior. Earlier we talked about superfluidity, today we will consider another quantum mechanical phenomenon - superconductivity.
What is superconductivity? Superconductivity is a quantum phenomenon of the flow of electric current in a solid body without losses, that is, with strictly zero electrical resistance of the body.
Background
With the introduction of the concept of “absolute zero” into physics, scientists began to increasingly study the properties of substances at low temperatures, when there is practically no movement of molecules. To achieve low temperatures, a process called “gas liquefaction” is required. When evaporating, such a gas takes energy from the body that is immersed in this gas, since energy is required to separate molecules from the liquid. Similar processes occur in household refrigerators, where liquefied freon gas evaporates in the freezer.
At the end of the 19th and beginning of the 20th centuries, liquefied gases such as oxygen, nitrogen, and hydrogen were already produced. For a long time, helium could not be liquefied, but it was expected that it would help achieve a minimum temperature.
Heike Kamerlingh Onnes (right) with assistant Gerrit Flim (left)
Success in the liquefaction of helium was achieved by the Dutch physicist Heike Kamerlingh-Onnes in 1908, who worked at the University of Leiden (Netherlands). Liquefied helium made it possible to reach a record low temperature - about 4 K. Having received liquid helium, the scientist began to study the properties of various materials at helium temperatures.
Dependence of electrical resistance on temperature
The dependence of electrical resistance on the temperature of a substance was noticed back in the 19th century. As the temperature decreases, the thermal movement of the atoms of the crystal lattice of the conductor decreases; free electrons pass through it more easily, encountering less resistance.
Rice. 1. Dependence of resistance on temperature.
However, the dependence of resistance on temperature is linear only at not too low temperatures. First, although atomic nuclei are very small compared to electron orbits, the probability of collision with them is non-zero. And secondly, as the temperature decreases, electrons begin to bind more closely to the nuclei of atoms, the concentration of free electrons decreases, which should also increase electrical resistance.
It was possible to find out which process predominates at low temperatures only experimentally.
History of discovery
One of the questions that interested Kamerlingh Onnes was the study of the resistance of metals at ultra-low temperatures. It was known that as temperature increases, electrical resistance also increases. Therefore, we can expect that the opposite effect will be observed as the temperature decreases.
Experimenting with mercury in 1911, the scientist brought it to freezing and continued to lower the temperature. When 4.2 K was reached, the device stopped recording resistance. Onnes replaced the devices in the research facility because he was afraid they would malfunction, but the devices consistently showed zero resistance, despite the fact that absolute zero was still 4 K away.
After the discovery of superconductivity of mercury, a large number of questions arose. Among them: “is superconductivity characteristic of substances other than mercury?” or “the resistance drops to zero, or it is so small that existing devices cannot measure it.
Onnes proposed an original study that indirectly measured to what level resistance was reduced. The electric current excited in a semiconductor circuit, which was measured by deflecting a magnetic needle, did not die out for several years. According to the results of this experiment, the electrical resistivity of the superconductor obtained through calculations was 10−25 Ohm•m. Compared to the electrical resistivity of copper (1.5۰10−8 Ohm•m), this value is 7 orders of magnitude less, which makes it practically zero.
Characteristics of superconductivity
In superconducting materials, superconducting characteristics appear when the temperature T drops below the critical temperature Tc. The value of this critical temperature varies from material to material. Conventional superconductors typically have critical temperatures ranging from about 20 K to less than 1 K. For example, solid mercury has a critical temperature of 4.2 K.
As of 2015, the highest critical temperature found for a conventional superconductor is 203 K for H2S, although a high pressure of about 90 gigapascals was required. Cuprate superconductors can have much higher critical temperatures: YBa2Cu3O7, one of the first cuprate superconductors discovered, has a critical temperature of 92 K, and mercury-based cuprates with critical temperatures exceeding 130 K have been found.
The explanation for these high critical temperatures remains unknown. Electron pairing due to phonon exchanges explains superconductivity in conventional superconductors, but does not explain superconductivity in newer superconductors, which have a very high critical temperature.
Figure 4. Superconductors
Meissner effect
In addition to superconductivity, superconductors have another distinctive feature, namely the Meissner effect. This is the phenomenon of rapid decay of the magnetic field in a superconductor. A superconductor is diamagnetic, that is, in a magnetic field, macroscopic currents are induced in the superconductor, which create their own magnetic field, which completely compensates for the external one.
Magnet levitating above a high-temperature superconductor cooled by liquid nitrogen
The Meissner effect disappears in strong magnetic fields. Depending on the type of superconductor (more on this later), the superconducting state either disappears completely (type I superconductors), or the superconductor is segmented into normal and superconducting regions (type II). It is this effect that can explain the levitation of a superconductor above a strong magnet, or a magnet above a superconductor.
Temperature
In 1986, it was discovered that some cuprate-perovskite ceramic materials have a critical temperature above 90 K (−183 °C). Such a high transition temperature is theoretically impossible for a conventional superconductor, leading to the materials being called high-temperature superconductors.
Available refrigerant liquid nitrogen boils at 77 K, and thus superconductivity at higher temperatures than these facilitates many experiments and applications that are less practical at lower temperatures. This is the answer to the question at what temperature does the phenomenon of superconductivity occur.
Figure 3. Superconductivity
Meissner effect
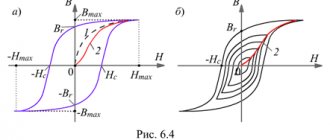
Surprisingly, until 1933, no researcher asked the question of the penetration of a magnetic field into a superconductor. Apparently, the answer seemed trivial and followed from the idea of a superconductor as a conductor with infinite conductivity σ = ∞. In accordance with these views, during the transition to a superconducting state, the magnetic field should remain the same as it was before the transition, or in other words, freeze. Indeed, from the material ratio
j = σE and the condition of finite current and infinite conductivity follows E = 0, from which, using Maxwell’s equation ∂B ∂t = −crotE, we instantly obtain ∂B ∂t = 0,
i.e. field B is constant in time, frozen. If we froze a superconductor in a zero field, and then turned on the field, we would get a picture of the field lines as in Fig. 4-(a), and if we cooled it in a finite field, then the field would not change, and the picture would be like Fig. 4- (b).The Austrian scientist Meissner suggested that the question of the penetration of a magnetic field into a superconductor is not entirely trivial and in 1933 he undertook experimental studies and discovered the effect that bears his name.
He discovered that regardless of whether a transition to a superconducting state occurs in a zero or finite field, in the final state of the intrasuperconductor there is always B = 0 and the picture of the field lines looks like shown in Fig. 4-(a). This is the content of the Meissner effect, from the superconductor to magnetic the field is pushed out and inside the superconductor there is a magnetic field B = 0. We can say that the superconductor is an ideal diamagnetic.
Theoretical explanation of the superconductivity effect
Phenomenological approach. Although Kamerlingh Onnes is the discoverer of superconductivity, the first theory of superconductivity was first proposed in 1935 by German physicists and brothers Fritz and Heinz London. Scientists sought to mathematically record such properties of a superconductor as superconductivity and the Meissner effect, without delving into the microscopic causes of superconductivity, phenomenologically. The derived equations made it possible to explain the Meissner effect in such a way that an external magnetic field could penetrate into a superconductor only to a certain depth, depending on the so-called London penetration depth. To explain superconductivity, it was necessary to assume that the current carriers in a superconductor, as in a metal, are electrons. At the same time, zero resistance means that the electron does not experience collisions during its movement. Since this applies to all conduction electrons, there is a current of electrons without resistance.
Obviously, this theory does not explain the very nature of this phenomenon, but only describes it and allows us to predict its behavior in a number of cases. A deeper, but also phenomenological theory was proposed in 1950 by Soviet theoretical physicists Lev Landau and Vitaly Gnizburg.
A Cooper pair of electrons moving through a lattice of positive atoms. The first electron distorts the lattice, creating a region of increased positive charge into which the second electron is drawn.
BCS theory. The first qualitative explanation of the phenomenon of superconductivity was proposed within the framework of the so-called BCS theory, constructed by American physicists John Bardeen, Leon Cooper and John Schrieffer. This theory comes from the assumption that attraction can arise between electrons under certain conditions. Attraction, which is caused by various excitations, primarily by vibrations of the crystal lattice, is capable of creating “Cooper pairs” - bound states of two electrons in a crystal. Such a pair can move in a crystal without being scattered either by vibrations of the crystal lattice or by impurities. In substances with a temperature far from zero, there is enough energy to “break” such a pair of electrons, while at low temperatures the system does not have sufficient energy. As a result, a flow of bound electrons - Cooper pairs - appears, which practically do not interact with the substance. In 1972, D. Bardeen, L. Cooper and D. Schrieffer received the Nobel Prize in Physics.
Later, the Soviet theoretical physicist Nikolai Bogolyubov improved the BCS theory. In his works, the scientist described in detail the conditions under which Cooper pairs can be formed (energy close to the Fermi energy, certain spins, etc.) as a result of quantum effects. Individually, electrons are particles with half-integer spin (fermions) that are unable to form a Bose-Einstein condensate and become superfluid. When there is a Cooper pair of electrons, then it represents a quasiparticle with integer spin and is a boson. Under certain conditions, bosons are capable of forming a Bose-Einstein condensate, that is, a substance whose particles occupy the same state, which leads to the occurrence of superfluidity. This superfluidity of electrons explains the effect of superconductivity.
Properties of superconductors
Most of the physical properties of superconductors vary from material to material, such as heat capacity and critical temperature, critical field, and critical current density at which superconductivity breaks down. On the other hand, there is a class of properties that do not depend on the base material.
For example, all superconductors have absolutely zero resistivity at low applied currents, when there is no magnetic field or when the applied field does not exceed a critical value. The presence of these universal properties implies that superconductivity is a thermodynamic phase and therefore has certain distinctive properties that are largely independent of microscopic details .
The situation is different in a superconductor. In a conventional superconductor, the electron liquid cannot be separated into individual electrons. Instead, it consists of bonded pairs of electrons known as Cooper pairs. This pairing is caused by the attractive force between electrons resulting from the exchange of phonons.
Due to quantum mechanics, the energy spectrum of this Cooper pair fluid has an energy gap, meaning there is a minimum amount of energy ΔE that must be supplied to excite the fluid. Therefore, if ΔE is greater than the thermal energy of the lattice, given by kT, where k is Boltzmann's constant and T is the temperature, the liquid will not be dissipated by the lattice. Thus, the Cooper vapor fluid is superfluid, meaning that it can flow without dissipating energy.
Superconductors in an alternating electric field
In addition to superconductivity and the Meissner effect, superconductors have a number of other properties. It is worth noting the following - zero resistance of superconductors is characteristic only at constant current. An alternating electric field makes the resistance of the superconductor non-zero and it increases with increasing field frequency.
Just as the two-fluid model divides a superfluid material into a region of superfluidity and a region of ordinary matter, so the flow of electrons is also divided into superconducting and ordinary. A constant field would accelerate superconducting electrons to infinity (given their zero resistance), which is impossible, because it turns to zero when they hit the superconductor. Since a constant electric field does not act on superconductors, ordinary electrons are not affected by it (it is simply pushed out), which means that the movement is represented only by superconducting electrons.
In the case of an alternating electric field, the process of acceleration of electrons occurs followed by deceleration, which is physically possible. In this case, there is also a current of ordinary electrons, which have the property of resistance. The higher the frequency of such a field, the greater the effects associated with ordinary electrons.
Applications of superconductors
Are you an expert in this subject area?
We invite you to become the author of the Directory Working Conditions The use of superconductors is very diverse. With their help, you can obtain large currents using a source that has a low voltage. At the same time, there are practically no losses due to Joule heat, which makes it possible to use the superconductor in measuring instruments. Thus, the sensitivity of a galvanometer with a frame made of a superconductor is very high ($\sim {10}^{-12}B$).
Currently, due to the resistance of the supply wires, electricity losses amount to $30-40\%$. If it became possible to transmit electricity through superconducting wires, then there would be no loss of Joule heat, which would be equivalent to an increase in electricity generation by a third. Based on superconductors, it would be possible to produce generators and electric motors with much higher efficiency than those currently existing.
High-current technologies, which are intended for high-power devices, are used in the electric power industry, industry and transport. In these industries, superconducting technologies lead to the creation of electrical equipment that is $2-3 times lighter, more environmentally friendly, more reliable and has a longer service life. It is expected that in the electric power industry there will be a gradual replacement of traditional resistor equipment with cheaper and more compact superconductor equipment, which is significantly higher in reliability and efficiency.
London moment
Another interesting property of a superconductor is the London moment. The essence of the phenomenon is that a rotating superconductor creates a magnetic field that is aligned exactly along the axis of rotation of the conductor.
Further study of this phenomenon led to the discovery of London's gravity magnetic moment. In 2006, researchers Martin Tajmar from the ARC Seibersdorf Research Institute, Austria, and Clovis de Matos from the European Space Agency (ESA) discovered that a spinning superconductor also generates a gravitational field. However, such a gravitational field is approximately 100 million times weaker than the earth's.
Classification of superconductors
There are several classifications of superconductors, which are based on the following criteria:
- Response to a magnetic field. This property divides superconductors into two categories. Type I superconductors have a certain critical magnetic field value, exceeding which they lose superconductivity. Type II - have two limiting values of the magnetic field. When a magnetic field limited to these values is applied to superconductors in this category, the field partially penetrates while maintaining superconductivity.
- Critical temperature. There are low-temperature and high-temperature superconductors. The former have the property of superconductivity at temperatures below −196 °C or 77 K. High-temperature superconductors require a temperature higher than this. This division occurs because high-temperature superconductors can be used in practice as coolers.
- Material. Here there are such varieties as: pure chemical element (like mercury or lead), alloys, ceramics, organic or iron-based.
- Theoretical description. As is known, any physical theory has a certain scope of application. For this reason, for further application, it makes sense to divide superconductors according to theories that can describe their nature.
Description. Superconductivity phenomenon:
Superconductivity is the property of some materials to have absolutely zero electrical resistance when they reach a temperature below a certain value (the so-called critical temperature).
Metals and their alloys, semiconductors, as well as ceramic materials and other substances possess superconductivity There are even superconducting alloys and materials in which one of the elements or all the elements included in its composition may not be superconductors. For example, hydrogen sulfide, alloys of mercury with gold and tin.
The superconducting state in the material does not appear gradually, but abruptly - when the temperature reaches below the critical one. Above this temperature, the metal, alloy or other material is in a normal state, and below it - in a superconducting state. For some substances, the transition to the superconducting state becomes possible under certain external conditions, for example, upon reaching a certain pressure value.
Superconductivity as a phenomenon is accompanied by several effects. Two of them are of decisive importance: the disappearance of electrical resistance and the expulsion of the magnetic flux (field) from its volume. Therefore, not only the critical current, but also the critical magnetic field—a certain value of the magnetic field strength, upon reaching which the superconductor loses its superconductivity property—is of utmost importance.
The phenomenon of superconductivity can be demonstrated in practice. If you take a conductor, loop it, making a closed electrical circuit, cool it to a temperature below critical and supply electric current to it, and then remove the source of electric current, then the electric current in such a conductor will exist for an unlimited time.
Currently, superconductors have been obtained that have the property of superconductivity at room temperature .
Superconductivity of graphene
Over the past few years, graphene's popularity has increased significantly. Let us recall that graphene is a layer of modified carbon, one atom thick. First of all, this was facilitated by the discovery of carbon nanotubes - a specific ultra-strong material that is created by folding one or several layers of graphene.
Large-scale simulation of a structure formed when one graphene lattice is rotated at a "magic angle" relative to a second graphene lattice
In 2018, a group of researchers from the Massachusetts Institute of Technology and Harvard University, led by Professor Pablo Jarillo-Herrero, discovered that when rotated at a certain (“magical”) angle, two sheets of graphene are completely devoid of electrical conductivity. When the researchers applied a voltage to the material by adding a small number of electrodes to this graphene structure, they found that at a certain level, electrons broke free of their original insulating state and flowed without resistance. The most important feature of this phenomenon is that the superconductivity of the specified graphene structure was obtained at room temperature. And although the explanation for this effect is still in question, its potential in the energy supply sector is quite high.
Applications of Superconductivity
Strong magnetic fields are just one of many possible and partly realized uses of superconductivity. The most precise instruments of physical experimentation - superconducting galvanometers and radiation detectors, resonators with a superconducting coating for microwave technology and for linear accelerators of heavy particles, magnetic lenses for electronic
microscopes, electric motors on frictionless superconducting bearings, lossless transformers and transmission lines, magnetic screens, energy accumulators, and finally, miniature and high-speed “memory cells” of computers - this is a greatly reduced list of problems of today's applied superconductivity.
They are already saying that all classical electrical engineering can be “reinvented” if it is built not on ordinary conductors of electric current, but on superconducting materials.
Well, what if you dream a little? After all, in space there are ideal conditions for the operation of superconducting devices, ideal conditions for superconductivity. In the vacuum of outer space, a body can be heated from the outside only due to radiation (from the Sun, for example). If so, then any opaque screen is sufficient, and any object in space is completely thermally insulated. And since the elements of our imaginary machine themselves are superconducting and current flows through them without resistance, heat is not generated in them. Liquid helium
There will be almost no evaporation, which means that the device will be able to operate indefinitely. Remember the experience of Collins, whose lead steering wheel retained current for almost three years.
Can you imagine that somewhere in orbit around the Moon there is a kind of cryogenic computer rotating, one serving entire sectors of the earth’s economy, science and transport? And what about superconducting magnets—maybe they will be the ones that will hold the plasma in the thermonuclear reactors of the future? Or cooled electrical cables, through which electrical energy can be transmitted over tens of thousands of kilometers without any loss?
Is this fantasy? Everything that has been said here is possible in principle. So it will be done. But when?
This is an excellent area both for imagination and for deep theoretical and experimental work.
In the meantime, the niobium-tin alloy remains the only substance with a maximum critical temperature of minus 254.8 degrees, and no one can understand for what advantages nature has distinguished it from thousands of other inorganic substances. No additions of other elements, no changes in the internal structure of this alloy could increase its critical temperature. The search for other, similar, double and triple alloys also turned out to be unsuccessful - no one has ever managed to rise above this enchanted number - minus 254.8 degrees. They began to say that, apparently, this temperature was not accidental; it was probably a limit that could not be crossed. All that remains is to find a theoretical justification for this fact, to find the reason why superconductivity cannot exist in metal systems at higher temperatures.
Author: Pavel Chaika, editor-in-chief of Poznavaika magazine
When writing the article, I tried to make it as interesting, useful and high-quality as possible. I would be grateful for any feedback and constructive criticism in the form of comments on the article. You can also write your wish/question/suggestion to my email [email protected] or Facebook, with respect, the author.
Author page