Operating principle
This phenomenon is observed when a system is able to store and easily transfer energy between two or more different storage modes, such as kinetic and potential energy. However, there is some loss from cycle to cycle, called attenuation. When the damping is negligible, the resonant frequency is approximately equal to the natural frequency of the system, which is the frequency of unforced oscillation.
These phenomena occur with all types of oscillations or waves: mechanical, acoustic, electromagnetic, nuclear magnetic (NMR), electron spin (ESR), and quantum wave function resonance. Such systems can be used to generate vibrations of a certain frequency (for example, musical instruments).
The term "resonance" (from the Latin resonantia, "echo") comes from the field of acoustics, especially seen in musical instruments, such as when strings begin to vibrate and produce sound without direct input from the player.
ELECTRONIC PARAMAGNETIC RESONANCE
ELECTRONIC PARAMAGNETIC RESONANCE (EPR), resonant absorption of electromagnetic energy by substances containing paramagnetic particles. Paramagnetic are particles that have a magnetic moment - atoms and molecules with an odd number of electrons (for example, N, H atoms, NO molecule); free radicals (eg H3); ions with partially filled internal shells (for example, ions of transition elements); color centers in crystals; conduction electrons in metals and semiconductors; superparamagnetic nanoparticles formed by dissolution or in alloys with a collective magnetic moment that behave like an electron gas. EPR is one of the radiospectroscopy methods; usually observed in the milli- and centimeter wavelength ranges (2–30 mm) and is a special case of magnetic resonance. Discovered by E.K. Zavoisky in 1944.
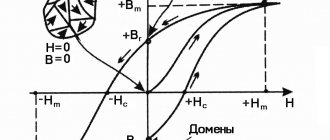
Spatial quantization of spins S in a magnetic field H and splitting of energy levels: a – free electron; b and c – paramagnetic particles with several electrons with spin S=1 and S=5/2 with...
In a constant magnetic field of strength H , the energy levels of a paramagnetic particle with spin S and magnetic moment μ, due to spatial quantization, are split into 2S+1 magnetic sublevels that differ in energy by Δℰ=2μH (see Zeeman effect). In the case of a free electron (Fig., a) S=1/2, magnetic moment μ=gSμBMS, where gS≈2 (g-factor of a free electron), μB – Bohr magneton, MS=±1/2 (magnetic quantum number) . In the field H, the energy ℰ of an electron can take 2 values: ℰ1=-1/2gSμБH and ℰ2=+1/2gSμБH. Transitions between magnetic sublevels are possible if the electromagnetic energy quantum ћω (ω – frequency, ћ – Planck’s constant) is equal to Δℰ, i.e. ћω=Δℰ=gSμБH, while a simultaneous change in spin direction ΔMS=±1 occurs. When moving from a lower level to an upper one, energy is absorbed, and when going back, it is emitted. The probability of these processes is the same, but since under thermodynamic conditions. equilibrium, according to the Boltzmann distribution, the population of the lower level is greater than that of the upper level, then energy is absorbed.
For particles containing several electrons, S can take any multiple of 1/2 value (Fig., b and c), and the energy of the levels ℰ=gμБMSH, where MS can have (2S+1) values. The value of the g-factor is determined by the total value of the spin and orbital angular momentum of the electron and can be several. times different from gS. Between levels that differ in MS by ΔMS=±1, magnetic dipole transitions are possible, and the resonance condition will still be ћω=Δℰ=gSμБH.
Interaction of electrons with electricity. intracrystalline field for S⩾1 leads to splitting of energy levels with decomposition. values of ∣MS∣. As a result, several appears in the EPR spectrum. absorption lines (fine structure). The interaction of electrons with the magnetic moment of the nucleus of a paramagnetic atom leads to the appearance of a hyperfine structure in the EPR spectrum, and the interaction of electrons with the magnetic moments of the nuclei of surrounding ions leads to a superfine structure; their study allows us to determine the location of unpaired electrons.
Relaxation processes that restore equilibrium in the system of electron spins, disturbed as a result of the absorption of electromagnetic energy, are characterized by relaxation times T1 and T2. The EPR linewidth Δω=1/T1+1/T2, where T1 is the spin-lattice relaxation time, characterizes the rate of restoration of equilibrium between the spin system and the lattice, and is determined by the interaction of the magnetic moments of particles with crystalline vibrations. grates, when the temperature decreases, it increases; T2 is the spin-spin relaxation time, characterizes the rate of restoration of equilibrium in the spin system and is practically independent of temperature.
To measure EPR, radio spectrometers (EPR spectrometers) are used, in which, at a constant frequency and a slow change in the magnetic field, a change in the power absorbed in the sample is recorded. The EPR spectra of transition metal ions are the most well studied. Measurements are carried out on single crystals, which are diamagnetic dielectrics, into which impurities (0.001–0.1%) of paramagnetic ions are introduced. Symmetry intracrystalline. The field determines the symmetry of the g-factor and the constants of fine and hyperfine interactions, and its intensity determines their magnitude. EPR - main method for studying free radicals in condensers. environments
EPR is widely used in various fields of physics, chemistry, geology, biology, medicine. Intensively used to study the surface of solids and semiconductors, phase transitions, disordered systems, enzymes and free radicals in biology. systems, in radiation and photochemistry, in catalysis.
Examples of resonance in life
Pushing a person on a swing is a common example of this phenomenon. A loaded swing, a pendulum, has a natural vibration frequency and a resonant frequency that resists being pushed faster or slower.
An example is the oscillation of projectiles on a playground, which acts like a pendulum. A person's push while swinging at a natural swing interval causes the swing to go higher and higher (maximum amplitude), while attempting to swing at a faster or slower pace creates smaller arcs. This is because the energy absorbed by vibrations increases when the shocks correspond to natural vibrations.
The response is widely found in nature and is used in many artificial devices. This is the mechanism by which virtually all sine waves and vibrations are generated. Many of the sounds we hear, such as when hard objects made of metal, glass or wood hit, are caused by short vibrations in the object. Light and other short-wave electromagnetic radiation is created by resonance on the atomic scale, such as electrons in atoms. Other conditions in which the beneficial properties of this phenomenon may apply:
- Timekeeping mechanisms of modern watches, a balance wheel in a mechanical watch and a quartz crystal in a watch.
- Tidal response of the Bay of Fundy.
- Acoustic resonances of musical instruments and the human vocal tract.
- Destruction of a crystal glass under the influence of a musical right tone.
- Frictional idiophones, such as making a glass object (glass, bottle, vase), vibrate when rubbed around its edge with a fingertip.
- The electrical response of tuned circuits in radios and televisions that allow selective reception of radio frequencies.
- Creation of coherent light by optical resonance in a laser cavity.
- Orbital response, exemplified by some of the gas giant moons of the Solar System.
Atomic-scale material resonances are the basis of several spectroscopic techniques that are used in condensed matter physics, for example:
- Electronic spin.
- Mossbauer effect.
- Nuclear magnetic.
Forced vibrations. Resonance
This topic is devoted to forced oscillations and resonance.
Earlier we talked about oscillatory motion and harmonic oscillations. Harmonic
are called oscillations in which the displacement of an oscillating material point occurs according to the law of sine or cosine.
It is known that real vibrations do not occur exactly according to the harmonic law
. Not a single oscillatory process in nature or technology continues indefinitely, but has a beginning and an end in time. And the oscillatory process, limited in time, is not harmonic.
But in nature there are oscillatory processes that occur over a very long time. An example of this type of oscillation is the periodic changes in voltage between different parts of the human body that arise as a result of the work of the heart. A graph of the voltage “produced” by the heart muscle versus time is called an electrocardiogram.
.
As can be seen from the figure, it is very little similar to a sine wave. That is, the oscillations of biocurrents are non-harmonic
.
However, as theoretical calculations show, any periodic oscillation can be mathematically represented as a sum of harmonic oscillations of multiple frequencies, and the amplitudes of the harmonics of this series (Fourier series) decrease with increasing number.
Also previously considered were mathematical and spring pendulums, the oscillations of which were taken to be harmonic. However, in fact, the oscillations of pendulums are only close to harmonic, but are not so
, since air resistance and irreversible energy losses due to heating of the thread and spring during their deformation also lead to the fact that the amplitude of oscillations decreases over time.
Oscillations whose amplitude decreases over time are called damped
.
Since free oscillations always die out over a certain period of time, they do not find practical application. The simplest way to excite undamped oscillations is to act on an oscillatory system with an external periodic force, exciting oscillations that the system itself would not perform.
The work of this external force on the system provides an influx of energy to it from the outside, which does not allow the oscillations to die out, despite the action of resistance forces.
Such oscillations, that is, oscillations occurring under the influence of an external periodic force, are called forced
oscillations
.
The main difference between forced oscillations and free ones
is that during free oscillations the system receives energy only once, when it is removed from the equilibrium position, and during forced oscillations the energy is constantly replenished due to the work of the driving force.
Initially, in the process of establishing forced oscillations, they are of a complex nature: a superposition of free damped as well as forced oscillations occurs. And only after free vibrations stop, only forced vibrations remain.
Let us consider some features of forced oscillations.
1) External influence imposes its own law of oscillations on the system
: so, if the value of the external force changes according to the law of sine (or cosine), then the forced oscillations will be harmonic. Note that there is a phase difference between forced oscillations and external force oscillations.
where j
– phase difference.
2) H
The frequency of forced oscillations is equal to the frequency of change of the driving force.
3) Amplitude of forced oscillations
the greater the amplitude of the driving force.
4) Amplitude of forced oscillations
depends on the frequency of the forcing influence, it reaches its maximum value when the frequency of forced oscillations coincides with the natural frequency, that is, with the frequency of free oscillations of the system. When the frequency of the driving force approaches the natural frequency of oscillations of the system, the amplitude of oscillations increases, and at higher frequencies it decreases.
The phenomenon of a sharp increase in the amplitude of forced oscillations, when the frequency of the driving force is close to the frequency of natural oscillations of the system, is called mechanical
resonance
.
The frequency at which the amplitude of forced oscillations is maximum is called resonant
.
And the graph of the dependence of the amplitude of forced oscillations on frequency is called a resonance
curve
.
The phenomenon of resonance is of great practical importance, as it is used to amplify various vibrations in technology.
For example, forced vibrations are used when operating vibration devices
for compacting loose base under foundations and roads, compacting concrete when pouring foundations. Vibrators are also used for vibratory driving of piles and pipes, vibratory placement of concrete, and sorting of bulk materials.
But mechanical resonance can also cause destruction of the oscillatory system
, if the amplitude of forced oscillations exceeds certain limits.
Therefore, for example, the engine in a car is installed on special shock absorbers, in which the mechanical vibration energy is damped and converted into heat.
In buildings, vibrating units (such as electric motors, diesel units) are placed on rubber or metal shock absorbers. Otherwise, a sharp increase in the amplitude of vibrations during resonance can cause destruction of structures.
Resonance phenomena are also possible in other structures. For example, on April 16, 1850, near the city of Angers in France, on the Bas-Chêne suspension bridge, while a battalion of French troops was moving across the bridge during a strong wind, the first “resonance catastrophe” occurred. Despite the command given to slow down, the soldiers unintentionally moved in unison in an attempt to maintain balance on the wind-swayed bridge, which likely led to an increase in the amplitude of the vibrations and further collapse of the bridge. The collapse killed 226 people.
5) Amplitude depends on friction force
.
It decreases with increasing friction force, and the resonance curves become flatter (they say that there is a sharp
or
blunt resonance
).
If the friction force is very small, then the amplitude of forced oscillations, as calculations show, is directly proportional to the square of the amplitude of the external periodic force, and inversely proportional to the difference in the squares of the cyclic frequencies of free and forced oscillations of the system.
It is clear from the formula that as the frequency of forced oscillations tends to the frequency of free oscillations, the amplitude of forced oscillations tends to infinity.
Among various types of oscillatory movements, self-oscillations can also be distinguished. Self-oscillations
are called undamped oscillations in a system, supported by internal energy sources in the absence of the influence of an external variable force.
The term self-oscillations was first introduced into Russian terminology by the Soviet physicist Alexander Aleksandrovich Andronov in 1928.
Examples of self-oscillating systems include electric bells, internal combustion engines, clocks with weights, and so on.
What is common between self-oscillations and free oscillations
is that their
frequency and amplitude are determined by the properties of the oscillatory system itself
.
And the difference between self-oscillations and free damped oscillations
is that their
amplitude does not depend on time and on the initial short-term impact that excites the oscillatory process
.
As a rule, a self-oscillating system consists of three main parts: oscillatory system V; energy source S; and a feedback device B that regulates the flow of energy from the source to the oscillatory system R.
The simplest mechanical self-oscillating system is a pendulum clock with weights. In this clock the oscillatory system is a pendulum; the source of energy is the potential energy of a raised weight; and the feedback device is a ratchet wheel and an anchor. Loss of mechanical energy due to friction during movement is replenished by reducing the potential energy released with each oscillation of the pendulum of the weight clock.
Main conclusions:
We remembered what oscillations are called forced. We examined the features of forced oscillations. We remembered the phenomenon of mechanical resonance. We also talked about self-oscillations and self-oscillating systems.
Types of phenomenon
In describing resonance, G. Galileo drew attention to the most essential thing - the ability of a mechanical oscillatory system (heavy pendulum) to accumulate energy, which is supplied from an external source with a certain frequency. Manifestations of resonance have certain characteristics in different systems and therefore different types are distinguished.
Mechanical and acoustic
Mechanical resonance is the tendency of a mechanical system to absorb more energy when its vibration frequency matches the system's natural vibration frequency. This can lead to severe motion fluctuations and even catastrophic failure in unfinished structures, including bridges, buildings, trains and airplanes. When designing facilities, engineers must ensure that the mechanical resonant frequencies of component parts do not match the oscillatory frequencies of motors or other oscillating parts to avoid a phenomenon known as resonant disaster.
Electrical resonance
Occurs in an electrical circuit at a certain resonant frequency when the circuit impedance is minimum in a series circuit or maximum in a parallel circuit. Resonance in circuits is used to transmit and receive wireless communications such as television, cellular, or radio.
Optical resonance
An optical cavity, also called an optical resonator, is a special arrangement of mirrors that forms a standing wave resonator for light waves . Optical cavities are the main component of lasers, surrounding the amplification medium and providing feedback to the laser radiation. They are also used in optical parametric oscillators and some interferometers.
Light confined within the cavity produces standing waves repeatedly for specific resonant frequencies. The resulting standing wave patterns are called "modes". Longitudinal modes differ only in frequency, while transverse modes differ for different frequencies and have different intensity patterns across the beam cross section. Ring resonators and whispering galleries are examples of optical resonators that do not produce standing waves.
Orbital wobble
In space mechanics, an orbital response occurs when two orbiting bodies exert a regular, periodic gravitational influence on each other. This is usually because their orbital periods are related by the ratio of two small integers. Orbital resonances significantly enhance the mutual gravitational influence of bodies. In most cases, this results in an unstable interaction in which the bodies exchange momentum and displacement until resonance no longer exists.
Under some circumstances, a resonant system can be stable and self-correcting to keep bodies in resonance. Examples are the 1:2:4 resonance of Jupiter's moons Ganymede, Europa and Io and the 2:3 resonance between Pluto and Neptune. Unstable resonances with Saturn's inner moons create gaps in Saturn's rings. A special case of 1:1 resonance (between bodies with similar orbital radii) causes large Solar System bodies to clear out the neighborhoods around their orbits, pushing out almost everything else around them.
Atomic, partial and molecular
Nuclear Magnetic Resonance (NMR) is the name given to the physical resonance phenomenon associated with the observation of specific quantum mechanical magnetic properties of an atomic nucleus when an external magnetic field is present. Many scientific methods use NMR phenomena to study molecular physics, crystals, and non-crystalline materials. NMR is also commonly used in modern medical imaging techniques such as magnetic resonance imaging (MRI).
Organized himself
self-organizing systems can also exhibit a number of unusual properties.
, in which ordering occurs on the nano- and microscale.
(ILs). In the simplest case we are talking about molten salts, but in general the spectrum of ILs is quite wide and covers numerous combinations of organic and inorganic cations and anions. The range of their amazing physicochemical properties (primarily nano- and microheterogeneity) is also diverse, which can find application in a variety of fields of science and industry: from catalysis to biomedicine.
To date, many different types of nanostructures formed in ILs have been discovered, mainly theoretically: ion pairs, substructures based on hydrogen bonds, ion clusters, micelles-like nanostructures, sponge-like arrays of micrometer-scale nanostructures. However, many of the results of theoretical modeling are quite difficult to confirm experimentally.
In most cases, ILs are diamagnetic and therefore cannot be studied in their “pure form” using the EPR method. To do this, a special paramagnetic spin probe should be dissolved in them (usually in trace amounts).
This approach has its advantages and disadvantages. On the one hand, the probe molecules themselves, dissolved in pure IL, can specifically interact with the solvent. On the other hand, if even trace amounts of water (tens of parts per million!) are present in an IL, then its system of hydrogen bonds can change greatly, which will significantly affect the physicochemical properties. In addition, the question always arises: are the observed inhomogeneities in an IL inherent specifically to it or are they a consequence of the presence of a guest molecule in it?
However, since in any case most of the applications of ILs are somehow related to their role as a solvent, the interactions in the solvent–solute pair are quite natural. In this sense, the use of spectroscopic methods using probe molecules is completely justified, and by selecting the structure of the probe, it is possible to simulate real interactions of ILs with specific substances. For this reason, in the laboratory of EPR spectroscopy, three variants of EPR techniques using spin probes were used to study the heterogeneous structure of ILs.
the stationary EPR method
The spectra of probes played by stable radicals were analyzed. It turned out that for a series of ILs in the temperature range 170–270 K, the experimental spectrum corresponds to a superposition of two different fractions of spin probe molecules with a fundamentally different model of motion. One fraction consists of rotating molecules, the other - of sedentary ones. This suggests that the softening and melting of ILs at the molecular level is a fairly smooth process.
In the EPR method with time resolution
Photoexcited molecules such as porphyrins or fullerenes were used as spin probes.
Their ground state is diamagnetic, but when irradiated with light they transform into long-lived triplet states
*, which can be detected using ESR.
It turned out that such probe molecules are present in ILs in the form of several different fractions with different microenvironments and, accordingly, physical properties. It can be assumed that such heterogeneity is associated with the formation of nanosized cavities, similar to micelles, in ILs. the spin polarization lifetime was noted
(non-equilibrium population of energy levels) in ILs compared to traditional solvents, which may be useful for some applications.
Pulse EPR
involves the use of a pulsed microwave field and is used in different versions, using specific pulse sequences, often in combination with additional radio frequency excitation of the sample.
In the laboratory, this method was used to analyze random molecular librations
(low-angle “jitters”) of stable radicals used as spin probes - such movements effectively shorten the spin relaxation time.
In particular, using this approach, a density anomaly was discovered for the first time for glassy ILs. It turned out that in the temperature range of 150–200 K the mobility of probe molecules progressively decreases with increasing temperature, which contradicts all known trends.
This behavior can be described by nanoscale structural rearrangements, during which the ensemble of radicals in the IL matrix breaks down into two subgroups. Radicals located in the region of low density of the IL matrix begin to experience diffusion rotation, which is detected using stationary ESR, and those localized in other regions with increased density are detected using pulsed EPR. And although the average density of the IL remains constant, thanks to the selectivity of the techniques, it is possible to detect local density inhomogeneities that change with temperature up to the phase transition at the glass transition point.
It is interesting that such anomalies are observed not only in pure ILs, but also in their mixtures with water, which may be important, for example, in the development of new types of cryoprotectors.
The benefits and harms of resonance
In order to draw some conclusion about the pros and cons of resonance, it is necessary to consider in which cases it can manifest itself most actively and noticeably for human activity.
Positive effect
The response phenomenon is widely used in science and technology . For example, the operation of many radio circuits and devices is based on this phenomenon.
- Two-stroke engine. The muffler of a two-stroke engine has a special shape designed to create a resonant phenomenon. It improves engine performance by reducing consumption and pollution. This resonance partially reduces the unburned gases and increases compression in the cylinder.
- Musical instruments. In the case of string and wind instruments, sound production occurs mainly when the oscillatory system (strings, columns of air) is excited until the phenomenon of resonance occurs.
- Radios. Each radio station emits an electromagnetic wave with a clearly defined frequency. To capture it, the RLC circuit is forcibly vibrated by an antenna, which captures all electromagnetic waves that reach it. To listen to one station, the natural frequency of the RLC circuit must be tuned to the frequency of the desired transmitter by changing the capacitance of the variable capacitor (the operation is performed by pressing the station search button). All radio communication systems, whether transmitters or receivers, use resonators to "filter" the frequencies of the signals they process.
- Magnetic resonance imaging (MRI). In 1946, two Americans, Felix Bloch and Edward Mills Purcell, independently discovered the phenomenon of nuclear magnetic resonance, also called NMR, which earned them the Nobel Prize in Physics.
Negative impact
However, the phenomenon is not always useful . You can often find references to cases where suspension bridges broke when soldiers walked across them “in step.” At the same time, they refer to the manifestation of the resonant effect of resonance, and the fight against it becomes large-scale.
- Motor transport. Motorists are often annoyed by noise that occurs at certain vehicle speeds or as a result of engine operation. Some slightly rounded parts of the body resonate and emit sound vibrations. The car itself, with its suspension system, is an oscillator, equipped with effective shock absorbers that prevent sharp resonance from occurring.
- Bridges. The bridge can perform vertical and transverse vibrations. Each of these types of oscillations has its own period. If the lines are suspended, the system has a very different resonant frequency.
- Building. Tall buildings are susceptible to earthquakes. Some passive devices help protect them: they are oscillators whose natural frequency is close to the frequency of the building itself. Thus, the energy is completely absorbed by the pendulum, preventing the destruction of the building.
In pores and frameworks
Porous media, such as zeolites, are today actively used in various fields of chemistry, especially in heterogeneous catalysis. In the last two decades, the minds of researchers have been occupied by a new type of porous media - metal-organic
(MOC), capable of holding atoms and molecules of various substances within its structure.
MOFs can be easily prepared from coordination compounds that are formed by self-assembly of metal ions and organic ligands. This class of materials has broad capabilities for “fine-tuning” the structure and functions of the framework for a specific task by changing the pore size and structure of the active metal center. These potential “materials of the future” can be used to bind and store carbon dioxide and other gases, capture harmful impurities from air and water, convert solar energy, and even “targeted” delivery of drugs in the body.
From this point of view, the IOC design looks extremely attractive, but its implementation is not so simple. The most difficult thing is to determine how certain changes in the process of “tuning” the MOF will affect its properties.
It is especially difficult to take into account the influence of the degree of mobility (“flexibility”) of the structural elements of the framework on its ability to absorb various molecules. Imagine that we are designing a garage for a vehicle and choosing the dimensions of the beams and gates in such a way that it is convenient to park the car. And suddenly it turns out that depending on the air temperature, the size of the doorway can be reduced by almost half. Of course, in this case, we absolutely need to know exactly how the size of the opening depends on external conditions. Similar situations often occur in practical applications of flexible MOFs.
Most MOFs are diamagnetic; therefore, as in the case of ILs, when studying them using ESR, it becomes necessary to use paramagnetic spin probes. They can be molecules that are able to fit inside the framework structure without introducing significant disturbances into it (for example, an organic radical or a paramagnetic metal ion).
Recently, the EPR spectroscopy laboratory developed a method for introducing a paramagnetic spin probe into the cavity of a flexible ZIF-8 MOF. This frame, widely known among specialists, consists of large cavities connected by smaller “windows”, and thanks to a set of unique properties, it is a promising material for the sorption and separation of various substances. An example is the separation of a mixture of propane and propylene, which is an important technological task, since propylene is used to produce widely demanded polyethylene. The high efficiency of this separation is ensured by fine-tuning the size of the ZIF-8 cavity windows. However, little was known about the actual “effective” size of these cavity windows until recently.
When analyzing the EPR spectra of the spin probe located inside the ZIF-8 cavity, it turned out that it is extremely sensitive to atmospheric oxygen filling the pores. By immersing the frame in liquid, you can observe how it is filled, and by varying the solvents, you can determine which of them fit into the cavities and which do not. In addition, based on data on the rate of filling of cavities, it is possible to estimate the rate of diffusion of molecules into the frame.
As a result, using a series of solvents, it was possible to determine the real size of the ZIF-8 cavity windows and, moreover, to find out that it depends quite strongly on temperature. At temperatures around 90 °C, the size of the windows increases sharply, which fundamentally changes the permeability of this MOF to molecules.
As a result, using the example of separating a mixture of three xylenes (an important technological problem, since one of the xylenes is the initial monomer for the production of polyethylene terephthalate (PET), a popular thermoplastic), an approach was developed that allows us to isolate each of the components of the mixture by varying the temperature of the sorbent.
In the case of MOFs, there are situations when one of its structural elements (metal ion or ligand) is itself paramagnetic. Then the EPR method can be applied to study its properties directly.
Thus, in the case of a paramagnetic ligand, it is possible to study the interactions of “guest” molecules with the framework itself, and of a paramagnetic metal - the geometry of its local environment in the framework, as well as identify and measure distances to neighboring atoms. This approach is equally effective both for studying changes in the structure of MOFs under external influences and for assessing the efficiency of adsorption of industrially important gases (hydrogen, carbon dioxide, etc.).
Fighting resonance
But despite the sometimes disastrous consequences of the response effect, it is quite possible and necessary to fight it. To avoid the unwanted occurrence of this phenomenon, two methods of simultaneously applying resonance and combating it are usually used:
- “Dissociation” of frequencies is carried out, which, if they coincide, will lead to undesirable consequences. To do this, they increase the friction of various mechanisms or change the natural frequency of vibration of the system.
- They increase the damping of vibrations, for example, by placing the engine on a rubber lining or springs.