Sinusoid of effective and amplitude voltage
It is clear that this material is more aimed at a simple audience, who not only do not have an oscilloscope, but probably not everyone even has a multimeter. Therefore, all examples will be taken from the Electronics Workbench environment, which is accessible to everyone.
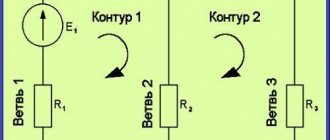
And the first thing we need to look at is the phase voltage sine wave from the outlet. To do this, we will draw a three-phase network in the program and connect the oscilloscope to one of the phases:
As can be seen with a voltmeter reading of 219.4 Volts between one of the phases and the PEN conductor, the oscilloscope showed a sine wave with an amplitude of 309.1 Volts. This voltage value is called maximum (amplitude). And 219.4 Volts, which the voltmeter shows, is the effective voltage. It is also called root mean square or effective. And before we move on to consider this feature, let’s briefly, in simple words, go through the drawn diagram of a three-phase network and understand the nature of the sinusoid.
Let's start with the diagram:
- From left to right - three AC voltage sources with phase angles of 0, 120, 240 degrees and connected by a star.
- The 4 Ohm resistor is the grounding of the transformer neutral.
- Resistors of 0.8 ohms are the conditional resistance of the wires, depending on the cross-section of the wire and the length of the line.
- Resistors 15, 10 and 20 Ohms - load of consumers in three phases.
- An oscilloscope is connected to one of the phases, showing an amplitude of 309.1 Volts.
Now let's look at a sinusoid. Alternating voltage, in contrast to constant voltage, the graph of which is straight on an oscilloscope, continuously changes both in magnitude and direction. Moreover, these changes occur periodically, that is, they are exactly repeated at regular intervals.
Alternating voltage is generated at power plants and reaches the end consumer through step-up and step-down distribution transformers. In this case, the transformation along the path does not affect the voltage sinusoid in any way.
Fundamentals of complex calculation of electrical circuits
Definition 1
Complex current is the complex effective value of a sinusoidal current.
One of the main ways to calculate AC electrical circuits is the symbolic or complex method. Typically, it is used in the analysis of electrical circuits with harmonic currents, voltages and electromotive force. As a result of the solution, a complex value of voltages and currents is obtained. A sinusoidal quantity can be represented:
- In the form of a rotating vector.
- As a complex number.
An example of a rotating vector is shown in the figure below.
Figure 1. An example of a rotating vector. Author24 - online exchange of student work
Are you an expert in this subject area? We invite you to become the author of the Directory Working Conditions
From this figure it can be seen that the sinusoidal value a changes over time, which can be the input voltage or any other parameter of the electrical network. The quantity has a certain initial value (t=0) at the initial phase φ:
Figure 2. Formula. Author24 - online exchange of student work
At angle Wt3, when the sum Wt3+ф=90 and accordingly:
Figure 3. Formula. Author24 - online exchange of student work
Finished works on a similar topic
Course work Integrated calculation of electrical networks 430 ₽ Abstract Integrated calculation of electrical networks 280 ₽ Test work Integrated calculation of electrical networks 190 ₽
Receive completed work or specialist advice on your educational project Find out the cost
The sinusoidal value at angle Wt7, when the sum Wt7 + f = 270 will have a negative value:
Figure 4. Formula. Author24 - online exchange of student work
The value will have a negative value at angles Wtn + φ = 0, when Wtn = –φ (this area is not marked in the figure), thus:
Figure 5. Formula. Author24 - online exchange of student work
Also, the sinusoidal value will have a zero value at angle Wt11, when Wt11+ ph = 360:
Figure 6. Formula. Author24 - online exchange of student work
It is according to this law that a sinusoidal quantity, for example voltage, can change, changing from 0 to the maximum value and back.
Another form of presentation is complex
Figure 7. Formula. Author24 - online exchange of student work
To do this, construct a graph (complex plane) of the dependence of two quantities, as in the figure below.
Figure 8. Graph. Author24 - online exchange of student work
The length of the vector Am is equal to the maximum value of the amplitude of the quantity under consideration. If we take into account the initial phase (φ), then this number is written as follows.
Figure 9. Formula. Author24 - online exchange of student work
In practical calculations of the complex method, it is not the amplitude value that is used, but the effective value, which is less than the root of 2 amplitude:
Figure 10. Formula. Author24 - online exchange of student work
When working with complex numbers, one of three ways to write a complex number is used: trigonometric form, algebraic form, exponential form. For example, there is a complex number in exponential form:
Figure 11. Formula. Author24 - online exchange of student work
In trigonometric form it will look like this:
Figure 12. Formula. Author24 - online exchange of student work
As a result, when moving to algebraic form, considering that:
Figure 13. Formula. Author24 - online exchange of student work
we get:
Figure 14. Formula. Author24 - online exchange of student work
where, ReA = 8.66 – real component of a complex number; ImA = 5 – imaginary component of a complex number.
When passing from the algebraic form to the exponential form, we obtain a number of the following form
Figure 15. Formula. Author24 - online exchange of student work
It goes to exponential form by the following transformation:
Figure 16. Formula. Author24 - online exchange of student work
And the angle is calculated by the formula
Figure 17. Formula. Author24 - online exchange of student work
And in the end it turns out:
Figure 18. Formula. Author24 - online exchange of student work