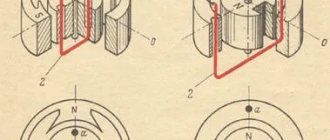
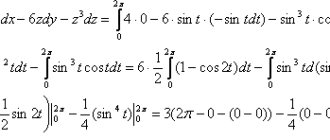Комплексные величины электрической цепи

Синусоида действующего и амплитудного напряжения

Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.

И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:

Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.

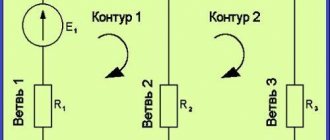
Начнем со схемы:

Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
Резистор 4 Ом — это заземление нейтрали трансформатора.
Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.

Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.

Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.

Основы комплексного расчета электрических цепей

Определение 1
Комплексный ток — это комплексное действующее значение синусоидального тока.

Одним из основных способов расчета электрических цепей переменного тока является символический или комплексный метод. Как правило, он используется при анализе электрических схем с гармоническими токами, напряжениями и электродвижущей силой. В результате решения получается комплексное значение напряжений и токов. Синусоидальная величина может быть представлена:

В форме вращающегося вектора.
В виде комплексного числа.

Пример вращающегося вектора изображен на рисунке ниже.

Рисунок 1. Пример вращающегося вектора. Автор24 — интернет-биржа студенческих работ

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы

По данному рисунку видно, что синусоидальная величина а изменяется с течением времени, которая может быть входным напряжением или любым другим параметром электрической сети. Величина имеет некоторое начальное значение (t=0) при начальной фазе ф:

Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ

При угле Wt3, когда сумма Wt3+ф=90 и соответственно:

Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Курсовая работа Комплексный расчет электрических сетей 430 ₽ Реферат Комплексный расчет электрических сетей 280 ₽ Контрольная работа Комплексный расчет электрических сетей 190 ₽

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

Синусоидальная величина при угле Wt7, когда сумма Wt7 + ф = 270 будет иметь отрицательное значение:

Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ

Величина будет иметь отрицательное значение при углах Wtn + ф = 0, когда Wtn = –ф (данная область на рисунке не отмечена), таким образом:

Рисунок 5. Формула. Автор24 — интернет-биржа студенческих работ

Также нулевое значение у синусоидальной величины будет при угле Wt11, когда Wt11+ ф = 360:

Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ

Именно по такому закону может меняться синусоидальная величина, например напряжение, изменяясь от 0 до максимального значения и обратно.

Другая форма представления — комплексная

Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ

Для этого строится график (комплексная плоскость) зависимости двух величин, как на рисунке ниже.

Рисунок 8. График. Автор24 — интернет-биржа студенческих работ

Длина вектора Аm равна максимальному значению амплитуды рассматриваемой величины. Если учитывать начальную фазу (ф), то это число записывается следующим образом.

Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ

В практических расчетах комплексного метода применяют не амплитудное значение, а действующее, которое меньше в корень из 2 амплитудного:

Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ

При работе с комплексными числами применяется один из трех способов записи комплексного числа: тригонометрическая форма, алгебраическая форма, показательная форма. Например, имеется комплексное число в показательной форме:

Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ

В тригонометрической форме оно будет иметь следующий вид:

Рисунок 12. Формула. Автор24 — интернет-биржа студенческих работ

В итоге при переходе в алгебраическую форму, учитывая, что:

Рисунок 13. Формула. Автор24 — интернет-биржа студенческих работ

получаем:

Рисунок 14. Формула. Автор24 — интернет-биржа студенческих работ

где, ReA = 8,66 – действительная составляющая комплексного числа; ImA = 5 – мнимая составляющая комплексного числа.

При переходе от алгебраической формы к показательной получаем число следующего вида

Рисунок 15. Формула. Автор24 — интернет-биржа студенческих работ

Оно переходит к показательной форме следующим преобразованием:

Рисунок 16. Формула. Автор24 — интернет-биржа студенческих работ