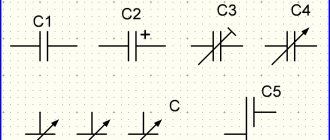Индуктивность контура — теоретические основы
Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.
По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током катушки L=Ψ/i.
Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Поток сцепления катушки индуктивности равен Ψ=L×i.
В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.
Напряжение на индуктивности уравновешивает ЭДС и может быть записано в виде uL=-eL=dΨ/dt=L×di/dt.
Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.
Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.
Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.
Конденсатор в цепи электрического тока
Принцип работы конденсатора простой – подается напряжение и накапливается заряд. Накопитель по-разному ведет себя в двух вариантах электрической цепи.
Постоянного
Если в цепь с присоединенным к ней конденсатором подать ток, то стрелка на амперметре придет в движение, после чего быстро вернется в предыдущее положение. Это связано с тем, что прибор быстро заряжается и ток исчез. Через обкладки разделенные диэлектриком постоянный ток проходить не может. Практическое применение конденсатора в такой цепи вызывает много вопросов. В условиях постоянного тока конденсатор функционирует, но непродолжительное время. Переходные процессы в виде зарядки и разрядки снимают все сомнения. В электронных схемах на постоянном токе конденсаторы один из самых распространенных компонентов.
Переменного
При подключении переменного напряжения полюса конденсатора меняют плюс на минус с частотой подачи напряжения. В данном случае электроны передвигаются сначала в одну, а потом в другую. На обкладках при такой смене остаются излишки заряда, которые собственно и создают ток во внешней цепи.
Конденсатор в цепи переменного тога выступает в качестве резистора.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока различается при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Вопросы и задачи
- Всегда ли одинаковы емкости двух одинаковых изолированных проводников?
- Можно ли зарядить лейденскую банку, не заземляя одну из обкладок?
- Какова примерно электрическая емкость вашего тела?
- Изменится ли емкость плоского конденсатора, если в воздушный зазор между его обкладками ввести незаряженную тонкую металлическую пластину?
- Найдите емкость системы конденсаторов, включенных между точками А
и
В
, как показано на рисунке. - Пластины заряженного плоского конденсатора попеременно заземляют. Что будет происходить с конденсатором при этом?
- Плоский конденсатор подключен к источнику постоянной ЭДС. Что нужно сделать, чтобы вокруг конденсатора возникло магнитное поле?
- В системе, изображенной на рисунке, соединяют с землей один раз внешнюю сферу, другой раз — внутреннюю. Будет ли одинакова емкость такого конденсатора в этих случаях?
- Почему, если параллельно рубильнику включить конденсатор, искрение при размыкании рубильника прекращается?
- Поверх длинного соленоида вплотную намотана катушка. Ток в соленоиде нарастает прямо пропорционально времени. Каков характер зависимости тока от времени в катушке?
- В городскую сеть включили катушку с большим числом витков. Измерив протекающий по катушке переменный ток, установили, что ее сопротивление равно 20 Ом. Затем поверх этой катушки намотали точно такую же вторую и включили ее в цепь параллельно первой. Будет ли общее сопротивление катушек составлять 10 Ом?
- Что произойдет, если трансформатор, рассчитанный на переменное напряжение первичной цепи 127 В, включить в сеть постоянного тока с напряжением 110 В?
- Разборный школьный трансформатор, ко вторичной обмотке которого подключена нагрузка, включен в сеть. Как изменится ток в первичной и вторичной катушках при удалении верхней части сердечника?
- Колебательный контур состоит из конденсатора постоянной емкости и катушки, в которую может вдвигаться сердечник. Один сердечник спрессован из порошка магнитного соединения железа (феррита) и является изолятором. Другой изготовлен из меди. Как изменится частота собственных колебаний контура, если в катушку вдвинуть а) медный сердечник, б) сердечник из феррита?
- В колебательном контуре изменили начальную величину заряда на конденсаторе. Какие характеристики возникающих в контуре электрических колебаний изменятся от этого, а какие — нет?
- Что произойдет, если заряженный конденсатор соединить сверхпроводником с таким же незаряженным конденсатором?
- Входящий в колебательный контур плоский конденсатор таков, что его пластины могут перемещаться одна относительно другой. Каким образом осуществить «раскачку» контура посредством перемещения пластин?
- Цепь переменного тока состоит из трех последовательно соединенных сопротивлений: омического, индуктивного и емкостного. Может ли одновременное увеличение каждого из них привести к уменьшению общего сопротивления?
- По цепи, изображенной на рисунке, передаются одновременно постоянный ток и ток высокой частоты. Что нужно сделать, чтобы в ветви А
проходил только постоянный ток, а в ветви
В
— только высокочастотный? - На рисунке показан участок цепи переменного тока. В каком случае напряжение U
не зависит от величины тока
I
?
Как найти индуктивность контура
Формула, которая является простейшей для нахождения величины, следующая:
- L = F : I,
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
- Ei = -L х dI : dt.
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
- W = L I2 : 2.
Ответы
- Нет, поскольку в присутствии других проводников их емкости могут изменяться.
- Нельзя, так как на изолированной обкладке вследствие индукции возникнут заряды обоих знаков, и банка не будет конденсатором.
- По порядку величины электрическая емкость тела человека такая же, как емкость шара диаметром 1 м. Она составляет примерно 50 пф.
- Не изменится.
- C
общ =
C
. Конденсатор емкостью
C
0 подсоединен к точкам, разность потенциалов между которыми равна нулю. - Каждая из пластин обладает определенной, обычно небольшой, емкостью относительно земли. При заземлении пластины нейтрализуется часть находящегося на ней заряда. Поэтому конденсатор будет разряжаться. Но разряжаться он будет тем медленнее, чем больше его емкость по сравнению с емкостью пластин относительно земли.
- В первом случае на большой сфере заряды будут располагаться только с внутренней стороны. Во втором случае они будут находиться с обеих сторон, и емкость всего конденсатора будет равна емкости системы двух параллельно соединенных конденсаторов с обкладками АВ
и
ВС
(см. рис.). - Нужно сближать или разводить пластины конденсатора.
- Ток самоиндукции, возникающий при размыкании цепи, заряжает конденсатор и не проходит в виде искры через рубильник.
- Бели катушка включена в замкнутую цепь, то в ней возникнет постоянный ток, время установления которого определяется индуктивностью катушки и ее сопротивлением.
- После того как на первую катушку намотали вторую, активное сопротивление стало вдвое меньше, а индуктивное осталось прежним. Следовательно, общее сопротивление уменьшится менее чем в два раза, т. е. будет больше 10 Ом.
- Обмотка трансформатора сгорит, так как у нее велико только индуктивное сопротивление, активное же — ничтожно мало.
- При удалении верхней части сердечника индуктивности первичной и вторичной катушек уменьшатся. Это приведет к уменьшению ЭДС самоиндукции в первичной обмотке и ЭДС индукции во вторичной. Следовательно, ток в первичной катушке увеличится, а во вторичной уменьшится.
- а) В медном сердечнике возникнут индукционные токи Фуко, магнитное поле которых будет ослаблять магнитное поле катушки. Это приведет к уменьшению ее индуктивности и, следовательно, к увеличению частоты колебаний, б) Сердечник из феррита увеличит магнитное поле катушки, соответственно возрастет индуктивность катушки, а частота — уменьшится.
- Изменятся амплитуды колебаний силы тока, напряжения, магнитной индукции; сохранится период колебаний.
- В системе возникнут незатухающие (если пренебречь излучением электромагнитных волн) колебания. При этом в момент, когда заряд распределен поровну между конденсаторами, энергия электростатического поля минимальна, а энергия магнитного поля максимальна.
- Когда заряд на пластинах конденсатора достигнет своего максимального значения, пластины следует раздвинуть, при этом совершенная работа пойдет на увеличение энергии контура. Когда заряд будет равен нулю, пластины следует сдвинуть до прежнего положения — энергия в контуре не изменится.
- Да, может.
- В ветвь А
нужно включить катушку индуктивности, а в ветвь
В
— конденсатор. - Если пренебречь активным сопротивлением, то \(~U = I \left( \omega L — \frac{1}{\omega C}\right)\). Напряжение не зависит от тока только тогда, когда \(~\omega L = \frac{1}{\omega C}\); в таком случае U
= 0 при любом
I
.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
- L= µ0n2V,
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
- L = µ0N2S : l,
Будет интересно➡ Определение направления вектора магнитной индукции
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Обозначение и единицы измерения
Сопротивление тока: формула
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.
Джозеф Генри
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
- В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
- В системе СГСЭ – в статгенри.
Свойства
Имеет следующие свойства:
- Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
- Не может быть отрицательной;
- Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
- При увеличении частоты тока реактивное сопротивление катушки увеличивается;
- Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
- Ce = C : (1 – 4Π2f2LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
- Lk = Lp + Lm + Lb,
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
Введение
Частотные характеристики конденсаторов являются важными параметрами, которые необходимы для разработки схем. Понимание частотных характеристик конденсатора позволит вам определить, например, какие шумы может подавлять конденсатор или какие флуктуации напряжения цепи питания он может контролировать. Эта статья описывает два типа частотных характеристик: |Z| (импеданс или полное сопротивление) и ESR (эквивалентное последовательное сопротивление конденсатора).
Импеданс Z идеального конденсатора определяется формулой 1, где ω — угловая частота, а C — емкость конденсатора.
Рисунок 1. Идеальный конденсатор
(1)
Из формулы 1 видно, что с увеличением частоты импеданс конденсатора уменьшается. Это показано на рисунке 1. В идеальном конденсаторе нет потерь и эквивалентное последовательное сопротивление (ESR) равно нулю.
Рисунок 2. Частотная характеристика идеального конденсатора
В реальном конденсаторе (рис. 3) существует некоторое сопротивление (ESR), вызванное диэлектрическими потерями, потерями на сопротивлении обкладок конденсатора и потерями связанные с сопротивлением утечки, а также паразитная индуктивность (ESL) выводов и обкладок конденсатора. В результате частотная характеристика импеданса принимает V образную форму (или U образную в зависимости от типа конденсатора), как показано на рисунке 4.Также на рисунке показана частотная характеристика ESR.
Рисунок 3. Реальный конденсатор
Рисунок 4. Пример частотной характеристики реального конденсатора
Причина, по которой графики |Z| и ESR имеют такой вид как на рисунке 4, можно объяснить следующим образом. Низкочастотная область |Z| в этой области уменьшается обратно пропорционально частоте, как и в идеальном конденсаторе. Значение ESR определяется диэлектрическими потерями в конденсаторе. Область резонанса При повышении частоты ESR, в результате паразитной индуктивности, сопротивления электродов и других факторов, вызывает отклонение |Z| от идеальной характеристики (красная пунктирная линия) и достигает минимального значения. Частота, на которой |Z| достигает минимума, называется собственной резонансной частотой и на этой частоте |Z| = ESR. После превышения собственной частоты резонанса, характеристика элемента меняется с емкостной на индуктивную и |Z| начинает повышаться. Область ниже собственной резонансной частоты называется емкостной областью, а область выше — индуктивной. В области резонанса к диэлектрическим потерям добавляются потери на электродах. Высокочастотная область При дальнейшем увеличении частоты характеристика |Z| определяется паразитной индуктивностью конденсатора. В высокочастотной области |Z| увеличивается пропорционально частоте, согласно формуле 2. Что касается ESR, в этой области начинают проявляться скин-эффект , эффект близости и другие.
(2)
Итак, мы рассмотрели частотную характеристику реального конденсатора. Здесь важно запомнить, что c повышением частоты ESR и ESL уже нельзя игнорировать. Поскольку существуют большое количество приложений, в которых конденсаторы используются на высоких частотах, ESR и ESL становятся важными параметрами, характеризующими конденсатор помимо значения его емкости.
Паразитные составляющие реальных конденсаторов имеют различное значение в зависимости от их типа. Давайте посмотрим на частотные характеристики разных конденсаторов. На рисунке 5 показаны графики |Z| и ESR для конденсаторов емкостью 10 мкФ. Все конденсаторы, кроме пленочных, планарные (SMD).
Рисунок 5. Частотные характеристики конденсаторов разных типов.
Для всех типов конденсаторов |Z| ведет себя одинаково до частоты 1 кГц. После 1 кГц импеданс увеличивается сильнее в алюминиевых и танталовых электролитических конденсаторах, чем в монолитных керамических и пленочных конденсаторах. Это происходит из-за того, что алюминиевые и танталовые конденсаторы имеют высокое удельное сопротивление электролита и большое ESR. В пленочных и монолитных керамических конденсаторах используются металлические материалы для электродов и, следовательно, они обладают очень маленьким ESR. Монолитные керамические конденсаторы и пленочные показывают примерно одинаковые характеристики до точки собственного резонанса, но у монолитных керамических конденсаторов резонансная частота выше, а |Z| в индуктивной области ниже. Эти результаты показывают, что импеданс монолитных керамических конденсаторов SMD типа в широком диапазоне частот имеет небольшое значение. Это делает их наиболее подходящими для высокочастотных приложений.
Существует также несколько типов монолитных керамических конденсаторов, изготовленных из различных материалов и имеющих различную форму. Давайте посмотрим, как эти факторы влияют на частотные характеристики. ESR ESR в емкостной области зависит от диэлектрических потерь, вызванных материалом диэлектрика. 2-й класс диэлектрических материалов на основе сегнетоэлектриков имеет высокую диэлектрическую постоянную и, как правило, высокое ESR. 1-ый класс материалов — температурно-компенсированные материалы на основе параэлектриков — имеют низкие диэлектрические потери и низкое ESR. На высоких частотах в области резонанса и индуктивной области, в дополнение к сопротивлению материала электродов, их форме и количеству слоев, ESR зависит от скин-эффекта и эффекта близости. Электроды часто делают из Ni, но для дешевых конденсаторов иногда применяют Cu, который тоже имеет низкое сопротивление. ESL ESL монолитных керамических конденсаторов сильно зависит от внутренней структуры электродов. Если размеры внутренних электродов задаются длиной, шириной и толщиной, то индуктивность ESL может быть определена математически. Значение ESL уменьшается, когда электроды конденсатора короче, шире и тоньше. На рисунке 6 показана связь между номинальной емкостью и резонансной частотой различных типов монолитных керамических конденсаторов. Вы можете видеть, что при уменьшении размеров конденсатора собственная резонансная частота увеличивается, а ESL уменьшается для одинаковых значений емкости. Это означает, что небольшие конденсаторы короткой длины лучше подходят для высокочастотных приложений.
Рисунок 6.
На рисунке 7 показан обратный LW конденсатор с короткой длиной L и большой шириной W. Из частотных характеристик, показанных на рисунке 8, можно увидеть, что LW конденсатор имеет меньший импеданс и лучшие характеристики, чем обычный конденсатор такой же емкости. С помощью LW конденсаторов можно достичь тех же характеристик, как у обычных конденсаторов, но меньшим числом компонентов. Уменьшение числа компонентов, позволяет сократить расходы и уменьшить монтажное пространство.
Рисунок 7. Внешний вид обратного LW конденсатора.
Рисунок 8. |Z| и ESR обратного LW конденсатора и конденсатора общего назначения
По материалам фирмы Murata. Вольный перевод
“Катушка ниток”
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
- I = U : R,
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь “катушка – источник тока”, то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от “витков в квадрате”.
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Будет интересно➡ Тепловое реле для электродвигателя
Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений
Общие сведения
Когда по цепи (рис. 6.5.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный токI,напряжение на конденсаторе UC отстает от тока I на 900, а напряжение на катушке индуктивности UL опережает ток на 900. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 1800).
Рис. 6.5.1
Когда одно из напряжений больше другого, цепь оказывается либо преимущественно индуктивной (рис. 6.5.2), либо преимущественно емкостной (рис. 6.5.3). Если напряжения UL иUС имеют одинаковые значения и компенсируют друг друга, то суммарное напряжение на участке цепи L – C оказывается равным нулю. Остается только небольшая составляющая напряжения на активном сопротивлении катушки и проводов. Такое явление называется резонансом напряжений (рис. 6.5.4).
| Рис. 6.5.2 | Рис. 6.5.3 | Рис. 6.5.4 |
При резонансе напряжений реактивное сопротивление цепи
X = XL – XC
оказывается равным нулю. При заданных значениях L и C резонанс может быть получен путем изменения частоты.
Поскольку XL = wL, а XC = 1 / wC, то резонансная частота w0 может быть определена из уравнения:
w0L –1/ w0C =0,
откуда
и .
Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения UL и UC могут существенно (в десятки раз!) превышать приложенное напряжение.
Экспериментальная часть
Задание
Для цепи с последовательным соединением конденсатора и катушки индуктивности измерьте действующие значения тока I и напряжений U, UC, ULпри w = w0, w0 и w>w0. Постройте векторные диаграммы.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 6.5.5), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2 В и частоту 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
Рис. 6.5.5
· Изменяя частоту приложенного напряжения, добейтесь резонанса по максимальному току. Для точной настройки по максимуму тока необходимо поддерживать неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входными напряжением и током. Тогда нет необходимости поддерживать входное напряжение неизменным.
· Произведите измерения и запишите в табл. 6.5.1 результаты измерений при резонансе f=f0приf1» 0,75f0иf2»1,25f0.
Таблица 6.5.1
| f, Гц | I, мА | U, B | UL, B | UC, B |
| f0 = | ||||
| f1 = | ||||
| f2 = |
· Постройте в одинаковом масштабе векторные диаграммы на рис. 6.5.6 для каждого из рассмотренных случаев.
Рис. 6.5.6
6.6. Параллельное соединение конденсатора и катушки индуктивности. Понятие о резонансе токов
Общие сведения
Когда к цепи (рис. 6.6.1) с параллельным соединением конденсатора и катушки индуктивности подается переменное синусоидальное напряжение U, одно и то же напряжение приложено к обоим элементам цепи.
Рис. 6.6.1
Общий ток цепи I разветвляется на ток в конденсаторе IC(емкостная составляющая общего тока) и ток в катушке IL (индуктивная составляющая общего тока), причем ток IL отстает от напряжения U на 900, а IC опережает на 900.
Токи IC и IL имеют противоположные фазы (1800) и в зависимости от их величин уравновешивают друг друга полностью или частично. Они могут быть представлены с помощью векторных диаграмм токов (рис. 6.6.2 — 4).
Когда IC = IL и общий ток цепи равен нулю, имеет место резонанс токов (векторная диаграмма рис. 6.6.2)
| Рис. 6.6.2 | Рис. 6.6.3 | Рис. 6.6.4 |
Когда IC > IL, т.е. преобладает ток конденсатора, общий ток цепи I являетсяпо характеру емкостными опережает напряжение U на 900 (рис. 6.6.3).
Когда IC< IL, т.е. преобладает ток катушки, общий ток цепи I является индуктивным и отстает от напряжения U на 900 (рис. 6.6.4).
Эти рассуждения проведены в пренебрежении потерями активной мощности в конденсаторе и катушке.
При резонансе токов реактивная проводимость цепи B = BL – BC равна нулю. Резонансная частота определяется из уравнения
,
откуда, так же, как и при резонансе напряжений,
и .
Полная проводимость при резонансе токов оказывается близкой к нулю. Остается нескомпенсированной лишь небольшая активная проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. Поэтому ток в неразветвленной части цепи имеет минимальное значение, тогда как токи IL и IC могут превышать его в десятки раз.
Экспериментальная часть
Задание
Для цепи с параллельным соединением конденсатора и катушки индуктивности измерьте действующие значения напряжения U и токов I, ICи ILпри w = w0, w0 и w>w0.Постройте векторные диаграммы.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 6.6.5), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 7 В, f = 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
Рис. 6.6.5
· Изменяя частоту приложенного напряжения, добейтесь резонанса по минимальному току I. Для точной настройки поддерживайте неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входным током и напряжением. Тогда необязательно поддерживать неизменным напряжение на входе цепи.
· Произведите измерения и запишите результаты измерений в табл. 6.6.1 при f = f0,f1»0,75f0иf2»1,25f0.
Таблица 6.6.1
| f, Гц | U, B | I, мА | IL, мА | IC, мА |
| f0 = | ||||
| f1 = | ||||
| f2 = |
· Постройте в одинаковом масштабе векторные диаграммы на рис. 6.6.6 для каждого из рассмотренных случаев.
Рис. 6.6.6
6.7. Частотные характеристики последовательного резонансного контура
Общие сведения
Частотными характеристиками обычно называют зависимости сопротивлений и проводимостей цепи от частоты синусоидального приложенного напряжения. Иногда к ним относят также зависимости от частоты токов, напряжений, фазовых сдвигов и мощностей.
В последовательном резонансном контуре (рис.6.7.1а) активное сопротивление не зависит от частоты, а индуктивное, ёмкостное и реактивное сопротивления изменяются в соответствии со следующими выражениями:
.
Рис. 6.7.1.
Полное сопротивление, как следует из треугольника сопротивлений (рис.6.7.1б):
Вид этих зависимостей от частоты представлен на рис.6.7.2а. При резонансной частоте w0=1/√(LC):
XL(w0)=XC(w0)= √(L/C)=r
Это сопротивление называется характеристическим сопротивлением резонансного контура, а отношение
r/R=Q
– добротностьюрезонансного контура
На рис.6.7.2б показаны графики изменения тока, напряжений на участках цепи и фазового сдвига при изменении частоты и неизменном приложенном напряжении в соответствии со следующими формулами:
I(w)=U/Z(w); UL(w)=wLI(w); UC=I/wC; φ=arctg[wL-1/(wCR)].
Если Q>1, то при резонансе напряжения UL(w0) и UC(w0) превышают приложенное напряжение в Q раз.
Рис. 6.7.2
При w0 цепь носит ёмкостный характер ( ток опережает напряжение на угол j), при w=w0 — активный, а при w>w0 — индуктивный (ток отстаёт от напряжения).
Экспериментальная часть
Задание
Снимите экспериментально частотные характеристики последовательного резонансного контура — R(w), X(w), Z(w), I(w), UL(w), UC(w) и j(w) — при Q>1.
Порядок выполнения работы
- Измерьте омметром активное сопротивление катушки индуктивности, указанной на схеме (рис.6.7.3).
.
R= Ом.
· Вычислите резонансную частоту, характеристическое сопротивление и добротность резонансного контура:
f0=1/2p√(LC)= Гц; r=√(L/C)= Ом; Q=r/R= .
- Соберите цепь согласно схеме (рис.6.7.3), включив в неё в качестве измерительных приборов соответствующие гнёзда коннектора и считая сопротивление R сопротивлением катушки индуктивности. Добавочное сопротивление Rдоб на этом этапе примите равным нулю (Q>1). Подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U=5 B, f=f0.
Рис. 6.7.3.
- Включите виртуальные приборы и по показанию фазометра настройте более точно резонансный режим, изменяя частоту приложенного напряжения. Сравните экспериментальную резонансную частоту с расчётной:
Экспериментальная f0= Гц.
Расчётная f0= Гц.
- Изменяя частоту от 0,2 до 2 кГц, запишите в табл.6.7.1 показания виртуальных приборов и по этим результатам на рис. 6.7.4. и 6.7.5. постройте графики частотных характеристик при добротности Q>1.
- Включите в цепь добавочное сопротивление Rдоб=100…330 Ом и убедитесь, что резонансная частота не изменилась, а ток и напряжения UL и UC при резонансе стали меньше.
Таблица 6.7.1.
| f, Гц | R, Ом | X, Ом | Z, Ом | I, мА | UC, В | URL, В | j, град |
6.8. Частотные характеристики параллельного резонансного контура
Общие сведения
В параллельном резонансном контуре (рис.6.8.1а) активная проводимость не зависит от частоты, а индуктивная, ёмкостная и реактивная проводимости изменяются в соответствии со следующими выражениями:
BL(w)=1/ωL; BC(w)=ωC; B(w)= BL(w)- BC(w);
Рис. 6.8.1.
Полная проводимость, как следует из треугольника проводимостей (рис.6.8.1б):
Y(w)=√(G2+B2).
Вид этих зависимостей от частоты представлен на рис.6.8.2а.
При резонансной частоте w0=1/√(LC):
BL(w0)=BC(w0)= √(C/L)=g .
Эта проводимость называется характеристической проводимостью резонансного контура, а отношение
g/G=Q
также как и в последовательном контуре– добротностью.
При изменении частоты и неизменном приложенном напряжении токи изменяются пропорционально соответствующим проводимостям:
I(w)=UY(w); IL(w)=U/wL; IC=UwC, ILC=UB(w).
При резонансной частоте w=w0 ток I, потребляемый от источника, имеет минимум и равен току в активном сопротивлении IR, а ток на реактивном участке цепи ILС равен нулю (см. рис. 6.8.2а). Реальные кривые могут несколько отличаться от рассмотренных идеальных, так как здесь не учитывалось активное сопротивление катушки.
Угол сдвига фаз (рис. 6.8.2.б) изменяется в соответствии с выражением:
φ=arctg[(1/wL-wC)/G].
При w0 цепь носит индуктивный характер (ток отстаёт от напряжения на угол j), при w=w0 — активный, а при w>w0 — ёмкостный (ток опережает напряжение). Если Q>1, то при резонансе токов IL(w0) и IC(w0) превышают ток источника I в Q раз.
Рис. 6.8.2
На рис. 6.8.2б кроме j(w) построены также зависимости от частоты полного Z(w) и реактивного X(w) сопротивлений. B общем случае (см.сплошные линии на рисунке):
Z(w)=1/Y(w)=1/√(G2+B2);
X(w)=B/(G2+B2).
При резонансе полное сопротивление принимает максимальное значение а реактивное обращается в ноль.
В идеализированном случае, когда активная проводимость настолько мала, что ей можно пренебречь (G=0):
X(w)=1/B; Z(w)=1/|B|.
Тогда в точке резонанса кривые X(w) и Z(w)имеют разрыв (см. пунктирные линии на рис.6.8.2б).
Экспериментальная часть
Задание
Снимите экспериментально частотные характеристики параллельного резонансного контура c высокой добротностью- I(w), IL(w), IC(w), X(w), Z(w)и j(w).
Порядок выполнения работы
- Соберите цепь согласно схеме (рис.6.8.3), включив в неё измерительные приборы или соответствующие гнёзда коннектора. В качестве катушки индуктивности с малым активным сопротивлением используйте обмотку трансформатора W=300 витков, вставив между подковами разъёмного сердечника полоски бумаги в один слой.
· Подайте на схему синусоидальное напряжение от генератора напряжений специальной формы U=5B, f=500Гц.
· Измерьте с помощью виртуальных приборов или рассчитайте по показаниям мультиметров реактивное сопротивление катушки индуктивности и рассчитайте индуктивность и резонансную частоту:
XL=U/IL= Ом;
L= XL/(2pf)= Гн;
f0=1/2p√(LC)= Гц.
Рис. 6.8.3.
- По показанию фазометра или по минимуму тока I настройте резонансный режим, изменяя частоту приложенного напряжения.. Сравните экспериментальную резонансную частоту с расчётной:
Экспериментальная f0= Гц.
Расчётная f0= Гц.
- Изменяя частоту от 0,2 до 1 кГц, запишите в табл.6.8.1 показания виртуальных приборов и по этим результатам на рис. 6.8.4. и 6.8.5. постройте графики частотных характеристик.
Примечания:
1. При отсутствии виртуальных приборов запишите в таблицу измеренные мультиметрами токи, а сопротивления рассчитайте по формулам, приведённым в разделе «Общие сведения». При этом фазовый сдвиг можно определить из векторных диаграмм, построенных для каждого значения частоты.
2. В области резонансной частоты экспериментальные точки должны быть расположены гуще, чем по краям графиков.
| f, Гц | X, Ом | Z, Ом | I, мА | IC, мА | IL, мА | j, град |
Таблица 6.7.1.
Общие сведения
Когда по цепи (рис. 6.5.1) с последовательным соединением конденсатора и катушки индуктивности протекает один и тот же синусоидальный токI,напряжение на конденсаторе UC отстает от тока I на 900, а напряжение на катушке индуктивности UL опережает ток на 900. Эти напряжения находятся в противофазе (повернуты относительно друг друга на 1800).
Рис. 6.5.1
Когда одно из напряжений больше другого, цепь оказывается либо преимущественно индуктивной (рис. 6.5.2), либо преимущественно емкостной (рис. 6.5.3). Если напряжения UL иUС имеют одинаковые значения и компенсируют друг друга, то суммарное напряжение на участке цепи L – C оказывается равным нулю. Остается только небольшая составляющая напряжения на активном сопротивлении катушки и проводов. Такое явление называется резонансом напряжений (рис. 6.5.4).
| Рис. 6.5.2 | Рис. 6.5.3 | Рис. 6.5.4 |
При резонансе напряжений реактивное сопротивление цепи
X = XL – XC
оказывается равным нулю. При заданных значениях L и C резонанс может быть получен путем изменения частоты.
Поскольку XL = wL, а XC = 1 / wC, то резонансная частота w0 может быть определена из уравнения:
w0L –1/ w0C =0,
откуда
и .
Полное сопротивление цепи при резонансе оказывается равным небольшому активному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжением и может оказаться довольно большим даже при маленьком приложенном напряжении. При этом напряжения UL и UC могут существенно (в десятки раз!) превышать приложенное напряжение.
Экспериментальная часть
Задание
Для цепи с последовательным соединением конденсатора и катушки индуктивности измерьте действующие значения тока I и напряжений U, UC, ULпри w = w0, w0 и w>w0. Постройте векторные диаграммы.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 6.5.5), подсоедините регулируемый источник синусоидального напряжения и установите напряжение на его входе 2 В и частоту 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
Рис. 6.5.5
· Изменяя частоту приложенного напряжения, добейтесь резонанса по максимальному току. Для точной настройки по максимуму тока необходимо поддерживать неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входными напряжением и током. Тогда нет необходимости поддерживать входное напряжение неизменным.
· Произведите измерения и запишите в табл. 6.5.1 результаты измерений при резонансе f=f0приf1» 0,75f0иf2»1,25f0.
Таблица 6.5.1
| f, Гц | I, мА | U, B | UL, B | UC, B |
| f0 = | ||||
| f1 = | ||||
| f2 = |
· Постройте в одинаковом масштабе векторные диаграммы на рис. 6.5.6 для каждого из рассмотренных случаев.
Рис. 6.5.6
6.6. Параллельное соединение конденсатора и катушки индуктивности. Понятие о резонансе токов
Общие сведения
Когда к цепи (рис. 6.6.1) с параллельным соединением конденсатора и катушки индуктивности подается переменное синусоидальное напряжение U, одно и то же напряжение приложено к обоим элементам цепи.
Рис. 6.6.1
Общий ток цепи I разветвляется на ток в конденсаторе IC(емкостная составляющая общего тока) и ток в катушке IL (индуктивная составляющая общего тока), причем ток IL отстает от напряжения U на 900, а IC опережает на 900.
Токи IC и IL имеют противоположные фазы (1800) и в зависимости от их величин уравновешивают друг друга полностью или частично. Они могут быть представлены с помощью векторных диаграмм токов (рис. 6.6.2 — 4).
Когда IC = IL и общий ток цепи равен нулю, имеет место резонанс токов (векторная диаграмма рис. 6.6.2)
| Рис. 6.6.2 | Рис. 6.6.3 | Рис. 6.6.4 |
Когда IC > IL, т.е. преобладает ток конденсатора, общий ток цепи I являетсяпо характеру емкостными опережает напряжение U на 900 (рис. 6.6.3).
Когда IC< IL, т.е. преобладает ток катушки, общий ток цепи I является индуктивным и отстает от напряжения U на 900 (рис. 6.6.4).
Эти рассуждения проведены в пренебрежении потерями активной мощности в конденсаторе и катушке.
При резонансе токов реактивная проводимость цепи B = BL – BC равна нулю. Резонансная частота определяется из уравнения
,
откуда, так же, как и при резонансе напряжений,
и .
Полная проводимость при резонансе токов оказывается близкой к нулю. Остается нескомпенсированной лишь небольшая активная проводимость, обусловленная активным сопротивлением катушки и несовершенной изоляцией конденсатора. Поэтому ток в неразветвленной части цепи имеет минимальное значение, тогда как токи IL и IC могут превышать его в десятки раз.
Экспериментальная часть
Задание
Для цепи с параллельным соединением конденсатора и катушки индуктивности измерьте действующие значения напряжения U и токов I, ICи ILпри w = w0, w0 и w>w0.Постройте векторные диаграммы.
Порядок выполнения работы
· Соберите цепь согласно схеме (рис. 6.6.5), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U = 7 В, f = 500 Гц. В качестве индуктивности с малым активным сопротивлением используйте катушку трансформатора 300 витков, вставив между подковами разъемного сердечника полоски бумаги в один слой (немагнитный зазор).
Рис. 6.6.5
· Изменяя частоту приложенного напряжения, добейтесь резонанса по минимальному току I. Для точной настройки поддерживайте неизменным напряжение на входе цепи. При измерениях виртуальными приборами резонанс настраивается по переходу через ноль угла сдвига фаз между входным током и напряжением. Тогда необязательно поддерживать неизменным напряжение на входе цепи.
· Произведите измерения и запишите результаты измерений в табл. 6.6.1 при f = f0,f1»0,75f0иf2»1,25f0.
Таблица 6.6.1
| f, Гц | U, B | I, мА | IL, мА | IC, мА |
| f0 = | ||||
| f1 = | ||||
| f2 = |
· Постройте в одинаковом масштабе векторные диаграммы на рис. 6.6.6 для каждого из рассмотренных случаев.
Рис. 6.6.6
6.7. Частотные характеристики последовательного резонансного контура
Общие сведения
Частотными характеристиками обычно называют зависимости сопротивлений и проводимостей цепи от частоты синусоидального приложенного напряжения. Иногда к ним относят также зависимости от частоты токов, напряжений, фазовых сдвигов и мощностей.
В последовательном резонансном контуре (рис.6.7.1а) активное сопротивление не зависит от частоты, а индуктивное, ёмкостное и реактивное сопротивления изменяются в соответствии со следующими выражениями:
.
Рис. 6.7.1.
Полное сопротивление, как следует из треугольника сопротивлений (рис.6.7.1б):
Вид этих зависимостей от частоты представлен на рис.6.7.2а. При резонансной частоте w0=1/√(LC):
XL(w0)=XC(w0)= √(L/C)=r
Это сопротивление называется характеристическим сопротивлением резонансного контура, а отношение
r/R=Q
– добротностьюрезонансного контура
На рис.6.7.2б показаны графики изменения тока, напряжений на участках цепи и фазового сдвига при изменении частоты и неизменном приложенном напряжении в соответствии со следующими формулами:
I(w)=U/Z(w); UL(w)=wLI(w); UC=I/wC; φ=arctg[wL-1/(wCR)].
Если Q>1, то при резонансе напряжения UL(w0) и UC(w0) превышают приложенное напряжение в Q раз.
Рис. 6.7.2
При w0 цепь носит ёмкостный характер ( ток опережает напряжение на угол j), при w=w0 — активный, а при w>w0 — индуктивный (ток отстаёт от напряжения).
Экспериментальная часть
Задание
Снимите экспериментально частотные характеристики последовательного резонансного контура — R(w), X(w), Z(w), I(w), UL(w), UC(w) и j(w) — при Q>1.
Порядок выполнения работы
- Измерьте омметром активное сопротивление катушки индуктивности, указанной на схеме (рис.6.7.3).
.
R= Ом.
· Вычислите резонансную частоту, характеристическое сопротивление и добротность резонансного контура:
f0=1/2p√(LC)= Гц; r=√(L/C)= Ом; Q=r/R= .
- Соберите цепь согласно схеме (рис.6.7.3), включив в неё в качестве измерительных приборов соответствующие гнёзда коннектора и считая сопротивление R сопротивлением катушки индуктивности. Добавочное сопротивление Rдоб на этом этапе примите равным нулю (Q>1). Подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U=5 B, f=f0.
Рис. 6.7.3.
- Включите виртуальные приборы и по показанию фазометра настройте более точно резонансный режим, изменяя частоту приложенного напряжения. Сравните экспериментальную резонансную частоту с расчётной:
Экспериментальная f0= Гц.
Расчётная f0= Гц.
- Изменяя частоту от 0,2 до 2 кГц, запишите в табл.6.7.1 показания виртуальных приборов и по этим результатам на рис. 6.7.4. и 6.7.5. постройте графики частотных характеристик при добротности Q>1.
- Включите в цепь добавочное сопротивление Rдоб=100…330 Ом и убедитесь, что резонансная частота не изменилась, а ток и напряжения UL и UC при резонансе стали меньше.
Таблица 6.7.1.
| f, Гц | R, Ом | X, Ом | Z, Ом | I, мА | UC, В | URL, В | j, град |
6.8. Частотные характеристики параллельного резонансного контура
Общие сведения
В параллельном резонансном контуре (рис.6.8.1а) активная проводимость не зависит от частоты, а индуктивная, ёмкостная и реактивная проводимости изменяются в соответствии со следующими выражениями:
BL(w)=1/ωL; BC(w)=ωC; B(w)= BL(w)- BC(w);
Рис. 6.8.1.
Полная проводимость, как следует из треугольника проводимостей (рис.6.8.1б):
Y(w)=√(G2+B2).
Вид этих зависимостей от частоты представлен на рис.6.8.2а.
При резонансной частоте w0=1/√(LC):
BL(w0)=BC(w0)= √(C/L)=g .
Эта проводимость называется характеристической проводимостью резонансного контура, а отношение
g/G=Q
также как и в последовательном контуре– добротностью.
При изменении частоты и неизменном приложенном напряжении токи изменяются пропорционально соответствующим проводимостям:
I(w)=UY(w); IL(w)=U/wL; IC=UwC, ILC=UB(w).
При резонансной частоте w=w0 ток I, потребляемый от источника, имеет минимум и равен току в активном сопротивлении IR, а ток на реактивном участке цепи ILС равен нулю (см. рис. 6.8.2а). Реальные кривые могут несколько отличаться от рассмотренных идеальных, так как здесь не учитывалось активное сопротивление катушки.
Угол сдвига фаз (рис. 6.8.2.б) изменяется в соответствии с выражением:
φ=arctg[(1/wL-wC)/G].
При w0 цепь носит индуктивный характер (ток отстаёт от напряжения на угол j), при w=w0 — активный, а при w>w0 — ёмкостный (ток опережает напряжение). Если Q>1, то при резонансе токов IL(w0) и IC(w0) превышают ток источника I в Q раз.
Рис. 6.8.2
На рис. 6.8.2б кроме j(w) построены также зависимости от частоты полного Z(w) и реактивного X(w) сопротивлений. B общем случае (см.сплошные линии на рисунке):
Z(w)=1/Y(w)=1/√(G2+B2);
X(w)=B/(G2+B2).
При резонансе полное сопротивление принимает максимальное значение а реактивное обращается в ноль.
В идеализированном случае, когда активная проводимость настолько мала, что ей можно пренебречь (G=0):
X(w)=1/B; Z(w)=1/|B|.
Тогда в точке резонанса кривые X(w) и Z(w)имеют разрыв (см. пунктирные линии на рис.6.8.2б).
Экспериментальная часть
Задание
Снимите экспериментально частотные характеристики параллельного резонансного контура c высокой добротностью- I(w), IL(w), IC(w), X(w), Z(w)и j(w).
Порядок выполнения работы
- Соберите цепь согласно схеме (рис.6.8.3), включив в неё измерительные приборы или соответствующие гнёзда коннектора. В качестве катушки индуктивности с малым активным сопротивлением используйте обмотку трансформатора W=300 витков, вставив между подковами разъёмного сердечника полоски бумаги в один слой.
· Подайте на схему синусоидальное напряжение от генератора напряжений специальной формы U=5B, f=500Гц.
· Измерьте с помощью виртуальных приборов или рассчитайте по показаниям мультиметров реактивное сопротивление катушки индуктивности и рассчитайте индуктивность и резонансную частоту:
XL=U/IL= Ом;
L= XL/(2pf)= Гн;
f0=1/2p√(LC)= Гц.
Рис. 6.8.3.
- По показанию фазометра или по минимуму тока I настройте резонансный режим, изменяя частоту приложенного напряжения.. Сравните экспериментальную резонансную частоту с расчётной:
Экспериментальная f0= Гц.
Расчётная f0= Гц.
- Изменяя частоту от 0,2 до 1 кГц, запишите в табл.6.8.1 показания виртуальных приборов и по этим результатам на рис. 6.8.4. и 6.8.5. постройте графики частотных характеристик.
Примечания:
1. При отсутствии виртуальных приборов запишите в таблицу измеренные мультиметрами токи, а сопротивления рассчитайте по формулам, приведённым в разделе «Общие сведения». При этом фазовый сдвиг можно определить из векторных диаграмм, построенных для каждого значения частоты.
2. В области резонансной частоты экспериментальные точки должны быть расположены гуще, чем по краям графиков.
| f, Гц | X, Ом | Z, Ом | I, мА | IC, мА | IL, мА | j, град |
Таблица 6.7.1.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Керамические конденсаторы
Типы и свойства керамик
Данный тип конденсаторов относится к конденсаторам с неорганическим диэлектриком. Керамические конденсаторы — это самый массовый вид конденсаторов, что обусловлено их высокими и стабильными характеристиками, простотой производства, пригодностью для автоматизированного монтажа [1]. Керамические конденсаторы получили свое название потому, что в качестве диэлектрика в них применяется радиочастотная керамика на основе титана, циркония и оксидов других материалов. Чаще всего радиочастотная керамика производится из диоксида титана (TiO2), титаната бария (BaTiO3) или титаната стронция (SrTiO3), хотя точные формулы керамики у разных производителей различаются.
Теперь необходимо сказать несколько слов о классификации керамических конденсаторов. Достаточно часто «сверхцелью» обзорной статьи по электронным компонентам становится попытка дать разработчику универсальный инструмент по выбору компонентов для использования в конкретном применении, основанный на классификации по различным параметрам. Применительно к керамическим конденсаторам попытки создать классификацию «в помощь разработчику» надо признать скорее неудачными. У этого есть не одна причина, и в «сухом остатке» правильнее будет признать, что самый надежный способ выбора керамических конденсаторов для конкретного применения — читать даташит.
Достаточно упомянуть, что свои версии классификации предложены двумя инженерными сообществами: IEC (International Electrotechnical Commissiom) и EIA (Electronic Industries Alliance). Классификации имеют различия. Так, EIA разделяет керамику на четыре класса, а IEC — на три. Тот факт, что значительная часть производителей (в основном американских) использует в маркировке своих изделий классификацию EIA, а другая — IEC, лишь усложняет задачу по выбору компонентов. Сюда нужно добавить, что кодировку IEC также называют Industrial, хотя по смыслу обе кодировки работают в индустриальном диапазоне температур. Имеется и отдельная Military-кодировка. В этом разделе статьи будут упоминаться в основном кодировки EIA и Industrial.
Были попытки классификации, основанные на разделении конденсаторов по применению, в которых, тем не менее, можно увидеть, что разделение по применению преимущественно связано с частотой. Та же EIA предлагает делить керамические конденсаторы на два больших класса. Можно достаточно условно выделить более высокочастотные применения (резонансные контуры и т. п. аппаратуры), где немалое значение имеют малые потери и высокая стабильность емкости, и менее высокочастотные применения (цепи фильтрации и прочее), где эти параметры не столь значимы ([1], EIA).
Керамические конденсаторы относятся к конденсаторам с нормируемым значением ТКЕ. Как уже упоминалось, Ассоциация производителей электронного оборудования (EIA) разделяет керамику на четыре класса и типы внутри каждого класса. Чем меньше номер класса, тем выше общие характеристики конденсатора, но больше размер для данной емкости. Типы в пределах каждого класса определяют рекомендуемый диапазон рабочих температур и ТКЕ, включая температурный дрейф и допуск в указанном температурном дрейфе. EIA определяет основные параметры конденсаторов для каждого класса и методы их измерения. Это касается сопротивления изоляции, тангенса угла диэлектрических потерь, диэлектрической абсорбции и других основных параметров конденсаторов.
Разделение керамических конденсаторов на классы в достаточной степени условное, поскольку не указано жестких требований на каждый класс. Например, конденсаторами 1‑го класса принято считать «точные конденсаторы с температурной компенсацией, с высокой стабильностью по напряжению, температуре и частоте». Конденсаторы 1‑го класса характеризуются температурным коэффициентом не хуже ±3% на градус при +25…+85 °C. Для конденсаторов 1‑го класса может быть достигнута точность в 1%, хотя наиболее типичной считается точность 5–10%. Температурная зависимость емкости для конденсаторов 1‑го класса считается линейной. Разделение керамических конденсаторов на классы производится по типу керамики, которая использована при их изготовлении. Для обозначения типов керамики EIA ввела набор кодов. Коды керамических конденсаторов 1‑ и 2‑го классов различаются. Кроме того, существует два варианта обозначения типа керамики — в соответствии со стандартом EIA-RS‑198 и упомянутым выше промышленным стандартом Industrial. В таблице 1 представлена расшифровка кодировки EIA для керамики 1‑го класса.
Таблица 1.Кодировка EIA-RS‑198 керамики по наклону температурной кривой (класс 1)
| Температурный коэффициент (наклон температурной кривой) | Множитель температурного коэффициента | Допустимое отклонение температурного коэффициента, +25… +85 °C | |||
| Буква | Ppm/°С | Цифра | Множитель | Буква | Ppm/°С |
| C | 0 | 0 | –1 | G | ±30 |
| B | 0,3 | 1 | –10 | H | ±60 |
| L | 0,8 | 2 | –100 | J | ±120 |
| A | 0,9 | 3 | –1000 | K | ±250 |
| M | 1 | 4 | +1 | L | ±500 |
| P | 1,5 | 6 | +10 | M | ±1000 |
| R | 2,2 | 7 | +100 | N | ±2500 |
| S | 3,3 | 8 | +1000 | ||
| T | 4,7 | ||||
| V | 5,6 | ||||
| U | 7,5 | ||||
Например, наиболее часто в конденсаторах 1‑го класса применяется керамика C0G. Это означает, что в температурном диапазоне +25…+85 °C наклон температурной кривой будет нулевым (0), то есть зависимости емкости от температуры не будет. Это можно увидеть на рис. 1, 2, где конденсаторы C0G обозначены как NP0 (обозначение, используемое в стандарте Industrial). Множитель температурного коэффициента вместе с самим коэффициентом также определяет наклон температурной кривой и соответственно степень изменения емкости от вариации температуры. В нашем примере (C0G) коэффициент 1 не изменит наклон температурной кривой, заданный основным температурным коэффициентом (0), который в англоязычной литературе часто называется Significant Figures. Знак перед множителем температурного коэффициента определяет направление изменения емкости: знак «–» говорит о том, что с повышением температуры емкость будет уменьшаться. Действие знака при множителе температурного коэффициента наглядно демонстрируется на рис. 1. К рисунку необходимо сделать пояснение. Промышленное обозначение керамики, основанное на Negativ/Positiv-обозначениях, считается более устаревшим по отношению к обозначениям EIA, но при этом более интуитивно понятным и состоит из буквы (N — для обозначения отрицательного температурного коэффициента, P — для обозначения положительного температурного коэффициента) и числа, указывающего температурную погрешность. Сравнение кодировки по EIA и промышленной кодировки видно из таблицы 2.
Таблица 2.Сравнительная кодировка EIA и Industrial
| Industry | P100 | NP0 | N030 | N075 | N150 | N220 | N330 | N470 | N750 | N1500 | N2200 |
| EIA | M7G | C0G | B2G | U1G | P2G | R2G | S2H | T2H | U2J | P3K |
Теперь, собственно, рис. 1, о котором упоминалось выше. На нем представлено изменение емкости от температуры для керамики 1‑го класса. Различные керамические материалы на этом рисунке имеют кодировку Industrial (выделено цветом), и по таблице 2 можно найти соответствие им в кодировке EIA (черные обозначения в рамках). При сравнении таблиц 1 и 2 видно действие знака множителя температурного коэффициента, проиллюстрированное на рис. 1.
Рис. 1. Идеализированные кривые зависимости емкости от температуры керамики 1 го класса
Основное отличие керамики 2‑го класса от 1‑го — нелинейная зависимость емкости от температуры. Это хорошо видно на рис. 2, где сравнивается керамика 1‑го класса C0G (NP0) с двумя образцами 2‑го класса (X7R, Y5V). В общем и целом конденсаторы 2‑го класса обладают большей объемной эффективностью, что связано с высокой диэлектрической проницаемостью керамики 2‑го класса и напрямую отражается на размерах конденсаторов.
Рис. 2. Сравнение температурных характеристик керамики 1 го и 2 го классов
Температурная кодировка EIA конденсаторов 2‑го класса приведена в таблице 3.
Таблица 3.Кодировка EIA-RS‑198 керамики без температурной компенсации (класс 2 и выше)
| Наименьшая рабочая температура | Наибольшая рабочая температура | Изменение емкости | |||
| Буква | Температура, °С | Цифра | Температура, °С | Буква | в % |
| X | –55 | 4 | +65 | A | ±1 |
| Y | –30 | 5 | +85 | B | ±1,5 |
| Z | +10 | 6 | +105 | C | ±2,2 |
| 7 | +125 | D | ±3,3 | ||
| 8 | +150 | E | ±4,7 | ||
| 9 | +200 | F | ±7,5 | ||
| P | ±10 | ||||
| R | ±15 | ||||
| S | ±22 | ||||
| T | +22/–33 | ||||
| U | +22/–56 | ||||
| V | +22/–82 | ||||
Кроме описанной выше зависимости от температуры, керамика 2‑го класса также имеет явную зависимость емкости от приложенного постоянного или медленно меняющегося напряжения. Суть этого явления заключается в том, что при приложении постоянного напряжения к сегнетоэлектрикам, используемым в качестве керамики в конденсаторах 2‑го класса, происходит снижение диэлектрической проницаемости из-за эффектов поляризации. Как следствие, уменьшается и связанная с диэлектрической проницаемостью емкость. В англоязычной документации это явление часто описывается термином DC-bias (смещение по постоянному току).
Это свойство практически никогда не упоминается при попытках классификации конденсаторов, и конкретные значения изменения емкости могут быть получены в основном при изучении технической документации на конкретное изделие.
Также необходимо отметить, что значительный вклад в описание данного явления внесен сотрудниками японской фирмы Murata. Ими были проведены исследования доменных структур керамики и предложены интерактивные программные средства для инженеров — разработчиков аппаратуры, позволяющие учесть DC-bias при проектировании. На рис. 3 можно увидеть пример от Murata — здесь представлена зависимость емкости от постоянного напряжения для керамических конденсаторов 2‑го класса (X5R, X7R).
Рис. 3. Пример зависимости емкости керамики X5R, X7R от приложенного постоянного напряжения (Murata)
Прямое соответствие между типом керамики и частотным диапазоном указывается в технической документации на тот или иной конденсатор. Считается, что конденсаторы 1‑го класса являются более высокочастотными и имеют в верхнем высокочастотном диапазоне наименьшие потери и наименьшее рассеяние. Тем не менее конденсаторы 1‑го класса имеют прямую зависимость максимальной рабочей частоты от номинала конденсатора. Это можно увидеть в таблице 4 при сравнении двух видов керамики в частотной области.
Таблица 4.Сравнение керамики 1‑го и 2‑го классов
| 10 пФ | 100 пФ | 1 нФ | 10 нФ | 100 нФ | 1 мкФ |
| C0G (класс 1) | 1550 MГц | 460 MГц | 160 MГц | 55 MГц | |
| X7R (класс 2) | 190 MГц | 56 MГц | 22 MГц | 10 MГц |
И следует иметь в виду, что диэлектрики 2-го, 3‑го и 4‑го классов являются пьезоэлектриками, а потому конденсаторы данных классов подвержены микрофонному эффекту. Это обязательно необходимо учитывать при решении о применении конденсаторов указанных классов на частотах выше 200 МГц. Но при использовании подобных конденсаторов в источниках питания, даже импульсных, микрофонный эффект проявляется не так явно, за исключением случаев, когда рабочая частота находится в звуковом диапазоне. Влияние пьезоэффекта на керамику 2‑го класса меньше, чем на керамику 3‑го и 4‑го классов. Наличие пьезоэффекта у большинства типов керамики, применяемой при производстве керамических конденсаторов, требует при проектировании электрических цепей с керамическими конденсаторами обязательного учета реактивной мощности, рассеиваемой на конденсаторах, поскольку в условиях, когда реактивная мощность равна или превышает активную мощность, рассеиваемую на конденсаторах, происходит быстрое старение керамики с последующим ее разрушением. Это особенно важно, когда керамические конденсаторы используются в силовых или фильтрующих цепях, например в цепях питания процессоров компьютеров.
Кроме классификации по типу керамики, керамические конденсаторы ранжируются по конструктивному исполнению. Различают следующие группы керамических конденсаторов:
- дисковые конденсаторы с полимерным покрытием для печатного монтажа (disk);
- однослойные керамические конденсаторы (single layer);
- многослойные прямоугольные конденсаторы для поверхностного монтажа (multilayer);
- бескорпусные дисковые конденсаторы для поверхностного монтажа для использования в УВЧ-диапазоне (дециметровый диапазон волн);
- трубчатые конденсаторы для печатного монтажа, в настоящее время применяются крайне редко.
Однослойные (монолитные) керамические конденсаторы (Single Layer Ceramic Capacitor, SLCC)
В классе керамических конденсаторов следует отметить тип так называемых однослойных, или монолитных, конденсаторов.
Поскольку для производства SLCC используются те же керамики, те же проводящие материалы и во многом схожие технологии, что и для производства многослойных конденсаторов, имеется значительное сходство свойств MLCC и SLCC по отношению к температуре и частоте.
Однослойные керамические конденсаторы представляют собой в некотором роде элементарный классический конденсатор, поскольку их конструкция состоит из двух электродов, между которыми расположен слой высокочастотной керамики (рис. 4).
Рис. 4. Конструкция однослойного конденсатора компании Dielectric Laboratories
Конденсаторы этого типа производятся по технологии спекания разнородных материалов и представляют собой, по сути, композитный сплав керамика-металл. Поэтому они предназначены в первую очередь для применения в интегральных сборках, в том числе сверхвысокочастотных. Хотя некоторые производители, например компания Vishay, по этой же технологии выпускают дисковые конденсаторы (Disk) для печатного монтажа. К несомненным преимуществам однослойных монолитных конденсаторов относятся:
- очень низкие потери на прохождение и малое рассеяние на частотах до 50 ГГц;
- диапазон рабочих частот: до 100 ГГц;
- надежная и прочная конструкция, в том числе на излом;
- номинальная емкость: 0,04–6200 пФ;
- диэлектрическая постоянная керамики: 14–25000;
- рабочее напряжение: до 100 В.
Классификация однослойных конденсаторов
Существует несколько вариантов классификации однослойных конденсаторов. Один из них использует компания Dielectric Laboratories. Он включает следующие типы:
- Border Cap — обычные плоские широкополосные конденсаторы с уменьшенной на одной или двух сторонах металлизацией. Уменьшение площади металлизации помогает предотвратить замыкание обкладок при монтаже и улучшает визуальный контроль Внешний вид и типы таких конденсаторов представлены на рис. 4.
- Di-Cap — обычные плоские широкополосные конденсаторы, площадь металлизации которых равна площади керамики. Используются в диапазоне частот 100 кГц – 80 ГГц. Этого же типа конденсаторы могут быть выводными (рис. 5).
- Gap Cap — два последовательно соединенных конденсатора на одной керамической пластине (рис. 6). Конденсаторы этого типа могут последовательно включаться в микрополосковую линию без использования проводников.
- Bar Cap1— конденсаторные сборки. Основной диапазон применений до 30 ГГц. Производятся для использования, в том числе, в монолитных сверхвысокочастотных микросхемах (monolithic microwave integrated circuit — MMIC), рис. 7.
- Bi-Cap (Binary-Cap) — несколько конденсаторов на одной керамической пластине. Емкости соотносятся как степени двойки. Основной диапазон применений до 30 ГГц. Используются при прототипировании и тонкой настройке схем. Имеют размеры, сравнимые с геометрией компонентов, используемых в СВЧ-устройствах. Конденсаторы на одной пластине могут применяться как одиночно, так и в комбинации (рис. 8).
- T‑Cap — серия конденсаторов, аналогичная Di-Cap. Имеет другой размерный ряд.
- Milli-Cap — конденсаторы для поверхностного монтажа.
Рис. 5. Выводные конденсаторы Di-Cap от Dielectric Laboratories
Рис. 6. Gap-Cap от Dielectric Laboratories
Рис. 7. Bar-Cap от Dielectric Laboratories
Рис. 8. Bi-Cap от Dielectric Laboratories
Представляет интерес сравнительная частотная характеристика нескольких типов однослойных конденсаторов, представленная на рис. 9. Далее подобная диаграмма будет представлена для многослойных конденсаторов.
Рис. 9. Сравнительная частотная характеристика разных типов однослойных конденсаторов
Применение SLCC
В силу обусловленных конструкцией классического однослойного конденсатора небольших значений емкости и выдающихся частотных свойств керамик, SLCC получили максимальное распространение в высокочастотных и сверхвысокочастотных приложениях. Применение видов керамики с большими значениями диэлектрической постоянной позволяет поддерживать тренд на перманентную миниатюризацию данного класса конденсаторов. Наглядную иллюстрацию этому можно найти в материалах компании AVX [2] (рис. 10).
Рис. 10. Миниатюризация SLCC [1]
Типичным примером свойств, удовлетворяющих современным требованиям к СВЧ-комплектующим, можно считать серию сверхширокополосных блокирующих однослойных керамических конденсаторов GX от AVX [2]. Изделия характеризуются сверхмалыми вносимыми потерями и малыми обратными потерями. Используются в диапазоне частот до 40 ГГц и напряжений до 50 В, имеют емкости до 100 нФ и форм-фактор 0603-0201. На рис. 11 представлен типичный график вносимых потерь для серии GX0S.
Рис. 11. Вносимые потери (S21) для серии блокирующих конденсаторов GX0S (AVX)
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).
Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Реальные параметры конденсатора
Думаю, все вы в курсе, что в нашем бесшабашном мире нет ничего идеального. То же самое касается и электроники. Радиоэлементы, каскады, радиоузлы также частенько дают сбои. Можно даже вспомнить недавнюю историю с космическим кораблем «Прогресс». Сбой какого-то узла повлек гибель целого гиганта космической отрасли. Даже простой, на первый взгляд, радиоэлемент конденсатор, имеет в своем составе не только емкость, но и другие паразитные параметры. Давайте рассмотрим схему, из чего все-таки состоит наш реальный конденсатор?
где
r — это сопротивление диэлектрика и корпуса между обкладками конденсатора
С — собственно сама емкость конденсатора
ESR — эквивалентное последовательное сопротивление
ESI (чаще его называют ESL) — эквивалентная последовательная индуктивность
Вот на самом деле из чего состоит простой безобидный конденсатор, особенно электролитический. Рассмотрим эти параметры более подробно:
r — сопротивление диэлектрика. Диэлектриком может быть электролит в электролитических конденсаторах, бумага или еще какая-нибудь дрянь). Также между выводами конденсатора находится его корпус. Он тоже обладает каким-то сопротивлением и тоже сделан из диэлектрика и относится сюда же.
С — емкость конденсатора, которая написана на самом конденсаторе плюс-минус некоторые отклонения, связанные с погрешностью.
ESI(ESL) — последовательная индуктивность — это собственная индуктивность обкладок и выводов. На низких частотах можно не учитывать. Почему? Читаем статью катушка индуктивности в цепи постоянного и переменного тока.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
- µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
- N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.
Будет интересно➡ Особенности применения проходных выключателей
Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
- l — длина проводника в метрах;
- r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Почему вредно большое значение ESR
Раньше, еще когда только-только стали появляться первые электронные схемы, такой параметр, как ESR даже ни у кого не был на слуху. Может быть и знали, что есть это сопротивление, но оно никому не вредило. Но… с появлением первых импульсных блоков питания все чаще стали говорить о ESR. Чем же столь безобидное сопротивление не понравилось импульсным блокам питания?
На нулевой частоте (постоянный ток) и низких частотах, как вы помните из статьи конденсатор в цепи постоянного и переменного тока, конденсатор сам оказывает большое сопротивление электрическому току. В этом случае какие-то паразитные доли Ома сопротивления ESR не будут влиять на параметры электрической цепи. Все самое интересное начинается тогда, когда конденсатор работает в высокочастотных цепях (ВЧ).
Мы с вами знаем, что конденсатор пропускает через себя переменный ток. И чем больше частота, тем меньше сопротивление самого конденсатора. Вот вам формула, если позабыли:
где, ХС — это сопротивление конденсатора, Ом
П — постоянная и равняется приблизительно 3,14
F — частота, измеряется в Герцах
С — емкость, измеряется в Фарадах
Но, одно то мы не учли… Сопротивление выводов и пластин с частотой не меняется! Так… и если пораскинуть мозгами, то получается, что на бесконечной частоте сопротивление конденсатора будет равняться его ESRу? Получается, наш конденсатор превращается в резистор? А как ведет себя резистор в цепи переменного тока? Да точно также как и в цепи постоянного тока: греется! Следовательно на этом резисторе будет рассеиваться мощность P в окружающую среду. А как вы помните, мощность через сопротивление и силу тока выражается формулой:
P=I2xR
где
I — это сила тока, в Амперах
R — сопротивление резистора ESR, в Омах
Значит, если ESR будет больше, то и мощность рассеивания тоже будет больше! То есть этот резистор будет хорошенько нагреваться.
Догоняете о чем я вам толкую?
Из всего выше сказанного можно сделать простенький вывод: конденсатор с большим ESR в высокочастотных цепях с большими токами будет нагреваться. Ну да ладно, пусть себе греется… Резисторы и микросхемы тоже ведь греются и ничего! Но весь косяк заключается в том, что с увеличением температуры конденсатора меняется и его емкость! Есть даже такой интересный параметр конденсатора, как ТКЕ или Температурный Коэффициент Емкости. Этот коэффициент показывает, насколько поменяется емкость при изменении температуры. А раз уже «плавает» емкость, то вслед за ней «плывет» и схема.
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
Рисунок 1.21.2. Вычисление энергии магнитного поля.
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
Ɛ=- L(dI/dt), где:
- Ɛ – ЭДС самоиндукции;
- L-индуктивность;
- I – сила тока;
- t – время.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)
Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.
Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.
Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.
Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.
Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:
где:
- n — повое число витков катушки;
- n1 — число витков катушки, указанное в описании;
- d— диаметр имеющеюся провода;
- d1 — диаметр провода, указанный в описании.
В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:
(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).
Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:
При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.
Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.
Рис. 2. Катушки индуктивности. Пример.
Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.
Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.
Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:
Новая катушка на каркасе с увеличенным диаметром:
Ошибка при пересчете составляет 0,25 мкГн, что вполне допустимо для расчетов в радиолюбительской практике.