Полное сопротивление трансформатора формула – Расчетные сопротивления трансформаторов — КиберПедия

Реактивное сопротивление трансформатора: формулы расчета

Мы привыкли считать, что все магнитные потоки в трансформаторе пронизывают обе обмотки и магнитопровод. Если бы существовал идеальный трансформатор, то это действительно так бы и происходило. К сожалению, в реальности часть магнитного потока преодолевает изоляционное пространство, выходит за пределы обмоток и замыкается в них (см. рис. 1). В результате возникает реактивное сопротивление трансформатора. Такое явление ещё называют рассеиванием магнитных потоков.

Рис. 1. Схема, иллюстрирующая рассеивание магнитных потоков

В катушках существуют и другие сопротивления, являющиеся причинами потерь мощности. Таковыми являются: внутреннее сопротивление материалов обмоток, и рассеивания, вызванные индуктивными сопротивлениями. Совокупность рассеиваний магнитных потоков называют внутренним сопротивлением или импедансом трансформатора.

Потери реактивных мощностей

Вспомним, как работает идеальный двухобмоточный трансформатор (см. рис. 2). Когда первичная обмотка окажется под переменным напряжением (например, от электрической сети), возникнет магнитный поток, который пронизывает вторичную катушку индуктивности. Под действием магнитных полей происходит возбуждение вторичных обмоток, в витках которых возникает ЭДС. При подключении активной мощности к прибору во вторичной цепи начинает протекать переменный ток с частотой входного тока.

Рис. 2. Устройство трансформатора

В идеальном трансформаторе образуется прямо пропорциональная связь между напряжениями в обмотках. Их соотношение определяется соотношением числа витков каждой из катушек. Если U1 и U2 – напряжения в первой и второй обмотке соответственно, а w1 и w2 – количество витков обмоток, то справедлива формула: U1 / U2 = w1 / w2.

Другими словами: напряжение в рабочей обмотке во столько раз больше (меньше), во сколько раз количество мотков второй катушки увеличено (уменьшено) по отношению к числу витков, образующих первичную обмотку.

Величину w1 / w2 = k принято называть коэффициентом трансформации. Заметим, что формула, приведённая выше, применима также для автотрансформаторов.

В реальном трансформаторе часть энергии теряется из-за рассеяния магнитных потоков (см. рис. 1). Зоны, где происходит концентрация потоков рассеяния обозначены пунктирными линиями. На рисунке видно, что индуктивность рассеяния охватывает магнитопровод и выходит за пределы обмоток.

Наличие реактивных сопротивлений в совокупности с активным сопротивлением обмоток приводят к нагреванию конструкции. То есть, при расчётах КПД необходимо учитывать импеданс трансформатора.

Обозначим активное сопротивление обмоток символами R1 и R2 соответственно, а реактивное – буквами X

1 и X2. Тогда импеданс первичной обмотки можно записать в виде:
Z1= R1+jX1. Для рабочей катушки соответственно будем иметь: Z2= R2+jX2, где j – коэффициент, зависящий от типа сердечника.
Реактивное сопротивление можно представить в виде разницы индукционного и ёмкостного показателя: X = RL – RC. Учитывая, что RL = ωL, а RC = 1/ωC, где ω – частота тока, получаем формулу для вычисления реактивного сопротивления: X = ωL – 1/ωC.

Не прибегая к цепочке преобразований, приведём готовую формулу для расчёта полного сопротивления, то есть, для определения импеданса трансформатора:

Суммарное сопротивление трансформатора необходимо знать для определения его КПД. Величины потерь в основном зависят от материала обмоток и конструктивных особенностей трансформаторного железа. Вихревые потоки в монолитных стальных сердечниках значительно больше, чем многосекционных конструкциях магнитопроводов. Поэтому на практике сердечники изготавливаются из тонких пластин трансформаторной стали. С целью повышения удельного сопротивления материала, в железо добавляют кремний, а сами пластины покрывают изоляционным лаком.

Для определения параметров трансформаторов важно найти активное и реактивное сопротивление, провести расчёты потерь холостого хода. Приведённая выше формула не практична для вычисления импеданса по причине сложности измерений величин индукционного и ёмкостного сопротивлений. Поэтому на практике пользуются другими методами для расчёта, основанными на особенностях режимов работы силовых трансформаторов.

Режимы работы

Двухобмоточный трансформатор способен работать в одном из трёх режимов:

вхолостую;
в режиме нагрузки;
в состоянии короткого замыкания.

Для проведения расчётов режимов электрических цепей проводимости заменяют нагрузкой, величина которой равна потерям при работе в режиме холостого хода. Вычисления параметров схемы замещения проводят опытным путём, переводя трансформатор в один из возможных режимов: холостого хода, либо в состояние короткого замыкания. Таким способом можно определить:

уровень потерь активной мощности при работе на холостом ходу;
величины потерь активной мощности в короткозамкнутом приборе;
напряжение короткого замыкания;
силу тока холостого хода;
активное и реактивное сопротивление в короткозамкнутом трансформаторе.

Параметры режима холостого хода

Для перехода в работу на холостом ходу необходимо убрать отсутствует нагрузку на вторичной обмотке, то есть – разомкнуть электрическую цепь. В разомкнутой катушке напряжение отсутствует. Главной составляющей тока в первичной цепи является ток, возникающий на реактивных сопротивлениях. С помощью измерительных приборов довольно просто найти основные параметры переменного тока намагничивания, используя которые можно вычислить потери мощности, умножив силу тока на подаваемое напряжение.

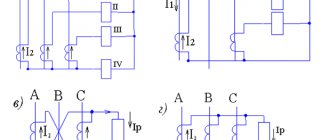
Схема измерений на холостом ходу показана на рисунке 3. На схеме показаны точки для подключения измерительных приборов.

Рис. 3. Схема режима холостого хода

Формула, применяемая для расчётов параметров реактивной проводимости, выглядит так: Вт = Iх%*Sном / 100* Uв ном2 Умножитель 100 в знаменателе применён потому, что величина тока холостого хода Iх обычно выражается в процентах.

Режим короткого замыкания

Для перевода трансформатора на работу в режиме короткого замыкания закорачивают обмотку низшего напряжения. На вторую катушку подают такое напряжение, при котором в каждой обмотке циркулирует номинальный ток. Поскольку подаваемое напряжение существенно ниже номинальных напряжений, то потери активной мощности в проводимости настолько малы, что ими можно пренебречь.

Таким образом, у нас остаются активные мощности в трансформаторе, которые расходуются на нагрев обмоток: ΔPk = 3* I1ном * Rт. Выразив ток I1 ном через напряжение Uка и сопротивление Rт, умножив выражение на 100, получим формулу для вычисления падения напряжения в зонах активного сопротивления (в процентах):

Активное сопротивление двухобмоточного силового трансформатора вычисляем по формуле:

Подставив значение Rт в предыдущую формулу, получим:

Вывод: в короткозамкнутом трансформаторе падение напряжения в зоне активного сопротивления (выраженная в %) прямо пропорционально размеру потерь активной мощности.

Формула для вычисления падения напряжения в зонах реактивных сопротивлений имеет вид:

Отсюда находим:

Величины реактивных сопротивлений в современных трансформаторах гораздо меньше активного. Поэтому можно считать что падение напряжения в зоне реактивного сопротивления Uк р ≈ Uк, поэтому для практических расчётов можно пользоваться формулой: XT = Uk*Uв ном2 / 100*Sном

Рассуждения, приведённые выше, справедливы также для многообмоточных, в том числе и для трёхфазных трансформаторов. Однако вычисления проводятся по каждой обмотке в отдельности, а задача сводится к решению систем уравнений.

Знание коэффициентов мощности, сопротивления рассеивания и других параметров магнитных цепей позволяет делать расчёты для определения величин номинальных нагрузок. Это, в свою очередь, обеспечивает работу трансформатора в промежутке номинальных мощностей.

www.asutpp.ru

Потери реактивных мощностей

Рис. 2. Устройство трансформатора

Обозначим активное сопротивление обмоток символами R1 и R2 соответственно, а реактивное – буквами X1 и X2. Тогда импеданс первичной обмотки можно записать в виде: Z1= R1+jX1. Для рабочей катушки соответственно будем иметь: Z2= R2+jX2, где j – коэффициент, зависящий от типа сердечника.

Реактивное сопротивление можно представить в виде разницы индукционного и ёмкостного показателя: X = RL – RC. Учитывая, что RL = ωL, а RC = 1/ωC, где ω – частота тока, получаем формулу для вычисления реактивного сопротивления: X = ωL – 1/ωC.

1.4. Определение сопротивления трансформатора.

Сопротивления трансформатора находятся по данным опыта короткого замыкания. Схема опыта показана на рисунке.

Из схемы опыта короткого замыкания видно, что напряжение короткого замыкания равно при номинальной нагрузке трансформатора.

Умножив на

числитель и знаменатель, получим

У силовых трансформаторов

, поэтому для них с достаточной точностью принимают, что

В опыте короткого замыкания ваттметр показывает сумму потерь активной мощности в стали и в меди. Поскольку U

к в % составляет 5 – 17 %, то пропорциональный напряжению магнитный поток в стальном сердечнике невелик.

Потери активной мощности в стали приблизительно пропорциональны квадрату магнитного потока, поэтому в опыте короткого замыкания они очень малы и, или можно пренебречь.

В результате:

, откуда

или

1.5. Определение проводимостей трансформатора.

Проводимости gт и bт находятся по данным опыта холостого хода. Схема опыта показана на рисунке.

Ток холостого хода мал и составляет . Потери мощности, в первичной обмотке, зависящей от квадрата этого тока, незначительны, в результате чего принимают, что .

Потери в стали определяются выражением , где

– активная составляющая тока холостого хода, которая равна

Выраженные через потери мощности в стали равны

Токи холостого хода активная составляющая которых покрывает потери активной мощности в стальном сердечнике на гистерезис и вихревые токи, в 5 – 10 раз меньше реактивной составляющей. Приближённо принимают

Отсюда

окончательно имеем

Таким образом

Трёхобмоточные трансформаторы.

Понижающие подстанции иногда питают распределительные сети двух напряжений, например 10(6) и 35 кВ. Если нагрузки этих сетей соизмеримы, то целесообразно применять трёхобмоточные трансформаторы с двумя вторичными обмотками вместо установки двух двухобмоточных трансформатора.

2.1. Соединение обмоток трёхобмоточных трансформаторов.

У силовых трансформаторов обмотки ВН и СН соединяются в звезду, обмотка НН в треугольник. Соответственно группа соединения у/у/Д-0-11.

На тяговых подстанциях для совместного питания тяги и района устанавливают трёхобмоточные трансформаторы.

Их первичная обмотка соединяется в звезду, а тяговая в треугольник. Соединение районной обмотки зависит от её напряжений. Если она имеет напряжение 11(6,6 кВ), то соединяют в треугольник, при напряжении 38,5 кВ – в звезду.

studfile.net

Режимы работы

Двухобмоточный трансформатор способен работать в одном из трёх режимов:

вхолостую;
в режиме нагрузки;
в состоянии короткого замыкания.

уровень потерь активной мощности при работе на холостом ходу;
величины потерь активной мощности в короткозамкнутом приборе;
напряжение короткого замыкания;
силу тока холостого хода;
активное и реактивное сопротивление в короткозамкнутом трансформаторе.

Параметры режима холостого хода

Рис. 3. Схема режима холостого хода

Режим короткого замыкания

Активное сопротивление двухобмоточного силового трансформатора вычисляем по формуле:

Подставив значение Rт в предыдущую формулу, получим:

Формула для вычисления падения напряжения в зонах реактивных сопротивлений имеет вид:

Отсюда находим:

Расчетные формулы основных параметров трансформаторов

Представляю вашему вниманию таблицу с расчетными формулами для определения основных параметров силовых трансформаторов, а также таблицу коэффициента изменения потерь kн.п. в трансформаторах.

Таблица 1 – Расчетные формулы для определения основных параметров трансформаторов

Наименование величин	Формулы	Обозначение
Токи обмоток	I1, I2 — токи первичной и вторичной обмоток, А; U1, U2 — то же линейное напряжение, В;
Коэффициент трансформации	w1, w2 – числа витков одной фазы обмоток
Приведение величин вторичной обмотки к первичной	Приведенные величины обозначают штрихом
Сопротивление короткого замыкания	rк, хк, zк – активные, реактивные и полное сопротивления КЗ фазы трансформатора
Активные потери мощности в трансформаторе при нагрузке	∆Рх – активные потери холостого хода, кВт; ∆Рк – активные нагрузочные потери в обмотках при номинальном токе, кВт; kз – коэффициент загрузки; Sт.ном. – номинальная мощность трансформатора.
Приведенные активные потери мощности в трансформаторе при нагрузке	S – фактическая нагрузка трансформатора; kи.п. – коэффициент изменения потерь, кВт/квар; ∆Qх – реактивные потери мощности холостого хода; ∆Qк – реактивные потери мощности КЗ; Значения kи.п. даны ниже.
Напряжение КЗ	Uк – напряжение КЗ, В или %; Uк.а, Uк.х – активная и реактивная составляющие напряжения КЗ, В или %.
Мощность и ток КЗ трансформатора	Sк –мощность КЗ, кВА
Число витков первичной обмотки	U1ф – фазное напряжение первичной обмотки, В Ф – фазный поток; Ф = Вст*Qст мкс; Вст –индукция в стержне; Вст = 13 – 14,5 103 Гс; Qст – активное сечение стержня, см2
Активное и реактивное сопротивление двухобмоточного трансформатора, Ом
Падение напряжения в обмотках трансформатора при нагрузке	Если нагрузка смешанная (активная и индуктивная), то вторым членом можно пренебречь
Потери напряжения при пуске асинхронного короткозамкнутого двигателя (приближенно)	∆U – потеря напряжения, %; Sдв. – номинальная мощность двигателя, кВА; S2 – мощность других потребителей, присоединенных к шинам трансформаторов, кВА; Ki – кратность пускового тока относительно номинального.
КПД трансформатора

raschet.info

Определение обмоток визуальным осмотром.

При визуальном осмотре трансформатора обращают внимание на его внешний защитный слой изоляции, потому как у некоторых моделей на внешнем слое изображают электрическую схему с обозначением всех обмоток и выводов; у некоторых моделей выводы обмоток только маркируют цифрами. Также можно встретить старые отечественные трансформаторы, на внешнем слое которых указывают маркировку в виде цифрового кода, по которому в справочниках для радиолюбителей есть вся информация о конкретном трансформаторе.

Если трансформатор попался без опознавательных знаков, то обращают внимание на диаметр обмоточного провода, которым намотаны обмотки. Диаметр провода можно определить по выступающим выводам концов обмоток, выпущенных для закрепления на контактных лепестках, расположенных на элементах каркаса трансформатора. Как правило, первичную обмотку мотают проводом меньшего сечения, по отношению к вторичной. Диаметр провода вторичной обмотки всегда больше.

Исключением могут быть повышающие трансформаторы, работающие в схемах преобразователей напряжения и тока. Их первичная обмотка выполнена толстым проводом, так как генерирует высокое напряжение во вторичной обмотке. Но такие трансформаторы встречаются очень редко.

При изготовлении трансформаторов первичную обмотку, как правило, мотают первой. Ее легко определить по выступающим концам выводов обмотки, расположенных ближе к магнитопроводу. Вторичную обмотку наматывают поверх первичной, и поэтому концы ее выводов расположены ближе к внешнему слою изоляции.

В некоторых моделях сетевых трансформаторов, используемых в блоках питания бытовой радиоаппаратуры, обмотки располагают на пластмассовом каркасе, разделенном на две части: в одной части находится первичная обмотка, а в другой вторичная. К выводам первичной обмотки припаивают гибкий монтажный провод, а выводы вторичной обмотки оставляют в виде обмоточного провода.

Сопротивление элементов схемы замещения в сети 0,4 кВ

Содержание

Для того чтобы рассчитать токи КЗ в сети до 1000 В, следует первоначально составить схему замещения, которая состоит из всех сопротивлений цепи КЗ. Активные и индуктивные сопротивления всех элементов схемы замещения выражают в миллиомах (мОм).

Как определять сопротивления отдельных элементов схемы замещения, об этом вы и узнаете в этой статье.

Активные и индуктивные сопротивления питающей энергосистемы рассчитывают на стороне ВН понижающего трансформатора и приводят к стороне НН по формуле 2-6 [Л3. с. 28].

На практике можно не учитывать активное сопротивление энергосистемы, а значение индуктивного сопротивления приравнивать как к полному сопротивлению энергосистемы (на точность расчетов это никак не скажется). В этом случае значение (в Омах) индуктивное (полное) сопротивление энергосистемы определяется по формуле 2-7 [Л3. с. 28].

После того как определили индуктивное сопротивление системы по формуле 2-7 [Л3. с. 28], данное сопротивление нужно привести к стороне НН по формуле 2-6 [Л3. с. 28].

Индуктивное сопротивление системы, также можно определить по формулам представленных в ГОСТ 28249-93:

Как мы видим формула 1 из ГОСТ 28249-93 соответствует формулам 2-6, 2-7 из [Л3. с. 28].

Пример

Определить сопротивление энергосистемы, учитывая, что ток КЗ со стороны энергосистемы на зажимах ВН трансформатора 6/0,4 кВ составляет в максимальном режиме – 19 кА, в минимальном – 13 кА.

Решение

Определяем индуктивное сопротивление энергосистемы по формулам 2-6, 2-7.

Сопротивление энергосистемы в максимальном режиме, приведенное к напряжению 0,4 кВ:

Сопротивление энергосистемы в минимальном режиме, приведенное к напряжению 0,4 кВ:

Значения (в мОм) полного (zт), активного (rт) и индуктивного (хт) сопротивления понижающего трансформатора приведенных к стороне НН определяются по формулам: 2-8, 2-9, 2-10 [Л3. с. 28].

На большинстве трансформаторов 10(6)/0,4 кВ имеется возможность регулирования напряжения путем переключения без возбуждения (ПБВ) при отключенном от сети трансформаторе как со стороны высшего так и низшего напряжения. Напряжение регулируется со стороны высшего напряжения на величину ±2х2,5% от номинального значения.

Для трансформаторов с пределом регулирования ПБВ ±2х2,5%, полное сопротивление будет изменятся в пределах:

Значения индуктивного и активного сопротивления трансформатора по ГОСТ 28249-93 определяются по формулам:

raschet.info

Тема 2.2 Сопротивления и проводимости трансформаторов

И автотрансформаторов

Г-образная схема замещения трансформатора состоит из продольного сопротивления Z

т=
R
т+
jX
т и поперечной проводимости
Y
т=
g
т–
jb
т.

2.2.1. Сопротивления и проводимости

двухобмоточных трансформаторов.

Активное сопротивление R

т моделирует процесс потерь электроэнергии на нагрев обмоток трансформатора (потери в меди); индуктивное сопротивление
X
т – потери вызванные потоками рассеяния; активная проводимость
g
т – потери на перемагничивание и вихревые токи (потери в стали); реактивная (индуктивная) проводимость
b
т – потери обусловленные намагничивающей мощностью. Необходимо отметить, что индуктивное сопротивление трансформаторов во много раз больше активного, особенно это касается мощных трансформаторов [5].

Параметры Г-образной схемы замещения трансформатора определяются по следующим формулам:

, (2.8)

, (2.9)

, (2.10)

. (2.11)

В этих формулах S

ном – номинальная мощность трансформатора;
U
– напряжение, к которому приводятся параметры трансформатора (обычно номинальное напряжение обмотки высшего напряжения); Δ
P
к – потери короткого замыкания;
u
к – напряжение короткого замыкания, %; Δ
P
х — потери холостого хода;
I
х – ток холостого хода, %. Последние четыре параметра являются каталожными данными трансформатора.

2.2.2. Сопротивления и проводимости

трёхобмоточных трансформаторов.

Эквивалентная схема трехобмоточного трансформатора показана на рисунке 2.1.

Рисунок 2.1 Г-образная схема замещения одной фазы трехобмоточного трансформатора

Для трехобмоточных трансформаторов заводами даются потери короткого замыкания для худшего случая, т.е. для случая максимальных потерь ΔР

к. макс.

Активное сопротивление каждого луча трехобмоточного трансформатора определяется по следующей формуле

. (2.12)

Для трехобмоточных трансформаторов напряжения короткого замыкания даются заводами для каждой пары обмоток в процентах от номинального. Поэтому индуктивное сопротивление каждого луча, %, приходится определять отдельно по выражениям:

; ; . (2.13)

Для определения значений напряжения короткого замыкания между обмотками одна из обмоток закорачивается, к другой подключается вольтметр, а третья остается разомкнутой. Тогда вольтметр показывает напряжение короткого замыкания между двумя первыми обмотками u

к (В–С), если по ним протекает номинальный ток
I
ном. Таким образом, можно записать

к (В–Н) =
u
к. В +
u
к. Н;

к (В–С) =
u
к. В +
u
к. С; (2.14)

к (С–Н) =
u
к. С +
u
к. Н.

Решив совместно уравнения (2.14), можно найти напряжение короткого замыкания, %, для каждого луча:

к. В = 0,5(
u
к (В–С) +
u
к (В–Н) –
u
к (С–Н));

к. С = 0,5(
u
к (В–С) +
u
к (С–Н) –
u
к (В–Н)); (2.15)

к. Н = 0,5(
u
к (В–Н) +
u
к (С–Н) –
u
к (В–С)).

Подставив эти значения в выражение (2.13), определим индуктивное сопротивление каждого луча трансформатора.

Проводимости не зависят от числа обмоток в трансформаторе и определяются так же, как и для двухобмоточного по (2.10) и (2.11).

2.2.3. Сопротивления и проводимости автотрансформаторов.

Пересчёт параметров трансформаторов к номинальной мощности

Автотрансформатором (рисунок 2.2) принято называть такой трансформатор, у которого обмотка среднего (С) напряжения является частью обмотки высшего (В) напряжения [5].

Рисунок 2.2. Схема соединения обмоток автотрансформатора

Таким образом, обмотка высшего напряжения состоит из двух частей: последовательной обмотки (пос) между В

и
С
, по которой протекает только ток высшего напряжения
IB
, и общей обмотки (об) между
С
и 0, по которой в противоположных направлениях протекают токи высшего и среднего напряжений, т. е. их разность:

об =
I
С –
I
В. (2.16)

Обмотка низшего (Н) напряжения имеет магнитную связь с остальными обмотками. Мощность обмотки НН составляет только 20–50%, если принять мощность каждой из обмоток В и С равной 100%. Обмотка Н всегда соединена в треугольник для компенсации токов третьих гармоник. Иногда к этой обмотке ничего не присоединено.

Автотрансформаторы имеют следующие преимущества: меньшие стоимость, габариты, массу и потери мощности. Недостаток – электрическая связь между стороной высшего и среднего напряжений, например, если трансформатор заземлен для стороны высшего напряжения, то он будет заземлен и для стороны среднего напряжения.

Автотрансформатор можно получить из трансформатора с отдельно работающими обмотками, последовательной и общей, соединением этих обмоток электрически. При этом все процессы в обмотках стали автотрансформатора и трансформатора (рисунок 2.1, а, б) одинаковы. Поэтому одинаковы их габариты, потери в обмотках и стали и т. д. Однако мощность, передаваемая через автотрансформатор, больше, чем через трансформатор.

Активные сопротивления R

т.
Для автотрансформаторов потери активной мощности даются заводами не максимальные ΔР
к м для всего трансформатора, как это было при трехобмоточных трансформаторах, а для каждой пары обмоток, т. е. Δ
Р
(В–С), Δ
Р
(В–Н), Δ
Р
(С–Н). Чтобы определить активные сопротивления лучей звезды
R
т В и
R
т С в схеме замещения трехобмоточного автотрансформатора можно для инженерных расчетов с достаточной точностью (пренебрегая мощностью цепи намагничивания) пользоваться выражениями, аналогичными (2.15):

ΔР

к В = 0,5(Δ
Р
к (В–С) + Δ
Р
к (В–Н) – Δ
Р
к (С–Н));

ΔР

к С = 0,5(Δ
Р
к (В–С) + Δ
Р
к (С–Н) – Δ
Р
к (В–Н)). (2.17)

Соответственно

т В = Δ
Р
к В
U
2/
S
2ном;

т С = Δ
Р
к С
U
2/
S
2ном. (2.18)

Сопротивление R

т находится в зависимости от мощности этой обмотки так же, как активные сопротивления в трехобмоточных трансформаторах.

Индуктивные сопротивления Х

т.
Эти сопротивления определяются так же, как для трехобмоточных трансформаторов по (2.13) и (2.15).
Проводимости не зависят от характера соединения обмоток или их числа и определяются так же, как и для двухобмоточных трансформаторов по (2.10) и (2.11).

РАЗДЕЛ 3. АНАЛИЗ РЕЖИМОВ РАБОТЫ СЕТЕЙ

Расчет токов однофазного кз в сети 0,4 кВ

В данной статье речь пойдет об определении величины тока однофазного тока к.з. в сетях 0,4 кВ с глухозаземленной нейтралью.

Данный вопрос очень актуален, так как электрические сети 0,4 кВ, являются наиболее распространёнными.

В настоящее время существует два метода расчета однофазного КЗ – точный и приближенный и оба метода основаны на методе симметричных составляющих.

Точный метод определения тока однофазного КЗ

1.1 Точный метод определения тока однофазного КЗ, представлен в ГОСТ 28249-93 формула 24, и рассчитывается по формуле:

Используя данный метод можно с большой степенью точности определять токи КЗ при известных сопротивлениях прямой, обратной и нулевой последовательности цепи фаза-нуль.

К сожалению, на практике данный метод не всегда возможно использовать, из-за отсутствия справочных данных на сопротивления прямой, обратной и нулевой последовательности для кабелей с алюминиевыми и медными жилами с учетом способов прокладки фазных и нулевых проводников.

Приближенный метод определения тока однофазного КЗ

2.1 Приближенный метод определения тока однофазного кз при большой мощности питающей энергосистемы (Хс < 0,1Хт), рассчитывается по формуле [Л1, с 4 и Л3, с 39]:

где:

Uф – фазное напряжение сети, В;
Zт – полное сопротивление трансформатора току однофазного замыкания на корпус, Ом;
Zпт – полное сопротивление петли фаза-нуль от трансформатора до точки КЗ, Ом.

2.2 Если же питающая энергосистема имеет ограниченную мощность, то тогда ток однофазного кз определяется по формуле 2-26 [ Л3, с 39]:

2.3 Значение Z∑ определяется по таблице 2.9 или можно определить по формуле 2-25 [ Л3, с 39]:

где: х1т и r1т; х2т и r2т; х0т и r0т — индуктивное и активное сопротивления трансформатора токам прямой, обратной и нулевой последовательности, мОм. Принимаются по таблице 2.4 [Л3, с 29].

Значение Zт/3 для различных трансформаторов с вторичным напряжением 400/230 В, можно принять по таблицам 2, 3, 4 [Л1, с 6,7].

Сопротивления контактов шин, аппаратов, трансформаторов тока в данном методе не учитываются, поскольку арифметическая сумма Zт/3 и Zпт создает не который запас.

2.4 Полное сопротивление трансформатора Zт, определяется по формуле 2-24 [Л3, с 39]:

2.5 Полное сопротивление петли фаза-нуль, определяется по формуле 2-27 [Л3, с 40]:

где:

Zпт.уд. – полное удельное сопротивление петли фаза-нуль для каждого участка от трансформатора до места КЗ определяется по таблицам 2.10 – 2.14 [Л3, с 41,42] или по таблицам [Л2], мОм/м;
l – длина участка, м.

Ниже представлены справочные таблицы со значениями удельного сопротивления петли фаза-нуль для различных кабелей и шинопроводов согласно [Л3, с 41,42].

Справочные таблицы 7, 10 со значениями активных сопротивления медных и алюминиевых проводов, кабелей [Л1, с 6, 14].

raschet.info