Резонанс – что это такое
Резонанс в физике – это частотно-избирательный отклик системы колебаний на внешние силы, которые периодически воздействуют на систему. Проявляется это воздействие в резком увеличении амплитуды движений этих колебаний, когда частота внешней воздействующей силы совпадает с некоторыми, характерными для данной колебательной системы, частотами.
Важно! Суть резонирования заключается в резком увеличении амплитуды колебаний при совпадении значения частоты силы, воздействующей на систему извне, с собственной частотой колебаний этой системы.
Тупое и острое резонирование
Чтобы далее говорить о явлении резонирования, следует понять, что такое колебания и частота. Колебания – это процесс изменения состояний колебательной системы, который повторяется через определенные промежутки времени и происходит вокруг точки равновесия. В пример можно привести раскачивание на качелях. Произойти резонирование частот может только там, где есть колебательные движения. Причем совсем неважно, к какому именно виду относятся колебания: электрические, звука, механические.
Виды колебательных движений
Процесс колебаний характеризуют частота и амплитуда. Простыми словами, на примере качели можно сказать, что амплитуда – это высшая точка, которую они достигают. Частота колебаний отвечает за скорость достижения качелями этой точки.
Возвращаясь к примеру с качелями, можно сказать, что когда они раскачиваются, система колебаний совершает вынужденные колебания. Увеличить амплитуду этих колебаний можно путем воздействия на эту систему определенным образом. То есть, если толкать качели с определенной силой и в определенное время, то можно сильно раскачать их без применения больших усилий.
Это явление и будет называться резонансом: частота воздействий извне будет совпадать с частотой колебаний в системе, и вследствие этого будет увеличиваться амплитуда.
Резонирование напряжений в электроцепи
Примеры резонанса в жизни
Толчок человека на качелях является распространенным примером этого явления. Загруженные качели, маятник имеют собственную частоту колебаний и резонансную частоту, которая сопротивляется толканию быстрее или медленнее.
Примером является колебание снарядов на детской площадке, которое действует как маятник. Нажатие человека во время качания с естественным интервалом колебания приводит к тому, что качели идут все выше и выше (максимальная амплитуда), в то время как попытки делать качание с более быстрым или медленным темпом создают меньшие дуги. Это связано с тем, что энергия, поглощаемая колебаниями, увеличивается, когда толчки соответствуют естественным колебаниям.
Отклик широко встречается в природе и используется во многих искусственных устройствах. Это механизм, посредством которого генерируются практически все синусоидальные волны и вибрации. Многие звуки, которые мы слышим, например, когда ударяются жесткие предметы из металла, стекла или дерева, вызваны короткими колебаниями в объекте. Легкое и другое коротковолновое электромагнитное излучение создается резонансом в атомном масштабе, таким как электроны в атомах. Другие условия, в которых могут применяться полезные свойства этого явления:
- Механизмы хронометража современных часов, колесо баланса в механических часах и кварцевый кристалл в часах.
- Приливной отклик залива Фанди.
- Акустические резонансы музыкальных инструментов и человеческого голосового тракта.
- Разрушение хрустального бокала под воздействием музыкального правого тона.
- Фрикционные идиофоны, такие как изготовление стеклянного предмета (стекла, бутылки, вазы), вибрируют, при потирании вокруг его края кончиком пальца.
- Электрический отклик настроенных схем в радиостанциях и телевизорах, которые позволяют избирательно принимать радиочастоты.
- Создание когерентного света оптическим резонансом в лазерной полости.
- Орбитальный отклик, примером которого являются некоторые луны газовых гигантов Солнечной системы.
Материальные резонансы в атомном масштабе являются основой нескольких спектроскопических методов, которые используются в физике конденсированных сред, например:
- Электронный спиновой.
- Эффект Мёссбауэра.
- Ядерный магнитный.
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
Рис. 1. Резонанс в электрической цепи
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).
Рис. 2. Графики зависимости параметров тока от падения реактивного сопротивления
Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).
Рис. 3. Последовательный колебательный контур
Рис. 4. Параллельный колебательный контур
В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:
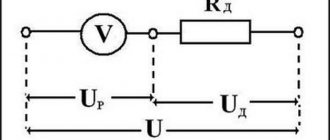
Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
K = Uвых / Uвх = UC0 / U = Q
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Будет интересно➡ Что такое ограничитель перенапряжения и как он работает?
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Разрушительная сила звука
Многие наверняка слышали о том, что винный бокал можно разбить голосом оперной певицы. Если вы слегка ударите бокал ложкой, он будет «звонить», как колокол, на своей резонансной частоте. Если на стекло оказывается звуковое давление на определенной частоте, оно начинает вибрировать. По мере того как стимул продолжается, вибрация в бокале накапливается до тех пор, пока он не разрушится, когда будут превышены механические пределы.
Примеры полезного и вредного резонанса повсюду. Микроволны окружают все вокруг, от микроволновой печки, которая разогревает пищу без применения внешнего тепла, до вибраций в земной коре, приводящих к разрушительным землетрясениям.
2) Когда мы настраиваем радиоприемник, мы меняем собственную частоту колебательного контура, добиваясь её совпадения с частотой передающей радиостанции.
3) Когда скрипач проводит смычком по струне, энергия передается струне (крохотные зацепочки на конском волосе, натянутом на смычке, дергают струну) . Возникает так называемый параметрический резонанс. Струна начинает колебаться со своей собственной частотой, зависящей от длины, натяжения и массы. Амплитуда колебания не возрастает до бесконечности, так как энергия колеблющейся струны тут же расходуется на создание звуковых волн, улетающих в пространство. Получается баланс: сколько энергии тратит скрипач, столько же и рассеивается в самой струне и тратится на излучение звука.
Явление резонанса заключается в том, что амплитуда установившихся вынужденных колебаний достигает наибольшего значения, когда частота вынуждающей силы равна собственной частоте колебательной системы.
Отличительной особенностью вынужденных колебаний является зависимость их амплитуды от частоты изменения внешней силы. Для изучения этой зависимости можно воспользоваться установкой, изображенной на рисунке:
На кривошипе с ручкой укреплен пружинный маятник. При равномерном вращении ручки на груз через пружину передается действие периодически изменяющейся силы. Изменяясь с частотой, равной частоте вращения ручки, эта сила заставит груз совершать вынужденные колебания. Если вращать ручку кривошипа очень медленно, то груз вместе с пружиной будет перемещаться вверх и вниз так же, как и точка подвеса О. Амплитуда вынужденных колебаний при этом будет невелика. При более быстром вращении груз начнет колебаться сильнее, и при частоте вращения, равной собственной частоте пружинного маятника (ω = ωсоб), амплитуда его колебаний достигнет максимума. При дальнейшем увеличении частоты вращения ручки амплитуда вынужденных колебаний груза опять станет меньше. Очень быстрое вращение ручки оставит груз почти неподвижным: из-за своей инертности пружинный маятник, не успевая следовать изменениям внешней силы, будет просто дрожать на месте.
Явление резонанса можно продемонстрировать и с нитяными маятниками. Подвесим на рейке массивный шар 1 и несколько маятников, имеющих нити разной длины. Каждый из этих маятников имеет свою собственную частоту колебаний, которую можно определить, зная длину нити и ускорение свободного падения.
Явление резонанса в цепях переменною тока
Цель работы. Изучить явление резонанса в цепях переменною тока. Определить резонансные частоты и параметры цепей для различных типов соединений.
1. Изучение резонанса напряжений в цепях переменного тока
Резонанс напряжений возникает при определенных условиях в цепи переменного тока с последовательно соединенным активным сопротивлением R, соленоидом индуктивностью L и конденсатором емкостью С (рис. 1).
Пусть цепь подключена к источнику синусоидального напряжения U, которое изменяется с циклической частотой . По закону Кирхгофа для данной цепи
или
Дифференциальное уравнение (2) можно решить различными методами, используем для ею решения метод векторных диаграмм.
Эту же задачу можно решить методом векторных диаграмм. Этот метод основан на том, что синусоидально изменяющуюся со временем величину (например, графически можно предоставить в виде проекции на вертикальную ось вращающегося вектора, длина которого равна максимальному (амплитудному) значению . Угловая скорость вращения вектора равна циклической частоте а угол, образованный вектором с горизонтальной осью в начальный момент времени, равен начальной фазе синусоидальной величины (рис. 2).
Пользуясь методом векторных диаграмм, можно алгебраическое сложение мгновенных значений синусоидально изменяющихся со временем величин одинаковой частоты заменить геометрическим сложением векторов их представляющих. Тогда длина результирующего вектора даст амплитуду результирующей синусоиды, а угол, образованный им с горизонтальной осью – ее начальную фазу.
Возможно вам будут полезны данные страницы:
| Мощность цепи синусоидального тока |
| Коэффициент мощности и его экономическое значение |
| Характерные особенности резонанса напряжений |
| Трехфазные цепи |
Построим векторную диаграмму напряжений нашей цепи. Для этого заметим, что если источник в цепи создает синусоидальное напряжение и, изменяющееся с частотой , то ток в цепи будет также синусоидальным с той же частотой. Поскольку ток в последовательной цепи на всех участках одинаков, то удобнее принять начальную фазу тока равной нулю, а напряжения на участках цепи рассчитать при этом условии.
где – амплитуда тока. Тогда мгновенное значение напряжения на активном сопротивлении
т.е. совпадает по фазе с силой тока, где – амплитуда напряжения на активном сопротивлении R.
Мгновенное значение напряжения на индуктивности
т.е. опережает но фазе силу тока на , где – амплитуда напряжения на катушке индуктивности L.
Мгновенное значение напряжения на емкости
т.е. отстает по фазе от силы тока на , где – амплитуда напряжения на емкости С.
При построении векторной диаграммы вектор тока откладывается горизонтально, поскольку он одинаков во всех последовательно соединенных элементах цепи R. L и С. Вектора, соответствующие напряжениям, представляются с учетом соответствующего сдвига фаз относительно тока (рис. 3).
Первый из них совпадает с направлением вектора, соответствующего току, а второй и третий повернуты на углы . относительно тока. При сложении этих векторов получается результирующий вектор, длина которого дает амплитуду приложенного напряжения , а угол – разность фаз напряжения и тока.
Отсюда получим выражение для силы тока
Величина называется полным сопротивлением (импедансом) цепи, – индуктивным сопротивлением. – емкостным сопротивлением, а – реактивным сопротивлением цепи. Это выражение представляет собой закон Ома для данной цени, поскольку связывает амплитудные значения тока и напряжения постоянным коэффициентом Z (при постоянных R, L, С и ).
Сдвиг фаз между током и напряжением также определяется из векторной диаграммы:
Анализ выражений (9) и (10) показывает, что частоту (при постоянных значениях L и С) можно подобрать так, чтобы индуктивное и емкостное сопротивления были одинаковыми:
При этом реактивное сопротивление X цепи обращается в нуль, полное сопротивление Z минимально и равно только активному сопротивлению (Z = R), сила тока и напряжение совпадают по фазе , амплитуда силы тока достигает максимальной величины:
При этих условиях амплитудные значения напряжений на емкости и индуктивности противоположны по фазе и равны по величине
и, поэтому это явление называется резонансом напряжений (на индуктивности и емкости), а частота при которой достигается резонанс-резонансной частотой. Она находится из соотношения (11):
Период колебаний тока и напряжений при резонансе
Поскольку напряжения на индуктивности и емкости изменяются в противоположных фазах, то суммарное напряжение на участке индуктивность-емкость равно нулю, хотя напряжения на индуктивности и емкости по отдельности могут быть весьма значительными и даже большими, чем напряжение на концах всей цепи.
Действительно, если то, как следует из выражения (11), , что может быть опасным для цепи.
Условие резонанса может быть достигнуто разными способами:
1) подбором частоты при постоянных значениях L и С;
2) подбором индуктивности L при постоянных значениях и С;
3) подбором емкости С при постоянных значениях и L.
Зависимость амплитуды силы тока от частоты графически изображена на рис. 4. Представленные кривые называются резонансными. Чем меньше активное сопротивление R, тем круче и острее кривая, а чем больше R, тем кривая более пологая.
Зависимость сдвига фаз от частоты графически изображена на рис. 5, где приведены две кривые для разных значений активного сопротивления R. При частотах сдвиг фаз , т.е. в цени преобладает емкостное сопротивление. При сдвиг фаз , и в цепи преобладает индуктивное сопротивление. При резонансе величина
Все рассмотренные соотношения справедливы и для действующих значений и U, так как последние отличаются от амплитудных только постоянным множителем. Например, для гармонически изменяющихся величин
Будет интересно➡ Что такое реактивная мощность и как её рассчитать?
Типы резонанса
В физике существует большое количество видов резонанса. Все они чем-то схожи и чем-то различны, а именно – своими признаками и природой появления. Среди них можно выделить:
- механический и акустический резонансы;
- электрический;
- оптический;
- орбитальные колебания;
- атомный, частичный и молекулярный.
График процесса в колебательном контуре
В следующих подразделах будет более подробно описан каждый из этих видов.
Механический и акустический
Наиболее популярным и очевидным механическим видом будут резонирующие качели, которые были упомянуты раньше. Если толкать их в определенные моменты с учетом их частоты, то размах их движения увеличится или затухнет, если силу не прикладывать.
Основаны механические резонаторы на преобразовании потенциальной энергии в кинетическую и обратно. Если рассматривать маятник, то вся его энергия – потенциальная в состоянии покоя. Она преобразуется в кинетическую, когда он проходит нижнюю точку на своей максимальной скорости.
Приборы для организации резонанса
Важно! Некоторые механические системы способны запасать потенциальную энергию и использовать ее в различных формах. В пример можно привести пружину, которая запасет сжатие, являющееся энергией связи атомов
Акустический тип резонирования можно встретить в некоторых музыкальных инструментах по типу гитары, скрипки, пианино. Они имеют основную резонансную частоту, которая зависит от длины, массы и силы натяжения струн.
Акустическое резонирование помогает людям найти дефекты в трубопроводе
Кроме основной частоты, струны этих музыкальных инструментов обладают резонансом на высших гармонических колебаниях основной частоты. Если струну дернуть, то она начнет колебаться на всех частотах, которые присущи данному импульсу, но частоты, несовпадающие с резонансом, очень быстро затухнут, и человеческое ухо услышит только гармонические колебания, являющиеся нотами.
Акустические системы, микрофоны и громкоговорители не терпят резонанса отдельных частей своего корпуса, так как это снижает равномерность их амплитудно-частотной характеристики и ухудшает качество воспроизведения звуков.
Струны создают акустический резонанс
Резонанс электрический
В электронике резонанс также имеется. Им называется состояние или режим пассивной электроцепи, содержащей катушки и конденсаторы, при котором ее входное реактивное электросопротивление и проводимость будут нулевыми. Это означает, что при резонансе ток на входе в цепь, если он есть, будет совпадать по фазе с напряжением.
В электричестве резонирование достигается тогда, когда индукция и емкость реакции уравновешиваются. Это равенство и позволяет энергии производить циркуляцию между индуктивными элементами и их магнитным полем, и полем электрического типа в конденсаторе.
Сам механизм резонанса основан на том, что МП индуктивности создает электроток, который заряжает конденсатор, разрядка его и создает это магнитное поле. Простейшее устройство, основанное на этом взаимодействии, – колебательный контур, способный производить резонанс напряжений и токов.
Модель светового оптического резонирования
Оптический резонанс
И в оптическом диапазоне есть резонанс. Один из самых популярных его примеров – резонатор Фабри-Перо. Он образован несколькими зеркалами, между которыми устанавливается так называемая резонирующая стоячая волна. Кроме этого используются кольцевые системы резонирования с бегущей волной и микроскопические резонаторы со стоячими волнами.
Схема колебательного контура
Орбитальные колебания
Колебания в астрофизике представляют собой ситуации, когда есть два или более небесных объекта, которые имеют некоторые периоды обращения, соотносящиеся, как небольшие натуральные числа. В результате этого воздействия небесные объекты оказывают друг на друга постоянное гравитационное притяжение. Оно и производит стабилизацию их орбит.
Колебания есть и на орбитах небесных тел
Резонанс токов и напряжений
Механический резонанс
Параллельный контур используют, чтобы создать резонанс тока. Для выполнения отмеченных выше условий выбирают равные значения реактивных проводимостей (BL и Bc). По мере увеличения частоты общее сопротивление контура возрастает, что сопровождается уменьшением силы тока.
График изменения тока и проводимости, формулы для расчетов
В последовательном резонансном контуре устанавливают аналогичные функциональные компоненты. Эта схема при достижении резонансной частоты уменьшает сопротивление, что сопровождается существенным увеличением напряжения на реактивных составляющих, по сравнению с электродвижущей силой источника питания.
Резонанс напряжений в цепи переменного тока: график, электрическая схема и формула расчета
Виды резонансных явлений
Для вычисления параметров механической системы можно продолжить изучение маятника. Естественное движение качелей замедляется трением функциональных компонентов, сопротивлением воздуха. Чтобы предотвратить затухание колебаний нужно приложить внешнюю силу (F). Максимальную эффективность обеспечит совпадение частот. Ниже показан алгоритм расчета.
v = ((F* Δt)/m) * N,
- N – количество импульсов;
- m – суммарная масса груза.
(m*v2)/2 = m*g*h = m*g*L*(1-cos α).
Из этих сочетаний простыми преобразованиями получают две формулы для расчетов:
- N = (m/(F* Δt)) * √(2*g*L*(1-cos α));
- t (общее время для выполнения N колебаний) = N*T = (2π*m*L)/(F* Δt)) * √(2*(1-cos α)).
Подставив определенные исходные значения, вычисляют периодичность необходимых резонансных колебаний:
- m=100кг;
- F = 10Н;
- L = 200 см;
- Δt = 1 с;
- N = 34;
- t = 96;
- T = 2,8 с.
Явление резонанса может наблюдаться в цепях переменного тока при совпадении частот источника питания (сигнала) и реактивных компонентов контура. В этом случае можно рассматривать электрическое сопротивление, как аналог сил трения в механической системе.
Резонанс токов
Для создания необходимых условий можно применить параллельное соединение типовых элементов (R, L и C). Если обеспечить равенство импедансов реактивных составляющих, на определенной частоте суммарное значение токов в соответствующих цепях будет больше, по сравнению с током источника питания. Графика на рисунке демонстрирует векторное представление электрических параметров.
Xc = 1/(2π*f*C),
- Xc – сопротивление;
- f – частота;
- С – емкость.
XL = 2π*f*L.
Fрезонанса = 1/2π * √ (L*C).
Условия резонанса напряжений в последовательном контуре
Если применить трансформатор для образования связи между двумя колебательными контурами, расчет усложняется. Для создания необходимых условий обеспечивают равенство реактивных составляющих.
Резонансные кривые связанных контуров
Нелинейные системы
Если отсутствуют симметричные реакции на сторонние воздействия, резонансные явления проявляются особым образом. В частности, наличие в цепи катушки с ферритовым сердечником существенно усложняет точный расчет. В подобных материалах магнитные свойства определяются нелинейным распределением элементарных компонентов.
Слово resono в переводе с латыни значит отклик. Колеблющаяся система откликается на наружные колебательные влияния. При приближении частоты наружной к частоте своей собственной она отвечает резким повышением амплитуды своих вынужденных периодических отклонений от состояния равновесия.
Явление резонанса
Важно! Резонанс и унисон – это не одинаковые явления. Унисон – это совпадение звуков по тону
В этом случае не происходит увеличения амплитуды звуковых колебаний, а наступает «одноголосье» двух или нескольких источников звука.
Две струны могут звучать в унисон, если к ним одновременно прикладывать силу, приводящую к их колебаниям. Но одна может резонировать с другой в момент совпадения частот их колебаний и увеличивать громкость своего звучания.
Для чего используется резонанс
Как явление, резонанс напряжений часто используется в различных фильтрах электрического типа. Например, если есть необходимость устранения из сигнала передачи некоторой составляющей тока определенной частоты, то к приемнику параллельно подключают катушку и конденсатор, которые по отношению друг к другу соединены последовательно. В результате подобных действий электроток определенной резонансной частоты замкнется через цепочку дроссель-конденсатор и не попадет на приемник.
Колебательный контур
Важно! Сам по себе резонанс напряженности в электричестве — явление негативное, так как он способствует появлению перенапряжений на некоторых участках соединения и выводит из строя приборы.
Создание звуковых волн
Чтобы понять, что происходит, вам сначала нужно немного узнать о том, как звук проходит по воздуху. Звуковые волны создаются, когда что-то вызывает вибрацию молекул воздуха. Затем эта вибрация перемещается, как волна, наружу во всех направлениях. Когда волна проходит по воздуху, есть области, где молекулы сжимаются ближе друг к другу, и области, где молекулы вытягиваются дальше друг от друга. Расстояние между последовательными сжатиями или расширениями известно как длина волны. Частота измеряется в единицах Герца (Гц), а один Герц соответствует одной скорости сжатия волны в секунду.
Люди могут обнаруживать звуковые волны с частотами от 20 до 20 000 Гц! Однако они не все звучат одинаково. Некоторые звуки высокие и скрипучие, в то время как другие низкие и глубокие. То, что вы на самом деле слышите, – это разница в частоте. Итак, как частота относится к длине волны? Скорость звука немного меняется в зависимости от температуры воздуха, но обычно она составляет около 343 м/с. Поскольку все звуковые волны движутся с одинаковой скоростью, частота будет уменьшаться по мере увеличения длины волны и возрастать при уменьшении длины волны.
Принцип работы резонанса
Если сопротивление емкости и индуктивности подключить последовательно, то они вызовут в переменной цепи гораздо меньший сдвиг фаз, чем при отдельном включении. Говоря иначе, одновременное воздействие индуктивности и емкости создает компенсационные силы сдвига фаз. Полностью сдвиг компенсируется лишь в том случае уравнивания индуктивного и емкостного сопротивления, когда ωL = 1 / ωС.
Обратите внимание! Такая схема будет полностью характеризоваться активным R, то есть вести себя так, как будто в нее не подключены дроссель и конденсатор. Эта сопротивляемость будет равна сумме всех активных характеристик катушки и проводов соединения.
Вместе с этим рабочие напряжения дросселя и конденсатора будут равными и максимальными для данных условий. Если при маленьком активном сопротивлении данные характеристики значительно превысят общую напряженность цепи, то напряжения начнут резонировать.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
Катушки индуктивности
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Использование резонанса напряжений для передачи радиосигнала
Колебательный контур этого типа создают из последовательной комбинации трех базовых компонентов: резистор, конденсатор, индуктивность. Подходящим для резонанса условием является нулевое сопротивление цепи (комплексное). Для решения такой задачи следует изучить основные формулы.
Комплексное сопротивление Rк=R+j(wL-1/wC). Постоянный резистор (R) не зависит от частоты (w). Значит, придется оперировать с индукционными и емкостными элементами. Резонансный эффект получают при (wL-1/wC)=0. Для вычисления необходимых значений пользуются следующими расчетами:
- Lп=1/w2*C;
- Сп=1/w2*L;
- Wп=1/√L*C.
Из приведенных данных понятно, что корректировать можно любой из параметров при одновременном сохранении двух других. В практической схемотехнике удобнее работать с частотой, поэтому рассмотрим подробнее применение такого варианта.
Последовательный контур с графиками
На рисунках показаны условия возникновения резонанса напряжений. В точке, обозначенной w0, наблюдается равенство индуктивной и емкостной составляющих на определенной частоте. Небольшой сдвиг влево по оси обусловлен резистивным компонентом цепи.
Напряжение на конденсаторе (Uc) при частоте резонанса (W0) равно волновому сопротивлению колебательного контура (p=√L/C). Аналогичная разница потенциалов будет на клеммах катушки при частоте W0. Данная особенность объясняет особое название процесса – «резонанс напряжений». Также в электротехнических расчетах применяют следующие определения:
- Добротность – Q=p/R;
- Затухание – 1/Q.
Отмеченные свойства используют в радиоприемной и передающей аппаратуре. Выделение контуром определенного диапазона позволяет выполнять настройку станции на определенную частоту с определенной параметрами цепи погрешностью. Для контроля избирательности оценивают амплитуду сигнала относительно резонансной частоты. Уровень отклонения на 3 дБ в обе стороны (0,7 от максимума) называют полосой пропускания.
Амплитудно-частотная характеристика (АЧХ) и полоса пропускания
Последовательный колебательный контур
В колебательном контуре можно получить незатухающие колебания, если подключить его к источнику переменного тока. Если источник подключен последовательно с катушкой L и конденсатором С , то такая цепь называется последовательным колебательным контуром (рис.3).
При подключении внешнего источника к контуру в нем возникают не собственные (свободные) колебания контура, которые определяются значениями L и C, а с частотой напряжения источника U=Um∙sinω∙t. Такие колебания контура называются вынужденными. При вынужденных колебаниях элементы контура L, C будут иметь, в зависимости от частоты источника, определенные индуктивное XL и емкостное Xc сопротивления и соответствующие падения напряжения UL, Uc на них. Но контур имеет не только реактивные сопротивления, а еще и активное cопротивление потерь R, которое в основном равно сопротивлению провода катушки.
Так как в катушке и конденсаторе напряжения сдвинуты относительно тока на разные фазовые углы, то более наглядно их можно показать на векторных диаграммах (рис.4)
Будет интересно➡ УЗИП — устройство защиты от импульсных перенапряжений
Напряжение на индуктивном сопротивлении UL опережает ток на 90°, а напряжение на емкостном сопротивлении Uc отстает от тока на такой же угол 90° И получается, что векторы UL и Uc сдвинуты между собой на 180°, т.е. находятся в противофазе. Вектор напряжения на источнике U будет равен геометрической сумме напряжения вектора UR и вектора разницы напряжений реактивных сопротивлений UL-Uc.
Как видно из диаграммы рис.4а при UL > Uc напряжение внешнего источника опережает ток в колебательном контуре на угол φ<90° и находится выше оси абcцисс в зоне напряжений индуктивности. Значит в данном случае контур имеет сопротивление индуктивного характера. При UL < Uc (рис.4b) вектор источника уже будет отставать от вектора тока на угол φ<90° и контур будет иметь емкостное сопротивление.
Полное сопротивление контура Z будет равно:
Амплитудное значение тока Im определяется по формуле:
где Um – амплитудное напряжение источника, а ω -его угловая частота.
При выполнении равенства:
Физическое определение и привязка к объектам
Резонанс, согласно определению, можно понять как достаточно простой процесс:
- существует тело, находящееся в состоянии покоя или колеблющееся с определенной частотой и амплитудой;
- на него действует внешняя сила с собственной частотой;
- в случае, когда частота внешнего воздействия совпадает с собственной частотой рассматриваемого тела, возникает постепенное или резкое возрастание амплитуды колебаний.
Однако, на практике явление рассматривается в виде гораздо более сложной системы. В частности, тело может быть представлено не как единый объект, а сложная структура. Резонанс возникает при совпадении частоты внешней силы с так называемой суммарной эффективной колебательной частотой системы.
Резонанс, если рассматривать его с позиций физического определения, непременно должен приводить к разрушению объекта. Однако, на практике существует понятие добротности колебательной системы. В зависимости от ее значения, резонанс может приводить к различным эффектам:
- при низкой добротности система не способна в большой мере сохранять поступающие извне колебания. Поэтому наблюдается постепенное повышение амплитуды собственных колебаний до того уровня, когда сопротивление материалов или соединений не приводит к стабильному состоянию;
- высокая, близкая к единице добротность — самая опасная среда, в которой резонанс приводит, зачастую, к необратимым последствиям. Среди них может быть как механическое разрушение объектов, так и выделение большого количества тепла на уровнях, которые могут привести к возгоранию.
Также, резонанс возникает не только при действии внешней силы колебательного характера. Степень и характер реакции системы, в большой степени, отвечает за последствия действия направленных извне сил. Поэтому резонанс может возникнуть в самых разных случаях.
Параллельный колебательный контур
В параллельном колебательном контуре источник сигнала соединен с катушкой индуктивности и конденсатором параллельно (рис.11). При подаче переменного напряжения на контур происходит обмен энергиями между конденсатором и катушкой, но только в цепи внутри контура.
Для возникновения резонанса в нем, как и в последовательном контуре, необходимыми условиями являются равенство емкостного Хс и индуктивного ХL сопротивлений, а так же равенство частоты собственных колебаний контура и частоты колебаний источника тока. Только резонанс в параллельном колебательном контуром, в отличии от резонанса в последовательном контуре, называют резонансом тока.
В идеальном параллельном контуре (без потерь) вектора индуктивного Ic и емкостного тока IL (при ХL=Xc) при резонансе будут направлены в противоположные стороны и суммарный ток будет обращаться в нуль (рис.14a). А это значит, что сопротивление контура будет стремится к бесконечности. Но в реальном параллельном контуре существует сопротивление потерь R которое сосредоточено в основном в индуктивности (рис 14b) и поэтому, даже при резонансе ток в контуре уже не равен нулю, а равен активной составляющей тока в цепи катушки – Iк=IL+IR. Значит полное сопротивление контура Z будет уже не бесконечно, а равно:
Z=L/CR.
На рис.15 показан график характеристик зависимости тока Iк и полного сопротивления Z параллельного контура от частоты.
Можно сделать вывод: в цепи параллельного контура существуют два тока – ток от источника I протекающий через активное сопротивление потерь катушки и реактивный ток контура Iк . Внутри контура протекают реактивный ток довольно таки большой величины:
Iк=IQ,
но он потребляет малый ток от источника, который необходим лишь для компенсации потерь в контуре:
I=U/Z.
Добротность Q параллельного контура, в отличии от последовательного контура, показывает во сколько раз ток в элементах контура больше потребления тока источника:
Q ≈ Iк/I.
На рис.16 дан конкретный пример параллельного колебательного контура, где видно, что ток контура больше тока источника в Q раз.
В радиоприемниках так же применяется непосредственная связь колебательного контура с антенной, т.е. контур включен параллельно источнику сигнала (рис.17). Переменным конденсатором настраиваем контур на частоту сигнала нужной радиостанции. При резонансе контурный ток, вызванный нужной радиостанцией, становится относительно большим, а сопротивление контура тоже большим.Поэтому между точками а и b получается значительное напряжение. Для других станций контур представляет малое сопротивление и сигнал радиостанции уходит в “землю”.
Польза и вред резонанса
Для того чтобы сделать некий вывод о плюсах и минусах резонанса, необходимо рассмотреть, в каких случаях он может проявляться наиболее активно и заметно для человеческой деятельности.
Положительный эффект
Явление отклика широко используется в науке и технике. Например, работа многих радиотехнических схем и устройств основывается на этом явлении.
- Двухтактный двигатель. Глушитель двухтактного двигателя имеет особую форму, рассчитанную на создание резонансного явления. Оно улучшает работу двигателя засчет снижения потребления и загрязнения. Этот резонанс частично уменьшает несгоревшие газы и увеличивает сжатие в цилиндре.
- Музыкальные инструменты. В случае струнных и духовых инструментов звуковое производство происходит в основном при возбуждении колебательной системы (струны, колонны воздуха) до возникновения явления резонанса.
- Радиоприемники. Каждая радиостанция излучает электромагнитную волну с четко определенной частотой. Для его захвата цепь RLC принудительно подвергается вибрации с помощью антенны, которая захватывает все электромагнитные волны, достигающие ее. Для прослушивания одной станции собственная частота RLC-схемы должна быть настроена на частоту требуемого передатчика, изменяя емкость переменного конденсатора (операция выполняется при нажатии кнопки поиска станции). Все системы радиосвязи, будь то передатчики или приемники, используют резонаторы для «фильтрации» частот сигналов, которые они обрабатывают.
- Магнитно-резонансная томография (МРТ). В 1946 году два американца Феликс Блох и Эдвард Миллс Перселл самостоятельно обнаружили явление ядерного магнитного резонанса, также называемое ЯМР, которое принесло им Нобелевскую премию по физике.
Отрицательное воздействие
Однако не всегда явление полезно. Часто можно встретить ссылки на случаи, когда навесные мосты ломались при прохождении по ним солдат «в ногу». При этом ссылаются на проявление резонансного эффекта воздействия резонанса, и борьба с ним приобретает масштабный характер.
- Автотранспорт. Автомобилисты часто раздражаются шумом, который появляется при определенной скорости движения транспортного средства или в результате работы двигателя. Некоторые слабо закругленные части корпуса вступают в резонанс и излучают звуковые колебания. Сам автомобиль с его системой подвески представляет собой осциллятор, оснащенный эффективными амортизаторами, которые препятствуют возникновению острого резонанса.
- Мосты. Мост может выполнять вертикальные и поперечные колебания. Каждый из этих типов колебаний имеет свой период. Если стропы подвешены, система имеет очень разную резонансную частоту.
- Здания. Высокие здания чувствительны к землетрясениям. Некоторые пассивные устройства позволяют защитить их: они являются осцилляторами, чья собственная частота близка к частоте самого здания. Таким образом, энергия полностью поглощается маятником, препятствующим разрушению здания.
Следующая
РазноеКак проверить напряжение мультимером?
Виды и примеры резонанса
Только в самой физике различают такие виды резонанса как:
- Механический резонанс – это все те же вышеупомянутые качели, резонанс моста от проходящей роты солдат, резонанс колокольного звона и т. д. Одним словом, резонанс, вызванный механическими воздействиями.
- Акустический резонанс – это резонанс, благодаря которому работают все струнные музыкальные инструменты: гитара, скрипка, лютня, балалайка, банджо и т. д. К слову корпус музыкальных инструментов неспроста имеет свою форму. Звук, издаваемый струной при щипке, попадает внутрь корпуса и там вступает в резонанс со стенками, что в результате приводит к его усилению. По этой причине качество звучания той же гитары сильно зависит от того материала, из которого она сделана и даже от лака которым она покрыта.
- Электрический резонанс – представляет собой совпадение частоты колебаний внешнего напряжения с частотой колебаний электрической цепи, по которой идет ток.
Помимо этих чисто физических резонансов есть еще уже упомянутый нами общественный резонанс – яркий отклик общества на какое-то событие (обычно политическое или экономическое), например брекзит Британии, ее выход из Европейского союза вызвал широкий общественный резонанс во многих странах Европы и особенно, разумеется, в самой Британии.
Есть также и когнитивный резонанс – это полное совпадение во взглядах и мнениях. Например, вы познакомились с новым человеком, а он думает так же как вы, у вас абсолютно схожие взгляды, вкусы, предпочтения, тогда имеет место когнитивный резонанс. И противоположное явление – когнитивный диссонанс, когда вы абсолютно не согласны с кем-то или чем-то, абсолютно не принимаете происходящего. (Например, автор этой статьи, оказавшись в каком-нибудь украинском бюрократическом учреждении, будь-то Жеке, БТИ или налоговой испытывает настоящий когнитивный диссонанс)).