The crystal oscillator is an important electronic component that provides very accurate clock frequency generation at a fraction of the cost.
Due to the piezoelectric effect, its electrical properties change during vibration. Because it is possible to make a crystal that vibrates at a specific frequency, crystal oscillators are very useful for a variety of applications. They appeared in the 1920s, and at first provided precise wave generation for radio stations. In 1970, a revolution in wristwatches occurred when they began to use high-precision quartz oscillators. Computers from the ENIAC of the 1940s to the present day use crystal oscillators to generate clock frequencies. Modern PCs still use crystal oscillators, but more sophisticated technologies are used to achieve multi-gigahertz clock speeds. The PC uses a crystal with a frequency much lower than the operating frequency and multiplies it using phase-locked loop. Computers often use a 14318 crystal because that frequency was used in older televisions and such crystals were inexpensive and widely available. In order for the crystal to vibrate, its circuitry requires additional components. In the 1970s, modular crystal oscillators gained popularity - these compact and easy-to-use microassemblies combined the crystal itself, ICs and discrete components. I became interested in how one of these modules worked, so I opened one of them and reverse engineered its chip. In this post I'll explain how it works and describe the tiny CMOS circuit that controls it. It turned out that there was more interesting stuff going on inside the module than one might have expected.
Generator module
I was studying a module from a card for the IBM PC.
The module is housed in a rectangular metal case with 4 pins that protects the electronics from electrical noise (that's the Rasco Plus in the rectangular case on the right in the photo, not the square IC from IBM). The module generates a signal at 4.7174 MHz, as follows from the inscription on its body. Why does the card use a crystal with such an unusual frequency - 4.7174 MHz? In the 1970s, the IBM 3270 was a very popular CRT terminal. The terminals were connected by coaxial cable and used the Interface Display System Standard protocol, operating at a clock frequency of 2.3587 MHz. In the late 1980s, IBM produced interface cards to connect the IBM PC to the 3270 network. My crystal is from one of these cards (type 56X4927), and the frequency of the crystal is 4.7174 MHz - exactly twice as high as 2.3587 MHz.
The crystal oscillator module is located at the bottom right. Inscription on the case: Rasco Plus. 4.7174 MHZ, Motorola 1987. The square module on the left is an IC from IBM.
I opened the module case to look at its hybrid circuit. I expected to see a quartz crystal there, like a gemstone in a box, but I discovered that quartz oscillators use a very thin quartz disk. I damaged it when opening it, so it's missing a piece at the top right. It is visible on the left side of the photo - metal electrodes approach it on both sides. These, in turn, are connected to small pins on which the crystal is raised above the surface of the housing so that it can vibrate freely.
Inside the crystal oscillator housing are components mounted on a ceramic substrate. They are connected to the circuit with tiny gold bonding wire. A 3 nF capacitor and a 10 ohm film resistor, located on the substrate using a surface mount method, filter out noise coming from the power pin.
HOW TO ORDER A QUARTZ RESONATOR WITH THE REQUIRED CHARACTERISTICS?
Selection from stock:
The warehouse of the COMPEL company supports a wide range of quartz resonators and generators of various series for various frequencies with standard values of frequency instability and load capacitance (Cl).
By typing in the search box on the website www.compel.ru (upper right corner of the page) the name of the quartz resonator series you are interested in, you will see a list of all its components that are currently supported in stock.
Example: KX-KT 13.56 MHz
Delivery to order:
If a component of the required series with the required frequency values and its deviation, load capacity and operating temperature range is not in stock, make and send a request to your manager, using the examples below:
- An example of a request for a KX-9A series quartz resonator at a standard frequency of 25 MHz with a standard deviation of ±30 ppm, a standard load capacitance of 16pF and an operating temperature range of -20...70°C: KX-9A 25.0 MHz;
- An example of a request for a KX-9A series quartz resonator for a non-standard frequency of 26.3 MHz with a non-standard deviation of ±10 ppm, with a non-standard load capacitance of 12 pF and an operating temperature range of -40...85 ° C: KX-9AT 26.3 MHz 12pF 10 ppm.
Detailed information about Geyer Electronic products can be found on the website: https://www.geyer-electronic.com/ in the Frequency Control Products section.
Rice. 3. Appearance of some series of crystal resonators, crystal oscillators and ceramic surface mount resonators of Geyer Electronic
For technical information, ordering samples and delivery, please contact COMPEL. E-mail
New series of quartz resonators
Geyer Electronic has announced the launch of a new series of quartz resonators in CMD packages KX-8 . The dimensions of the products are 4.0x2.5 mm, and the height is 0.8 mm. Frequency range from 12 to 60 MHz with a tolerance from ±10 ppm to ±50 ppm at temperatures from -20 to 70C°. Allowable load capacitance is from 10 to 16 pF. Resonators are also available for extended temperature ranges and are specified for fusion soldering. Resonators will find application in the field of telecommunications and wireless communications.
•••
IC operation diagram
The photo below shows a tiny IC crystal under a microscope. Contact pads and main functional blocks are marked. The green-brown areas are the silicon that forms the IC. A yellowish metallic layer connects the components to the IC. Beneath the metal is a reddish layer of polysilicon where transistors are formed - but it is almost completely covered by the metal layer. Along the edges of the chip there is a welding wire connected to the contact pads connecting the chip to the rest of the module. Two pads (select and disable) are not connected. The chip was manufactured by Motorola in 1986. I did not find any information on the article number SC380003.
IC crystal with markings of main blocks. "FF" stands for triggers. “sel” – contact pads. “cap” – pads connected to internal capacitors
.
IS has two tasks. First, its analog components cause the crystal to vibrate. Second, its digital components divide the frequency by 1, 2, 4, or 8, and produce a high-current clock signal (the divider is set by two selector pins on the IC).
The quartz oscillator is implemented according to the circuit below, which is called the “Colpitts oscillator”. It is more complex than a conventional crystal oscillator circuit. The bottom line is that the crystal and two capacitors oscillate at a given frequency. However, the oscillations would quickly die out if not for the supporting feedback from the supporting transistor.
A typical crystal oscillator is built using a simple circuit called a “Pierce oscillator”, in which a feedback circuit is formed from a crystal and an inverter. The two grounded capacitors in the middle make it very similar to a classic Colpitts oscillator.
I'm not sure why the crystal oscillator I disassembled uses a more complex circuit that requires a tricky voltage bias.
In 1918, Edwin Colpitz, chief researcher at Western Electric, invented an inductor-capacitor crystal oscillator. Today this circuit is known as a Colpitts generator. The idea is that the inductor and capacitor form a “resonant tank” that oscillates at a frequency depending on the characteristics of the components. You can imagine that the electricity in this reservoir seems to splash back and forth between the inductor and the capacitors. The oscillations themselves would quickly die out, so an amplifier is used to feed them. In the original Colpitts oscillator, the amplifier was a vacuum tube. Later circuits switched to transistors, but this amplifier may be an operational amplifier or another type. In other circuits, the end is grounded so that there is feedback in the middle. Then the capacitors do not invert anything, so a non-inverting amplifier is used.
Simplified diagram of a Colpitts generator with basic components.
The key feature of the Colpitts generator is the two capacitors that form the voltage divider. Since they are grounded in the middle, they will have opposite voltages at the two ends: when one goes up, the other goes down. The amplifier takes the signal from one end, amplifies it, and sends it to the other. The amplifier inverts the signal, and the capacitors provide a second inversion, so that the feedback amplifies the original signal (providing a 360° phase shift).
In 1923, George Washington Pierce, a professor of physics at Harvard, replaced the inductor in the Colpitts generator with a crystal. Thanks to this, the generator became more accurate, and it began to be widely used in radio transmitters and other devices. Pierce patented his invention and made decent money from companies such as RCA and AT&T. The presence of patents led to many years of litigation, which eventually reached the Supreme Court.
For several decades, the Pierce generator was commonly called a Colpitts generator with a crystal. The Pierce generator often lacked the characteristic capacitors, instead using the stray capacitance of a vacuum tube. The terminology gradually changed, and the two different types of crystal oscillators began to be called the Colpitts oscillator (with capacitors) and the Pierce oscillator (without them).
Another change in terminology occurred due to the fact that the Colpitts oscillator, Pierce oscillator, and Clapp oscillator were topologically identical crystal oscillators, differing only in which part of the circuit was considered to be ground (collector, emitter, or base, respectively). All these oscillators can be called Colpitts oscillators, only with a common collector, common emitter or common base.
I made this excursion into history in order to show that in various sources these generators are called differently, Colpitts or Pierce generators, and in a contradictory way. The generator that I studied can be called a Colpitts generator with a common drain (by analogy with a common collector). It can also be called a Colpitts generator based on the grounding arrangement. But historically it can be called a Peirce oscillator because it uses a crystal. It is also called a single terminal crystal oscillator because only one terminal of the crystal is connected to the external circuit (the other is grounded).
Simplified generator circuit
Increasing the voltage on the crystal turns on the transistor, current flows into the capacitors, increasing the voltage across them (and on the crystal). Reducing the voltage on the crystal turns off the transistor, the current drain (circle with arrow) draws current from the capacitors, reducing the voltage on the crystal. Thus, feedback from the transistor amplifies the oscillations of the crystal, maintaining them.
Bias voltage and current circuits are an important part of this circuit. The bias voltage sets the transistor's gate somewhere between on and off, so voltage fluctuations across the chip turn it on and off. The bias current is halfway between the transistor's on and off currents, so the current flowing into and out of the capacitors is balanced (I'm simplifying by talking about on and off states - in reality the signal will be a sine wave).
Bias voltage and current circuits are moderately complex analog circuits consisting of a bunch of transistors and a few resistors. I will not describe them in detail, I will only say that they use feedback circuits to generate the required fixed values of voltage and current.
A significant part of the IC is occupied by five capacitors. In the diagram, one is located at the top, three run in parallel to form the bottom capacitor in the circuit, and one stabilizes the bias voltage circuit. The photo of the crystal below shows one of the capacitors after the top metal layer has been dissolved. The red and green areas are the polysilicon that forms the top plate of the capacitor along with the metal layer. The pinkish area located under the polysilicon is probably silicon nitride, which forms the dielectric layer. Doped silicon, which is not visible in the photo, forms the bottom plate of the capacitor.
Capacitor on chip. The large pale square on the left is the pad for connecting the bonded wire to the IC. The complex structures on the left are the clamping contact diodes. The clover-like structures on the right are transistors.
Interestingly, the capacitors on the chip are not connected together. They are connected to three platforms connected to each other by welding wire. Perhaps this gives the circuit flexibility - the circuit's capacitance can be changed by removing the conductor leading to the capacitor.
GEYER ELECTRONIC QUARTZ RESONATORS
To correctly select a quartz resonator, you need to know the main important parameters of its equivalent circuit, which, together with the basic formulas, is shown in Figure 1.
Rice. 1. Equivalent circuit of a quartz resonator and basic formulas important for practice, illustrating the relationship of the main parameters
As can be seen from the diagram in Figure 1, due to the presence of capacitance C1, the resonator has a series resonance frequency fS, and due to capacitance C0, it has a parallel resonance frequency fP. The values of L1 and C1 depend on the mechanical properties of the quartz plate, and the resistance R1 characterizes the damping of mechanical vibrations. The value of capacitance C0 is determined by the electrodes of the resonator and the capacitance of the supply wires. It is clear from the formulas that the frequency of series resonance depends only on strictly defined parameters of the resonator L1 and C1, and the frequency of parallel resonance varies from a much less certain value of the interelectrode capacitance C0. The most important parameter of a quartz resonator is the quality factor Q (it is called “Q” from the first letter “Quality factor” or quality factor). From the point of view of electrical parameters, a quartz resonator behaves like an oscillating circuit with a high quality factor. The frequency stability of LC oscillators is insufficient in most practical cases. With the help of quartz resonators, practically achievable values of frequency instability Df/f are in the range from 10...6 to 10...10.
It often becomes necessary to adjust the frequency of a quartz resonator within small limits to achieve the required frequency value. To do this, a control capacitance CL is connected in series with the quartz resonator, the capacitance of which is large compared to C1 (see Figure 2).
Rice. 2. Illustration of the effect of capacitance CL on resonant frequencies
When capacitance CL is connected in series, only the frequency of the series resonance changes. When a capacitor CL is connected in parallel, only the parallel resonance frequency changes its value (see the top of Figure 1). A crystal resonator is always part of the oscillator circuit. By itself, without an amplifier in a self-oscillator switched on, quartz is of little interest. This means that the generated frequency is affected not only by the parameters of the resonator, but also by the input circuit of the amplifier. Knowing the equivalent capacitance of the amplifier, which, in fact, is the capacitance CL, you can accurately calculate the frequency at the output of the quartz oscillator. That is why, when choosing a quartz resonator, it is necessary to pay attention to the value of the load capacitance CL, indicated by the manufacturer in the technical documentation. Examples of graphs showing the magnitude of the influence of the load capacitance CL on the range of changes in the resonant frequency are shown in the lower part of Figure 2. It is clearly seen that the greater the value of CL, the smaller the range of changes in frequency near this capacitance value. Of course, for a more accurate calculation it is necessary to take into account the value of capacitance C0.
To generate frequencies above 35...40 MHz, oscillations of the third, fifth, seventh and higher harmonics of quartz resonators are often used. This information is usually noted in the manufacturer's documentation. For frequencies generated at harmonics other than the fundamental, the ratio of capacitances C0 and C1 depends on the square of the harmonic number (see formulas at the bottom of Figure 1). Typically, generation at the first harmonic is more stable and stable than at non-fundamental harmonics (the third harmonic is most often used).
Table 1 shows the parameters of the popular series of Geyer Electronic quartz resonators for through-hole mounting, and Table 2 shows the most popular series for surface mounting.
Table 1. Quartz resonators from Geyer Electronic for through-hole mounting
| Series | Range of available frequencies1, (MHz) | Operating temperature range2, (°C) | Frequency instability at 25°С, (ppm) | CL, (pF) | R1, (Ohm) | C0, (pF) | Dimensions, (mm) |
| KX-26 | 32.768 kHz | -20…70 -40…85 | ±30 | 12,5 | 30 kOhm | 1,3 | 2,0×6,2 |
| 77,5 | |||||||
| KX-38 | 32.768 kHz | ±20 | 3,0×8,0 | ||||
| KX-39 | 3,579545…40,0 | ±30 | 16,0 (12…20)3 | 50…150 | 7,0 | 3,0×10,0 | |
| 30,0…70,0 | ±50 | see Datasheet | |||||
| 40,0…100,0 | 12,0 | 40 | 3,0 | ||||
| KX-49 | 1,84320…30,0 | -20…70 -40…85 -40…105 | ±30 (±5…50)3 | 30,0 (10…30)3 | 60…600 | 7,0 | 11,3/4,9/ 13,6 |
| 20,0…90,0 | see Datasheet | 30…60 | |||||
| 50,0…150,0 | 40…70 | ||||||
| 110,0…200,0 | 80…120 | ||||||
| KX-3H | 3,20…70,0 | ±30 (±10…50)3 | 16,0 (12…20)3 | 50…150 | 11,35/5,0/ 3,5 |
1 The range of available frequencies includes a grid of standard (most common) frequency values. Most quartz crystals for these frequencies are always kept in stock, and if not available, they are promptly supplied from the Geyer Electronics warehouse. Quartz resonators for unique frequencies not included in the standard grid are also available, but have a longer delivery time. 2 Geyer Electronics quartz resonators are available in temperature ranges suitable for commercial, industrial or automotive (not all series) applications. When ordering a quartz resonator, this is taken into account by adding the appropriate letters after the series name. For example, for the range -20...70°С nothing is added to the series name, for the range -40...85°С "T" is added, and for -40...105 "E" is added. Example: KX-49, KX-49T, KX-49E respectively. Geyer Electronics quartz resonators are available in temperature ranges suitable for commercial, industrial or automotive (not all series) applications. When ordering a quartz resonator, this is taken into account by adding the appropriate letters after the series name. For example, for the range -20...70°С nothing is added to the series name, for the range -40...85°С "T" is added, and for -40...105 "E" is added. Example: KX-49, KX-49T, KX-49E respectively. 3 The table shows the standard values of the load capacitance of a quartz resonator. Capacities in parentheses are available on request.
Table 2. Quartz resonators from Geyer Electronic for surface mounting
| Series | Range of available frequencies1, (MHz) | Operating temperature range2, (°C) | Frequency instability at 25°C, (ppm) | CL, pF | R1, (Ohm) | C0, (pF) | Dimensions, (mm) |
| KX-327S | 32.768 kHz | -20…70 (-40…85) | ±30 | 12,5 | 50 | 2,0 | 8,7/3,8/ 2,5 |
| KX-327L | ±20 | 12,5 | 65 | 0,8 | 7,0/1,5/ 1,4 | ||
| KX-327NT | -40…85 | ±30 (±20) | 12,5 (7…9)3 | 50 | 2,0 | 3,2/1,2/ 0,95 | |
| KX-327XS | -20…70 (-40…85) | 12,5 (6…12,5)3 | 65 | 2,0 | 4,95/1,82/ 0,96 | ||
| KX-K | 3,5…70,0 | -20…70 (-40…85) | ±30 | 16 (12…30)3 | 50…150 | 7,0 | 12,3/4,5/ 5,0 |
| KX-KS | 12,3/4,5/ 3,2 | ||||||
| KX-MC | 3,5…60,0 | -20…70 -40…85 -40…105 | ±50 | 16 (12…20)3 | 13,0/4,7/ 4,1 | ||
| KX-CPB | 3,5…70,0 | -20…70 (-40…85) | 50…120 | 13,0/4,73/ 4,3 | |||
| KX-CPBS | 13,0/4,73/ 3,8 | ||||||
| KX-20 | 3,579545… 25,0 | -20…70 -40…85 -40…105 | 50…150 | 11,6/5,5/ 1,6 | |||
| KX-13 | 6,0…160,0 | ±30 | 30…120 | 7,0/5,0/ 1,3 | |||
| KX-12A | 8,0…150 | ±50 | 16 (10…20)3 | 40…100 | 5,0 | 6,0/3,5/ 1,1 | |
| KX-12B | 8,0…50,0 | ±30 | 40…80 | 7,0 | 6,5/3,5/ 1,2 | ||
| KX-9A | 8,0…300,0 | ±30 (±10…±50)3 | 30…100 | 5,0 | 5,0/3,2/ 0,85 | ||
| KX-9B | 8,0…50,0 | ±30 | 10…20 | 40…100 | 5,0/3,2/ 1,0 | ||
| KX-8 | 12,0…60,0 | ±30 (±10…±50)3 | 16 (10…20)3 | 50…80 | 4,0/2,5/ 0,8 | ||
| KX-7 | 12,0…60,0 | 16 (7…20)3 | 50…100 | 3,2/2,5/ 0,7 | |||
| KX-6 | 16,0…80,0 | 10 (8…16)3 | 50…120 | 2,5/2,0/ 0,55 | |||
| KX-5 | 20,0…80,0 | -20…70 (-40…85) | 8 (8…16)3 | 80…100 | 2,0/1,6/ 0,55 |
1, 2, 3 - see footnotes for table 1.
Digital circuit
On the right side of the chip is a digital circuit that divides the crystal's output frequency by 1, 2, 4, or 8. Thanks to it, the same crystal can output four frequencies. The divider is made up of three flip-flops connected in series. Each divides the incoming pulse in half. A 4 to 1 multiplexer selects between the original pulse frequency or the output from one of the flip-flops. Selection is accomplished using wires that connect to two selection pads on the right side of the chip. The final frequency is fixed at the production stage. Four NAND gates along with inverters are used to decode the pins and generate four control signals to the multiplexer and flip-flops.
Solid modules
Many of the points described above can be omitted when using ready-made generator modules. These modules already include everything necessary to generate a clock frequency, have a low-impedance output and an output signal shape - square wave ( note : there is also a sine wave, square wave is the most common option). Crystal oscillators and silicon oscillators are the most common. Crystal oscillators have similar accuracy if assembled using discrete components and a quartz resonator. Silicon oscillator modules have higher accuracy than those assembled from discrete components, and can even have accuracy comparable to ceramic resonator oscillators.
Implementation of CMOS logic
The chip is built on CMOS (complementary metal-oxide-semiconductor) logic. It uses two types of transistors, N-MOS and P-MOS, working together. The diagram below shows the design of an N-MOS transistor. A transistor can be thought of as a switch between source and drain that controls a gate. The source and drain (green) consist of sections of silicon with additives that change its semiconductor properties - N+ silicon. The valve is made of a special silicon, polysilicon, separated from the silicon substrate by a very thin insulating layer of oxide layer. The N-MOS transistor turns on when the valve is pulled up.
Structure of an N-MOS transistor. The structure of the P-MOS transistor is similar, but the N- and P-type silicon sections are swapped.
The structure of a P-MOS transistor is the opposite of an N-MOS: the source and drain consist of P+ silicon embedded in N silicon. It also works opposite to the N-MOS transistor: it turns on when the valve is pulled down. Typically, P-MOS transistors pull the drain up and N-MOS transistors pull down. In CMOS, transistors work to complement each other, pulling the output signal up or down as needed.
The diagram below shows how a NAND gate is implemented in CMOS. If a 0 is applied to the input, the corresponding P-MOS transistor (top) will turn on and pull the output up. If both inputs are 1, the NMOSFET (bottom) will turn on and pull the output down. Thus, the circuit implements the NAND function.
The diagram below shows what a NAND gate looks like on a die. Unlike textbook images, real transistors have complex, curved shapes. On the left side there is a P-MOS transistor, and on the right there is an N-MOS transistor. The reddish traces above the silicon are the polysilicon that forms the gates. Most of the silicon in the substrate is conductive due to additives, and appears slightly darker than non-conducting silicon without additives on the left and right edges, as well as in the center. To make this photo, the metal layer was etched away. The yellow lines indicate where metal conductors used to be. The circles are connections between the metal layer and the underlying layers, silicon or polysilicon.
What a NAND gate looks like on a chip
The transistor in the photo can be compared with the NAND gate circuit. Look at the polysilicon formed transistor gates, and what they share. From section +5 there is a path to the output through the long P-MOS transistor on the left. The second path is through the small P-MOS transistor in the center - this shows that the transistors are connected in parallel. Each gate controls one of the inputs. On the left, the path from ground to the output should go through both concentric N-MOS transistors - they are connected in series.
This IC also uses many ring gate transistors. This unusual element arrangement technique makes it possible to place many parallel transistors at a high density. The photo below shows 16 ring gate transistors. The copper-colored clover-like patterns are the drain of the transistors, and on the outside is the source. The metal layer (here it is removed) combines all sources, valves and drains, respectively. Parallel transistors work like one big one. Parallel transistors are used to supply high currents to the output. In a bias circuit, different numbers of transistors (6, 16, or 40) are connected together to produce the desired current ratio.
Generator frequency stability
The oscillator is expected to maintain its frequency for a longer period of time without any changes in order to have a smoother pure sine wave output for the circuit to operate. Therefore, the term "frequency stability" does have a lot of meaning when it comes to generators, be they sine wave or non-sine wave.
Generator frequency stability is defined as the ability of a generator to maintain the required frequency as constant over a long period of time as possible. Let's try to discuss the factors influencing this frequency stability.
Change in operating point
We have already become acquainted with the parameters of the transistor and learned how important the operating point is. The stability of this operating point for the transistor used in the amplification circuit (BJT or FET) is of greater importance.
The operation of the active device used is adjusted to correspond to the linear part of its characteristics. This point shifts due to temperature fluctuations and hence stability is affected.
Temperature change
The tank circuit in the generator circuit contains various frequency determining components such as resistors, capacitors and inductors. All their parameters depend on temperature. Due to temperature changes, their values are affected. This leads to a change in the frequency of the generator circuit.
Due to nutrition
Changes in power supply also affect frequency. Changes in the power supply result in changes in Vcc. This will affect the frequency of vibrations produced.
To avoid this, a regulated energy supply system has been introduced. This is called RPS in short. The details of regulated power supply have been clearly discussed in the power supply section of the electronic circuits tutorial.
Changing Output Load
Changes in output impedance or output load also affect the generator frequency. When a load is connected, the effective resistance of the tank circuit changes. As a result, the LC quality factor of the tuned circuit changes. This leads to a change in the output frequency of the generator.
Changes in intercell capacitances
Intercell capacitances are capacitances that develop in PN junction materials such as diodes and transistors. They are designed because of the charge present in them during their operation.
Inter-element capacitors undergo changes due to various reasons such as temperature, voltage, etc. This problem can be solved by connecting a damping capacitor across the faulty inter-element capacitor.
Transfer valve
Another key circuit of the chip is the transfer gate. It works like a switch through which the signal either passes through or does not. The diagram below shows how a transfer gate is made from two transistors, an N-MOS transistor and a P-MOS transistor. If a high voltage is applied to the enable line, both transistors turn on and the input signal passes to the output. If the voltage is low, they turn off, blocking the signal. The symbol of the transfer valve in the diagrams is shown on the right.
Consumption current
Current consumption is another important point in choosing a clock source. The power consumed by a discrete component generator is largely determined by the amplifier's current consumption and its load capacitance. The current consumption of CMOS amplifiers directly depends on the operating frequency and power dissipation per load capacitance. For example, the load capacitance for a standard HC04 logic inverter is usually around 90 pF. When operating at a frequency of 4 MHz and a supply voltage of 5 V, the current consumption will be about 1.8 mA. The quartz resonator also has a certain capacitance, on average about 20 pF, and the current consumption, taking into account this load, will already be about 2.2 mA.
A ceramic resonator usually implies a higher load capacitance compared to a crystal resonator and therefore the current consumption will be higher using the same amplifier in both cases.
In comparison, quartz-based modules typically have a current consumption of 10 mA to 60 mA because they have built-in temperature compensation and module control circuitry.
Current consumption for silicon oscillators depends on their type and can range from a few microamps (low-frequency oscillators) to tens of milliamps (programmable oscillators). For example, a cost-effective silicon oscillator like the MAX7375 has a current consumption of less than 2 mA with an output frequency of 4 MHz.
Multiplexer
A multiplexer is used to select one of four clock signals. The diagram below shows how a multiplexer is implemented using transfer gates. The multiplexer accepts four input signals: A, B, C and D. One of the inputs is selected by activating the corresponding selection line and its addition. This input is connected through a transfer valve to the output, and other inputs are blocked. Although a multiplexer can be built using standard logic gates, its implementation using transfer gates is more efficient.
The diagram below shows the transistors that make up the multiplexer. A pair of transistors is connected to inputs B and C. I think this was done because a pair of transistors have half the resistance. Since inputs B and C are designed for high frequency signals, the transistor pair reduces delay and distortion.
The photo below shows how the multiplexer is physically implemented on the chip. The polysilicon valves are best seen. The metal layer has been removed. Metal conductors ran vertically, connecting the corresponding segments of the transistors. The sources and drains of neighboring transistors are combined into single sections located between the valves. The upper rectangle contains N-MOS transistors, and the lower rectangle contains P-MOS transistors. Since P-MOS transistors are less efficient, the bottom rectangle needs to be larger.
Crystal oscillators
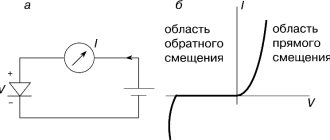
The operating principle of crystal oscillators depends on the piezoelectric effect
. The natural shape of the crystal is hexagonal. When a crystal wafer is bent perpendicular to the X-axis, it is called an X-cut, and when it is cut along the Y-axis, it is called a Y-cut.
The crystal used in a crystal oscillator has a property called piezoelectric property. So let's understand the piezoelectric effect.
Piezoelectric effect
A crystal exhibits the property that when mechanical stress is applied to one of the crystal faces, a potential difference develops on the opposite faces of the crystal. Conversely, when a potential difference is applied to one of the faces, mechanical stress is created along the other faces. This is known as the piezoelectric effect
.
Some crystalline materials, such as Rochelle salt, quartz and tourmaline, have a piezoelectric effect, and such materials are called piezoelectric crystals
. Quartz is the most commonly used piezoelectric crystal because it is inexpensive and readily available in nature.
When a piezoelectric crystal is exposed to an alternating potential, it vibrates mechanically. The amplitude of mechanical vibrations becomes maximum when the frequency of the alternating voltage is equal to the natural frequency of the crystal.
Trigger
There are three flip-flops on the chip that divide the clock frequency.
A crystal oscillator uses switched flip-flops that switch between 0 and 1 every time it receives an incoming pulse. Since two incoming pulses produce one outgoing pulse (0→1→0), the flip-flop divides the frequency in half. The flip-flop consists of transfer gates, inverters and a NAND gate - see the diagram below. When the input clock signal is 1, the output passes through the inverter and the first transfer gate to point A. When the input signal switches to 0, the first transfer gate opens, and point A remains at the previous value. Meanwhile, the second transfer gate closes, so the signal passes through the second inverter and transfer gate to point B. The NAND gate inverts it again, causing the output value to reverse. A second cycle of the incoming clock signal repeats this process, causing the output to return to its original value. As a result, two cycles of input signals produce one cycle of output signal, so the flip-flop divides the frequency by 2.
Each flip-flop has an enable input. If the trigger for the selected output is not needed, it is disabled. For example, if divide by 2 mode is selected, only the first trigger is used and the other two are disabled. I believe this is done to reduce power consumption. This is independent of the trip contact on the module, which completely blocks the output signal. This disabled property is optional; This module does not have such a function and the trip contact is not connected to the IC.
In the diagram above, the inverters and transfer valves are shown as separate structures. However, the flip-flop uses an interesting gate structure, combining an inverter and a transfer gate (left) into a single gate (right). A pair of transistors connected to data in act as an inverter. However, if the clock signal is zero, power and ground are blocked and the gate has no effect on the output, maintaining the previous voltage. This is how a transfer valve works.
Combination inverter and transfer gate
The photo below shows how one of these gates is implemented on a chip. The photo shows the metal layer on top. Below it you can see reddish polysilicon valves. On the left are two P-MOS transistors in the form of concentric circles. On the right are the N-MOS transistors.
What is it and why is it needed
The device is a source that provides high-precision harmonic oscillations. Compared with analogues, it has greater operating efficiency and stable parameters.
The first examples of modern devices appeared on radio stations in 1920-1930. as elements that have stable operation and are capable of setting the carrier frequency. They:
- replaced crystal resonators operating on Rochelle salt, which appeared in 1917 as a result of the invention of Alexander M. Nicholson and were characterized by instability;
- replaced the previously used circuit with a coil and a capacitor, which did not have a high quality factor (up to 300) and depended on temperature changes.
A little later, quartz resonators became an integral part of timers and clocks. Electronic components with a natural resonant frequency of 32768 Hz, which in a binary 15-bit counter sets a time period equal to 1 second.
The devices are used today in:
- quartz watches, ensuring their accuracy regardless of ambient temperature;
- measuring instruments, guaranteeing them high accuracy of indicators;
- marine echo sounders, which are used in research and creation of bottom maps, recording reefs, shoals, and searching for objects in the water;
- circuits corresponding to reference oscillators that synthesize frequencies;
- circuits used in wave indication of SSB or telegraph signal;
- radio stations with DSB signal with intermediate frequency;
- bandpass filters of superheterodyne receivers, which are more stable and high-quality than LC filters.
The devices are manufactured with different housings. They are divided into output ones, used in volumetric mounting, and SMD, used in surface mounting.