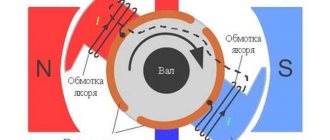
External speed characteristic (VSCH)
The external speed characteristic of the engine shows the dependence of power, fuel consumption and torque on the crankshaft speed. All these parameters are shown graphically in the form of curves.
External speed characteristic
In the figure you can see curves with the designations Pe - engine power, Me - torque, ge - specific fuel consumption. As you can see, with increasing speed and power, fuel consumption increases. The torque increases to a certain level and then decreases. At the point where the engine torque and power are most efficient, there will be the most optimal fuel consumption.
Motor manufacturers are fighting to ensure that the engine develops maximum torque in the widest possible speed range (“the torque plateau is wider”), and maximum power is achieved at speeds as close as possible to this shelf. Such an engine will pull you out of the swamp and allow you to accelerate quickly in the city.
The external speed characteristic evaluates the dynamic characteristics of the car, determines efficiency and fuel consumption for different parameters.
High torque at lower speeds increases the unit's traction force, load capacity and maneuverability.
Basic parameters of the electric motor
Motor power
Motor power is the useful mechanical power at the motor shaft.
Mechanical power
Power is a physical quantity that shows how much work a mechanism does per unit of time.
- where P
– power,
W
, - A
– work,
J
, - t
—time,
s
Work is a scalar physical quantity equal to the product of the projection of force and direction F
and the path
s
traversed by the point of application of the force.
- where s
– distance,
m
For rotational movement
- where θ – angle, rad
- where ω – angular frequency, rad/s
,
In this way, you can calculate the value of mechanical power on the shaft of a rotating electric motor
Rotation frequency
- where n
is the rotation speed of the electric motor,
rpm
Rotor moment of inertia
The moment of inertia is a scalar physical quantity, which is a measure of the inertia of a body in rotational motion around an axis, equal to the sum of the products of the masses of material points by the squares of their distances from the axis
- where J
is the moment of inertia,
kg∙m 2
, - m
—mass,
kg
1 oz∙in∙s 2 = 0.007062 kg∙m 2 (kg∙m 2)
The moment of inertia is related to the moment of force by the following relation
- where ε – angular acceleration, s -2
Electric motor efficiency
The efficiency of an electric motor is a characteristic of the machine’s efficiency in converting electrical energy into mechanical energy.
- where η is the efficiency of the electric motor,
- P1
- supplied power (electric),
W
, - P2
- useful power (mechanical),
W
- Wherein
losses in electric motors
- due to:
- electrical losses - in the form of heat as a result of heating current-carrying conductors;
- magnetic losses - losses due to magnetization reversal of the core: losses due to eddy currents, hysteresis and magnetic aftereffects;
- mechanical losses - friction losses in bearings, ventilation, brushes (if any);
- additional losses - losses caused by higher harmonics of magnetic fields arising due to the gear structure of the stator, rotor and the presence of higher harmonics of the magnetomotive force of the windings.
Application areas of electric motors
Electric motors are the largest consumers of electricity in the world, accounting for about 45% of all electricity consumed.
- Electric motors are used everywhere, the main areas of application are:
- industry: pumps, fans, compressors, conveyors, driving force for other machines, etc.
- construction: pumps, fans, conveyors, elevators, heating, ventilation and air conditioning systems, etc.
- consumer devices: refrigerators, air conditioners, personal computers and laptops (hard drives, fans), vacuum cleaners, washing machines, mixers, etc.
Transition from angular to linear velocity
There is a difference between the linear velocity of a point and the angular velocity. When comparing the quantities in the expressions describing the rules of rotation, you can see the commonality between these two concepts. Any point B belonging to a circle with radius R makes a path equal to 2*π*R. At the same time, it makes one revolution. Considering that the time required for this is the period T, the modular value of the linear velocity of point B is found by the following action:
ν = 2*π*R / Т = 2*π*R* ν.
Since ω = 2*π*ν, it turns out:
Consequently, the linear speed of point B is greater, the further away the point is from the center of rotation.
For your information. If we consider cities at the latitude of St. Petersburg as such a point, their linear speed relative to the earth’s axis is 233 m/s. For objects on the equator – 465 m/s.
The numerical value of the acceleration vector of point B, moving uniformly, is expressed through R and angular velocity, thus:
a = ν2/ R, substituting here ν = ω* R, we get: a = ν2/ R = ω2* R.
This means that the larger the radius of the circle along which point B moves, the greater the value of its acceleration in absolute value. The farther a point of a rigid body is located from the axis of rotation, the greater the acceleration it has.
Therefore, it is possible to calculate accelerations, velocity modules of the required points of bodies and their positions at any time.
Understanding and ability to use calculations and not get confused in definitions will help in practice to calculate linear and angular velocities, as well as freely move from one quantity to another when making calculations.