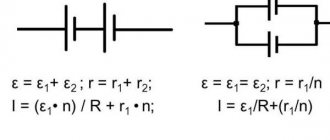Номинальная частота вращения — частота вращения, соответствующая работе машины при номинальных напряжении, мощности и частоте тока и номинальных условиях применения.

Внешняя скоростная характеристика (ВСХ)

Внешняя скоростная характеристика двигателя показывает зависимость мощности, расхода топлива и крутящего момента от числа оборотов коленвала. Все эти параметры показываются графически в виде кривых.

На рисунке можно видеть кривые с обозначениями Pe – мощность двигателя, Mе – крутящий момент, ge – удельный расход топлива. Как видно, с ростом числа оборотов и мощности увеличивается расход топлива. Крутящий момент растет до определенного уровня, а затем идет на спад. В точке, где наиболее эффективный крутящий момент и мощность двигателя, будет самый оптимальный показатель расхода топлива.

Производители моторов борются за то, чтобы максимальный крутящий момент двигатель развивал в как можно более широком диапазоне оборотов («полка крутящего момента была шире»), а максимальная мощность достигалась при оборотах, максимально приближенных к этой полке. Такой двигатель и из болота вытянет, и в городе позволяет быстро ускоряться.

Внешняя скоростная характеристика дает оценку динамическим характеристикам автомобиля, определяет КПД и топливный расход при разных параметрах.

Высокий крутящий момент на более низких оборотах увеличивает тяговую силу агрегата, грузоподъемность и проходимость.

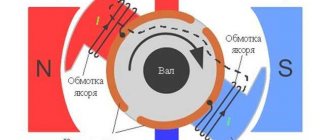
Основные параметры электродвигателя

Мощность электродвигателя

Мощность электродвигателя — это полезная механическая мощность на валу электродвигателя.

Механическая мощность

Мощность — физическая величина, показывающая какую работу механизм совершает в единицу времени.

• где P
  – мощность,
  Вт
  ,
• A
  – работа,
  Дж
  ,
• t
  — время,
  с

Работа — скалярная физическая величина, равная произведению проекции силы на направление F

и пути
s
, проходимого точкой приложения силы.

• где s
  – расстояние,
  м

Для вращательного движения

• где θ – угол, рад

• где ω – углавая частота, рад/с
  ,

Таким образом можно вычислить значение механической мощности на валу вращающегося электродвигателя

Частота вращения

• где n
  — частота вращения электродвигателя,
  об/мин

Момент инерции ротора

Момент инерции — скалярная физическая величина, являющаяся мерой инертности тела во вращательном движении вокруг оси, равна сумме произведений масс материальных точек на квадраты их расстояний от оси

• где J
  – момент инерции,
  кг∙м 2
  ,
• m
  — масса,
  кг

1 oz∙in∙s 2 = 0,007062 kg∙m 2 (кг∙м 2 )

Момент инерции связан с моментом силы следующим соотношением

• где ε – угловое ускорение, с -2

Коэффициент полезного действия электродвигателя

Коэффициент полезного действия (КПД) электродвигателя — характеристика эффективности машины в отношении преобразования электрической энергии в механическую.

• где η – коэффициент полезного действия электродвигателя,
• P1
  — подведенная мощность (электрическая),
  Вт
  ,
• P2
  — полезная мощность (механическая),
  Вт

При этом

потери в электродвигатели

обусловлены:
• электрическими потерями — в виде тепла в результате нагрева проводников с током;
• магнитными потерями — потери на перемагничивание сердечника: потери на вихревые токи, на гистерезис и на магнитное последействие;
• механическими потерями — потери на трение в подшипниках, на вентиляцию, на щетках (при их наличии);
• дополнительными потерями — потери вызванные высшими гармониками магнитных полей, возникающих из-за зубчатого строения статора, ротора и наличия высших гармоник магнитодвижущей силы обмоток.

Области применения электродвигателей

Электродвигатели являются крупнейшими потребителями электроэнергии в мире, на них приходится около 45% от всей потребляемой электроэнергии.

Электродвигатели используются повсеместно, основные области применения:
• промышленность: насосы, вентиляторы, компрессоры, конвейеры, движущая сила для других машин и др.
• строительство: насосы, вентиляторы, конвейеры, лифты, системы отопления, вентиляции и кондиционирование воздуха и др.
• потребительские устройства: холодильники, кондиционеры, персональные компьютеры и ноутбуки (жесткие диски, вентиляторы), пылесосы, стиральные машинки, миксеры и др.

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

ν = 2*π*R / Т = 2*π*R* ν.

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.