In the course of general physics, Ohm's and Kirchhoff's laws, which include voltages, currents and resistances, are mainly used to calculate electrical circuits. However, to calculate complex electrical circuits, and especially AC circuits, it is advisable to use conductivity instead of resistance.
Conductivity in a DC circuit g is the reciprocal of resistance
The SI unit of conductivity is the siemens (in honor of the 19th century German electrical engineer E.W. Siemens).
1 Sim is the conductivity of a conductor with a resistance of 1 ohm.
In alternating current circuits, as is known, there are three types of resistance: active R, reactive and total g. By analogy with this, three types of conductances have been introduced: active g, reactive b and total y. However, only the admittance y is the reciprocal of the total resistance:
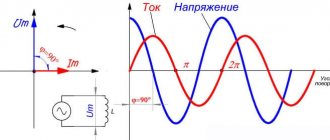
To introduce active g and reactive b conductivities, consider an alternating current circuit of active R and inductive reactances connected in series (Fig. 1-25, a). Let's construct a vector diagram for it (Fig. 1-25, b). We will decompose the current in the circuit into active and reactive components and from the resulting triangle of currents we will move on to the triangle of resistance (Fig. 1-25, c). From the latter we have:
From the vector diagram (see Fig. 1-25, b) taking into account formula (1.30) we have:
where is the active conductivity,
where is the reactivity.
Now let's establish the relationship between conductivities. For the circuit under consideration we have:
Substituting the values from relations (1.31) and (1.32) respectively, we obtain:
where is the total conductance of the circuit.
By analogy with the resistance triangle (Fig. 1-25, c), we build a conductivity triangle (Fig. 1-25, d). By analogy with inductive and capacitive reactance, a distinction is made between inductive and capacitive conductivity.
In the case of a branched circuit (Fig. 1-26, a), the circuit can be easily converted into a so-called equivalent circuit (Fig. 1-26, b), in which two branches are replaced by one with corresponding equivalent active and
reactances. Calculating the latter resistance, as well as other circuit parameters, is easier using conductances. Let us establish the basic laws for conductivity in a branched circuit.
Let us express the total current in terms of its components or equivalent conductivities:
In turn, the active component of the total current is equal to the sum of the active components of the branch currents:
i.e., the equivalent active conductance of the branch is equal to the arithmetic sum of the active conductances of the branches.
Since the reactive components of the branches of the circuit under consideration are in antiphase, then for the reactive component of the total current we have:
i.e., the equivalent reactive conductivity of the branching is equal to the algebraic sum of the reactive conductivities of parallel branches, and is taken with a “plus” sign, and with a “minus” sign.
. Capacitor (ideal capacity)
The processes for an ideal container are similar. Here . Therefore, from (3) it follows that. Thus, no active power is consumed in the inductor and capacitor (P = 0), since irreversible conversion of energy into other types of energy does not occur in them. Here only energy circulation occurs: electrical energy is stored in the magnetic field of a coil or the electric field of a capacitor for a quarter of a period, and over the next quarter of a period the energy is returned to the network. Because of this, the inductor and capacitor are called reactive elements, and their resistances X L and X C, in contrast to the active resistance R of the resistor, are called reactive.
The intensity of energy exchange is usually characterized by the highest value of the rate of energy input into the magnetic field of a coil or the electric field of a capacitor, which is called reactive power
.
In general, the expression for reactive power has the form:
It is positive when the current is lagging (inductive load -) and negative when the current is leading (capacitive load -). The unit of power as applied to the measurement of reactive power is called reactive volt-ampere
(VAR).
In particular, for the inductor we have: , since.
.
From the latter it can be seen that the reactive power for an ideal inductor is proportional to the frequency and the maximum energy reserve in the coil. Similarly, we can obtain for an ideal capacitor:
.
Resistor (ideal active resistance).
Here the voltage and current (see Fig. 2) are in phase, so the power is always positive, i.e. resistor consumes active power
Transient processes in linear electrical circuits. Basic concepts, laws of communication.
With all changes in the electrical circuit: switching on, switching off, short circuit, fluctuations in the value of any parameter, etc. – transient processes occur in it, which cannot occur instantly, since an instantaneous change in the energy stored in the electromagnetic field of the circuit is impossible. Thus, the transient process is caused by a discrepancy between the amount of stored energy in the magnetic field of the coil and the electric field of the capacitor and its value for the new state of the circuit. During transient processes, large overvoltages, overcurrents, and electromagnetic oscillations can occur, which can disrupt the operation of the device until it fails. On the other hand, transient processes find useful practical application, for example, in various types of electronic generators. All this necessitates the study of methods for analyzing non-stationary operating modes of a circuit.
Basic methods for analyzing transient processes in linear circuits:
- Classic method
consisting in the direct integration of differential equations describing the electromagnetic state of the circuit.
Operator method
which consists in solving a system of algebraic equations regarding images of the desired variables, followed by the transition from the found images to the originals.
Frequency method
based on the Fourier transform and widely used in solving synthesis problems.
Calculation method using the Duhamel integral,
used when the disturbance curve has a complex shape.
State variable method,
which is an ordered method for determining the electromagnetic state of a circuit based on solving a system of first-order differential equations written in normal form (Cauchy form).
Commutation laws
| Name of the law | Statement of the law |
| First law of commutation (law of conservation of flux linkage) | The magnetic flux coupled to the inductance coils of the circuit, at the moment of commutation, retains the value that it had before commutation, and begins to change precisely from this value: . |
| Second law of commutation (law of conservation of charge) | The electric charge on capacitors connected to any node, at the moment of switching, retains the value that it had before switching, and begins to change precisely from this value: . |
The laws of commutation can be proven by contradiction: if we assume the opposite, then we get infinitely large values of and, which leads to a violation of Kirchhoff’s laws.
In practice, with the exception of special cases (incorrect commutations), it is permissible to use these laws in a different formulation, namely:
first law of commutation -
in the branch with the inductor the current at the moment
.
second law of commutation –
voltage across the capacitor at the moment
commutation retains its pre-commutation value and subsequently begins to change from it: .
It must be emphasized that a more general formulation of the laws of commutation is the provision about the impossibility of abrupt changes at the moment of commutation for circuits with an inductor - flux linkages, and for circuits with capacitors - charges on them. As an illustration of what has been said, the diagrams in Fig. 2, transient processes in which refer to the so-called incorrect switchings
(the name comes from the neglect in such schemes of small parameters, the correct consideration of which can lead to a significant complication of the problem).
Indeed, when translated in the diagram in Fig. 2, and the switch from position 1 to position 2, the interpretation of the second law of commutation as the impossibility of an abrupt change in the voltage on the capacitor leads to failure of the second law of Kirchhoff. Similarly, when opening the key in the circuit in Fig. 2b, the interpretation of the first commutation law as the impossibility of an abrupt change in the current through the inductor leads to the failure of Kirchhoff's first law. For these circuits, based on the conservation of charge and, accordingly, flux linkage, we can write:
Dependent initial conditions are the values of the remaining currents and voltages, as well as derivatives of the desired function at the moment of switching, determined from independent initial conditions using equations compiled according to Kirchhoff's laws for. The required number of initial conditions is equal to the number of integration constants. Since it is rational to write an equation of the form (2) for a variable whose initial value refers to independent initial conditions, the problem of finding the initial conditions usually comes down to finding the values of this variable and its derivatives up to (n-1) order inclusive at.
Conductivity
When novice radio amateurs see an equation for calculating the total resistance of a parallel circuit, they naturally ask, “Where did that come from?” In this article we will try to answer this question.
Due to the fact that electrons, colliding with conductor particles, overcome some resistance to movement, it is customary to say that conductors have electrical resistance
.
Resistance is designated by the letter "R" and is measured in Ohms. However, any conductor can be characterized not only by its resistance, but also by the so-called conductivity
- the ability to conduct electric current. Conductivity is the reciprocal of resistance:
The greater the resistance, the less the conductivity and vice versa. Resistance and conductivity are opposite ways of referring to the same electrical property of materials. If, when comparing the resistances of two components, it turns out that the resistance of component "A" is half that of component "B", then we can alternatively express this relationship by saying that the conductivity of component "A" is twice the conductance of component "B". If the resistance of component "A" is one-third that of component "B", then component "A" can be said to be three times more conductive than component "B", and so on.
Conductivity is designated by the letter “G”, and its unit of measurement was originally “Mo”, that is, “Ohm” written backwards. But, despite the relevance of this unit, it was later replaced by “Siemens” (abbreviated as Sm or S).
Now let's go back to our parallel circuit example. When viewed from a resistance perspective, having multiple paths (branches) for electron flow reduces the overall resistance of the circuit because it is easier for electrons to flow through multiple paths than through one path that has some resistance. If we consider a circuit from the point of view of conductivity, then multiple paths for the flow of electrons, on the contrary, increase the conductivity of the circuit.
The total resistance of a parallel circuit is less than any of its individual resistances because multiple parallel branches create less obstruction to the flow of electrons than each resistor individually:
The total conductivity of a parallel circuit is greater than the conductivity of any of its individual branches, since parallel-connected resistors conduct electric current better than each resistor individually:
It would be more accurate to say that the total conductivity of a parallel circuit is equal to the sum of its individual conductances:
Knowing that conductivity is equal to 1/R, we can transform this formula into the following form:
From this formula it can be seen that the total resistance of the parallel circuit will be equal to:
Well, we have found the answer to the question posed at the beginning of the article! You should be aware that conductivity is very rarely used in practice, and therefore this article is purely educational.
Short review:
- Conductivity is the opposite value of resistance.
- Conductivity is designated by the letter “G” and is measured in Mo or Siemens.
- Mathematically, conductivity is the inverse of resistance: G=1/R
Reactive conductivity is due to the presence of capacitance between phases and between phases and ground, since any pair of wires can be considered as a capacitor.
For overhead power lines, the value of linear reactive conductivity is calculated using the formulas:
7,58 ×10 — 6 b
0 р lg
D avg
.
R
pr eq
Cleavage increases b
0 at 21¸33%.
For CLEP, the value of linear conductivity is often calculated using the form
b
0 =
w
×
C
0 .
Capacitance size C
0 is given in the reference literature for various brands of cable.
The reactive conductivity of a network section is calculated using the formula:
B = b
0 ×
l
.
For overhead power lines the value b
0 is significantly less than that of cable power lines,
small, since D
av. overhead power lines >>
D
av. power transmission lines.
Under the influence of voltage, a capacitive current flows in the conductivities (bias current or charging current):
I
c =
V
×
U
f.
The magnitude of this current determines the loss of reactive power in reactive conductivity or the charging power of the power line:
D Q c
=
Q
charge = 3 ×
U
×
I c
=
B
×
U
2 .
In regional networks, charging currents are comparable to operating currents. At U
nom = 110 kV, the value of
Q
c is about 10% of the transmitted active power,
at U
rated = 220 kV –
Q
s
≈ 30%
R. Therefore, it must be taken into account in calculations. In a network with a rated voltage of up to 35 kV, the value of Qc
can be neglected.
Power line equivalent circuit
So, a power line is characterized by active resistance R
l, jet con-
x line
l, active conductivity
G
l, reactive conductivity
V
l. In calculations, power lines can be represented by symmetrical P- and T-shaped circuits (Fig. 4.6).
| R | X | R/2 X/2 | X/2 |
| R/2 | |||
| B /2 | G /2 | B /2 | |
| G | B | ||
| G/2 |
Figure 4.6 – Equivalent circuits for power lines: a) U-shaped; b) T-shaped
The U-shaped scheme is used more often.
Depending on the voltage class, certain parameters of the complete equivalent circuit can be neglected (see Fig. 4.7):
· Overhead power lines with voltage up to 110 kV (D R
core » 0);
· Overhead power lines with voltage up to 35 kV (D R
cor » 0, D
Q
c » 0);
· CLEP voltage 35 kV (reactance » 0)
· CLEP with voltage 20 kV (reactance » 0, dielectric losses » 0);
· CLEP with voltage up to 10 kV (reactance » 0, dielectric losses » 0, D Q
c » 0).
| X | R | X | R | |
| B /2 | B /2 | |||
| A) | b) | |||
| R | ||||
| R | R | |||
| G/2 | B/2 | B/2 | B/2 | B/2 |
| G/2 | ||||
| V) | G) | d) |
Figure 4.7 – Simplified power transmission line equivalent circuits:
a) overhead power lines at U
rated up to 110 kV;
b) overhead power lines at U
rated up to 35 kV;
c) CLEP at U
nom 35 kV;
d) CLEP at U
rated 20 kV;
e) CLEP at U
nom 6-10 kV;
Lecture No. 5
Transformer equivalent circuit parameters
13. General information.
14. Two-winding transformer.
15. Three-winding transformer.
16. Two-winding transformer with a split low-voltage winding.
17. Autotransformer.
General information
At power plants and substations, three-phase and single-phase, two-winding and three-winding power transformers and autotransformers, and single-phase and three-phase power transformers with a split low-voltage winding are installed.
The transformer abbreviation contains the following information sequentially (from left to right):
type of device ( A
– autotransformer, without designation – transformer);
number of phases ( O
– single-phase,
T
– three-phase);
· presence of a split low voltage winding – P
;
· cooling system ( M
– natural circulation of oil and air,
D
– forced air circulation and natural circulation of oil,
MC
– natural circulation of air and forced circulation of oil,
DC
– forced circulation of air and oil, etc.);
· number of windings (without designation - two-winding, T
– three-winding-precise);
· presence of a voltage regulation device under load (OLTC);
· execution ( Z
– protective,
G
– lightning-resistant,
U
– improved,
L
– with cast insulation);
· specific area of application ( C
– for auxiliary systems of power plants,
F
– for electrification of railways);
· rated power in kVA∙A,
· winding voltage class (network voltage to which the transformer is connected) in kV.
Double winding transformer
In electrical diagrams, a two-winding transformer is represented as follows (Fig. 5.1):
| The windings indicate the circuit diagrams | |
| VN | connection of windings (star, star with well- |
| lem, triangle) and operating mode | |
| trawl: | |
| · star – with an isolated neutral | |
| NN | I pour; |
| · star with zero – there is a connection | |
| neutral to ground. | |
| Figure 5.1 – Conventional image | In accordance with the adopted system |
| two-winding | my notation is abbreviation trans- |
| transformer. | |
| formator TDN-10000/110/10 decoding | |
| is converted: three-phase transformer |
ny, two-winding with forced air circulation and natural oil circulation and a voltage regulation system under load. Rated power – 10000 kV∙A, voltage class of the high voltage winding
– 110 kV, low voltage – 10 kV.
In practical calculations, a two-winding transformer is most often represented by an L-shaped equivalent circuit (Fig. 5.2).
| U 1 | R t | X t | U 2 * |
| In t | G t |
Figure 5.2 – L-shaped equivalent circuit of a two-winding transformer
X
t =
X
in +
X
n *.
The active and reactive resistance of the transformer (longitudinal branch) is the sum of the active and reactive resistance of the high-voltage winding and the low-voltage winding reduced to it:
R
t =
R
in +
R
n *;
The transverse branch of the equivalent circuit is represented by active G
t and reactive
Vt
conductivities. Conductivity is usually connected from the side of the primary winding: for step-up transformers - from the side of the low voltage winding, for step-down transformers - from the side of the high voltage winding.
In such an equivalent circuit there is no transformation, that is, there is no ideal transformer. Therefore, in the calculations the secondary voltage U
2 * turns out to be reduced to the voltage of the primary winding.
Active conductivity is caused by active power losses in the transformer steel due to magnetization reversal and eddy currents, reactive conductivity
– magnetizing power. In calculations of electrical network modes, conductivities are replaced by a load equal to no-load losses.
The parameters of the transformer equivalent circuit are determined from two experiments
– idle and short circuit. In the experiments, the following values are determined, which are indicated in the transformer’s passport data:
active power loss in idle mode D P
x in kW;
active power loss in short circuit mode D P
k in kW;
short circuit voltage U
k, in %;
no-load current I
x, in %.
The values of active and reactive resistance are found from short circuit experience (Fig. 5.3). The experiment is performed as follows: the low-voltage winding is short-circuited, and the same voltage ( U
j) so that the rated current flows in both.
| So | How | voltage |
| I 1nom | short | closures |
| I 2nom | much | less nominal |
| U to | cash | voltage |
| transformer, then the heat- | ||
| ri active power in | ||
| conductivity | practically | |
| skis are zero. So | ||
| Figure 5.3 – Short circuit experience | way, | all losses |
| power in operating mode | ||
| two-winding transformer. | ||
| me short | closures | |
| go to heat the windings. Mathematically this can be written: | ||
| D P =3× I 2 | × R . | (5.1) |
| To | 1nom | T |
If in formula (5.1) the current value is written in terms of the power and rated voltage of the high voltage winding
Short circuit voltage U
k consists of the voltage drop across the active
U
k a and reactive
U
k p resistances. Let's express them as a percentage of the rated voltage.
Voltage drop in the active resistance of the transformer:
| U | to a | 3 ×I | ×R | ||
| U | , % = | ×100 = | 1nom | T | ×100. |
| to a | U in nom | U in nom |
R into the expression
t. We get:
| ×D P × U 2 | |||||||||
| 3 ×I | ×R | 3 ×I | D P | ||||||
| U | , % = | 1nom | T | ×100 | = | 1 room per room | ×100 = | To | ×100. |
| to a | |||||||||
| U in nom | U in nom × S nom 2 | S nom |
Thus, the magnitude of the voltage drop in the active resistance, expressed as a percentage, is proportional to the active power losses in short-circuit mode.
The expression for the voltage drop in reactance in percent is as follows:
| U to p | |||||
| 3 ×I | ×X | T | |||
| U | , % = | ×100 = | 1nom | ×100. | (5.2) |
| k p | U in nom | U in nom |
From it we can find the value of the reactance of the transformer:
| X t = | U cr × U in nom | . |
| × | 3 × I 1 nom |
Multiply and divide the resulting expression by U
in nom:
| X t = | U cr × U in nom | × | U in nom | = | U cr × U in 2 nom | . |
| U in nom | 100 × S nom | |||||
| × 3 | × I 1 nom |
In modern transformers, active resistance is much greater than reactive resistance. Therefore, in practical calculations it can be assumed that U
k r ≈
U
k. Then, the formula for calculating the inductive reactance of a transformer has the form:
| X | = | U to × U to 2 | nom | . |
| T | ||||
| × S nom |
Transformers have voltage regulation devices (on-load tap-changer or tap-changer), which allow changing transformation ratios. Therefore,
rank U
k (hence, the magnitude of the inductive reactance) depends on the branching of the on-load tap-changer or tap-changer devices. In calculations of steady-state conditions, this dependence is neglected. It is taken into account when calculating short-circuit currents when choosing automation and relay protection devices.
The conductivities of the magnetization branch are determined from the no-load test (Fig. 5.4), which is performed at rated voltage. In this mode, the transformer consumes power equal to the no-load losses:
I
2 = 0
Figure 5.4 – Experience of no-load operation of a two-winding transformer.
| G | = | D P x | . |
| T | |||
| U in 2 | |||
| nom |
D S
x = D
P
x +
j
D
Q
x.
Active power losses are proportional to the active conductivity of the transformers
D P
x =
U
in 2 nom ×
G
t.
From here the amount of active conductivity can be determined
Reactive power losses are proportional to the reactive conductivity of the transformer:
D Q
x =
U
in 2 nom ×
B
t.
Therefore, the value of the reactive conductivity of the transformer is equal to:
B
t = D
Q
x.
U
in 2 rooms
The amount of reactive power loss is proportional to the magnetizing current
| D Q x =3× I m × U in nom f, | (5.3) |
where U
nom f – phase rated voltage of the transformer.
The magnitude of the no-load current is the sum of the magnetizing current I
μ and then in steel
I
steel:
I
x=
I
μ+
I
steel.
Since the current value in steel is about 10% of the magnetization current, expression (5.3) can be written:
D Q
x »3×
I
x ×
U
in nom f.
In the passport data, the no-load current value is given as a percentage of the rated current. Therefore we can write:
Taking into account the obtained expression, the formula for calculating reactive conductivity has the form:
B
t =
I
x % × ×
S
nom.
In Fig. 14.14, and the same circuit elements that were considered are connected in parallel (see Fig. 14.7, a). Let us assume that for this circuit the voltage u = U m sinωt
. and parameters of the circuit elements R, L, C. It is required to find the currents in the circuit and power.
Active and reactive conductivity of overhead and cable lines.
Answer: R=ro·l, where ro is linear active resistance (Ohm/km). The active resistance of overhead and cable lines is determined by the material of the current-carrying conductors and their cross-section. To some extent, it depends on the temperature of the conductors and the frequency of the alternating current flowing through them. However, this influence is small and is usually not taken into account when calculating electrical networks. Therefore, resistance values r0 for each brand of wire or cable are usually taken according to tables corresponding to direct current transmission and temperature +20ºС. r0t= r020·(1+α(t-20)), where α is the temperature coefficient; r020 – resistance at 20 ºС. When making estimation calculations for conductors made of non-ferrous metals, the active resistance can be determined by the formula: r0=ρ/F, where ρ is the resistivity (Ohm mm2/km), F is the cross-section of the conductor (mm2).
G=g0·l, where g0 is specific active conductivity (S/km). The conductivity due to corona losses is highly variable and depends on air humidity and other meteorological conditions. The average value of active conductivity for a year is obtained through the average losses to the corona ΔPк: ; , where ΔPkud - specific average annual losses per corona (kW/km).
Corona power losses are taken into account for overhead lines with Unom 330 kV and above. In 110-220 kV overhead lines, these losses can be ignored, because The PUE has established minimum wire cross-sections to reduce ΔPк to acceptable levels. For 110 kV overhead line - AS 70/11, 220 kV overhead line - AS 240/32.
The most radical means of reducing power losses to the crown is to increase the diameter of the wire. X=x0·l, where x0 is the linear inductive reactance (Ohm/km).
Inductive reactance is caused by the magnetic field that arises around and inside the wires and cores of cables, which induces an electromotive force of self-induction in each conductor. Inductive reactance depends on the relative position of the conductors, their diameter and magnetic permeability and frequency of alternating current. For overhead lines with aluminum and steel-aluminum wires, the resistance per 1 km is calculated: x0=0.144·lg(2·Dav/d)+0.0156, where Dav is the geometric mean distance between the phase wires, mm, d is the wire diameter, mm.
Dav depends on the type of support arrangement and Unom Dav = , where DAB, DBC, DCA is the distance between the wires of the corresponding phases.
For overhead lines, the values of x0 are given in the reference table depending on Dav or voltage and type of wire. The inductive reactance of cable lines is influenced by the design features of the cables. When making calculations, use the factory data on x0 given in the reference book. The reactive conductivity of the line is caused by the capacitances between the wires of different phases and the wire-to-ground capacitance. It is determined by the formula: , B=b0·l, where b0 is the specific reactive (capacitive) conductivity, Ohm/km. For overhead lines, specific capacitive conductivity can be found as or determined from reference tables, depending on the type of wire and the geometric mean distance between the wires or nom. voltage. The capacitive conductivity of cable lines depends on the cable design and is indicated by the manufacturer, but for approximate calculations it can be estimated using the formula. It is obvious that the value of b0 for cable lines is much greater than for overhead lines due to the lower values of Dav.
Answer: R=ro·l, where ro is linear active resistance (Ohm/km). The active resistance of overhead and cable lines is determined by the material of the current-carrying conductors and their cross-section. To some extent, it depends on the temperature of the conductors and the frequency of the alternating current flowing through them. However, this influence is small and is usually not taken into account when calculating electrical networks. Therefore, resistance values r0 for each brand of wire or cable are usually taken according to tables corresponding to direct current transmission and temperature +20ºС. r0t= r020·(1+α(t-20)), where α is the temperature coefficient; r020 – resistance at 20 ºС. When making estimation calculations for conductors made of non-ferrous metals, the active resistance can be determined by the formula: r0=ρ/F, where ρ is the resistivity (Ohm mm2/km), F is the cross-section of the conductor (mm2).
G=g0·l, where g0 is specific active conductivity (S/km). The conductivity due to corona losses is highly variable and depends on air humidity and other meteorological conditions. The average value of active conductivity for a year is obtained through the average losses to the corona ΔPк: ; , where ΔPkud - specific average annual losses per corona (kW/km).
Corona power losses are taken into account for overhead lines with Unom 330 kV and above. In 110-220 kV overhead lines, these losses can be ignored, because The PUE has established minimum wire cross-sections to reduce ΔPк to acceptable levels. For 110 kV overhead line - AS 70/11, 220 kV overhead line - AS 240/32.
The most radical means of reducing power losses to the crown is to increase the diameter of the wire. X=x0·l, where x0 is the linear inductive reactance (Ohm/km).
Inductive reactance is caused by the magnetic field that arises around and inside the wires and cores of cables, which induces an electromotive force of self-induction in each conductor. Inductive reactance depends on the relative position of the conductors, their diameter and magnetic permeability and frequency of alternating current. For overhead lines with aluminum and steel-aluminum wires, the resistance per 1 km is calculated: x0=0.144·lg(2·Dav/d)+0.0156, where Dav is the geometric mean distance between the phase wires, mm, d is the wire diameter, mm.
Dav depends on the type of support arrangement and Unom Dav = , where DAB, DBC, DCA is the distance between the wires of the corresponding phases.
For overhead lines, the values of x0 are given in the reference table depending on Dav or voltage and type of wire. The inductive reactance of cable lines is influenced by the design features of the cables. When making calculations, use the factory data on x0 given in the reference book. The reactive conductivity of the line is caused by the capacitances between the wires of different phases and the wire-to-ground capacitance. It is determined by the formula: , B=b0·l, where b0 is the specific reactive (capacitive) conductivity, Ohm/km. For overhead lines, specific capacitive conductivity can be found as or determined from reference tables, depending on the type of wire and the geometric mean distance between the wires or nom. voltage. The capacitive conductivity of cable lines depends on the cable design and is indicated by the manufacturer, but for approximate calculations it can be estimated using the formula. It is obvious that the value of b0 for cable lines is much greater than for overhead lines due to the lower values of Dav.
Vector diagram for a circuit with parallel connections of branches. Vector diagram method
For instantaneous quantities, in accordance with Kirchhoff’s first law, the current equation
Representing the current in each branch as the sum of the active and reactive components, we obtain
For effective currents you need to write a vector equation
The numerical values of the current vectors are determined by the product of the voltage and conductivity of the corresponding branch.
In Fig. 14.14, b a vector diagram corresponding to this equation is constructed. As usual when calculating circuits with parallel
connections of branches, vector
U is taken as the initial vector,
and then the current vectors in each branch are plotted, and their directions relative to the voltage vector are chosen in accordance with the nature of the conductivity of the branches. The starting point when constructing a current diagram is the point coinciding with the beginning of the voltage vector. From this point the vector l 1a of the active current
of branch
I
(in phase with the voltage), and from its end the vector
I 1p
of the reactive current of the same branch is drawn (leads the voltage by 90°).
These two vectors are components of the vector I 1 of the first branch current
.
Next, the current vectors of other branches are plotted in the same order. It should be noted that the conductivity of branch 3-3 is active
, therefore the reactive component of the current in this branch is zero.
In branches 4-4 and 5-5, the conductivities are reactive
, therefore there are no active components in the composition of these currents.
Calculation of basic parameters
Link options
Power lines, transformers and switches can act as connections, that is, circuit elements that connect two circuit nodes. Let's consider how their parameters are determined.
Power lines
As a rule, when calculating steady-state conditions on a PC, the power transmission line is represented by a U-shaped equivalent circuit (Figure 1).
A power line is characterized by longitudinal resistance and transverse conductivity
Conductance
The active conductivity of overhead lines is almost entirely determined by corona losses, and therefore it strongly depends not only on the design of the line, but also on the operating voltage and weather conditions. In overhead lines (OHL) with voltages up to 220 kV, power losses to the corona are usually neglected, and the value is taken equal to zero. For overhead lines with a voltage of 220 kV and above, the values of corona losses Pk for a given type of weather are included in the loads, or the active conductivities can be calculated in the equivalent circuit:
where: Pok - specific corona losses, taken from the reference book for a given type of line and for a given type of weather, kW/km;
l—line length, km;
Unom - rated voltage, kV.
For cable lines, active conductivity determines the loss in cable insulation. They are characterized by the dielectric loss tangent, determined according to the manufacturer’s data:
In cable lines with voltages up to 110 kV, these losses are usually neglected and taken equal to zero.
The values of , , are determined by the length of the line between adjacent nodes of the design diagram and the values of the specific parameters: The values of r0, x0, b0 are given in the reference literature, and they can also be calculated using the following formulas, taking into account the design features of power lines.
Active resistance
For aluminum and steel-aluminum wires, the resistivity at a temperature of +20 0C can be approximately determined from the expression:
, Ohm/km,
where: F is the calculated wire cross-section, mm2.
In the case when the phase consists of n wires (components), the value obtained from the above formula must be divided by n.
When making calculations related to determining electricity losses in overhead lines, it is necessary to take into account the dependence of the active resistance of the line on the temperature of the wire: where:
– average temperature for the base period, 0С;
– specific active resistance at a temperature of +20 0C.
Inductive reactance
The specific inductive reactance of an overhead line wire depends not only on the size of the wire itself, but also on the distance between the phases, and for ultra-high voltage lines, the phase of which may consist of several wires, also on the number of components in the phase and on the distance between them.
where: r – radius of a single wire, m;
— geometric mean distance between phases, m.
If the overhead line phase consists of n wires, then in the above expression instead of the value r the value should be substituted:
where: r – radius of a single wire, m,
a – geometric mean distance between wires of one phase, m.
For cable lines, the inductive reactance is less than for air lines, since the geometric mean distance between the phases is much smaller. Therefore, when calculating modes for cable networks of 10 kV and below, only active resistance can be taken into account.
Capacitive conductivity
Specific conductivity is related to the specific capacitance of overhead lines by the relation: where:
– angular frequency.
In turn, the capacity of an overhead line depends on the diameter of the wires, their relative position and the distance between them.
If we do not take into account the influence of neighboring overhead line circuits and lightning protection cables (which introduces an error not exceeding 5%), then the specific capacitive conductivity of an overhead line with one wire in phase is determined as
With n components in phase in the above formula, instead of r, the value rе should be substituted, determined by the formula:
For overhead lines with voltages below 110 kV, capacitive conductivity can be ignored.
The capacitive conductance of cable lines depends on the cable design and is indicated by the manufacturer, but for approximate calculations it can be estimated using the same formula. Capacitive conductivity in cable lines is greater than in air lines, since the distances between the wires are much smaller.
Calculation formulas for a circuit with parallel connections of branches. Vector diagram method
From a vector diagram
it can be seen that all the active components of the current vectors are directed in the same way - parallel to the voltage vector, so their vector addition can be replaced with arithmetic ones to find the active component of the total current:
I a = I 1a + I 2a + I 3a
.
Reactive components
current vectors are perpendicular to the voltage vector, with inductive currents directed in one direction, and capacitive currents in the other.
Therefore, the reactive component of the total current in the circuit is determined by their algebraic sum, in which inductive currents are considered positive and capacitive currents are considered negative: I p = - I 1p + I 2p - I 4p + I 5p
.
The active, reactive and total current vectors of the entire circuit form a right triangle, from which it follows
Attention should be paid to possible errors when determining the total conductivity of a circuit from the known conductivities of individual branches:
it is impossible
to add arithmetically the conductivities of the branches if the currents in them are out of phase.
Full conductivity
circuits are generally defined as the hypotenuse of a right triangle, the legs of which are the active and reactive conductivities of the entire circuit expressed on a certain scale:
From the current triangle you can also go to the power triangle and to determine the power you can obtain the already known formulas
Active power
circuits can be represented as the arithmetic sum of the active powers of the branches.
Reactive power
chain is equal to the algebraic sum of the powers of the branches. In this case, the inductive power is taken to be positive, and the capacitive power to be negative: