To maintain an electric current in a conductor for a long time, it is necessary that the charges delivered by the current are constantly removed from the end of the conductor, which has a lower potential (consider that current carriers are assumed to be positive charges), while charges are constantly supplied to the end with a higher potential. That is, it is necessary to ensure the circulation of charges. In this cycle, charges must move along a closed path. The movement of current carriers is realized using forces of non-electrostatic origin. Such forces are called third parties. It turns out that to maintain the current, external forces are needed that act along the entire length of the circuit or in individual sections of the circuit.
Definition and formula of EMF
Definition
A scalar physical quantity that is equal to the work of external forces to move a unit positive charge is called electromotive force (EMF)
, acting in a circuit or section of a circuit.
EMF is denoted by $\varepsilon$ . Mathematically, we write the definition of EMF as: $$\varepsilon=\frac{A}{q}(1)$$
where A is the work of external forces, q is the charge on which the work is performed.
The electromotive force of the source is numerically equal to the potential difference at the ends of the element if it is open, which makes it possible to measure the EMF by voltage.
The EMF that acts in a closed circuit can be defined as the circulation of the tension vector of external forces:
$$\varepsilon=\oint_{L} \bar{E}^{*} d \bar{l}(2)$$
where $\bar{E}^{*}$ is the field strength of external forces. If the field strength of external forces is not zero only in part of the circuit, for example, on segment 1-2, then integration in expression (2) can be carried out only over this section. Accordingly, the EMF acting on circuit section 1-2 is defined as:
$$\varepsilon=\int_{1}^{2} \bar{E}^{*} d \bar{l}(3)$$
Formula (2) gives the most general definition of EMF, which can be used for any cases.
INFOFIZ
A short-term current in a conductor can be obtained by connecting two charged conducting bodies that have different potentials with this conductor. The current in the conductor will disappear when the potential of the bodies becomes the same. For an electric current to exist
and maintain in it .
Direct electric current can only be created in a closed circuit
, in which free charge carriers circulate along closed trajectories.
When an electric charge moves in an electrostatic field along a closed path, the work done by electric forces is zero. Therefore, for the existence of direct current, it is necessary to have a device in the electrical circuit that is capable of creating and maintaining potential differences in sections of the circuit due to the work of forces of non-electrostatic origin
. The field inside the conductors making up a closed circuit must be supported by a source of electrical energy.
Devices capable of creating and maintaining potential differences in sections of a circuit due to the work of forces of non-electrostatic origin.
are called direct current sources
.
Forces of non-electrostatic origin acting on free charge carriers from current sources are called
extraneous forces
.
The nature of external forces may vary. In galvanic cells or batteries they arise as a result of electrochemical processes; in direct current generators, external forces arise when conductors move in a magnetic field. Under the influence of external forces, electric charges move inside the current source against
electrostatic field forces, due to which a constant electric current can be maintained in a closed circuit.
The circuit also includes consumers
electrical energy
in which the current performs useful work.
In addition, the circuit includes
connecting wires
and
a switch (switch)
to close and open the circuit. A simple electrical circuit consists of a current source, a consumer, supply wires and a switch.
A DC circuit can be divided into specific sections. Those areas that are not affected by external forces (that is, areas that do not contain current sources) are called homogeneous
.
Areas that include current sources are called inhomogeneous
.
The figure shows a closed DC circuit. Chain section ( cd
) is homogeneous.
Part of a circuit in which charges move in the direction of electrical forces ( a- d- c- b)
is called
external
, and the part of the circuit in which the charges move in the direction of the action of external forces (
a- b
) is called
internal
.
Those points at which the external circuit borders on the internal circuit are called poles.
One of the poles has the highest potential and the other has the lowest potential compared to other points in the circuit.
The pole with the highest potential is called positive
and is denoted by a “+” sign, and the pole with the lowest potential is called
negative
and is denoted by a “-” sign.
When a single positive charge moves along a certain section of the circuit, work is performed by both electrostatic (Coulomb) and external forces.
a direct current source in the electrical circuit
a device capable of creating and maintaining potential differences across sections of a circuit. The appearance of a potential difference at the poles of any source is the result of the separation of positive and negative charges in it. This separation occurs due to the work done by outside forces. When electric charges move along a direct current circuit, external forces acting inside the current sources perform work.
A physical quantity equal to the ratio of the work Ast of external forces when moving a charge q from the negative pole of a current source to the positive one to the value of this charge is called
the electromotive force of the source (EMF):
EMF is determined by the work done by external forces when moving a single positive charge.
Electromotive force, like potential difference, is measured in volts
[IN].
To measure the emf of a source, you need to connect to it with an open circuit .
The current source is a conductor and always has some resistance, so the current generates heat in it. This resistance is called internal source resistance
and denoted by
r
.
When a single positive charge moves along a closed direct current circuit, the work done by external forces is equal to the sum of the emf acting in this circuit, and the work done by the electrostatic field is zero.
The work of external forces to move a unit charge is equal, by definition, to the electromotive force ε12 acting in a given area. Therefore, the total work done to move a unit charge is equal to
U value
12, equal to the work of moving a unit charge, is usually called
the voltage
on the circuit section 1–2.
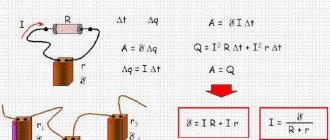
If the circuit consists of an external part with a resistance R and an internal part with a resistance r, then, according to the law of conservation of energy, the emf of the source will be equal to the sum of the voltages on the external and internal sections of the circuit, because when moving along a closed circuit, the charge returns to its original position, where IR is the voltage on the external section of the circuit, and Ir is the voltage on the internal section of the circuit.
Thus, for a section of the circuit containing EMF:
This formula expresses Ohm's law for a complete circuit
:
the current strength in a complete circuit is directly proportional to the electromotive force of the source and inversely proportional to the sum of the resistances of the external and internal sections of the circuit.
The figure shows a closed DC circuit.
Continuation of the lecture
Ohm's law for an arbitrary section of a circuit
The section of the chain on which external forces act is called heterogeneous. It satisfies the following equality:
$$U_{12}=\varphi_{1}-\varphi_{2}+\varepsilon_{12}(4)$$
where U12=IR21 – voltage drop (or voltage) in circuit section 1-2 (I-current); $\varphi_{1}-\varphi_{2}$ – potential difference between the ends of the section; $\varepsilon_12$ is the electromotive force contained in the circuit section. $\varepsilon_12$ is equal to the algebraic sum of the emf of all sources that are located in a given area.
It should be taken into account that EMF can be positive and negative. The EMF is called positive if it increases the potential in the direction of the current (the current flows from the minus to the plus of the source).
Current source. Outside forces. EMF of current source
Let us dwell on individual patterns of conduction current. Let at the ends of a conductor of length l
there is a potential difference
Δφ=φ1–φ2=U, which creates an electric field inside it with intensity E , directed in the direction of the potential drop (Fig. 92).
| j |
| l |
Rice. 92
.
In this case, a current will arise in the conductor from a higher potential φ1 to a lower potential φ2.
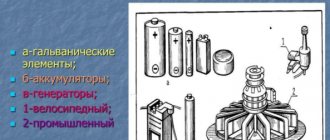
The movement of charges from φ1 to φ2 leads to a decrease in the larger (φ1) and an increase in the smaller (φ2) potential, i.e. to equalize potentials. As soon as the potentials are equalized, the electric field in the conductor will disappear and the current will stop. Thus, to maintain an electric current, it is necessary to have special devices that would maintain a potential difference at its ends. Such a device is called a current source . Current sources are electric generators, galvanic and thermoelements, and batteries. The direction of current in the device is opposite to the direction of current in the conductor. The current source also plays another role - it closes the circuit through which the continuous movement of charges occurs. Current flows through the outer part of the circuit - the conductor - and through the inner part - the current source. The current source has two poles: positive with a higher potential and negative with a lower potential. When the circuit is open, an excess of electrons is formed at the negative pole (terminal) of the current source, and a deficiency is formed at the positive pole. The separation of charges in a current source is carried out with the help of external forces, the so-called external forces , directed against the Coulomb forces acting on unlike charges in the conductors of the current source itself. The nature of these external forces can be very different (chemical, mechanical, electromagnetic).
Fig.93
If a circuit consisting of a conductor and a current source is closed, then a current passes through it and at the same time the work of external forces Ac is performed. (Fig. 93). This work consists of the work done against the forces of the electric field inside the current source (Aist.) and the work done against the mechanical resistance forces of the source environment (A'), i.e. Ast. = Stork + A'.
The value equal to the ratio of the work done by external forces when moving a point positive charge Q along the entire circuit (including the current source) to the amount of charge Q is called the emf of the current source ε
ε
= .
The work done against the electric field forces (by definition) is equal to
Stork. = Q ( φ1 – φ2).
If the poles of the source are open, then A' = 0, and then from the formula ε
follows ε
= φ1 – φ2, i.e. The EMF of the current source when the external circuit is open is equal to the potential difference that is created at its poles.
Let us dwell on individual patterns of conduction current. Let at the ends of a conductor of length l
there is a potential difference
Δφ=φ1–φ2=U, which creates an electric field inside it with intensity E , directed in the direction of the potential drop (Fig. 92).
| j |
| l |
Rice. 92
.
In this case, a current will arise in the conductor from a higher potential φ1 to a lower potential φ2.
The movement of charges from φ1 to φ2 leads to a decrease in the larger (φ1) and an increase in the smaller (φ2) potential, i.e. to equalize potentials. As soon as the potentials are equalized, the electric field in the conductor will disappear and the current will stop. Thus, to maintain an electric current, it is necessary to have special devices that would maintain a potential difference at its ends. Such a device is called a current source . Current sources are electric generators, galvanic and thermoelements, and batteries. The direction of current in the device is opposite to the direction of current in the conductor. The current source also plays another role - it closes the circuit through which the continuous movement of charges occurs. Current flows through the outer part of the circuit - the conductor - and through the inner part - the current source. The current source has two poles: positive with a higher potential and negative with a lower potential. When the circuit is open, an excess of electrons is formed at the negative pole (terminal) of the current source, and a deficiency is formed at the positive pole. The separation of charges in a current source is carried out with the help of external forces, the so-called external forces , directed against the Coulomb forces acting on unlike charges in the conductors of the current source itself. The nature of these external forces can be very different (chemical, mechanical, electromagnetic).
Fig.93
If a circuit consisting of a conductor and a current source is closed, then a current passes through it and at the same time the work of external forces Ac is performed. (Fig. 93). This work consists of the work done against the forces of the electric field inside the current source (Aist.) and the work done against the mechanical resistance forces of the source environment (A'), i.e. Ast. = Stork + A'.
The value equal to the ratio of the work done by external forces when moving a point positive charge Q along the entire circuit (including the current source) to the amount of charge Q is called the emf of the current source ε
ε
= .
The work done against the electric field forces (by definition) is equal to
Stork. = Q ( φ1 – φ2).
If the poles of the source are open, then A' = 0, and then from the formula ε
follows ε
= φ1 – φ2, i.e. The EMF of the current source when the external circuit is open is equal to the potential difference that is created at its poles.
Electromotive force as a measure of external forces
So, the action of the current source is to, with the help of external forces, perform work on the transfer of electric charges between the poles against the action of the electric field. To characterize this work, there is a special measure called electromotive force (EMF, denoted by the letter $\mathscr{E}$). Its physical meaning is that it is the work of external forces to transfer a unit of charge. That is, the EMF is equal to the ratio of the work done by external forces to transfer charge against the action of the electric field to the magnitude of this charge:
$$\mathscr{E} = {A_{st}\over q}$$
From this formula you can obtain the unit of measurement of EMF. It is the same as voltage - Volt (remember, 1 V = 1 J / 1 C).
The EMF of a regular AA battery is 1.5V. That is, in it, external forces of a chemical nature perform 1.5 J of work to transfer 1 C of charge.
Rice. 3. AA batteries.
Electromotive force. Ohm's law for a complete circuit
As you know, for an electric current to exist, an electric field must be present. Moreover, this field must be constantly maintained by some current source. Today we will talk about the main characteristic of a current source, which is called electromotive force (or, in short, EMF). First, let's consider a simple experiment: take two oppositely charged balls and connect them with a conductor. In this case, an electric current will arise in the conductor, but it will be very short-lived. The fact is that very soon a redistribution of charge will occur, and the potentials of the balls will be equalized. This means that the electric field will cease to exist.
From this we can conclude that in order to maintain a constant current, the presence of certain forces of non-electric origin is necessary so that these forces can move charges against the field. Such forces are called external forces. That is, third-party forces are any forces that act on electric charges, but are not forces of electrical origin
. For example, these could be forces acting on charges from a magnetic field - this is used in generators.
In batteries or accumulators, the work of separating electrical charges is done by chemical reactions.
Another argument that we can give is that the work done by Coulomb forces when moving a charge along a closed loop is zero
. This means that some other forces must provide non-zero work to maintain the potential difference.
A device for maintaining electric current is called a current source.
In any current source, external forces act on the charges, doing work against the Coulomb forces.
Therefore, the characteristic of the source must be a value independent of the magnitude of the charge. This quantity is called electromotive force. The electromotive force is equal to the ratio of the work of external forces when moving a charge along a closed circuit to the magnitude of this charge:
From the formula it is clear that the electromotive force, like voltage, is measured in volts:
Now that we are familiar with EMF, we can move on to studying Ohm's law for a complete circuit. A complete circuit is a closed circuit that includes a current source.
For convenience, we will consider the simplest electrical circuit, consisting only of a current source, a resistor and connecting wires:
As we have already said, a current source is characterized by an emf. However, any current source has a certain resistance, which is called internal resistance
. Ohm's law for a complete circuit represents the relationship between emf, internal and external resistance, and current in the circuit. In order to establish this connection, we use the law of conservation of energy. Let us write that the work of external forces is equal to the product of the source emf and the magnitude of the charge:
As you know, each section of the circuit emits a certain amount of heat. According to the Joule-Lenz law, this amount of heat is calculated by the formula:
Based on the law of conservation of energy, we can equate this amount of heat to the work of external forces:
Ohm's law for a complete circuit sounds like this: the current strength in a closed circuit is equal to the ratio of the source emf to the total resistance of the circuit:
Ohm's law can be derived for a complete circuit using slightly different reasoning. As we know, with a series connection, the total voltage of the circuit is equal to the sum of the voltage drops in all sections of the circuit:
We see that the product of current and resistance of a resistor is nothing more than the voltage across this resistor. And the product of current and internal resistance is the voltage drop across the source itself:
It must be said that the internal resistance of the source in many cases is negligible compared to the resistance of the external part of the circuit. In this case, we can assume that the voltage at the source terminals is approximately equal to the EMF (that is, the voltage drop across the source is considered approximately zero):
However, it is the internal resistance that determines the current strength in the circuit during a short circuit. Let us recall that during a short circuit, the external resistance becomes almost zero, so the current in the circuit increases sharply:
Let us now consider a circuit containing several current sources connected in series.
In this case, the EMF of the entire circuit is equal to the algebraic sum of the EMF of individual sources.
In such cases, it is necessary to select the so-called “current bypass direction”. This direction is chosen conditionally (in our case, counterclockwise). Then, because they tend to induce current in the bypass direction.
A, because they tend to cause a current in the direction opposite to the direction of bypass. Negative EMF means that external forces inside the source do negative work. Thus, the EMF of our circuit will be equal to:
In accordance with the rules of series connection, the total resistance of the circuit is equal to the sum of the external resistance and the internal resistances of all current sources:
An example of solving a problem.
Task.
A resistor with a resistance of 15 Ohms is connected to a current source with an internal resistance of 1 Ohm. After this, an ammeter was connected to the circuit, which showed that the current strength was 5 A. Find the work done by external forces inside the source in 2 minutes.