Period and frequency
These terms are used to express repeated movement. Period is the time spent on one repetition. One full pass is a cycle. Frequency – the number of cycles over a specific time period (f).
Sine waves of different frequencies. The lower ones have higher frequencies, and the horizontal axis displays time.
The concepts are expressed in the formula: F = 1/T.
Let's say the heart rate of a newborn is 120 times per minute, and the period is half a second. If you sharpen your intuition to expect the conjugation of large frequencies with short periods (and vice versa), you will avoid mistakes.
Movement examples
Oscillatory motion is one of the most common in nature. For example, you can imagine the strings of a musical instrument, a swing, or a person's vocal cords.
In physics, oscillations are processes that repeat at regular intervals. Such movements are considered through several models:
- a body suspended on a spring (moving up and down);
- weight on a string;
- electrical circuit and others.
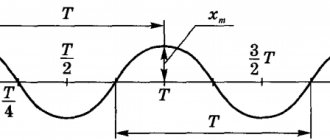
Amplitude and phase of oscillations
The amplitude of oscillations is the modulus of the greatest displacement of the body from the equilibrium position. Designation – \( A\, (X_{max}) \), units of measurement – m.
The oscillation phase is a quantity that determines the state of the oscillatory system at any time. Designation – \( \varphi \), units of measurement – rad (radian).
The oscillation phase is a quantity under the sine or cosine sign. It shows how much of the period has passed since the beginning of the oscillations. The phase of harmonic oscillations changes during the oscillation process. \( \varphi_0 \) – initial phase of oscillations. The initial phase of oscillations is a value that determines the position of the body at the initial moment of time.
Important! The path traveled by a body in one complete oscillation is equal to four amplitudes.
Metrological aspects
Oscillation frequency has found its application even in metrology. Different devices have many functions:
- The pulse frequency is measured. They are represented by electronic counting and capacitor types.
- The frequency of spectral components is determined. There are heterodyne and resonant types.
- Spectrum analysis is carried out.
- Reproduce the required frequency with a given accuracy. In this case, various measures can be used: standards, synthesizers, signal generators and other techniques in this direction.
- The indicators of the obtained oscillations are compared; for this purpose, a comparator or oscilloscope is used.
Resonance
Resonance is the phenomenon of a sharp increase in the amplitude of oscillations, which occurs when the frequency of the driving force and the natural frequency of oscillations of the body coincide.
Resonance condition:
\( v_0 \) – natural frequency of oscillations of the pendulum.
The figure shows resonance curves for media with different friction. The less friction, the higher and sharper the resonance curve.
The phenomenon of resonance is taken into account under periodically changing loads in machines and various structures. Resonance is also used in acoustics, radio engineering, etc.
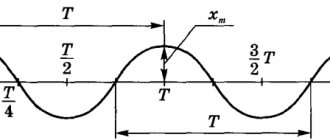
Pendulum
To consider the basic concepts of oscillatory processes, it is convenient to take a pendulum as an example - a small mass suspended on a thin light thread. If you swing it, it will begin to make uniform movements.
Rice. 2. Oscillations of the pendulum.
Each movement of the pendulum, starting from the extreme point and ending at the same point, is called an oscillation.
Example of work: sound
Everything written above can be quite difficult to understand, since we used the dry language of physics. To understand the information provided, you can give an example. Everything will be described in detail, based on an analysis of cases from modern life. To do this, consider the most famous example of vibrations – sound. Its properties, as well as the features of the implementation of mechanical elastic vibrations in the medium, are directly dependent on the frequency.
The human hearing organs can detect vibrations that range from 20 Hz to 20 kHz. Moreover, with age, the upper limit will gradually decrease. If the frequency of sound vibrations drops below 20 Hz (which corresponds to the mi subcontractive), then infrasound will be created. This type, which in most cases is not audible to us, people can still feel tactilely. When the limit of 20 kilohertz is exceeded, oscillations are generated, which are called ultrasound. If the frequency exceeds 1 GHz, then in this case we will be dealing with hypersound. If we consider a musical instrument such as a piano, it can create vibrations in the range from 27.5 Hz to 4186 Hz. It should be taken into account that musical sound does not consist only of the fundamental frequency - overtones and harmonics are also mixed into it. All this together determines the timbre.
Hertz is a unit of measurement of the frequency of a periodic process in the SI system
Definition
The frequency of periodic processes ($\nu$) is a physical quantity that is equal to the number of cycles that occur per unit time. This definition says that:
\[\nu =\frac{1}{T}\left(1\right),\]
where $T$ is the process period.
From expression (1) it is obvious that the unit of measurement of frequency is the reciprocal second:
\[\left[\nu \right]=с^{-1}.\]
In the International System of Units (SI), this unit of measurement has a special name; it has been called hertz (Hz) since 1960 (the beginning of the system). Hertz is a unit of measurement of the frequency of a periodic process, at which one process cycle occurs in one second.
The unit for measuring the frequency of a periodic process is named after the German scientist G. Hertz, who worked extensively and successfully in electrodynamics.
Hertz, as a unit of measurement of frequency, can be used with standard SI prefixes to denote decimal multiples and submultiples. For example, GHz (hectohertz): $1g\Hz=100\Hz$; µHz (microhertz): $1 µHz={10}^{-6}Hz.$ The beat of a healthy human heart in a calm state occurs at a frequency of 1 Hz.
Sometimes the frequency of periodic oscillations is denoted by the letter $f$.
Often in calculations, the cyclic frequency (angular frequency, radial frequency, circular frequency) ($\omega $) is used, which is equal to:
\[\omega =2\pi {\mathbf \nu }\left(2\right).\]
Angular frequency is measured in radians divided per second:
\[\left[\omega \right]=\frac{rad}{s}.\]
In the SI and GHS systems, the units of measurement of circular frequency are the same.
Harmonic vibrations
Harmonic oscillations are the simplest periodic oscillations in which the coordinate of a body changes according to the law of sine or cosine:
where \( x \) – body coordinate – displacement of the body from the equilibrium position at a given time; \( A \) – vibration amplitude; \( \omega t+\varphi_0 \) – oscillation phase; \( \omega \) – cyclic frequency; \( \varphi_0 \) – initial phase.
If at the initial moment of time the body passes the equilibrium position, then the oscillations are sinusoidal.
If at the initial moment of time the displacement of the body coincides with the maximum deviation from the equilibrium position, then the oscillations are cosine.
Speed of harmonic oscillations The speed of harmonic oscillations is the first derivative of the coordinate with respect to time:
where \( v \) is the instantaneous value of the speed, i.e. the speed at a given time.
Speed amplitude is the maximum value of the oscillation speed, this is the value preceding the sine or cosine sign:
Acceleration of harmonic oscillations Acceleration of harmonic oscillations is the first derivative of speed with respect to time:
where \( a \) is the instantaneous value of acceleration, i.e. acceleration at a given time.
Acceleration amplitude is the maximum acceleration value, this is the value preceding the sine or cosine sign:
If a body performs harmonic oscillations, then the force acting on the body also changes according to the harmonic law:
where \( F \) is the instantaneous value of the force acting on the body, i.e. the force at a given moment in time.
Force amplitude – the maximum value of the force, the value preceding the sine or cosine sign:
A body performing harmonic vibrations has kinetic or potential energy:
where \( W_k \) is the instantaneous value of kinetic energy, i.e. kinetic energy at a given moment in time.
The amplitude of kinetic energy is the maximum value of kinetic energy, the value preceding the sine or cosine sign:
With harmonic oscillations, every quarter of the period there is a transition of potential energy into kinetic energy and vice versa. In the equilibrium position:
- potential energy is zero;
- kinetic energy is maximum.
At maximum deviation from the equilibrium position:
- kinetic energy is zero;
- potential energy is maximum.
Total mechanical energy of harmonic vibrations With harmonic vibrations, the total mechanical energy is equal to the sum of the kinetic and potential energies at a given time:
Important! It should be remembered that the period of oscillations of kinetic and potential energies is 2 times less than the period of oscillations of coordinates, speed, acceleration and force. And the frequency of oscillations of kinetic and potential energies is 2 times greater than the frequency of oscillations of coordinates, speed, acceleration and force.
Graphs of the dependence of kinetic, potential and total energies always lie above the time axis.
If there is no resistance force, then the total energy is conserved. The graph of total energy versus time is a straight line parallel to the time axis (in the absence of friction forces).
Sample. Volume. Scope
What is sampling? In simple terms, this is the information we selected for research. For example, we can form the following sample - the amount of money spent on each of six days. Let's draw a table in which we will enter expenses for six days
The sample consists of n-elements. The variable n can be replaced by any number. We have six elements, so n is 6
n=6
Elements of the sample are designated using subscripted variables. The last element is the sixth element of the selection, so n will be replaced by the number 6.
Let's denote the elements of our sample by variables
The number of sample elements is called sample size . In our case, the volume is six.
range is the difference between the largest and smallest element in the sample.
In our case, the largest element in the sample is element 250, and the smallest element is element 150. The difference between them is 100
Discrete event frequency, rotation speed
Definition of frequency of discrete oscillations
($n$) - called a physical quantity that is equal to the number of actions (events) per unit of time.
If the time that one event takes is denoted as $\tau $, then the frequency of discrete events is equal to:
\[n=\frac{1}{\tau }\left(7\right).\]
The unit of measurement for discrete event frequency is the reciprocal second:
\[\left[n\right]=\frac{1}{s}.\]
A second to the minus first power is equal to the frequency of discrete events if one event occurs in a time equal to one second.
Rotation frequency ($n$) is a value equal to the number of full revolutions a body makes per unit time. If $\tau$ is the time spent on one full revolution, then:
\[n=\frac{1}{\tau }\left(8\right).\]