Oscillation period.
The period of oscillation is the shortest period of time through which a system oscillating returns again to the same state in which it was at the initial moment of time, chosen arbitrarily.
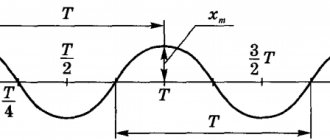
In other words, the period of oscillation (T) is the time during which one complete oscillation occurs. For example, in the figure below, this is the time during which the pendulum bob moves from the extreme right point through the equilibrium point O to the extreme left point and back through point O again to the extreme right.
Over a full period of oscillation, the body thus travels a path equal to four amplitudes. The period of oscillation is measured in units of time - seconds, minutes, etc. The period of oscillation can be determined from a well-known graph of oscillations (see figure below).
The concept of “oscillation period,” strictly speaking, is valid only when the values of the oscillating quantity are exactly repeated after a certain period of time, that is, for harmonic oscillations. However, this concept also applies to cases of approximately repeating quantities, for example, for damped oscillations .
Math pendulum
Definition A mathematical pendulum is a special case of a physical pendulum, the mass of which is located at one point.
Typically, a mathematical pendulum is considered to be a small ball (material point) having a large mass, suspended on a long inextensible thread (suspension). This is an idealized system that oscillates under the influence of gravity. Only for angles of the order of 50-100, a mathematical pendulum is a harmonic oscillator, that is, it performs harmonic oscillations.
By studying the swing of a chandelier on a long chain, Galileo studied the properties of a mathematical pendulum. He realized that the period of oscillation of a given system does not depend on the amplitude at small angles of deflection.
Oscillation frequency.
Oscillation frequency is the number of oscillations performed per unit of time, for example, 1 s.
The SI unit of frequency is named hertz (Hz) in honor of the German physicist G. Hertz (1857-1894). If the oscillation frequency (v) is 1 Hz, this means that one oscillation occurs every second. The frequency and period of oscillations are related by the relations:
.
cyclic or circular frequency is also used . It is related to the usual frequency v and the oscillation period T by the relations:
.
Cyclic frequency is the number of oscillations completed in 2π seconds.
AC period and frequency
The time during which one complete change in the emf occurs, that is, one cycle of oscillation or one full revolution of the radius vector, is called the period of alternating current oscillation (Figure 1).
Figure 1. Period and amplitude of a sinusoidal oscillation. Period is the time of one oscillation; Amplitude is its greatest instantaneous value.
The period is expressed in seconds and denoted by the letter T.
Smaller units of measurement of period are also used: millisecond (ms) - one thousandth of a second and microsecond (μs) - one millionth of a second.
1 ms = 0.001 sec = 10 -3 sec.
1 μs = 0.001 ms = 0.000001 sec = 10 -6 sec.
The number of complete changes in the emf or the number of revolutions of the radius vector, that is, in other words, the number of complete cycles of oscillations performed by alternating current within one second, is called alternating current oscillation frequency .
Frequency is designated by the letter f and is expressed in cycles per second or hertz.
One thousand hertz is called a kilohertz (kHz), and a million hertz is called a megahertz (MHz). There is also a unit of gigahertz (GHz) equal to one thousand megahertz.
1000 Hz = 10 3 Hz = 1 kHz;
1000 000 Hz = 10 6 Hz = 1000 kHz = 1 MHz;
1000 000 000 Hz = 10 9 Hz = 1000 000 kHz = 1000 MHz = 1 GHz;
The faster the EMF changes, that is, the faster the radius vector rotates, the shorter the oscillation period. The faster the radius vector rotates, the higher the frequency. Thus, the frequency and period of alternating current are quantities inversely proportional to each other. The larger one of them, the smaller the other.
The mathematical relationship between the period and frequency of alternating current and voltage is expressed by the formulas
For example, if the current frequency is 50 Hz, then the period will be equal to:
T = 1/f = 1/50 = 0.02 sec.
And vice versa, if it is known that the period of the current is 0.02 sec, (T = 0.02 sec.), then the frequency will be equal to:
f = 1/T=1/0.02 = 100/2 = 50 Hz
The frequency of alternating current used for lighting and industrial purposes is exactly 50 Hz.
Frequencies between 20 and 20,000 Hz are called audio frequencies. Currents in radio station antennas oscillate with frequencies up to 1,500,000,000 Hz or, in other words, up to 1,500 MHz or 1.5 GHz. These high frequencies are called radio frequencies or high frequency vibrations.
Finally, currents in the antennas of radar stations, satellite communication stations, and other special systems (for example, GLANASS, GPS) fluctuate with frequencies of up to 40,000 MHz (40 GHz) and higher.
Formula for a spring pendulum. Task No. 2
The formulas of pendulums have a common part, namely 2p. This quantity is present in two formulas at once, but they differ in the radical expression. If in a problem concerning the period of a spring pendulum the mass of the load is indicated, then it is impossible to avoid calculations with its use, as was the case with the mathematical pendulum. But there is no need to be afraid. This is what the period formula for a spring pendulum looks like:
In it, m is the mass of the load suspended from the spring, k is the spring stiffness coefficient. In the problem, the value of the coefficient can be given. But if in the formula of a mathematical pendulum there is not much to clear up - after all, 2 out of 4 quantities are constants - then a 3rd parameter is added here, which can change. And at the output we have 3 variables: the period (frequency) of oscillations, the spring stiffness coefficient, the mass of the suspended load. The task can be focused on finding any of these parameters. Finding the period again would be too easy, so we'll change the condition a little. Find the spring stiffness coefficient if the time of complete oscillation is 4 seconds and the mass of the spring pendulum is 200 grams.
To solve any physical problem, it would be good to first make a drawing and write formulas. They are here - half the battle. Having written the formula, it is necessary to express the stiffness coefficient. We have it under the root, so let’s square both sides of the equation. To get rid of the fraction, multiply the parts by k. Now let’s leave only the coefficient on the left side of the equation, that is, divide the parts by T^2. In principle, the problem could be made a little more complicated by specifying not the period in numbers, but the frequency. In any case, when calculating and rounding (we agreed to round to the 3rd decimal place), it turns out that k = 0.157 N/m.
Angular (cyclic) frequency of alternating current.
The rotation speed of the radius vector, i.e., the change in the rotation angle within one second, is called the angular (cyclic) frequency of alternating current and is denoted by the Greek letter ? (omega). The angle of rotation of the radius vector at any given moment relative to its initial position is usually measured not in degrees, but in special units - radians.
A radian is the angular value of an arc of a circle, the length of which is equal to the radius of this circle (Figure 2). The entire circle that makes up 360° is equal to 6.28 radians, that is, 2.
Figure 2. Radian.
1rad = 360°/2
Consequently, the end of the radius vector during one period covers a path equal to 6.28 radians (2). Since within one second the radius vector makes a number of revolutions equal to the frequency of the alternating current f, then in one second its end covers a path equal to 6.28 * f radians. This expression characterizing the rotation speed of the radius vector will be the angular frequency of the alternating current - ? .
? = 6.28*f = 2f
AC phase.
The angle of rotation of the radius vector at any given instant relative to its initial position is called the phase of the alternating current . The phase characterizes the magnitude of the EMF (or current) at a given instant or, as they say, the instantaneous value of the EMF, its direction in the circuit and the direction of its change; phase indicates whether the emf is decreasing or increasing.
Figure 3. AC phase.
A full rotation of the radius vector is 360°. With the beginning of a new revolution of the radius vector, the EMF changes in the same order as during the first revolution. Consequently, all phases of the EMF will be repeated in the same order. For example, the phase of the EMF when the radius vector is rotated by an angle of 370° will be the same as when rotated by 10°. In both of these cases, the radius vector occupies the same position, and, therefore, the instantaneous values of the emf will be the same in phase in both of these cases.
DID YOU LIKE THE ARTICLE? SHARE WITH YOUR FRIENDS ON SOCIAL NETWORKS!
Oscillation characteristics
The phase determines the state of the system, namely coordinate, speed, acceleration, energy, etc.
The cyclic frequency characterizes the rate of change in the phase of oscillations.
The initial state of the oscillatory system is characterized by the initial phase
Oscillation amplitude A is the largest displacement from the equilibrium position
Period T is the period of time during which the point performs one complete oscillation.
Oscillation frequency is the number of complete oscillations per unit time t.
Frequency, cyclic frequency and period of oscillation are related as
Pendulum swings
The simplest example of an oscillatory process is a pendulum, a light thread with a weight at the end. Let's deflect it from equilibrium to its extreme position, and then release it (to reduce the influence of friction, the deflection should be much less than the length of the thread).
The load will begin to move to the opposite extreme point. Here its speed will drop to zero, and it will swing in the opposite direction to its initial position. (A real pendulum has friction losses and will not reach the starting point a little, but this small deviation can be neglected).
Rice. 2. Oscillations of the pendulum.
A complete movement that starts from a starting point and continues until the nearest return to it is called an oscillation.
Types of vibrations
Oscillations that occur in closed systems are called free or natural oscillations. Oscillations that occur under the influence of external forces are called forced. There are also self-oscillations (forced automatically).
If we consider oscillations according to changing characteristics (amplitude, frequency, period, etc.), then they can be divided into harmonic, damped, increasing (as well as sawtooth, rectangular, complex).
During free oscillations in real systems, energy losses always occur. Mechanical energy is spent, for example, on performing work to overcome air resistance forces. Under the influence of friction, the amplitude of oscillations decreases, and after some time the oscillations stop. Obviously, the greater the force of resistance to movement, the faster the oscillations stop.
What types of fluctuations are there?
Oscillations are divided into harmonic and anharmonic, as well as periodic and non-periodic. It would be logical to assume that in the case of harmonic oscillations they occur according to some harmonic function. It can be either sine or cosine. In this case, compression-extension and increase-decrease coefficients may also come into play. Oscillations can also be damped. That is, when a certain force acts on the system, which gradually “slows down” the oscillations themselves. In this case, the period becomes shorter, while the oscillation frequency invariably increases. This physical axiom is demonstrated very well by a simple experiment using a pendulum. It can be of a spring type, as well as mathematical. It doesn't matter. By the way, the period of oscillation in such systems will be determined by different formulas. But more on that a little later. Now let's give examples.
Forced vibrations. Resonance
Forced oscillations are undamped. Therefore, it is necessary to replenish energy losses for each oscillation period. To do this, it is necessary to influence the oscillating body with a periodically changing force. Forced vibrations occur with a frequency equal to the frequency of changes in the external force.
The amplitude of forced mechanical vibrations reaches its greatest value if the frequency of the driving force coincides with the frequency of the oscillatory system. This phenomenon is called resonance .
For example, if we periodically pull the cord in time with its own vibrations, we will notice an increase in the amplitude of its vibrations.
Examples of resonance
If you move a wet finger along the edge of a glass, the glass will make ringing sounds. Although it is not noticeable, the finger moves intermittently and transfers energy to the glass in short bursts, causing the glass to vibrate
The walls of the glass also begin to vibrate if a sound wave with a frequency equal to its own is directed at it. If the amplitude becomes very large, the glass may even break. Due to resonance, when F.I. Chaliapin sang, the crystal pendants of the chandeliers trembled (resonated). The occurrence of resonance can also be observed in the bathroom. If you softly sing sounds of different frequencies, a resonance will arise at one of the frequencies.
In musical instruments, the role of resonators is performed by parts of their bodies. A person also has his own resonator - this is the oral cavity, which amplifies the sounds made.
The phenomenon of resonance must be taken into account in practice. In some cases it can be useful, in others it can be harmful. Resonance phenomena can cause irreversible damage in various mechanical systems, such as poorly designed bridges. Thus, in 1905, the Egyptian Bridge in St. Petersburg collapsed when a horse squadron was passing across it, and in 1940, the Tacoma Bridge in the USA collapsed.
The phenomenon of resonance is used when, with the help of a small force, it is necessary to obtain a large increase in the amplitude of vibrations. For example, the heavy tongue of a large bell can be swung by applying a relatively small force with a frequency equal to the natural frequency of the bell.
Oscillations and their amplitude
Repeated movements or processes are called oscillations
.
Depending on the nature, vibrations can be mechanical, electromagnetic, sound, etc. Different types of vibrations are described using the same equations and the same characteristics are used.
Vibrations are called free
(go own), if they occur due to the energy that is received by the oscillatory system once and there are no further external influences on this system.
The simplest type of vibration is harmonic vibration.
Harmonic vibrations
are called such oscillations in which the oscillating quantity changes over time according to the law of sine or cosine.
Let harmonic oscillations of some parameter $s$ occur, then these oscillations can be described using the following equation:
where $A=s_ $ is the amplitude of oscillations; $ _0$ — cyclic (circular) frequency of oscillations; $varphi $ — initial phase of oscillations (phase at $t=0$); $( _0t+varphi )$ is the oscillation phase.
Amplitude is the maximum value of the quantity whose fluctuations are being considered. Since the cosine (like the sine) varies from one to minus one, the value $s$ is within the range $-Ale sle $+A.
Definition and physical meaning
The period of oscillation is the period of time during which a body or system performs one oscillation (necessarily complete). At the same time, you can note the parameter at which the oscillation can be considered complete. The role of such a condition is the return of the body to its original state (to the original coordinate). The analogy with the period of a function is very good. It is a mistake, by the way, to think that it occurs exclusively in ordinary and higher mathematics. As you know, these two sciences are inextricably linked. And the period of functions can be encountered not only when solving trigonometric equations, but also in various sections of physics, namely mechanics, optics and others. When transferring the period of oscillation from mathematics to physics, it must be understood simply as a physical quantity (and not a function), which has a direct dependence on the passing time.