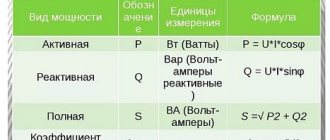
Uniform circular motion is characterized by the period and frequency of revolution.
Circulation period
is the time it takes to complete one revolution.
If, for example, during a time t = 4 s a body, moving in a circle, made n = 2 revolutions, then it is easy to understand that one revolution lasted 2 s. This is the period of circulation. It is designated by the letter T and is determined by the formula:
So,
to find the period of revolution, you need to divide the time during which n revolutions are made by the number of revolutions
.
Another characteristic of uniform circular motion is the rotation frequency.
Frequency
- this is the number of revolutions made in 1 s.
If, for example, in a time t = 2 s the body made n = 10 revolutions, then it is easy to understand that in 1 s it managed to make 5 revolutions. This number expresses the frequency of circulation. It is denoted by the Greek letter V
(read: nu) and is determined by the formula:
So, to find the frequency of revolution, you need to divide the number of revolutions by the time during which they occurred.
The SI unit of revolution frequency is the frequency of revolution at which a body makes one revolution every second. This unit is designated as follows: 1/s or s -1 (read: second minus the first power). This unit used to be called "revolutions per second", but this name is now considered obsolete.
Comparing formulas (6.1) and (6.2), one can notice that period and frequency are mutually inverse quantities. That's why
Formulas (6.1) and (6.3) allow us to find the rotation period T if the number n and the rotation time t or the rotation frequency
V
.
However, it can also be found in the case when none of these quantities are known. Instead, it is enough to know the speed of the body V
and the radius of the circle along which it moves.
To derive a new formula, let us remember that the period of revolution is the time during which the body makes one revolution, that is, it travels a path equal to the length of the circle ( l
en = 2
P
r, where
P
≈3.14 is the number “pi”, known from the mathematics course).
But we know that with uniform motion, time is found by dividing the distance traveled by the speed of movement. Thus, So , to find the period of revolution of a body, you need to divide the length of the circle along which it moves by the speed of its movement.
. 1. What is the circulation period? 2. How can you find the period of revolution, knowing the time and number of revolutions? 3. What is the frequency of circulation? 4. How is the unit of frequency designated? 5. How can you find the frequency of circulation, knowing the time and number of revolutions? 6. How are period and frequency of circulation related? 7. How can you find the period of revolution, knowing the radius of the circle and the speed of the body?
Submitted by readers from Internet sites
A collection of physics lesson notes, abstracts on a topic from the school curriculum. Calendar thematic planning. 8th grade physics online, books and textbooks on physics. The student prepares for the lesson.
If you have corrections or suggestions for this lesson, please write to us.
Rated rotation speed
Before defining this concept, it is necessary to determine what the nominal operating mode of a device is. This is the order of operation of the device in which the greatest efficiency and reliability of the process are achieved over a long period of time. Based on this, the nominal rotation speed is the number of revolutions per minute when operating in nominal mode. The time required for one revolution is 1/v seconds. It is called the rotation period T. This means that the relationship between the rotation period and frequency has the form:
For your information. The rotational speed of the asynchronous motor shaft is 3000 rpm, this is the rated rotation speed of the output shaft shank at the nominal operating mode of the electric motor.
How to find or find out the rotation frequencies of various mechanisms? For this, a device called a tachometer is used.
Uniformly accelerated motion
If over time the position of a body changes relative to objects at rest, then it is considered to be moving. In this case, speed is used as the main parameter describing movement. The movement of a body or point can be represented as a line repeating the path of passage. It's called a trajectory. If the line is straight, then the movement is considered linear.
Uneven movement is characterized by movement along a different trajectory with an inconsistent speed. In this case, the change in position can be uniformly accelerated, that is, the parameter increases or decreases by the same value at equal intervals. An example would be a falling stone.
At an arbitrary point, the speed of movement is equal to the acceleration of gravity.
Thus, if the vectors V and acceleration A lie along a straight line, then in projections this direction can be considered as algebraic quantities. When moving uniformly along a straight path, the speed of a point is calculated by the formula: V = V0 + A*t. Where:
- V0—initial velocity;
- A is acceleration (has a constant value);
- t is the time of movement.
This is a basic formula in physics . On the graph it is depicted as a straight line v (t). The ordinate axis represents time, and the abscissa represents speed. Having constructed a graph, you can determine the acceleration of point A from the slope of the straight line. To do this, use the formula for finding the sides of a triangle: A = (v-v0) / t.
If we select the interval Δt on the time axis, then we can assume that the movement will be uniform and described by some parameter equal to the instantaneous value in the middle of the interval. This instantaneous quantity is a vector quantity. It is numerically equal to the limit that the speed tries to reach in a period of time tending to zero. In physics, this state is described by the instantaneous velocity formula: V = lim (Δ s/ Δ t) = r-1(t). That is, from a mathematical point of view, this is the first derivative.
Based on this, it can be argued that the movement Δs = v*Δt. Since the product of acceleration and time is determined by the difference V -V0, the correct entry will be: S = V0*t + A*t2/2 = (V2 - V20) /2*A.
From this formula we can derive an expression for finding the final velocity of a material point: V = (V20 - 2* A * s)½. If at the initial moment V0 = 0, then the formula can be simplified to the form: V = (2* A * s)½.
Angular velocity
When a body moves in a circle, not all its points move at the same speed relative to the axis of rotation. If we take the blades of an ordinary household fan that rotate around a shaft, then the point located closer to the shaft has a rotation speed greater than the marked point on the edge of the blade. This means they have different linear rotation speeds. At the same time, the angular velocity of all points is the same.
Angular velocity is the change in angle per unit time, not distance. It is denoted by the letter of the Greek alphabet – ω and has a unit of measure: radians per second (rad/s). In other words, angular velocity is a vector tied to the axis of rotation of the object.
The formula for calculating the relationship between rotation angle and time interval is:
Where:
- ω – angular velocity (rad/s);
- ∆ϕ – change in the angle of deflection when turning (rad.);
- ∆t – time spent on deviation ©.
The designation of angular velocity is used when studying the laws of rotation. It is used to describe the motion of all rotating bodies.
Angular velocity in specific cases
In practice, they rarely work with angular velocity values. It is needed in the design development of rotating mechanisms: gearboxes, gearboxes, etc.
You can calculate it using the formula. To do this, use the connection between angular velocity and rotational speed.
Speed concept
When we compare the movement of any bodies, we say that some bodies move faster, while others move slower.
We use such simple terminology in everyday life, talking, for example, about traffic. In physics, the speed of movement of bodies is characterized by a certain value. This quantity is called speed. General definition of speed (if the body moves uniformly): Definition 1
Velocity during uniform motion of a body is a physical quantity that shows how far the body has traveled per unit time.
By uniform motion of a body it is meant that the speed of the body is constant. The formula for finding speed: $v=\frac{s}{t}$, $s$ is the distance traveled by the body (that is, the length of the line), $t$ is the time (that is, the time period during which the path was traveled).
Are you an expert in this subject area? We invite you to become the author of the Directory Working Conditions
According to the international SI system, the unit of linear speed is derived from two basic units - the meter and the second, that is, it is measured in meters per second (m/s). This means that the unit of speed is the speed of such uniform motion that a body travels a distance of one meter in one second.
Speed is also often measured in km/h, km/s, cm/s.
Let's look at a simple example of a speed calculation problem.
Example 1
Task. Moving uniformly, the train covers 219 km in 4 hours. Find its speed of movement.
Solution. $v=\frac{219 km}{4 h}=54.75\frac{km}{h}$. Let's convert kilometers into meters and hours into seconds: $54.75\frac{km}{h}=\frac{54750 m}{3600c}\approx 15.2\frac{m}{c}$.
Answer. $54.75\frac{km}{h}$ or $15.2\frac{m}{c}$.
From the example we see that the numerical value of the speed differs depending on the selected unit of measurement.
In addition to the numerical value, speed has a direction. The numerical value of a quantity in physics is called the modulus. When a physical quantity also has a direction, then this quantity is called a vector quantity. That is, speed is a vector physical quantity.
Finished works on a similar topic
Course work Formula for calculating linear speed 460 ₽ Abstract Formula for calculating linear speed 230 ₽ Test paper Formula for calculating linear speed 250 ₽
Receive completed work or specialist advice on your educational project Find out the cost
In writing, the velocity module is denoted by $v$, and the velocity vector by $\vec v$.
In turn, such quantities as path, time, length and others are characterized only by a numerical value. Then they say that these are scalar physical quantities.
In the case when the movement is uneven, the concept of average speed is used. Average speed formula: $v_{avg}=\frac{s}{t}$, where $s$ is the entire path traveled by the body, $t$ is the entire time of movement. Let's look at an example of a medium speed problem to understand the difference.
Example 2
Task. Some vehicles cover a distance of 213 km in 2.5 hours. Find it $v_{avg}$.
Solution. $v_{avg}=\frac{213 km}{2.5 h}= 85.2 \frac{km}{h}=\frac{213000 m}{9000 s}\approx 23.7\frac{m }{c} $.
Answer. $85.2\frac{km}{h}$ or $23.7\frac{m}{s}$.
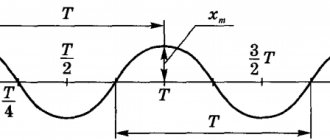
Rotation angle and period of revolution
Consider point A on an object rotating around its axis. When circulating over a certain period of time, it will change its position on the circle line by a certain angle. This is the rotation angle. It is measured in radians, because the unit is a segment of a circle equal to the radius. Another value for measuring the angle of rotation is a degree.
When, as a result of the rotation, point A returns to its original place, it means that it has completed a full rotation. If its movement is repeated n times, then we speak of a certain number of revolutions. Based on this, you can consider ½, ¼ turn and so on. A striking practical example of this is the path that a cutter takes when milling a part fixed in the center of the machine spindle.
Attention! The rotation angle has a direction. It is negative when the rotation occurs clockwise and positive when it rotates counterclockwise.
If a body moves uniformly around a circle, we can talk about a constant angular velocity during movement, ω = const.
In this case, the following characteristics are used:
- period of revolution – T, this is the time required for a full revolution of a point in a circular motion;
- circulation frequency – ν, this is the total number of revolutions that a point makes along a circular path in a unit time interval.
Interesting. According to known data, Jupiter revolves around the Sun every 12 years. When the Earth makes almost 12 revolutions around the Sun during this time. The exact value of the round giant's orbital period is 11.86 Earth years.
Linear velocity and centripetal acceleration
Velocity is a vector quantity. This means that the body receives acceleration not only when the magnitude of v changes, but also when its direction changes. The latter situation occurs during rotation. The instantaneous velocity vector of a body is always directed tangentially to the circle. If in equal intervals of time a body describes equal angles relative to the center of rotation, then such motion is uniform from the point of view of the velocity modulus.
Deviation from straight-line motion during rotation occurs due to the action of a centripetal force, causing centripetal acceleration. It is always directed perpendicular to the speed, so its modulus cannot change. Centripetal acceleration ac can be calculated using the formula:
ac = v2/r.
The absolute value of the acceleration ac shows how strong the centrifugal forces associated with the inertia of the rotating body are. A practical example is a car skidding during a sharp turn. Note that with decreasing radius ac increases more slowly than with increasing linear velocity.
Transition from angular to linear velocity
There is a difference between the linear velocity of a point and the angular velocity. When comparing the quantities in the expressions describing the rules of rotation, you can see the commonality between these two concepts. Any point B belonging to a circle with radius R makes a path equal to 2*π*R. At the same time, it makes one revolution. Considering that the time required for this is the period T, the modular value of the linear velocity of point B is found by the following action:
ν = 2*π*R / Т = 2*π*R* ν.
Since ω = 2*π*ν, it turns out:
Consequently, the linear speed of point B is greater, the further away the point is from the center of rotation.
For your information. If we consider cities at the latitude of St. Petersburg as such a point, their linear speed relative to the earth’s axis is 233 m/s. For objects on the equator – 465 m/s.
The numerical value of the acceleration vector of point B, moving uniformly, is expressed through R and angular velocity, thus:
a = ν2/ R, substituting here ν = ω* R, we get: a = ν2/ R = ω2* R.
This means that the larger the radius of the circle along which point B moves, the greater the value of its acceleration in absolute value. The farther a point of a rigid body is located from the axis of rotation, the greater the acceleration it has.
Therefore, it is possible to calculate accelerations, velocity modules of the required points of bodies and their positions at any time.
Understanding and ability to use calculations and not get confused in definitions will help in practice to calculate linear and angular velocities, as well as freely move from one quantity to another when making calculations.
Uniform movement in a straight line
This is an idealized type of motion, which assumes that a body moves along a straight line in space for a certain period of time. In this case, the speed of the body does not change. Denoting the distance traveled by the symbol l, we obtain the formula:
l = v*t.
Here v = const.
This type of movement was considered by the philosophers of Ancient Greece. They believed that for the movement of bodies it is necessary to apply some force, therefore the natural state of all surrounding objects is rest. Only with the advent of the Renaissance, thanks to the work of Galileo and Newton, it was shown that if a body is not affected by external forces, then the uniformity and straightness of its movement is not disturbed.
Average speed formulas
The average velocity vector ($\left\langle \overline{v}\right\rangle $) when moving between two points is defined as:
\[\left\langle \overline{v}\right\rangle \left(t,t+\Delta t\right)=\frac{\Delta \overline{r}}{\left|\Delta \overline{r} \right|}\frac{\left|\Delta \overline{r}\right|}{\Delta t}=\frac{\Delta \overline{r}}{\Delta t}\left(10\right) ,\]
where in parentheses next to the average speed vector the time interval for which the average speed was found is indicated; $\Delta \overline{r}$ — point displacement vector; $\Delta t$ is the time of movement.
With uneven movement, the average speed for different periods of time is not the same. As $\Delta t$ tends to zero, we find that the average speed tends to the instantaneous speed.
Sometimes when calculating the average speed (it is called the average ground speed), another formula is used:
\[\left\langle v\right\rangle =\frac{s}{t}\left(11\right),\]
where $s$ is the entire path traveled by the point; $t$ is the entire time of its movement. In this case, the average speed is a scalar.
Throwing an Apple: Newton's Law of Universal Gravitation
To conduct experiments with rotational motion, it is not necessary to tie balls to strings and rotate them around you. For example, the Moon does not need any filaments at all to revolve around the Earth. But the fact is that the necessary centripetal force, instead of the tension force of the thread, is provided by the force of gravitational attraction.
One of the most important laws of physics, namely the law of universal gravitation, was derived by Sir Isaac Newton. According to this law, any two bodies are attracted to each other with some force. The magnitude of this attractive force between bodies with masses \( m_1 \) and \( m_2 \), which are at a distance \( r \) from each other, is equal to:
where \( G \) is a constant equal to 6.67·10-11 N·m2/kg2.
Thanks to this equation, you can easily calculate the force of gravitational attraction between two bodies. For example, what is the strength of gravitational attraction between the Earth and the Sun? The Sun has a mass of about 1.99·1030 kg, the Earth - 5.97·1024 kg, and the distance between them is 1.50·1011 m. Substituting these numbers into Newton's law of universal gravitation, we obtain:
Historical apple tree
As you know, an apple fell on Isaac Newton's head and he discovered the law of universal gravitation. Was this really the case? Is it true that some falling apple gave him the right idea, or at least attracted Newton's attention to this topic? According to recent historical research, it is highly unlikely that it was the fall of an apple on the head of the great scientist that inspired him. Most likely, while looking out the window at falling apples in the garden, he found another example of universal gravity. Historians are still arguing about which tree is “Newton’s apple tree.” Staff at Newton's mother's estate at Woolsthorpe near Grantham in Lincolnshire (UK) claim descendants of Newton's “apple tree” are still preserved in her family garden.
Returning from heaven to sinful earth, let's calculate the force of attraction between two lovers on a park bench. How strong can the force of gravitational attraction between them be if, as soon as they meet, they hug each other more and more tightly? Let's say that they weigh 75 kg and are located at a distance of no more than half a meter. Substituting these values into the formula we already know, we get:
An insignificant force of a few millionths of a newton!
We calculate the force of gravitational attraction on the surface of the Earth
The equation described above \( F=(Gm_1m_2)/r^2 \) for the force of gravitational attraction is valid regardless of the distance between two massive bodies. In everyday situations, we often have to deal with small (compared to the size of the Earth) objects on the Earth's surface, i.e. at a fixed distance between the center of the Earth and the center of a small object. The force of gravitational attraction (or gravity) acting on a small object is often called weight. The weight \( F_g \) is equal to the product of the mass \( m \) and the acceleration of gravity \( g \), i.e. \( F_g = mg \). Mass is measured in grams, kilograms, centners, carats, etc., and weight is measured in dynes, newtons and even pound-force.
Let's try to calculate the acceleration of gravity on the surface of the Earth using the law of universal gravitation. We know the formula for the weight of a body with mass \( m_1 \):
It is created by the force of gravitational attraction between this body and the Earth and is equal to this force:
Here \( r \) is the radius of the Earth, equal to 6.38·106 m, and \( m_2 \) is its mass, equal to 5.97·1024 kg.
Reducing body mass \( m_1 \) in both halves of the previous equality, we obtain:
Substituting numerical values, we get:
Thus, thanks to Newton’s law of universal gravitation, we were able to calculate the value of the acceleration of gravity, already known to us from previous chapters. As you can see, for this we needed the values of the universal gravitation constant \( G \), the radius of the Earth \( r \) and its mass \( m_2 \). (Of course, the value of the gravitational acceleration \( g \) can be determined experimentally by measuring the time an object falls from a known height. But, you see, it is much more interesting to use the last formula, for the application of which you will need to experimentally measure... the radius and mass of the Earth. Just kidding! )
We study orbital motion using the law of universal gravitation
Celestial bodies in outer space, due to the force of gravitational attraction, rotate relative to each other: satellites around their planets (like the Moon around the Earth), planets around stars (like the Earth around the Sun in the Solar System), and stars around the center of the Galaxy. (like the Sun - around the center of our galaxy, i.e. the Milky Way), and the Galaxy - around the local group of galaxies (like the Milky Way - around our Local group of galaxies). In all these cases, the bodies are held by the centripetal force provided by the force of gravity. As shown below, this centripetal force is somewhat different from what we know from the previous example of a golf ball spinning on a string. The following sections discuss the well-known laws of rotation of bodies under the influence of gravitational attraction, the so-called Kepler's laws, i.e. relationships between the parameters of rotational motion: periods of rotation, radii and areas of orbits of rotation.
Calculating the speed of the satellite
What is the speed of a satellite revolving around a planet in an orbit with a constant radius? It can be easily determined by equating the centripetal force:
and the force of gravity:
As a result we get:
After simple algebraic operations we obtain the following expression for the rotation speed:
This equation determines the speed of rotation of a satellite in a constant orbit, regardless of its origin, be it an artificial satellite of the Earth, like a man-made spacecraft in a constant orbit, or a natural satellite of the Earth, like the Moon.
Let's calculate the rotation speed of an artificial Earth satellite orbiting the Earth. To do this, you need to substitute the mass of the Earth and the distance from the space orbital satellite to the center of the Earth into the previous formula.
Man-made satellites of the Earth usually rotate at an altitude of about 640 km, and the radius of the Earth is known to be 6.38 106 m. We can assume that artificial satellites rotate in a circular orbit with a radius of about 7.02 106 m. Substituting this and others the numerical values known to us into the previous formula, we get:
There are a few important points to make at this point.
The value of 7.02·106 m in the denominator indicates the distance from the satellite to the center of the Earth, and not the distance from the satellite to the surface of the Earth, which is 640 km. Remember that in the law of universal gravitation, the distance between bodies means the distance between their centers of mass, and not between their surfaces.
In this example, it is assumed that the spacecraft is high enough and does not experience the influence of the atmosphere, for example, the frictional force from contact with it. Actually this is not true. Even at such a high altitude as 640 km, the spacecraft loses speed due to friction in the rarefied layers of the atmosphere. As a result, its speed decreases, and the ship itself gradually decreases. (More on this below.)
The movement of an artificial satellite around the Earth can be considered as an “eternal” fall. It is “kept” from actually falling only by the fact that the velocity vector is always directed perpendicular to the radius of the circle of rotation. Indeed, it is precisely because of this “eternal” fall that astronauts experience a feeling of weightlessness. The fact is that astronauts and their spacecraft “eternally” fall tangentially to the orbit of rotation around the Earth, but at the same time do not get any closer to the Earth.
For practical purposes, it is often more important to know the orbital period of an artificial satellite rather than its speed. This is necessary, for example, in a situation where it is necessary to determine the moment of contact with a spacecraft.
Calculating the satellite's orbital period
The orbital period of a satellite is the time it takes for it to complete a full cycle of rotational motion in its orbit. If we know the orbital speed of movement \( v \) of the satellite in a circle with radius \( r \) (see the previous section), then we can easily and simply calculate the period of revolution \( T \). During the orbital period, the satellite covers a distance equal to the circumference \( 2\pi r \). This means that the orbital speed \( v \) of the satellite is equal to \( 2\pi r/T \). Equating this relationship and the previously obtained expression for the orbital velocity
where \( m \) is the mass of the Earth, we get:
From here it is easy to obtain the following expression for the satellite’s orbital period:
And at what altitude must a satellite be in order to rotate with the period of rotation of the Earth around its axis equal to 24 hours or 86400 s? This is not an idle question at all. Such satellites do exist and are used to provide continuous communications in the region. Indeed, revolving around the Earth with the same period as the Earth, a satellite in such a geostationary orbit is constantly located above the same point on the Earth’s surface. Several of these satellites form a global positioning system. So, using the previous formula, we calculate the radius of the circle of rotation of a satellite in a stationary orbit:
Substituting numerical values, we get:
Subtracting 4.23·107 m from this value, the value of the Earth’s radius equal to 6.38·106 m, we obtain approximately 3.59·107 m, i.e. about 35900 km. It is at this distance from the Earth that the Global Positioning System satellites rotate.
In practice, satellites in geostationary orbit do lose speed due to interaction with the Earth's magnetic field (more on the magnetic field in later chapters). Therefore, satellites are equipped with small engines to adjust their position in geostationary orbit.
Rotating along a vertical plane
Surely you have seen brave motorcyclists, cyclists or skateboarders spinning inside a circular track located in a vertical plane. Why doesn't gravity tip them over at the highest point, where they are upside down? How fast do they need to move so that the force of gravity does not exceed the centripetal force?
Let us consider this situation in more detail using the diagram in Fig. 7.4. For simplicity, let's assume that instead of brave athletes, a small ball moves in a circle located in a vertical plane. So, the previous question is formulated as follows: “What minimum speed must the ball have in order to complete a full cycle of movement along a vertical circle?” What basic condition must the movement of the ball meet in order for it to complete a full cycle of motion along such a circle and not fall at the highest point?
To pass the highest point without falling, the ball must have a minimum speed sufficient to create a centripetal force that would be no less than the force of gravity.
Under such conditions, the normal force from the track will be zero, and the only force that will keep the object on the circle is the force of gravity. Since the centripetal force is equal to:
and the force of gravity is:
then, equating them, we get:
From here we obtain an expression for the minimum required speed for safe movement in a circle located in a vertical plane:
Please note that the minimum required speed for the safe movement of an object in a circle located in a vertical plane is not affected by the mass of the object, be it a ball, a motorcycle or a racing car.
Any object moving at a lower speed at the highest point of the track will inevitably deviate from the circular trajectory and fall. Let's calculate the minimum required speed for safe movement in a circle with a radius of 20 m. Substituting the numerical values into the previous formula, we get:
So, for safe movement in a circle with a radius of 20 m, an object (a ball, a motorcycle or a racing car) must have a speed of at least 14 m/s, i.e. about 50 km/h.
Please note that for safe movement in a circle, the object must have this minimum speed at the highest point! In order to develop such a speed at the top point, the object at the bottom point needs to have a much greater speed. Indeed, in order to get to the top point, the object will have to overcome the force of gravity for some time with an inevitable loss of speed.
The question arises: what is the minimum speed at the bottom point that an object must have to move safely along such a circle? This question will be answered in detail in Part III of this book, which covers concepts such as “kinetic energy,” “potential energy,” and “the conversion of energy from one form to another.”
Chapter 8. Getting the job done →
← Chapter 6. Harnessing the team: inclined planes and friction
Chapter 7. Moving in orbits
2.9 (58.1%) 21 votes