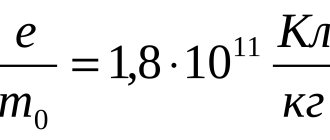Lenz's rule

4.7

Average rating: 4.7

Total ratings received: 267.

4.7

Average rating: 4.7

Total ratings received: 267.

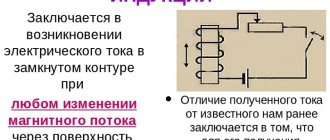
A change in the magnetic field that penetrates the frame with current causes the appearance of an electromotive force (EMF) in it, and a current arises in the frame. The direction of this current is determined by Lenz's special rule for the law of electromagnetic induction. Let's look at this rule.

Lenz's experience

To answer the questions asked, the following experiment is carried out. At the ends of the easily rotating rocker arm, two conductive rings are fixed - one solid and the other with a cut.

Rice. 1. An experiment demonstrating Lenz’s rule.

Now, if you take a permanent magnet and insert it into a ring with a cut, nothing will happen. However, if you try to insert a permanent magnet into a solid ring, the rocker arm will begin to rotate, moving the ring away from the magnet.

This phenomenon can only be explained by the occurrence of current in a solid ring. This current, in turn, generates a new magnetic field, which begins to interact with the field of the permanent magnet. In a ring with a cut, no current arises and there is no interacting field.

The phenomenon of electromagnetic induction

When the current changes, a magnetic field is formed. This phenomenon, in turn, affects the movement of electrons.

If we consider a single wire located straight, it will create a field, the direction of the lines of force of which goes in a circle in a plane perpendicular to it.

If changes occur in the magnetic field, this increases or decreases the strength of the current that passes through the conductor. The direction of change depends on how the field changes. This phenomenon allows you to convert electrical energy into mechanical energy or vice versa.

The scientist credited with discovering the interaction of electric and magnetic fields is Michael Faraday.

Experiments were carried out that showed that a change in the magnetic field can generate the movement of electrons. This phenomenon was later called induced current.

The experiments performed by this scientist are as follows:

Faraday made a coil with a hollow middle. Its ends were connected to a galvanometer. I picked up a magnet and placed it inside the coil. If you push it in or out, the needle on the galvanometer deflects, proving the presence of current. The faster the movement is performed, the greater its strength. A similar effect will be achieved if the magnet is stationary, but the solenoid moves.
In the following experiment two coils were used. The big one is connected to the galvanometer, and the second one is connected to the source. One of the coils was so narrow that it could fit inside the second. If you place it there and turn the current on and off several times, the needle on the galvanometer will deflect, indicating the presence of current.
If you take two solenoids under current and move one of them next to the other, then electron movement will also occur in them.

In such experiments, faster movement creates stronger electron movement.

Joseph Henry carried out similar research simultaneously with Faraday, but published his results later.

Explanation of the phenomenon

The movement of charge carriers - electrons - occurs when they are acted upon by an electromotive force created by a potential difference.

The emergence of a current under the influence of a change in the magnetic field occurs due to the fact that it creates a force called induced emf. Although the phenomenon of inductance was discovered by Faraday, he did not give it a theoretical explanation.

The electromagnetic field theory in physics was created by Maxwell in 1861. This phenomenon has the following features:

the source of electron motion is an alternating magnetic field;
its presence can be detected by the effect it produces on electrical charges;
this field is not potential;
field lines are closed curves.

The work of a magnetic field is expressed in the creation of an electromotive force for electrons.

Carrying out the described experiment, the Russian physicist E. Lenz derived a rule that determines the direction of the induced current in a conducting circuit.

Rice. 2. E. Lenz.

the induced current arising in a closed circuit is directed so as to counteract the cause that causes it.

Applying Lenz's rule to determine the direction of the induced current involves the following steps.

Using the magnetic flux formula $Ф=BScos\alpha$, it is determined how the magnetic flux through the circuit changes - whether it increases or decreases.
The direction of the resulting induction is determined. It, according to Lenz's rule, must be directed in such a way as to counteract the cause that causes it. That is, if the magnetic flux increases, then the resulting induction should be directed against the external induction, if the flux decreases, then along.
The direction of the induction current is determined by the gimlet rule or the rule of reaching the right hand.

Lenz's rule is determined by the law of conservation of energy. Since a current arises in the circuit, it does work (all of it goes to heating the ring), and this work can only arise due to external forces. In Lenz's experiment, such forces are mechanical forces that introduce a magnet into the ring, thereby doing work.

If, for the Lenz experiment, we take a superconducting plate (at very low temperatures) that has no resistance, and place a magnet below, then the induced emf will create a current of such strength that its magnetic field will not allow the plate to approach the magnet, the plate will be able to float in the air, above the magnet without going down.

Rice. 3. Levitation of a superconductor plate above a magnet.

Faraday's law of electromagnetic induction

The main characteristic of a magnetic field is magnetic flux. Visually, it can be represented as lines of force penetrating a perpendicular flat figure bounded by a closed line. These lines express the magnetic induction vector.

The product of the modulus of this quantity and the area for a uniform and homogeneous magnetic field is equal to the field flux through the circuit in question.

When considering a complex field, the figure is divided into small sections in which the field is uniform and the values for each of them are summed up. To calculate in such cases, methods of differential and integral calculus are used.

Electromagnetic induction is measured in Tesla (T). This unit got its name in honor of the great physicist.

Faraday's law

quantitatively describes the effect of a magnetic field on the movement of electrons.
He states the following: the rate of change of the flow of the electromagnetic field is equal to the electromotive force generated by it, acting on the electrons and creating a current.
It should be noted that when a magnetic field is generated by a change in current strength, the resulting electromotive force affects it in the opposite way. This can be made clear with this example.

If a wire is considered and the current in it increases, then this creates a magnetic field. This, in turn, creates an EMF, which prevents the increase.

Self-induction

In this case, we consider a situation where a change in the movement of electrons generates an EMF, causing an induced current in the same conductor.

Taking Lenz's rule as a basis, it can be argued that it has the direction opposite to the initial change.

Self-induction is similar to the phenomenon of inertia. A heavy body cannot be stopped instantly. It is also impossible to change the current strength in one moment to the desired value due to the presence of the phenomenon of self-induction.

This property can be demonstrated by the following experiment. You need to make two electrical circuits. One of them contains a source and a light bulb. The other is made in a similar way, but the difference is that a coil is added to the circuit.

In the first circuit, after switching on, the light comes on immediately. In the second, given the presence of an inductive element, this happens with a noticeable delay.

After opening, the light in the first bulb turns off almost instantly, while in the second it turns off slowly. It is important to note that during the shutdown process the induced current may exceed the initial one. Since in this situation it is directed in the same way as the worker, the current strength may increase. In some circuits this can cause the light bulb to burn out.

Definition and formula

The thermal law can be formulated and written as follows: “The amount of heat generated by the current is directly proportional to the square of the current applied to a given section of the circuit, the resistance of the conductor and the period of time during which electricity acted on the conductor.”

Let us denote by the symbol Q the amount of heat generated, and by the symbols I, R and Δt the current strength, resistance and time period, respectively. Then the formula of the Joule-Lenz law will look like: Q = I 2 *R*Δt

According to Ohm's laws, I=U/R, from which R = U/I. Substituting the expressions into the Joule-Lenz formula we get: Q = U 2 /R * Δt ⇒ Q = U*I*Δt .

The formulas we have derived are different forms of writing the Joule-Lenz law. Knowing parameters such as voltage or current, you can easily calculate the amount of heat generated in a section of the circuit with resistance R.

Differential form

To move on to the differential form of the law, let us analyze the Joule-Lenz statement as applied to electronic theory. The increment in electron energy ΔW due to the work of electric field forces is equal to the difference in electron energies at the end of the path (m/2)*(u=υ max ) 2 and at the beginning of the path (mu 2 )/2 , that is

Here u is the speed of chaotic movement (vector quantity), and υ max is the maximum speed of the electric charge at a given moment in time.

Since it has been established that the speed of chaotic motion coincides with the maximum with equal probability (in the direction and in the opposite direction), then the expression 2* u*υ max is equal to zero on average. Then the total energy released during collisions of electrons with atoms forming nodes of the crystal lattice is:

This is the Joule-Lenz law, written in differential form. Here γ is the matching coefficient, E is the field strength.

Integral form

Let us assume that the conductor has a cylindrical shape with a cross-section S. Let the length of this conductor be l. Then the power P released in the volume V= lS is:

where R is the total resistance of the conductor.

Considering that U = I×R, from the last formula we have:

P = U×I;
P = I2R;
P = U2/R.

If the current value changes over time, then the amount of heat is calculated using the formula:

This expression, as well as the above formulas, which can be rewritten in the same form, is usually called the integral form of the Joule-Lenz law.

The formulas are very convenient for calculating the current power in heating elements. If the resistance of such an element is known, then knowing the voltage of the household network it is easy to determine the power of the device, for example, an electric kettle or a soldering iron.

Vortex electric field

Let us consider a stationary circuit located in an alternating magnetic field. What is the mechanism for the occurrence of induction current in the circuit? Namely, what forces cause the movement of free charges, what is the nature of these external forces?

Trying to answer these questions, the great English physicist Maxwell discovered a fundamental property of nature: a magnetic field changing over time generates an electric field

. It is this electric field that acts on free charges, causing an induced current.

The lines of the resulting electric field turn out to be closed, and therefore it was called a vortex electric field

. The vortex electric field lines go around the magnetic field lines and are directed as follows.

Let the magnetic field increase. If there is a conducting circuit in it, then the induced current will flow in accordance with Lenz’s rule - clockwise, if viewed from the end of the vector. This means that the force acting from the vortex electric field on the positive free charges of the circuit is also directed there; This means that the vector of the vortex electric field intensity is directed exactly there.

So, the lines of intensity of the vortex electric field are directed in this case clockwise (looking from the end of the vector , (Fig. 7).

Rice. 7. Vortex electric field with increasing magnetic field

On the contrary, if the magnetic field decreases, then the lines of intensity of the vortex electric field are directed counterclockwise (Fig. 8).

Rice. 8. Vortex electric field with decreasing magnetic field

Now we can better understand the phenomenon of electromagnetic induction. Its essence lies precisely in the fact that an alternating magnetic field generates a vortex electric field. This effect does not depend on whether a closed conducting circuit is present in the magnetic field or not; With the help of a circuit we only detect this phenomenon by observing the induced current.

The vortex electric field differs in some properties from the electric fields already known to us: the electrostatic field and the stationary field of charges that form a direct current.

1. The vortex field lines are closed, while the electrostatic and stationary field lines begin on positive charges and end on negative ones. 2. The vortex field is nonpotential: its work on moving a charge along a closed loop is not zero. Otherwise, the vortex field could not create an electric current! At the same time, as we know, electrostatic and stationary fields are potential.

So, induced emf in a stationary circuit is the work of a vortex electric field to move a unit positive charge around the circuit

Let, for example, the circuit be a ring of radius and penetrated by a uniform alternating magnetic field. Then the intensity of the vortex electric field is the same at all points of the ring. The work force with which the vortex field acts on the charge is equal to:

Therefore, for the induced emf we obtain:

Application of electromagnetic induction

This phenomenon is actively used in various spheres of human society.

Below are some of the most famous examples:

radio broadcasting is impossible without using the phenomenon of electromagnetic induction;
in medicine, magnetic therapy is one of the effective treatment methods;
in fundamental research, synchrophasotrons are used to accelerate elementary particles, the operation of which is based on the phenomenon of inductance;
electricity meters used in everyday life to account for electricity use the phenomenon under consideration;
in order to transmit electrical energy produced by power plants over long distances, transformers are used, the operation of which is based on the use of electromagnetic induction;
In metallurgy, induction furnaces are used to melt metal.

The use of this phenomenon is very widespread. The examples given are just a sampling of the various use cases.

All formulas on the topic “Electromagnetic induction”

In order to briefly refresh your memory of the formulas related to magnetic induction, the following is a list of the most important of them.

The discovery of the laws that describe the behavior of the electromagnetic field is one of the most important scientific achievements in history. In modern life, the use of this phenomenon occurs in almost all areas of society.