Automatic control is the control of technological processes using advanced devices with predetermined algorithms.
In everyday life, for example, automatic regulation can be carried out using a thermostat, which measures and maintains the room temperature at a given level.
Automatic regulation
We recommend that you pay attention to other devices for regulating technological processes.
Once the desired temperature is set, the thermostat automatically monitors the room temperature and turns the heater or air conditioner on or off as needed to maintain the set temperature.
In production, process control is usually carried out by means of instrumentation and automation, which measure and maintain at the required level the technological parameters of the process, such as temperature, pressure, level and flow. Manual regulation in more or less large-scale production is difficult for a number of reasons, and many processes cannot be adjusted manually at all.
Technological processes and process variables
For the normal implementation of technological processes, it is necessary to control the physical conditions of their occurrence. Physical parameters such as temperature, pressure, level and flow can change for many reasons, and their changes affect the process. These changeable physical conditions are called “process variables.”
Some of them may reduce production efficiency and increase production costs. The goal of an automatic control system is to minimize production losses and control costs associated with arbitrary changes in process variables.
In any production, raw materials and other initial components are affected to obtain the target product. The efficiency and economy of any production depends on how technological processes and process variables are controlled through special control systems.
In a coal-fired thermal power plant, coal is ground and then burned to produce the heat needed to convert water into steam. Steam can be used for a variety of purposes: to operate steam turbines, heat treat, or dry raw materials. The series of operations that these materials and substances undergo is called a “process”. The word process is also often used to refer to individual operations. For example, the operation of grinding coal or turning water into steam might be called a process.
Theory and principles of automation
Initially, the concept of automatic control developed as one of the branches of technical mechanics. In particular, specialists in this area developed principles for controlling electrical machines and steam boilers, but without going beyond the scope of electrical engineering. As the theory of automatic control systems developed, it began to define the functional organs of the working structure as full-fledged objects that influence the production process. Thus, a whole community of interrelated management processes, contained in one dynamic model, was identified. At the present stage of development, theorists of automatic systems are studying the principles of their construction, as well as the patterns of processes occurring inside ready-made models. The quality of work, accuracy and flexibility in terms of adapting systems are influenced by factors such as operating conditions, purpose of the device, design features, etc.
Operating principle and elements of the automatic control system
In the case of an automatic control system, observation and regulation are carried out automatically using pre-configured instruments. The equipment is able to perform all actions faster and more accurately than in the case of manual control.
The action of the system can be divided into two parts: the system detects a change in the value of the process variable and then makes a corrective action that forces the process variable to return to the set value.
An automatic control system contains four main elements: a primary element, a measuring element, a regulating element and a final element.
Elements of the automatic control system
The primary element perceives the value of the process variable and turns it into a physical quantity, which is transmitted to the measuring element. The measuring element converts the physical change produced by the primary element into a signal representing the magnitude of the process variable.
The output signal from the measuring element is sent to the control element. The control element compares the signal from the measuring element with a reference signal, which represents the set value, and calculates the difference between these two signals. The control element then produces a correction signal, which is the difference between the actual value of the process variable and its set value.
The output signal from the control element is sent to the final control element. The final control element converts the signal it receives into a corrective action that forces the process variable to return to the set value.
In addition to the four main elements, process control systems may have auxiliary equipment that provides information about the magnitude of the process variable. This equipment may include instruments such as recorders, meters and alarm devices.
Diagram of a simple automatic control system
1.3. Basic laws of control
If we return to the last figure (block diagram of the ACS in Fig. 1.2.3), then it is necessary to “decipher” the role played by the amplification-converting device (what functions it performs).
If an amplification-converting device (ACD) only amplify (or attenuate) the mismatch signal ε(t), namely: , where is the proportionality coefficient (in the particular case = Const), then such a control mode of a closed-loop ACS is called a proportional control mode (P -control).
If the control unit generates an output signal ε1(t), proportional to the error ε(t) and the integral of ε(t), i.e. , then this control mode is called proportional-integrating (PI control). ==> , where b
– proportionality coefficient (in the particular case
b = Const
).
Typically, PI control is used to improve control (regulation) accuracy.
If the control unit generates an output signal ε1(t), proportional to the error ε(t) and its derivative, then this mode is called proportional-differentiating (PD control): ==>
Typically, the use of PD control increases the performance of the ACS
If the control unit generates an output signal ε1(t), proportional to the error ε(t), its derivative, and the integral of the error ==>, then this control mode is called proportional-integral-differentiating control mode (PID control).
PID control often allows you to provide “good” control accuracy with “good” speed
Types of automatic control systems
There are two main types of automatic control systems: closed and open, which differ in their characteristics and, therefore, in the appropriateness of application.
Closed-loop automatic control system
In a closed system, information about the value of the controlled process variable passes through the entire chain of instruments and devices designed to control and regulate this variable. Thus, in a closed system, a constant measurement of the controlled value is carried out, it is compared with the set value and an appropriate influence is exerted on the process to bring the controlled value into correspondence with the set value.
Scheme of a closed automatic control system
For example, such a system is well suited for monitoring and maintaining the required level of liquid in a tank. The displacer senses changes in the liquid level. The measuring transducer converts the level changes into a signal, which it sends to the regulator. Which, in turn, compares the received signal with the required level specified in advance. Afterwards, the regulator generates a correction signal and sends it to the control valve, which adjusts the water flow.
Open-loop automatic control system
In an open-loop system, there is no closed chain of measuring and signal-processing instruments and devices from the output to the input of the process, and the influence of the controller on the process does not depend on the resulting value of the controlled variable. There is no comparison between the current and desired value of the process variable and no corrective action is generated.
Diagram of an open-loop automatic control system
One example of an open-loop control system is an automatic car wash. This is a technological process for washing cars and all necessary operations are clearly defined. When a car comes out of the wash it is supposed to be clean. If the car is not clean enough, the system does not detect this. There is no element here that would provide information about this and correct the process.
In manufacturing, some open-loop systems use timers to ensure that a series of sequential operations are completed. This type of open-loop control may be acceptable if the process is not very critical. However, if the process requires that certain conditions be verified and adjustments made if necessary, an open-loop system is not acceptable. In such situations, it is necessary to use a closed system.
Construction of automation systems
In the process of developing control systems based on automation, a central place is given to the creation of a functional structure algorithm. At the first stage of construction, the necessary initial data are collected, including the properties of the controlled object, control tasks, the nature of external influences, requirements for control accuracy, etc.
Next, the technical and operational qualities of the automatic systems control controller are studied. The design of this part as a central functional organ resembles a technical actuator that will communicate commands to the controlled object. This infrastructure closes the chain of working elements of the system, the properties of which are determined once at the beginning and can change individual values also within specified ranges. This is the basis of the principle of the unchangeable structure of the management system. It remains unchanged in the sense that its characteristics are established before the direct construction of the control algorithm.
Automatic control methods
Automatic control systems can be built using two basic control methods: closed-loop control, which works by correcting deviations in a process variable after they have occurred; and with disturbance action, which prevents the occurrence of deviations in the process variable.
Feedback control
Closed-loop control is a method of automatic control in which the measured value of a process variable is compared with its pick-up setpoint and action is taken to correct any deviation of the variable from the setpoint.
Manual control system with feedback
The main disadvantage of a closed-loop control system is that it does not begin to regulate the process until the controlled process variable deviates from its set point value.
The temperature must change before the control system begins to open or close the control valve on the steam line. In most control systems, this type of control action is acceptable and is built into the system design.
In some industrial processes, such as drug manufacturing, the process variable cannot be allowed to deviate from the setpoint value. Any deviation may result in loss of product. In this case, a regulatory system is needed that would anticipate changes in the process. This proactive type of regulation is provided by a disturbance-driven control system.
Disturbance control
Disturbance-driven control is proactive control because it predicts the expected change in the controlled variable and takes action before that change occurs.
This is the fundamental difference between disturbance control and feedback control. A disturbance control loop attempts to neutralize the disturbance before it affects the manipulated variable, while a feedback control loop attempts to handle the disturbance after it affects the manipulated variable.
Disturbance control system
A disturbance control system has an obvious advantage over a feedback control system. When controlling by disturbance, in the ideal case, the value of the controlled variable does not change, it remains at the value of its setting. But manual disturbance control requires a more sophisticated understanding of the effect that disturbance will have on the controlled variable, as well as the use of more complex and accurate instruments.
It is rare to find a pure disturbance control system in a plant. When a disturbance control system is used, it is usually combined with a feedback control system. Even so, disturbance control is intended only for more critical operations that require very precise control.
Automatic control
in technology, a set of actions aimed at maintaining or improving the functioning of a controlled object without direct human participation in accordance with a given control goal.
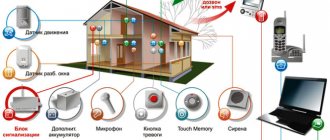
A.u. widely used in many technical and biotechnical systems to perform operations that cannot be carried out by humans due to the need to process a large amount of information in a limited time, to increase labor productivity, quality and accuracy of regulation, freeing humans from managing systems operating in conditions of relative inaccessibility or dangerous for health (see Automation of production, Automation of management work, Large system).
The purpose of control is in one way or another associated with the change in time of the regulated (controlled) quantity - the output quantity of the controlled object. To achieve the control goal, taking into account the characteristics of controlled objects of various natures and the specifics of individual classes of systems, an influence on the control bodies of the object is organized - a control action. It is also intended to compensate for the effect of external disturbing influences that tend to disrupt the required behavior of the controlled variable. The control action is generated by the control device (CD). The combination of interacting control device and controlled object forms an automatic control system.
Automatic control system
(ACS) supports or improves the functioning of the managed object. In some cases, auxiliary operations for self-propelled guns (starting, stopping, monitoring, adjustment, etc.) can also be automated. The self-propelled gun operates mainly as part of a production or some other complex.
The history of technology includes many early examples of designs that have all the distinctive features of an automatic control system (regulation of grain flow in a mill with the so-called “shake”, water level in the steam boiler of Polzunov’s machine, 1765, etc.). The first closed-loop self-propelled control system to receive widespread technical use was an automatic control system with a centrifugal regulator in Watt's steam engine (1784). As steam engines, turbines, and internal combustion engines improved, various mechanical control systems and devices were increasingly used, which reached significant development in the late 19th and early 20th centuries. A new stage in A.u. characterized by the introduction of electronic elements and devices of automation and telemechanics into regulation and control systems. This led to the emergence of high-precision tracking and guidance systems, telecontrol and telemeasurement, and automatic control and correction systems. 50s 20th century were marked by the emergence of complex control systems for production processes and industrial complexes based on electronic control computers.
ACS are classified mainly by control purpose, type of control loop and method of signal transmission. Initially, the ACS was tasked with maintaining certain laws of change in time of controlled quantities. In this class of systems, a distinction is made between automatic control systems (CAP), the task of which is to maintain constant the value of the controlled variable; program control systems, where the controlled quantity changes according to a given program; tracking systems for which the control program is unknown in advance. Subsequently, the management goal began to be associated directly with certain complex quality indicators characterizing the system (its productivity, reproduction accuracy, etc.); the quality indicator may be subject to requirements to achieve its maximum (maximum or minimum) values, for which adaptive or self-adapting systems have been developed.
The latter differ in the control method: in
self-tuning systems,
the parameters of the control device are changed until optimal or close to optimal values of the controlled quantities are achieved;
in self-organizing systems,
its structure can also change for the same purpose.
In principle, the broadest possibilities are for self-learning systems that
improve
algorithms
based on analysis of management experience. Finding the optimal mode in adaptive self-propelled guns can be carried out either using automatic search or in a non-search manner.
The method of compensating for disturbances is related to the type of control loop of the system. In open-loop automatic control systems, the control unit does not receive signals carrying information about the current state of the controlled object, or the main disturbances are measured and compensated for, or control is carried out according to a rigid program, without analyzing any factors during operation. The main type of ACS is closed, in which regulation is carried out by deviation, and the signal flow chain forms a closed loop, including the control object and the control unit; deviations of the controlled value from the desired values are compensated by action through feedback, regardless of the reasons that caused these deviations. Combining the principles of control by deviation and by disturbance leads to combined systems. Often, in addition to the main control loop closed by the main feedback, the ACS has auxiliary loops (multi-loop systems) for stabilization and correction of dynamic properties. Simultaneous control of several quantities influencing each other is carried out in multi-connection control or regulation systems.
According to the form of signal presentation, discrete and continuous automatic control systems are distinguished. In the first, signals, at least at one point in the transmission chain, are quantized in time (see Pulse system
), either by level (see
Relay system
), or by both level and time (see
Signal quantization
).
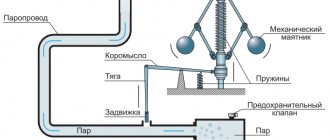
The simplest example of an automatic control system is a system for direct control of engine speed ( Fig. 1
).
The purpose of control is to maintain a constant speed of rotation of the flywheel, the controlled object is engine 1
;
control action - position of the throttle control valve 3
;
УУ is a centrifugal regulator 2,
the coupling
4
of which is displaced under the action of centrifugal forces when it deviates from the set value of the rotation speed of the shaft
5,
rigidly connected to the flywheel.
As the clutch moves, the position of the throttle valve changes. The structural diagram of the considered example ( Fig. 2
) is typical for many automatic control systems, regardless of their physical nature.
The described system is a closed single-circuit continuous system of automatic control of mechanical action, allowing linearization
during research.
The industry produces universal regulators, including those with derivative and integral actions (see Correction of dynamic properties
),
extreme controllers,
for controlling various objects.
Specialized automatic control systems are widely used in various fields of technology, for example: a tracking control system for a copy-milling machine using a hard copy; ACS of metal-cutting machines with program control from magnetic tape, punched tape or punched card (the advantages of such control are relative versatility, ease of program restructuring and high precision of parts processing); a program control system for a reversing rolling mill, which includes a control computer in its circuit. In relatively slow technological processes in the chemical and petroleum industries, multi-connected automatic control systems are common, regulating a large number of related quantities; Thus, during oil distillation, information about temperature, pressure, flow and composition of petroleum products, obtained from several hundred sensors, is used to generate control signals for dozens of different regulators. ACS play an important role in aviation and astronautics, for example, an autopilot is an ACS of associated regulation, and sometimes a self-adjusting system. Military technology uses high-precision tracking systems, often including computing devices (for example, a radar angular tracking system). When analyzing many physiological processes in a living organism, such as blood circulation, regulation of body temperature in warm-blooded animals, and motor operations, characteristic features of self-propelled guns are revealed (see Biological cybernetics
).
Problems of synthesis of A.U. devices. and analysis of processes in controlled systems are the subject of automatic control theory.
R. S. Rutman
Automatic control theory
(TAU) studies the principles of constructing automatic control systems and the patterns of processes occurring in them, which it studies on dynamic models of actual systems, taking into account operating conditions, the specific purpose and design features of the controlled object and automatic devices, in order to build efficient and accurate control systems.
Initially, TAU developed as the theory of automatic control (TAR) and was one of the branches of theoretical and technical mechanics. At this stage, TAU studied the control processes of steam boilers and electrical machines, but separately within the limits of only heating engineering and only electrical engineering. The rapid development of all branches of technology and industry was accompanied by the improvement of methods and means of control technology; the similarity of control processes in technical devices was discovered, regardless of their nature and purpose. With the development of management in technology, there was also a study of management problems in organisms and in economic systems. Until the middle of the 20th century. studies of control processes in these disparate objects were not connected. In technology, control devices external to objects are created separately and only then connected to the objects into a single control system. Based on the study of the interaction of these devices with objects, the commonality of control processes was identified. That is why TAR originated in technology and turned into an independent technical science. In living organisms and in the economy, controls form an integral part of these objects. There is no need to construct separately operating control bodies, and the study of the entire control mechanism was carried out separately in the relevant fields of knowledge without the participation of management specialists. However, management processes, which have certain specifics in biology and economics, required the mandatory collective work of specialists in various fields of science and technology, especially at the current level of development of science, when the need for mutual exchange of knowledge has also emerged. N. Wiener
belonged to the idea of the commonality of control processes in technology, living organisms and economics and the need for joint activities of scientists of various specialties (see
Cybernetics
).
This conclusion has been prepared for a long time and by many other researchers. It was discovered that technical science - TAR - is capable of explaining management processes and influencing them not only in technology; the scope of its application expanded, but at the same time the goals and methods of the theory became more complex, which received the new name “Theory of Automatic Control”. TAR is characterized by the task of stabilizing a given state of an object. In TAU, this task is an integral part of the problem of adaptation, or adaptation, which is inherent in living organisms and economic organizations. But these problems are also very relevant for technology, if we take into account the variability of the parameters of control objects, their operation under changing conditions, as well as the assessment of the effectiveness of this work in purely economic terms, for example, profitability or a reduction in labor and materials costs. This is how the problem of synthesis and analysis of automatic control systems arose - the main problem of TAU. Solving it requires studying the dynamic properties of the ACS, which requires a mathematical description of the behavior of all elements of the system in transient processes. In the general case, processes in objects are described by systems of ordinary differential equations or partial differential equations, depending on whether the objects have lumped or distributed parameters. Elements of automatic devices are also described by systems of differential equations. Specific to TAU is the subsequent transition from linear equations to transfer functions—operator expressions of differential and difference equations. Transfer functions make it easy to present a mathematical model of a system in the form of a block diagram consisting of typical dynamic links. TAU introduces the concepts of dynamic characteristics - transfer functions, frequency and time characteristics, which simplify the compilation of mathematical models of the system and subsequent analysis and synthesis of systems. Dynamic analysis of automatic control systems determines their performance and accuracy. A necessary condition for the operation of automatic control systems is their stability (see Stability
of the automatic control system).
To study it, stability criteria have been developed that make it possible to determine the conditions of stability and the necessary reserves of it based on indirect signs, bypassing the very difficult operation of integrating the equations of motion of the system. Stability is achieved by changing the parameters of the system and its structure. In nonlinear automatic control systems, the self-oscillation mode possible for these systems is investigated .
If, according to the very principle of operation of the ACS, for example for relay systems, these oscillations are inevitable, then acceptable parameters are established - the amplitude and frequency of self-oscillations.
The accuracy of the automatic control system is assessed by indicators that are collectively called the quality of control (see Accuracy
of automatic control systems). The most important indicators of the quality of the automatic control system are: static and dynamic errors and control time (see
Error
in the automatic control system).
These indicators are determined by comparing the actual transient process of change in controlled quantities with the required law of their change; usually they are indicated for one of the standard laws of change of the controlled quantity. In TAU, as well as in stability analysis, they use indirect methods of quality analysis that do not require solving the original equations. For this purpose, quality criteria are introduced - indirect assessments of quality indicators (see Quality indicators
of an automatic control system).
When random disturbances are applied to an automatic control system, the most common criterion for the quality of dynamic accuracy is the mean square error. This value can be relatively simply related to the statistical characteristics of disturbing influences and the parameters of the transfer function of the system. An automatic control system in which the extremum of any quality indicator has been reached is called an optimal system.
Nonlinear systems have greater opportunities to achieve the optimum of a certain quality indicator than linear systems.
This led to the use of nonlinear relationships to improve the quality of control systems. Analysis of a control system establishes the properties of a system with an already given structure. The construction of a control algorithm and the development of a corresponding system structure that fulfills a given goal with the required quality of control, establishing the values of the parameters of this system constitute the content of the synthesis problem. Before the development of a control system begins, the necessary initial data are communicated: the properties of the controlled object, the nature of the disturbances acting on it, the purpose of control and the required control accuracy. The control object includes its control body, through which the influence on the object from the control device is transmitted. The known characteristics of the control body immediately determine the characteristics of the actuator of the control device. But this breaks the chain of parts of the control system, the properties of which are determined uniquely by their mutual influence on each other. This introduces the concept of an unchangeable part of the control system - unchangeable in the sense that its properties are specified before the construction of the control algorithm begins and, as a rule, cannot be changed. The given control goal also determines the control method. As a result, the block diagram of the control system is revealed in general terms. They mainly use two methods for solving the synthesis problem: analytical and successive approximations. In the first, either the type of transfer function of the automatic device or the control algorithm is found, or with the selected structure of the specified device, the values of its parameters are established that give an extremum to the quality criterion. This method allows you to immediately find the optimal solution, but it often leads to complex, cumbersome calculations. In the second method, based on a given quality criterion, the transfer function of an automatic device is determined and then, for the resulting system, the specified quality indicators are compared with their actual values. If the approximation turns out to be acceptable, the calculation is considered complete and the construction of the device can begin. If the approximation turns out to be insufficient, then the type of the transfer function is changed until a variant is obtained that satisfies the specified accuracy requirements. When constructing complex control systems, in addition to theoretical methods, modeling
used using analog and digital computers, on which equations describing the entire control system as a whole are reproduced, and based on the results of calculations, which end when the required quality indicators are achieved, the structure of the control device is established. This synthesis method is close in idea to the method of successive approximations. Modeling makes it possible to evaluate the influence of such factors as nonlinearity of coordinate constraints and variability of parameters, which pose almost insurmountable barriers to analytical research. The use of computers frees you from the difficulties of calculation. They are also used as part of automatic control systems to perform complex control algorithms, which are especially typical for adaptive and optimal systems and systems with prediction of the final control result. The solution to the problem of synthesis of automatic control systems contributed to the emergence of new effective control principles and the development of important independent areas in automatic control systems: optimal control, statistical dynamics and sensitivity of control systems. The theory of optimal control made it possible to establish the structures of control systems that have extremely high quality indicators, taking into account the real restrictions imposed on the variables. Optimality indicators can be very diverse. Their choice depends on the specific task at hand. Such indicators are indicators of the dynamic properties of the entire system as a whole, criteria for the efficiency of modes of controlled objects, etc. Systems that are optimal in terms of performance are widespread, which transfer an object from one state to another in a minimum period of time.
Statistical dynamics of control systems studies the effect of random disturbances on these systems. The methods of this theory make it possible to synthesize control systems that provide a minimum of dynamic error, to solve problems of constructing smoothing and predictive tracking systems, to determine the dynamic properties of controlled objects based on experimental data during their normal functioning without introducing test disturbances. Statistical research methods are widely used to study various types of control systems. These methods are of great importance for adaptive systems. The theory of sensitivity of control systems studies the dependence of the dynamic properties of these systems on their changing parameters and characteristics. The sensitivity index serves as a measure of the dependence of these properties on parameter variations. The theory of sensitivity makes it possible in a number of cases to indicate ways to implement search-free self-adjusting systems.
The last question is closely related to another direction in TAU, which has received intensive development in recent years - the general theory of adaptation, developed on the basis of statistical methods and linear programming methods in mathematics. TAU is characterized by a close, continuously strengthening and mutually influencing connection not only with mathematics, but also with physics and engineering sciences that study the properties of objects, which make it possible to create detailed dynamic models of objects necessary for solving more complex problems of automatic control.
Lit.:
Maxwell D.K., Vyshnegradsky I.A., Stodola A., Theory of automatic control, M., 1949; Lerner A. Ya. Introduction to the theory of automatic control, M., 1958; Feldbaum A. A., Computing devices in automatic systems, M., 1959; him. Fundamentals of the theory of optimal automatic systems, M., 1963; Theory of automatic control, ed. V. V. Solodovnikova, book. 1, M., 1967.
Contents TSB
Single-circuit and multi-circuit control systems
A single-loop control system or simple control loop is a control system with a single loop, which typically contains only one primary sensing element and provides processing of only one input signal to the controller.
Single-circuit control system
Some control systems have two or more primary elements and process more than one input signal per controller. These automatic control systems are called "multi-loop" control systems.
Multi-circuit control system
Automatic control classifications
Control systems of this type mainly differ in the purposes of control, the method of transmitting commands and the types of loop communication. Initially, the tasks were set to support certain laws of measurement. This group includes program control systems, tracking devices and other mechanisms that operate strictly according to certain parameters. Today, with the development of intelligent control principles, the tasks of automatic control systems have become more complex - this can be a whole complex of tasks, for the solution of which not only the data provided by the operator is used, but also dynamic readings derived according to algorithms using values from associated measuring equipment .
Based on the methods of transmitting commands and control in general, self-adjusting, self-organizing and self-learning systems are distinguished. Direct interaction between the components of the control device can be based on analog circuits and modern wireless modules.
Technical support for automatic control
Although the main goal of building automatic controllers is control functionality, even the simplest systems necessarily include measuring and accounting tools. Operating data is supplied to controllers from information sensors, computers and sensors. These are indicators on the basis of which microprocessors, in particular, give commands to actuators. For example, automatic control of technical systems at the physical level can be implemented through electromagnetic devices with shut-off valve elements. Electric motor actuators that control the operation of equipment, units and various equipment have a wider scope.