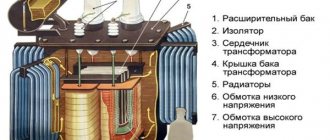
No matter how electronics develops, it is still not possible to abandon such a device as a transformer. Each reliable power supply and voltage converter contains this electromagnetic device with galvanic isolation of the windings. They are widely used both in production and in everyday life, and are a static electromagnetic device that works on the principle of mutual induction. Such devices consist of two main elements:
- closed magnetic circuit;
- two or more windings.
The windings of transformers do not have any connection with each other, except inductive. It is designed to convert only alternating voltage, the frequency of which, after transmission through the magnetic circuit, will be unchanged.
Calculation of the transformer parameters is necessary so that one voltage is supplied to the input of this device, and a reduced or increased voltage of a different specified value is generated at the output. In this case, it is necessary to take into account the currents flowing in all windings, as well as the power of the device, which depends on the connected load and the purpose.
Any even simple calculation of a transformer consists of an electrical and structural component. Electrical part includes:
- Determination of voltages and currents flowing through the windings;
- Determination of transformation ratio.
Structural ones include:
- Core dimensions and device type;
- Choice of transformer core material;
- Possible options for closing housing and ventilation.
Magnetic induction flows through one square centimeter of the cross-section of the magnetic circuit; its unit of measurement is Tesla. Tesla, in turn, is an outstanding physicist, after whom she is named. This value directly depends on the frequency of the current. And so at a frequency of 50 Hz and, say, 400 Hz, the induction (Tesla) values will be different, which means the dimensions of the device decrease with increasing frequency.
After this, the voltage drop and losses in the magnetic circuit are determined; at the stage of electrical calculation, all these values are determined only approximately. Calculation of the load in the transformer is key in its execution. In welding, for example, the load feature is expressed from the short circuit mode. The large value of the short circuit current is associated with the low value of the transformer resistance under these operating conditions.
The most important element of all formulas for this calculation is the transformation ratio, which is defined as the ratio of the number of wound turns in the primary winding to the number of turns in the secondary winding. If there are not two windings, but more, then, accordingly, there will also be several such coefficients. If the winding voltages are known, then it can be calculated as the ratio of the voltages of the primary winding to the secondary.
Calculation of a single-phase transformer
Features of the application and design of welding transformers
When calculating step-down single-phase current transformers, as the most common in everyday life, you first need to find out its power. Of course, you can lower the voltage in other ways, but this is the most effective and also provides galvanic isolation, which means the ability to connect a power load.
For example, if the voltage of the primary winding is 220 Volts, which is typical for standard single-phase current networks, then the secondary voltage must be determined by the load that will be connected to it. This can be either lower or higher voltage. For example, to charge car batteries, a voltage of 12-14 Volts is required. That is, the secondary voltage and current must also be known in advance.
Approximate power will be equal to the product of current and voltage. It is also worth considering efficiency. For power devices it is approximately 0.8–0.85. Then, taking into account this efficiency, the calculated power will be:
Calc = P*efficiency
It is this power that forms the basis for calculating the cross-section of the core on which the windings will be wound. By the way, there can be several types of these magnetic cores, as shown in the figure below.
Next, using this formula we determine the cross section
S (cm2) = (1.0 ÷1.3) √Р
The coefficient 1–1.3 depends on the quality of electrical steel. Electrical steel includes pure iron in the form of sheets or strips 0.1–8 mm thick, or in the form of rolled products (round or square) of various sizes.
After which the number of turns per volt of voltage is determined.
N = (50 ÷70)/S (cm2)
We take the average value of the coefficient 60.
Now knowing the number of turns per volt, it is possible to calculate the number of turns in each winding. All that remains is to find the cross-section of the wire that will be used to wind the windings. Copper is the best material for this, as it has high conductivity and cools quickly when heated. Wire type: PEL or PEV. By the way, heating of even the most ideal electromagnetic device is inevitable, so when manufacturing a network transformer, the issue of ventilation is also relevant. To do this, at least provide a natural ventilated structure on the body by cutting holes.
The current in the winding is
I=P/U
The cross-sectional diameter of the conductor for the winding is determined by the formula:
D= (0.7÷0.9)√I
where 0.7-0.9 is the current density coefficient in the conductor. The higher its value, the less the wire will heat up during operation.
There are many methods for calculating characteristics and parameters, this one is the simplest, but also approximate (imprecise). A more accurate calculation of transformer windings is used for production and industrial needs.
Determining the rated power of a transformer
To correctly select the rated power of a transformer (autotransformer), it is necessary to have a daily load schedule, from which both the maximum and average daily active load of a given substation, as well as the duration of the maximum load, are known.
The graph allows you to judge whether the operating conditions of the load correspond to the theoretical service life (usually 20...25 years) determined by the manufacturer.
For the relative service life of insulation and (or) for the relative wear of insulation, an expression is used that defines exponential dependences on temperature. Relative wear L shows how many times the insulation wear at a given temperature is greater or less than the wear at the nominal temperature. Wear of insulation over time is assessed by the number of hours or days spent: H=Li.
In the general case, when the insulation temperature does not remain constant over time, the wear of the insulation is determined by the integral:
In particular, the average daily wear of insulation:
The influence of insulation temperature determines how many hours the insulation can operate at a given temperature, provided that its wear is equal to the normal wear per day:
At temperatures below 80°C, insulation wear is negligible and can be neglected. The temperature of the cooling medium, as a rule, is not equal to the nominal temperature and, in addition, changes over time. In this regard, to simplify calculations, use the equivalent temperature of the cooling medium, which is understood as such a constant temperature during the calculation period at which the wear of the transformer insulation will be the same as with a changing temperature of the cooling medium in the same period.
It is allowed to take the equivalent temperature for several months or a year equal to the average monthly temperatures or determine the equivalent temperatures using special graphs of the dependence of equivalent monthly temperatures on average monthly and average annual temperatures, equivalent summer (April-August), autumn-winter (September-March) and annual temperatures on average annual temperatures.
If, when choosing the rated power of a transformer at a single-transformer substation, we proceed from the condition
(where Рmax is the maximum active load of the fifth year of operation; Рр is the design rated power of the substation), then with a schedule with a short-term load peak (0.5 ... 1.0 hours), the transformer will operate for a long time with underload. In this case, an overestimation of the rated power of the transformer and, consequently, an overestimation of the installed capacity of the substation is inevitable.
In some cases, it is more profitable to choose the rated power of a transformer close to the maximum load for a sufficient duration with full use of its overload capacity, taking into account systematic overloads in normal mode.
Calculation of a three-phase transformer
Features of the application and selection of measuring current transformers
Manufacturing a three-phase transformer and its precise calculation is a more complex process, since here the primary and secondary windings already consist of three coils. This is a type of power transformer, the magnetic circuit of which is most often made using the rod method. Here such concepts as phase and linear voltages already appear. Linear ones are measured between two phases, and phase ones between a phase and ground. If a three-phase transformer is designed for 0.4 kV, then the linear voltage will be 380V, and the phase voltage 220V. The windings can be connected in a star or triangle, which gives different values of currents and voltages.
The windings of a three-phase transformer are located on the rods in the same way as in a single-phase one, i.e., the low voltage LV windings are placed closer to the rod, and the higher voltage HV windings are located on the lower voltage windings.
High-voltage three-phase current transformers are calculated and manufactured exclusively in industrial conditions. By the way, any step-down transformer, when switched back on, acts as a voltage-increasing device.
Exploitation
When using single-phase transformers, safety precautions are given a special place. This is due to the fact that the device is under high voltage located on the primary windings. When connecting and installing a transformer in electrical circuits, it is important to follow a number of rules to avoid breakdowns and malfunctions of the device:
- To prevent the windings from failing (burning out), it is necessary to install short circuit protection on the secondary circuit;
- It is necessary to control the temperature conditions of the core and windings. It is advisable to install a cooling system that prevents a critical increase in temperature during operation.
In the case of different loads from the electrical network, its voltage also changes. For stable operation of devices receiving energy, it is necessary that the voltage does not change from a set level above the permissible range. In view of this, it is permissible to use methods of voltage regulation in the network.
Calculation of a toroidal transformer
The task and features of grounding transformers.
This design of transformers is used in electronic equipment; they have smaller dimensions, weight, and increased efficiency. Due to the use of a ferrite rod, there is virtually no interference, which makes it possible not to shield these devices.
A simple calculation of a toroidal transformer consists of 5 points:
- Determination of the power of the secondary winding P=Un*In;
- Determination of the overall power of the transformer Pg=P/efficiency. Its efficiency is approximately 90-95%;
- Core cross-sectional area and dimensions
- Determining the number of turns per volt and, accordingly, the number of turns for the required voltage.
- Calculation of the current in each winding and selection of the conductor diameter is done in the same way as in single-phase power transformers described above.
Operating modes
Like any other converter, a single-phase transformer has three operating modes:
- Idle mode. From the name it is clear that no current will flow, due to the open secondary circuit of the device. And an idle current passes through the primary winding, the main element of which is represented by the reactive magnetizing current. The mode is used to determine the efficiency of a transformer, or to display core losses.
- Load mode. The mode is determined by the operation of the transformer with a connected source in the primary circuit, and a certain load in the secondary channel of the device. The secondary circuit is characterized by the flowing load current (calculated from the ratio of the number of turns of the winding and the secondary current) and the no-load current.
- Short circuit mode. The mode operates during the closure of the secondary circuit due to differences in potential values. In this mode, the resulting resistance from the secondary winding will be one load source. When a short circuit occurs, you can calculate the loss due to heating of the winding in the device circuit.
Also read: Three-phase power transformer - TMZ
Calculation of a transformer for a semi-automatic welding machine
The semi-automatic welding machine is designed for welding with mechanical supply of a special welding wire instead of an electrode. The power source of such a device is also based on a powerful transformer. The calculation is based on the principle of its operation, the output of which should be 60 Volts at idle. It operates in short-circuited mode, so heating of its windings is normal. The calculation is also similar in principle, only in this case it is also worth taking into account the power during prolonged welding
Pdl = U2I2 (PR/100)0.5 *0.001.
The voltage and strength of one turn is measured in volts and it will be equal to E=Pdl0.095+0.55. Knowing these values, you can proceed to a full calculation.
General information about transformers
As converters, these devices are traditionally used to bring the power sent along high-voltage lines to an acceptable form. For “transfer” over vast distances, only ultra-high voltages are suitable, at which the current can have an acceptable value.
If you try to transmit energy over at least a hundred kilometers in the form of the usual voltage of 380 Volts, a current of millions of Amperes will be required to deliver the required power to the consumer.
To dissipate it, you need a wire approximately as thick as a human body, which is impossible to implement in practice. Therefore, on the electricity-generating side, with the help of another (step-up) transformer, its value rises to 110 kV. It is impossible to use electricity distribution in residential buildings and production facilities in this form. Therefore, after delivery via HV in distribution stations, 110 kV is reduced to 10(6) kV.
From here they enter the regional transformer substations, where in the local step-down transformer they acquire their final form of 380 (220) Volts. With such potential values, energy can easily be transported via an underground cable or overhead SIP wire to the end consumer. Therefore, a single-phase transformer plays a big role in human life.
Calculation of a pulse transformer of a push-pull converter
The advantage of push-pull converters is their simplicity and the ability to increase power. In a properly designed push-pull converter, a constant current passes through the winding, so there is no strong core bias. This allows you to use a full magnetization reversal cycle and get maximum power. Since it is performed on a ferrite core, the calculation of the output voltage of the transformer is similar to a conventional toroidal one.
You can simplify the transformer calculation options by using special calculation calculators, which are offered by some online resources. One has only to enter the desired data, and the machine will provide the necessary parameters of the planned electromagnetic device.
Main settings
When considering the parameters of voltage and current converters, it is important to note the transformation ratio k, defined as I1/I2 = w2/w1 = 1/k. Here w2 and w1 are the number of turns in the secondary and primary windings, respectively. In addition, such characteristics as the size of the core window in which the coils are placed are also taken into account.
Another parameter characterizing the transfer properties of a single-phase two-winding voltage transformer is the same transformation coefficient k, the value of which for a step-down device is less than 1. And vice versa, if k > 1, this product is a step-up transformer. In the absence of losses in the winding wires and flux dissipation, calculating this indicator is very simple. To do this, it is most convenient to use a simple calculation algorithm: k= U2/U1. If there are several secondary windings, the specified parameter should be determined for each of them separately.
Types of transformers and their applications
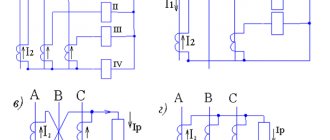
Based on the design features of the core, known samples of single-phase transformers are divided into rod, ring and armored products. According to the shape of the magnetic circuit used in them, they can be:
- W-shaped;
- Toroidal;
- U-shaped.
Each of these forms is suitable for specific purposes related to the need to obtain specified transfer characteristics.
Based on the value of the maximum achievable magnetic coupling (MC), transformers are divided into products with strong, medium and weak interaction. These characteristics largely depend on the design of the product itself and the type of its core.
A single-phase transformer is in demand in areas where it is necessary to coordinate two power circuits with electrical isolation of each of them.
Educational materials
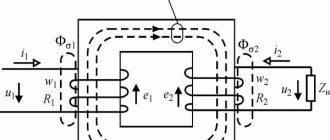
A single-phase transformer has a closed ferromagnetic core, on which primary and secondary windings with the number of turns W1 and W2 are wound.
To reduce eddy currents, the ferromagnetic core is assembled from individual plates of electrical transformer steel with a thickness of 0.35 or 0.5 mm.
In the transformer diagram, conditionally positive directions of all quantities characterizing electromagnetic processes in the transformer are accepted, based on the premise that the primary winding of the transformer is a receiver of electrical energy, and the secondary winding is a source.
Get a decision on TOE
The operation of a transformer is based on the law of electromagnetic induction. When the primary winding is connected to an alternating current source, an alternating current I1 flows in the turns of this winding, which creates an alternating magnetic flux in the core (magnetic circuit). Closing in the core, this flux meshes with the primary and secondary windings and induces in them an emf proportional to the number of turns W:
In the primary winding, self-induction emf
in the secondary winding mutual inductance emf
When the load Zn is connected to the terminals of the secondary winding of the transformer, under the influence of the EMF, current I2 will flow in the winding, and voltage U2 will be established at the terminals.
The transformer winding connected to a network with a higher voltage is called the high voltage winding (HV). The winding connected to the lower voltage network is called the low voltage (LV) winding.
The transformation coefficient K of a transformer is the ratio of the EMF of the HV winding (number of turns Win) to the EMF of the LV winding (number of turns Wnn):
Transformers have the property of reversibility, that is, the same transformer can be used as a step-up and step-down transformer.
A transformer is an alternating current device and does not operate on direct current, since the direct current flowing through the primary winding will create a constant magnetic flux. In accordance with the law of electromagnetic induction, the flux must change both in magnitude and direction.
In the load mode of the transformer, the primary and secondary currents I1, I2, in addition to the main magnetic flux Фо, create magnetic leakage fluxes Фσ1 and Фσ2, the influence of which determines the existence of inductive reactances of the primary and secondary windings of the transformer X1 and X2.
The active and impedance of the primary winding of the transformer are designated R1 and Z1, and the secondary winding - R2 and Z2.
The operation of a transformer is generally described by a system of equations:
where I0 is the no-load current.
Equation (1) and (2) are the equilibrium equations for the EMF of the primary and secondary windings, equation (3) is the equilibrium equation for the magnetizing forces (I⋅W) of the transformer. Magnetizing (magnetomotive) force is the product of current and the number of turns of the winding.
Having performed the transformations in equation (3), we obtain:
From equation (4) it follows that the current I1 of the primary winding of the transformer can be considered consisting of two components: one component I0 determines the main magnetic flux Ф0, and the second component
compensates for the demagnetizing effect of the current I2 of the secondary winding. From the above it follows that the magnetic flux in the transformer does not depend on the load current and is proportional to the applied voltage.
If we neglect the no-load current I0 (a few percent of I1) of the transformer flowing through the primary winding (with the secondary winding open), then we can consider the currents in the windings of the transformer to be inversely proportional to the number of turns.
The following operating modes of the transformer are possible:
- idle mode;
- short circuit mode (emergency mode and short circuit experience);
- load mode.
In no-load mode, the transformer operates with the secondary winding open.
In this case, the following relationships exist:
I2 = 0; I1 = I0 (no-load current); U2 = E2
The no-load power P0 consumed by the transformer from the network is determined mainly by losses in the steel core PC.
P0≈Pc (is 1-2% of rated power)
Losses in steel consist of losses due to magnetization reversal of the ferromagnetic material of the core and losses due to eddy currents, which are induced in the core in accordance with the law of electromagnetic induction. To reduce eddy current losses, the core is made of thin plates (0.3-0.5 mm), insulated from each other.
The no-load test of the transformer is carried out to determine the transformation coefficient K and the power of electrical losses in the steel core.
A transformer short circuit experiment is carried out to determine the power of electrical losses in the transformer windings (copper losses Рм). When conducting a short circuit experiment, the secondary winding of the transformer is short-circuited, while a reduced voltage U1K, amounting to 5-10% of the rated voltage, is supplied to the primary winding. During the experiment, the currents in the windings of the transformer are monitored and the experiment is stopped when the currents in the windings reach nominal values.
The passport data of the transformer includes the no-load current as a percentage of the rated value, the power losses in the windings and the voltage in the short circuit experience, expressed as a percentage of the rated value.
The load mode of a transformer is the mode of its operation when the secondary winding is connected to the load resistance Zn.
The power P1 consumed by the transformer from the network in load mode is determined by the formula:
Р1 = Р2 + ΣР = Р2 + Р0 + Рм,
where P2 is load power;
ΣР – total losses of the transformer (in steel and copper).
Transformer efficiency
has a maximum value when losses in the wires of the windings and losses in the steel of the core are equal
Р0=Рм.
The transformer is designed so that ηmax occurs at the most probable load component (0.5 - 0.75) P2nom..
For a transformer operating under load, the secondary voltage U2 differs from the no-load voltage U20 by the amount of the voltage drop across the impedance of its secondary winding
which is called transformer voltage change
For transformers produced by industry, the ΔU value is 6-8% of U2 nom. (secondary rated voltage). It is useful to know that from the short-circuit voltage U1к obtained in the short-circuit experiment, one can judge the deviation of the voltage of the secondary winding of the transformer from its rated value at the rated current (load).
The change in voltage in the transformer depends not only on the current values of the primary and secondary windings I1 and I2, but also on the type of load (reactive, inductive or capacitive).
The external characteristic of the transformer is the dependence of the voltage U2 of the secondary winding on the current I2 flowing through it, U2=f(I2).
Rice. 13. External characteristics of the transformer
The vector diagram of the transformer is constructed based on the equilibrium equations of the EMF of the primary and secondary windings and the equilibrium equation of the magnetizing forces of the transformer (equations 1, 2, 3).
Next > Lectures on TOE >