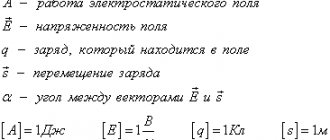Potential difference in electricity: definition, formula for finding

The concept of potential in physics

It is known from a physics course that the work of some forces, for example gravity, does not depend on the trajectory of the body, but depends only on the magnitude of the movement.

Such forces and the force fields in which they act are called potential or conservative.

The force acting on a charge placed in a uniform electrostatic field also refers to potential and is determined by the formula:

Formula 1

F→=q E→,

where q is the electric charge, C;

E→—electric field strength, V.

In mechanics, work is defined as the product of force and the distance between the points - the beginning and end of the movement and the cosine of the angle α between the force and velocity vectors. Similarly, we derive a formula for determining the work of the electrostatic field when moving a charge from one position to another.

Formula 2

A=F→·Δr·cosα=q·E→·Δr·cosα=q·E→·(r2-r1)·cosα=(q·E→·r2-q·E→·r1)·cosα.

The quantity q·E→·r1 is called the potential energy of the field.

Definition 1

Potential energy is a measure of the work done by forces when moving an object in a potential field.

The work depends on the difference in potential energies at the starting and ending points. Then the work can be represented as:

Formula 3

A=-(W2-W1).

Note

The minus sign in the expression for work means that if the potential energy is reduced by force, the work of the field will be positive. If potential energy is increased, the work will be negative.

Let us place a stationary charge q at some point to create an electrostatic field. When charge q1 enters this field, charges q and q1 do not interact with each other; charge q1 is affected by the field itself. To introduce a new characteristic of the field that does not depend on the charges placed in it, it is necessary to divide the potential energy by the charge q. The resulting value is called potential.

Definition 2

Potential (from the word potentia - strength, possibility) is a scalar quantity in physics, equal to the ratio of potential energy to the amount of charge.

In electrics, the following designation for potential is accepted: φ.

Formula 4

φ=Wq.

The potential of an infinitely distant point (r→∞) is considered to be zero.

Current in a circuit always flows from higher potential to lower potential.

The formula for the potential of one charge is given above. In practice, any charged body can be divided into several elements, each of which will have its own potential. Then the potential of a system consisting of two or more charges:

Formula 5

φ=φ1+φ2+φ3+…

Charge around an object

Of course, we can talk about the field if there is any source of it. Each electric body creates a gradient of electric field potential around itself. Compared to gravitational fields, there is an important difference:

Gravitational forces are forces of attraction and can be measured.
The forces of electricity can be either attractive or repulsive.

It is known that field lines refer to the force vectors acting on the body at this point. Scientists agreed that the arrows of the field line will exhibit the reverse vector of the force acting on the negative charge. Consequently, the lines of force “leave” from positive charges and “run” towards negative energy charges.

The concept of potential difference, the formula for finding

Let's substitute the expression for the potential at a point into the formula for work:

Formula 6

A=-(W2-W1)=-(qφ2-qφ1)=-q(φ2-φ1).

A physical quantity, the meaning of which is the difference between the potentials at the initial and final points of the trajectory, is called potential difference or voltage (U).

Formula 7

U=φ1-φ2.

In the simplest case, when only an electrostatic field acts on the circuit or section of the circuit under consideration, the voltage can be considered equal to the potential difference. In other cases, the voltage in a conductor is determined as the sum of the potential difference and the work of external forces (EMF), arising, for example, as a result of the law of electromagnetic induction. Then the voltage:

Formula 8

U=(φ1-φ2)+EMF.

To understand the relationship between voltage and tension, consider a simple capacitor in the form of two plates with a constant capacitance.

An electrostatic field of intensity overrightarrow E is formed between the positively and negatively charged plates. The tension lines between the plates are parallel, and the tension modulus is the same.

If a positive charge is placed next to the positive plate, it will begin to move towards the negative plate, which means that the field will do some work. Since the charge and voltage velocity vectors lie on parallel straight lines, work: A=F→·S.

The length of movement is equal to the distance between the plates, and the force of the field: F→=q·E→.

Then: A=q·E→·Si and A=qU.

Let's equate the expressions for work, we get: q·E→·S=q·U.

Tension and tension are related by the formula:

Formula 9

U=E→·S

Let's place an extended conductor in an electrostatic field. We will assume that the tension lines are horizontal.

Let the conductor move perpendicular to the tension lines. In this case, no work is done to move the charge, since the cosine of the angle between the force and velocity vectors is zero. That is, all points on the surface of the conductor have the same potential.

Definition 3

Equipotential surfaces are surfaces in which the potentials at each point are the same. Equipotential surfaces are a plane for a uniform field and a sphere for a single charge field.

Dielectrics in electrostatics

In addition, guides have another group of bodies - dielectrics . First, you need to clarify the difference between a dielectric and a conductor. Conductors are bodies in which charges can move freely. An example of a conductor is copper wire. If you place a weight on it and then touch it with your hand, the weight will “float” out of the conductor and therefore unload it.

But if glass, which is a dielectric, is positively electrified, then touching it through the hand will not lead to its discharge. Electrons from the limb will only flow at the point of contact, but that glass will still be electrified in the places where it is touched.

Electrons in a dielectric cannot move freely. They are limited to atoms and molecules that they cannot leave. But if you place a dielectric in the field of discharges between a positive and negative charge, this arrangement of electrons and atomic nuclei will change. These particles behave like dipoles. This position shows all the molecules in the dielectric.

A chain of dipoles is formed with charges positive on one side and negative on the other. This phenomenon is called dielectric polarization. A polarized dielectric creates its own field, internal, and its voltage vector is always directed opposite to the field in which the dielectric is located. Thus, the harm from accidents with field voltage is reduced.

Unit of potential difference

Potential equalization box

In honor of the scientist (Alessandro Volta), who first proved the existence of potential differences, the unit of measurement is named Volt. In the international system of units, voltage is indicated by the symbols:

B – in Russian-language literature;
V – in English-language literature.

It will be interesting➡ Circuit inductance

In addition, there are multiple notations:

mV – millivolt (0.001 V);
kV – kilovolt (1000 V);
MV – megavolt (1000 kV).

Conductors in an electrostatic field

Placing a conductor in an electrostatic field causes the field to act on charge carriers inside the conductive object. The carriers begin to move until the electrostatic field outside the surface becomes zero.

Since there is no field inside the substance, the energy will be constant at all points of the conducting material, and the surface will be equipotential. Field strength vectors are directed at right angles at any point on the surface of the conductor.

Under the influence of the field, there are no charges inside the conductor, since they are concentrated exclusively on the surface. This fact is used in shielding - protecting bodies from the influence of external electromagnetic and electrostatic fields. For shielding, not only solid conductive material can be used, but also a mesh, the so-called “Faraday cage”.

Also, the property of moving charged particles (electrons) is used in electrostatic generators to produce voltages of several million volts.

Measuring contact potential difference

The main problem is that the contact potential difference cannot be measured directly with a voltmeter, although the value of the emf in a circuit connecting two different conductors can range from fractions to units of volts.

The contact potential difference significantly affects the current-voltage characteristic of the measured circuit. A good example is a semiconductor diode, where a similar phenomenon occurs at the interface between semiconductors with different types of conductivity.

Conductors in an electrostatic field

Also, the property of moving charged particles (electrons) is used in electrostatic generators to produce voltages of several million volts.

Potential difference in practice

From a generally accepted point of view, potential difference is the voltage between two selected points in the circuit. At the same time, the voltage between each of these points and the third point will differ in full accordance with the definition.

An illustrative example:

Point A in the electrical circuit is a voltage of 10 V relative to the ground wire;
At point B the voltage is 25 V relative to the same wire.

It is necessary to find the voltage between points A and B.

In this case, the required difference is:

UAB= ϕA-ϕB=10-25=15 V.

The concepts discussed are important for a minimum amount of knowledge in the field of electrical engineering and electronics, since all calculations and practical decisions are based on them. Without these basics, a more in-depth study of electrical disciplines is impossible.

Conductors in an electrostatic field. Electrical capacity of a solitary conductor.

If you place a conductor in an external electrostatic field or charge it, then the charges of the conductor will be affected by the electrostatic field, as a result of which they will begin to move. The movement of charges (current) continues until an equilibrium distribution of charges is established, at which the electrostatic field inside the conductor becomes zero. This happens within a very short time. In fact, if the field were not equal to zero, then an ordered movement of charges would arise in the conductor without the expenditure of energy from an external source, which contradicts the law of conservation of energy. So, the field strength at all points inside the conductor is zero:

Gaussian

called the electrical capacitance (or simply capacitance) of a solitary conductor. The capacity of an isolated conductor is determined by the charge, the communication of which to the conductor changes its potential by one.

The capacitance of a conductor depends on its size and shape, but does not depend on the material, state of aggregation, shape and size of cavities inside the conductor. This is due to the fact that excess charges are distributed on the outer surface of the conductor. Capacitance also does not depend on the charge of the conductor or its potential. The above does not contradict the formula, since it only shows that the capacitance of an isolated conductor is directly proportional to its charge and inversely proportional to its potential.

Unit of electrical capacity - farad

(F): 1F

Since electric current is the ordered movement of charged particles, to determine the magnitude of the current it is necessary to know both the energy value of the particles and the force of external influence on them.

Potential. Equipotential surfaces.

In mechanics, the interaction of bodies is characterized by force or potential energy. The electric field, which provides interaction between electrically charged bodies, is also characterized by two quantities. Electric field strength is a force characteristic. Now let’s introduce an energy characteristic—potential. Using this value, it will be possible to compare any points of the electric field with each other. Thus, the potential as a characteristic of the field must depend on the value of the charge contained at these points. Let's divide both sides of the formula A = W1 - W2 by the charge q, we get

The ratio W/q does not depend on the charge value and is taken as an energy characteristic, which is called the field potential at a given point. The potential is designated by the letter φ.

Electric field potential φ is a scalar energy characteristic of the field, which is determined by the ratio of the potential energy W of a positive charge q at a given point in the field to the value of this charge:

The unit of potential is volt:

Like potential energy, the potential value at a given point depends on the choice of the zero level for measuring the potential. Most often in electrodynamics the potential of a point lying at infinity is taken as the zero level, and in electrical engineering - on the surface of the Earth.

With the introduction of potential, the formula for determining the work of moving a charge between points 1 and 2 can be written in the form

Since when a positive charge moves in the direction of the intensity vector, the electric field performs positive work A = q (φ1 - φ2)> 0, then the potential φ1 is greater than the potential φ2. Thus, the electric field strength is directed towards decreasing potential.

If a charge is moved from a certain point in the field to infinity, then the work A = q (φ - φ∞). Since φ∞ = 0, then A = qφ. Thus, the magnitude of the potential φ of a certain point in the field is determined by the work performed by the electric field, moving a unit positive charge from this point to infinity,

If an electric field is created by a point charge q, then at a point located at a distance r from it, the potential is calculated using the formula

Using this formula, the field potential of a charged ball is also calculated. In this case, r is the distance from the center of the ball to the selected point on the field. From this formula it is clear that at equal distances from the point charge that creates the field, the potential is the same. All these points lie on the surface of a sphere described by a radius r around the point charge. Such a sphere is called an equipotential surface.

Equipotential surfaces - the geometric location of points in an electric field that have the same potential - are one of the methods for visually depicting electric fields.

Equipotential surfaces of electric fields created by point charges of different signs

Field lines are always perpendicular to equipotential surfaces. This means that the work done by field forces to move a charge along an equipotential surface is zero.

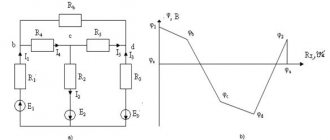
In the case of superposition of electric fields created by several charges, the electric field potential is equal to the algebraic sum of the potentials of the fields created by individual charges, φ = φ1 + φ2 + φ3. The equipotential surfaces of such systems have a complex shape. For example, for a system of two identical charges of the same value, the equipotential surfaces have the form shown in the figure. Equipotential surfaces of a uniform field are planes.

Equipotential surfaces: a - fields of two identical charges b - uniform field

Potential of a system of point charges

Since the electric field is potential, and the principle of superposition operates in it, this makes it easy to find the potential of a system of charges. It is equal to the algebraic sum of elementary charges:

$$\varphi_{general} =\varphi_1+\varphi_2+…+\varphi_n$$

The same formula is used if the charge is distributed unevenly throughout the body. The body is divided into many elementary regions, in each of which the charge can be considered a point charge. After this, the potential of all areas is summed up.

Rice. 3. Potential of the charge system.

What is the electrostatic field potential called?

The electrostatic field potential at a given point is a scalar physical quantity that characterizes the energy properties of the field and is equal to the ratio of the potential energy of an electric charge placed at a given point in the field to the q value of this charge:

It will be interesting➡ Features of using pass-through switches

Unit of potential in Si - volt:

From the definition of potential it follows that the potential ϕ of the field created by a point charge Q at points located at a distance r from a given charge can be calculated using the formula:

From formula (*) it is clear: 1) if the field is created by a positive point charge (Q > 0), then the potential of this field at any point is positive (ϕ > 0); 2) if the field is created by a negative point charge (Q < 0), then the potential of this field at any point is negative (ϕ < 0). Formula (*) is also valid for the field potential of a uniformly charged sphere (or ball) at distances that are greater than its radius or equal to it.

If a field is created by several arbitrarily located charges, the field potential ϕ at any point in a given field is equal to the algebraic sum of the field potentials created by each charge:

How is potential difference determined?

When a charge moves from point 1 to point 2 in an electrostatic field, this field does work that is equal to the change in the potential energy of the charge, taken with the opposite sign: . Since that Expression is called the potential difference, where is the value of the potential at the initial point of the trajectory of the charge, and is the value of the potential at its end point.

Potential difference is a scalar physical quantity equal to the ratio of the work done by the electrostatic field forces to move a charge from the starting point to the final point to the value of this charge:

The unit of potential difference in Si is volt: = 1 V (V).

The potential difference between two points of the field is equal to 1 V if the electrostatic field does 1 J of work to move a charge of 1 C between them. Please note: in such cases, the potential difference is also called voltage (U). It is important not to confuse potential change and potential difference (voltage).

How are the strength of a uniform electrostatic field and potential difference related?

Let's consider a uniform electrostatic field in the area between points 1 and 2, located at a distance d from each other; let charge q move from point 1 to point 2 under the influence of the field (Fig. 42.2).

The work performed by the field can be found in two ways: 1) through the potential difference between points 1 and 2: ; 2) through the field strength: - projection of the vector onto the Ox axis drawn through points 1 and 2.

Equating both expressions for work, we get: , from which: , or

If the charge moves in the direction of the electric field strength ( ), the last formula will take the form:

From the last formula follows the unit of tension in Si - volts per meter:

What surfaces are called equipotential?

To visualize the electrostatic field, in addition to field lines, equipotential surfaces are also used.

An equipotential surface is a surface at all points of which the potential of the electrostatic field has the same value.

For clarity, we should consider not one equipotential surface, but their totality. However, it is difficult to graphically depict a set of surfaces, so usually only the lines of intersection of equipotential surfaces with a certain plane are depicted (Fig. 42.3).

Equipotential surfaces are closely related to the electrostatic field lines. If an electric charge moves along an equipotential surface, then the work done by the field is zero, since A=q ( ), and on the equipotential surface

The work of the electrostatic field can also be represented through the force acting on the charge from the field: AF = scosα, where α is the angle between the vectors and Since A = 0, and F ≠ 0 and s ≠ 0, then cosα = 0, that is, α = 90 °. This means that when a charge moves along an equipotential surface, the force vector and, consequently, the field strength vector at any point are perpendicular to the displacement vector

Thus, the electrostatic field lines are perpendicular to the equipotential surfaces (see Fig. 42.3).

Note! The symmetry of equipotential surfaces repeats the symmetry of field sources. Thus, the field of a point charge is spherically symmetrical, therefore the equipotential surfaces of the field of a point charge are concentric spheres; with a uniform field, equipotential surfaces are a system of parallel planes.

Problem solving

To successfully solve problems related to electric potential, you need not only to know several formulas, but also to understand the essence of the phenomenon. In addition, you often have to use a reference book on electrophysics. For example, to determine the mass of charges.

Here are several typical tasks designed for students to work on independently as part of the school curriculum:

In a conductor, at a distance from each other, there are two point charges q1 = 100 nC and q2 = 10 nC. The distance between them is 10 centimeters. Find their potential energy. To solve the problem, you need to use the fact that the force of interaction between charges is determined by Coulomb’s law: F = k * q / r, where k is a reference value (electric constant). Considering that φ = q / (4 * p * E0 * r), for the case under consideration we can write: E = (q1 * q2) / (4 * p * E0 * r) = (10-7 * 10-8) / (4 * 3.14 * 8.85 * 10-12 * 0.1) = 9 * 10-5 J.
An electric charge moved from point A to B. At the same time, a voltage of 1 kV appeared. The work spent on movement was 40 μJ. Determine the charge value. Using the fact that voltage is a potential difference, found as the ratio of work to energy: Δ φ = A / q, the example can be solved in one action: q = A / U = 400 * 10-6 J / 1 * 103 V = 40 * 10-9 Cl.
A metal sphere with a radius of one meter was placed on the floor. Its charge is 10-6 C. Determine how many times the field potential of a sphere will decrease at a distance of 60 cm from the center of the ball if its radius increases by 3 times. The point being examined is located inside the body. Since in this case the potential of the point in the middle and on the surface is the same, it depends on the radius of the sphere: φ1 = K * q / r. As a result, it will become three times smaller than at the beginning: φ2 = K * q / 3r.
When moving a point charge q = 10 nC from infinity to a point located at a distance r = 10 cm from the surface of the charged sphere, work A = 0.5 μJ was performed. The radius of the sphere is 4 cm. Calculate the surface potential. The solution to the example will look like this: φ = A * (R + r) / q0 * R = 0.5 * 10-6 J * (0.2 m + 0.0 4 m) / 10 * 10-9 C * 0 , 2 m = 3 *102 V = 0.3 kV.

Thus, solving potential problems is simple. But at the same time, it is important to keep track of what the substituted values should be measured in. All calculations are performed in the International System of Units (SI).

Why does an electrician need a potentiometer?

What is power factor

This device is widely used in practice for voltage modulation. The fact is that many sources (especially those designed for autonomous operation: battery cells, solar panels, etc.) have a constant voltage that cannot be controlled without special devices, which can cause problems. To reduce the initial voltage of such an element, divider devices equipped with potentiometers are used.

Potentiometer-rheostat

How does a potentiometer work? It is a resistor with a pair of terminals and a movable slider with another terminal. Such a variable resistance device can be connected in two ways:

Like a rheostat, using a slider lead and one of a couple of others. Resistance is measured by moving the slider along the resistor body. In this case, regulation of the circuit current is possible by connecting such a rheostat and a voltage source in series.
By a potentiometric method, using each output from the device’s trio. Two main terminals are connected in parallel with the source, and the reduced voltage is removed from the slider mechanism and one terminal. In this case, an electric current flows through the resistor device, creating a voltage drop between the slider and the side terminals. In such a model, a large load is placed on the power source, since for the accuracy of regulation and the absence of failures, it is necessary that the resistor resistance be several times lower than the load value.

It will be interesting➡ Twisted pair: categories, crimping, work tips

Potentiometric connection of the device

Thus, the concept of potential is used in different areas of physics: both in mechanics and in the study of electricity. In the latter case, it acts as a characteristic of the field. The quantity under consideration cannot be measured directly, but the difference can be measured, then one charge is taken as the reference point.

Gauss's theorem for magnetic field

Gauss's theorem is one of the most basic laws in electrodynamics. There are Gauss's theorems for electric and magnetic fields, which are part of Maxwell's equations. Using this law, a connection is established between the strength of the electric field and the charge in the case of an arbitrary surface. Gauss's theorem (law) states that in an arbitrary closed surface the flow of the electric field vector is proportional to the charge contained inside the surface. For a magnetic field, Gauss's theorem says that the flux of the magnetic induction vector through an arbitrary closed surface is zero.

Concept of potential, potential difference

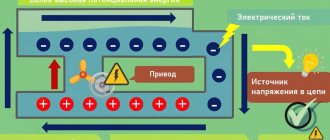
Closely related to the concept of electric current voltage is the concept of “potential”, or “potential difference”. Okay, let's go back to our plumbing analogy.

Our tank is located on a hill, which allows water to flow down the pipe freely. Since the water tank is at a height, the potential of this point will be higher or more positive than that at ground level. Do you see what happens?

We now have two points with different potentials, or rather different potential values.

It turns out that in order for electric current to flow through a wire, the potentials must not be equal. Current runs from a point with a higher potential to a point with a lower potential.

Remember this expression that current runs from plus to minus. So this is all the same. Plus is a more positive potential and minus is more negative.

By the way, do you want a question for backfilling? What will happen to the current if the potentials change places periodically?

Then we will observe how the electric current changes its direction to the opposite each time the potentials change. This will turn out to be alternating current. But we won’t consider it for now, so that a clear understanding of the processes can form in our heads.

Potential drop along a conductor

At the ends of a conductor placed in an electric field, a potential difference begins to be observed. As a result, electrons begin to move towards increasing the difference. An electric current arises in the conductor. Free electrons move along the conductor until the difference is zero. In practice, to maintain a given current value, circuits are powered from voltage or current sources. The difference is this:

The current source maintains constant current in the circuit regardless of the load resistance;
The voltage source maintains a strictly constant EMF at its terminals, regardless of the amount of current consumed.

The potential difference (voltage drop) is proportional to the distance from the ends of the conductor, that is, it has a linear dependence.

The essence of the concept of potential difference

To study the properties of charged particles placed in an electrostatic field, the concept of potential was introduced. It means the ratio of the energy of a charge placed in an electrostatic field to its magnitude.

When a charged particle is transferred to another point in the field, its potential energy changes, but the magnitude of the charge remains unchanged. Transfer requires a certain amount of energy. This energy for transferring a unit of charge is called electrical voltage. Accordingly, a larger supply of energy will accelerate the transfer, that is, the higher the voltage, the greater the current in the circuit.

Potential difference

In this case, the potential difference is numerically equal to the voltage between the points where a unit charge is located. For the general case, the work of external forces must be added here, which is called electromotive force (EMF). At its core, electricity is the work of a third-party source (generator) to maintain specified voltage and current levels in an electrical circuit.

The essence of the concept of potential difference

Conductors in an electrostatic field

Conductor in an electrostatic field

Faraday cage

Also, the property of moving charged particles (electrons) is used in electrostatic generators to produce voltages of several million volts.