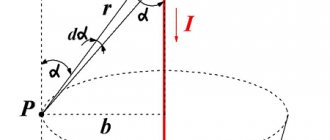
The existence of direct current in the circuit ensures the presence of an EMF source. However, if we have a sufficiently long conductor and it is located at a large distance from the source, the field strength created by the battery charges is relatively small. The source of the emf cannot be a direct source of the field inside the conductor. The only source of constant electric field is exclusively electric charge. Consequently, the question of the sources of the field in a conductor comes down to finding out the type of charges that generate the field in the conductor and their location.
Content
- 1 1. Field inside the conductor
- 2 2. Charge distribution in a conductor
- 3 3. Field outside the conductor near its surface
- 4 4. Potential distribution in a conductor
- 5 5. Cavity inside the conductor
“I want to tell you a new and terrible experience, which I do not advise you to repeat... Suddenly my right hand was struck with such force that my whole body shook, as if from a lightning strike. ...In a word, I thought that the end had come... For the sake of the French crown, I would not agree to once again be subjected to such a terrible shaking...” These are the words from the memoirs of the Leiden professor Muschenbreck, given in the book by V. Kartsev “The Adventures of the Great Equations.” Muschenbrek carried out experiments on electricity in 1745 and obtained the simplest capacitor, later called the Leyden jar. During the experiments, the professor was subjected to “such a terrible shock” as a result of the discharge of a capacitor through the human body, which, as is known, is a conductor.
The fact that conductors exist in nature enriches the world around us with a variety of electrical phenomena, some of which are far from safe. Conductors occupy an important place in the study of electromagnetism.
Let us consider in detail the case when a charged stationary conductor is in an external electrostatic field (created by extraneous stationary charges). In a conductor, sooner or later all charges will stop moving, and equilibrium will occur (since otherwise we would get a perpetual motion machine as a result of the continuous release of heat during the movement of charges). For such a charged conductor placed in an external electrostatic field, the statements given below will be valid.
Properties of conductors
Resistivity
The main characteristics of electrical conductors are:
- resistance,
- electrical conductivity.
When electrons move through a conducting substance, they collide with ions and atoms. This leads to resistance.
If a potential difference is created between two conductors, then an electric current will flow through the third one connecting them. The direction of its movement will be from greater potential to less. In this case, the carriers will be electrons that are not connected to each other, which determine the value of the electrical conductivity of the substance.
Electrical conductivity is the ability of a material to pass electric current. This indicator is inversely proportional to the resistance of the material, measured in siemens, see.
Depending on the charge carriers, electrical conductivity can be:
- electronic,
- ionic,
- hole
Conductor with electronic conductivity
Note! A reliable conductor is characterized by low resistance to the flow of moving electrons and, accordingly, high electrical conductivity. The greatest conductivity is the property of the best conductor.
The selection of conductive materials should be carried out in accordance with their properties:
- Electrical (resistivity and temperature coefficient of resistance);
- Physical (melting degree, density);
- Mechanical (resistance to stretching, bending, machine processing);
- Chemical (interaction with the environment, the possibility of connection during welding, soldering).
Metals without impurities have low resistivity. For alloys this figure increases. Resistance also increases with increasing temperature.
Important! When cooled to critical values, the resistance of most conductive substances drops to zero. This property is called superconductivity.
When choosing conductors for electrical installations, power lines, protective grounding and other applications, it is important to take into account all the qualities of the materials.
Charge distribution in a conductor
In order to answer the question about charge distribution in a conductor, we need to clarify some properties of the electrostatic field lines. Let us recall that the electric field line (including electrostatic) is an imaginary line in space, drawn so that the tangent to it at each point coincides with the vector of the electric field strength at this point. The experience of studying electrostatic fields gives reason to conclude that the lines of force of these fields are continuous and not closed, they can begin only on positive charges and end only on negative ones and cannot begin (end) at a point in space where there are no charges. When graphically depicting the field of a certain system of charges, the number of field lines starting or ending on any charge is proportional to the modulus of this charge. It follows that lines of force necessarily come out of (or enter into) any charge.
After what has been said about lines of force, let us return to the question of charge distribution in a conductor. Let us mentally select an arbitrary sufficiently small volume Δ V
inside the conductor (Fig. 1). Let's assume that this volume has a charge (to be specific, positive). Then lines of force will emerge from the selected volume, i.e., an electric field will exist near it. But there is no field inside the conductor. Therefore, the allocated volume must be neutral. And since we took this volume at an arbitrary place inside the conductor, we can say that the entire “inside” of the conductor is neutral and, therefore, the entire charge of the conductor is on its surface.
Rice. 1
Conductors in an electrostatic field
If you place a conductor in an external electrostatic field or charge it, then the charges of the conductor will be affected by the electrostatic field, as a result of which they will begin to move. The movement of charges (current) continues until an equilibrium distribution of charges is established, at which the electrostatic field inside the conductor becomes zero. This happens within a very short time. In fact, if the field were not equal to zero, then an ordered movement of charges would arise in the conductor without the expenditure of energy from an external source, which contradicts the law of conservation of energy. So, the field strength at all points inside the conductor is zero:
E = 0.
The absence of a field inside a conductor means, according to (85.2), that the potential at all points inside the conductor is constant (j = const), i.e. the surface of the conductor in an electrostatic field is equipotential
(see § 85).
It also follows that the field strength vector on the outer surface of the conductor is directed normal to each point on its surface. If this were not so, then under the action of the tangential component E the charges would begin to move along the surface of the conductor, which, in turn, would contradict the equilibrium distribution of charges. If a conductor is given a certain charge Q, uncompensated charges are located only on the surface
of the conductor.
This follows directly from Gauss’s theorem (89.3), according to which the charge Q located
inside the conductor in a certain volume limited by an arbitrary closed surface is equal to
since at all points inside the surface D = 0.
Let us find the relationship between the Efield strength near the surface of a charged conductor and the surface charge density s on its surface. To do this, we apply Gauss’s theorem to an infinitesimal cylinder with bases DS crossing the conductor-dielectric boundary. The cylinder axis is oriented along vector E (Fig. 141). The flux of the electric displacement vector through the inside of the cylindrical surface is zero, since inside the conductor E1 (and therefore D1) is zero, so the flux of the vector D through the closed cylindrical surface is determined only by the flux through the outer base of the cylinder. According to Gauss's theorem (89.3), this flux (DDS) is equal to the sum of the charges (Q = sDS) covered by the surface: DDS = sDS, i.e.
| or |
(92.1) (92.2)
where s is the dielectric constant of the medium surrounding the conductor.
Rice. 141
Thus, the electrostatic field strength at the surface of the conductor is determined by the surface charge density. It can be shown that relation (92.2) specifies the electrostatic field strength near the surface of a conductor of any shape.
If a neutral conductor is introduced into an external electrostatic field, then free charges (electrons, ions) will move: positive - along the field, negative - against the field (Fig. 142, a). An excess of positive charge will accumulate at one end of the conductor, and an excess of negative charge at the other. These charges are called induced. The process will occur until the field strength inside the conductor becomes equal to zero, and the field strength lines outside the conductor become perpendicular to its surface (Fig. 142, b).
Thus, a neutral conductor introduced into the electrostatic field breaks some of the tension lines; they end at negative induced charges and begin again at positive ones. The induced charges are distributed on the outer surface of the conductor. The phenomenon of redistribution of surface charges on a conductor in an external electrostatic field is called electrostatic induction.
Rice. 142
From Fig. 142, b
it follows that induced charges appear on the conductor due to
displacement
under the influence of the field, i.e. s is the surface density of displaced charges. According to (92.1), the electrical displacement D near the conductor is numerically equal to the surface density of displaced charges. Therefore, vector D is called the electric displacement vector.
Since in a state of equilibrium there are no charges inside the conductor, the creation of a cavity inside it will not affect the configuration of the arrangement of charges and thereby the electrostatic field. Consequently, there will be no field inside the cavity. If now this conductor with the cavity is grounded, then the potential at all points of the cavity will be zero, i.e. the cavity is completely isolated from the influence of external electrostatic fields. This is the basis of electrostatic protection—shielding of bodies, such as measuring instruments, from the influence of external electrostatic fields. Instead of a solid conductor, a dense metal mesh can be used for protection, which, by the way, is effective in the presence of not only constant, but also alternating electric fields.
The property of charges being located on the outer surface of a conductor is used to design electrostatic generators designed to accumulate large charges and achieve a potential difference of several million volts. The electrostatic generator, invented by the American physicist R. Van de Graaf (1901-1967), consists of a spherical hollow conductor 1 (Fig. 143), mounted on insulators 2. A moving closed tape 3 made of rubberized fabric is charged from a voltage source using a system of points 4 ,
connected to one of the poles of the source, the second pole of which is grounded. Grounded plate 5 enhances the flow of charges from the tips onto the tape. Another system of points 6 removes the charges from the tape and transfers them to the hollow ball, and they transfer to its outer surface. Thus, a large charge is gradually transferred to the sphere and a potential difference of several million volts is achieved. Electrostatic generators are used in high-voltage charged particle accelerators, as well as in low-current high-voltage equipment.
Rice. 143
If you place a conductor in an external electrostatic field or charge it, then the charges of the conductor will be affected by the electrostatic field, as a result of which they will begin to move. The movement of charges (current) continues until an equilibrium distribution of charges is established, at which the electrostatic field inside the conductor becomes zero. This happens within a very short time. In fact, if the field were not equal to zero, then an ordered movement of charges would arise in the conductor without the expenditure of energy from an external source, which contradicts the law of conservation of energy. So, the field strength at all points inside the conductor is zero:
E = 0.
The absence of a field inside a conductor means, according to (85.2), that the potential at all points inside the conductor is constant (j = const), i.e. the surface of the conductor in an electrostatic field is equipotential
(see § 85).
It also follows that the field strength vector on the outer surface of the conductor is directed normal to each point on its surface. If this were not so, then under the action of the tangential component E the charges would begin to move along the surface of the conductor, which, in turn, would contradict the equilibrium distribution of charges. If a conductor is given a certain charge Q, uncompensated charges are located only on the surface
of the conductor.
This follows directly from Gauss’s theorem (89.3), according to which the charge Q located
inside the conductor in a certain volume limited by an arbitrary closed surface is equal to
since at all points inside the surface D = 0.
Let us find the relationship between the Efield strength near the surface of a charged conductor and the surface charge density s on its surface. To do this, we apply Gauss’s theorem to an infinitesimal cylinder with bases DS crossing the conductor-dielectric boundary. The cylinder axis is oriented along vector E (Fig. 141). The flux of the electric displacement vector through the inside of the cylindrical surface is zero, since inside the conductor E1 (and therefore D1) is zero, so the flux of the vector D through the closed cylindrical surface is determined only by the flux through the outer base of the cylinder. According to Gauss's theorem (89.3), this flux (DDS) is equal to the sum of the charges (Q = sDS) covered by the surface: DDS = sDS, i.e.
| or |
(92.1) (92.2)
where s is the dielectric constant of the medium surrounding the conductor.
Rice. 141
Thus, the electrostatic field strength at the surface of the conductor is determined by the surface charge density. It can be shown that relation (92.2) specifies the electrostatic field strength near the surface of a conductor of any shape.
If a neutral conductor is introduced into an external electrostatic field, then free charges (electrons, ions) will move: positive - along the field, negative - against the field (Fig. 142, a). An excess of positive charge will accumulate at one end of the conductor, and an excess of negative charge at the other. These charges are called induced. The process will occur until the field strength inside the conductor becomes equal to zero, and the field strength lines outside the conductor become perpendicular to its surface (Fig. 142, b).
Thus, a neutral conductor introduced into the electrostatic field breaks some of the tension lines; they end at negative induced charges and begin again at positive ones. The induced charges are distributed on the outer surface of the conductor. The phenomenon of redistribution of surface charges on a conductor in an external electrostatic field is called electrostatic induction.
Rice. 142
From Fig. 142, b
it follows that induced charges appear on the conductor due to
displacement
under the influence of the field, i.e. s is the surface density of displaced charges. According to (92.1), the electrical displacement D near the conductor is numerically equal to the surface density of displaced charges. Therefore, vector D is called the electric displacement vector.
Since in a state of equilibrium there are no charges inside the conductor, the creation of a cavity inside it will not affect the configuration of the arrangement of charges and thereby the electrostatic field. Consequently, there will be no field inside the cavity. If now this conductor with the cavity is grounded, then the potential at all points of the cavity will be zero, i.e. the cavity is completely isolated from the influence of external electrostatic fields. This is the basis of electrostatic protection—shielding of bodies, such as measuring instruments, from the influence of external electrostatic fields. Instead of a solid conductor, a dense metal mesh can be used for protection, which, by the way, is effective in the presence of not only constant, but also alternating electric fields.
The property of charges being located on the outer surface of a conductor is used to design electrostatic generators designed to accumulate large charges and achieve a potential difference of several million volts. The electrostatic generator, invented by the American physicist R. Van de Graaf (1901-1967), consists of a spherical hollow conductor 1 (Fig. 143), mounted on insulators 2. A moving closed tape 3 made of rubberized fabric is charged from a voltage source using a system of points 4 ,
connected to one of the poles of the source, the second pole of which is grounded. Grounded plate 5 enhances the flow of charges from the tips onto the tape. Another system of points 6 removes the charges from the tape and transfers them to the hollow ball, and they transfer to its outer surface. Thus, a large charge is gradually transferred to the sphere and a potential difference of several million volts is achieved. Electrostatic generators are used in high-voltage charged particle accelerators, as well as in low-current high-voltage equipment.
Rice. 143
Field outside a conductor near its surface
The vector of the electrostatic field strength at any point outside the conductor near its surface is directed perpendicular to the surface, which in other words can be said this way: the field lines enter and exit the conductor at right angles to the surface of the conductor. Otherwise, there would be a component of the field strength vector along the surface of the conductor, and a force with a component along the surface would act on the free charges on the surface of the conductor. As a result, charges would begin to move along the surface of the conductor, which would upset the balance.
Potential distribution in a conductor
Let us show that the potential difference of any two points of a conductor, including points on the surface, is equal to zero. Let there be arbitrary points M
and
K
inside the conductor.
Let us mentally transfer from point M
to point
K
a test charge
q
along a certain trajectory
MVC
lying inside the conductor (Fig. 2).
The field forces will not do work on the moving charge q
, since there is no field inside the conductor.
Therefore, the potential difference φ
M
φ
K = 0. If points
M
and
K
, one or both, lie on the surface of the conductor, then the proof that the potential difference between them is zero is similar.
Rice. 2
Since the potential difference of any two points on a conductor is zero, the potential of all points on the conductor, including points on the surface, is the same. Therefore, they talk about the potential of a conductor without indicating its specific point. Since all points on the surface of a conductor have the same potential, the surface of the conductor will be an equipotential surface.
Electricity
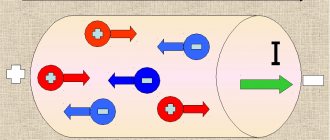
This is the directed movement of charged particles. In metals, current carriers are free electrons, in electrolytes - negative and positive ions, in semiconductors - electrons and holes, in gases - ions and electrons. The quantitative characteristic of current is the current strength.
The sources can be a galvanic cell (chemical reactions occur and internal energy is converted into electrical energy) and a battery (for charging, direct current is passed through it; as a result of a chemical reaction, one electrode becomes positively charged, the other negatively charged.
Actions of electric current
: thermal, chemical, magnetic.
Direction of electric current
: from + to –
Directed movement of charged particles
Therefore, a sufficient condition for the existence of a current is the presence of an electric field and free charge carriers. The presence of current can be judged by the phenomena that accompany it: The conductor through which the current flows heats up. Electric current can change the chemical composition of a conductor.
Force influence on neighboring points and magnetized bodies.
When an electric field exists inside a conductor, a potential difference exists at its ends. If it does not change, then a constant electric current is established in the conductor.
Cavity inside the conductor
Let's remove part of the substance from the inner region of the conductor. Since the substance being removed is neutral, it should be expected that the electrostatic field at all points outside the conductor, inside the conductor and in the resulting cavity will not change. And this will indeed be the case, and there will be no charges on the inner surface of the conductor (on the surface of the cavity). The entire charge of the conductor will be concentrated on the outer surface of the conductor, and the presence of a cavity inside the conductor will not affect the distribution of charge over the outer surface. There will be no field in the cavity or in the conductor. The potential of all points of the conductor and the cavity will be the same.
In short, a hollow conductor that has a charge and is placed in an external electrostatic field behaves in the same way as the corresponding solid one. We will not provide a proof of this statement, but note that it is confirmed by numerous experiments carried out by G. Cavendish (1731-1810) at the end of the 18th century and M. Faraday (1791-1867) at the beginning of the 19th century.