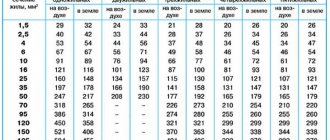
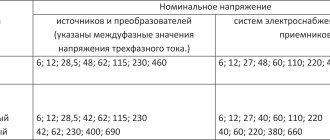
Examples of calculations
Specific examples will provide significant assistance in understanding the principles of calculations and the sequence of actions when performing calculations, which interested visitors should familiarize themselves with.
Calculation of the volume of required coolant
For a country house of temporary residence, you need to calculate the volume of purchased propylene glycol - a coolant that does not solidify at temperatures down to -30°C. The heating system consists of a 60 liter jacketed stove, four aluminum radiators of 8 sections each and 90 meters of PN25 pipe (20 x 3.4).
Pipes of the PN25 20 x 3.4 standard are most often used to organize a small heating circuit with radiators connected in series. Its internal diameter is 13.2 mm
The volume of liquid in the pipe must be calculated in liters. To do this, you need to take the decimeter as a unit of measurement. The formulas for converting from standard length values are as follows: 1 m = 10 dm and 1 mm = 0.01 dm.
The volume of the boiler jacket is known. V1 = 60 l.
The passport of the aluminum radiator Elegance EL 500 indicates that the volume of one section is 0.36 liters. Then V2 = 4 * 8 * 0.36 = 11.5 l.
Let's calculate the total volume of pipes. Their internal diameter d = 20 – 2 * 3.4 = 13.2 mm = 0.132 dm. Length l = 90 m = 900 dm. Hence:
V3 = π * l * d2 / 4 = 3.1415926 * 900 * 0.132 * 0.132 / 4 = 12.3 dm3 = 12.3 l.
Thus, we can now find the total volume:
V = V1 + V2 + V3 = 60 + 11.5 + 12.3 = 83.8 l.
At industrial and agricultural facilities, homemade heating radiators are often installed, arranged like registers. Knowing the dimensions of the pipes, you can calculate their volume
Calculation of the volume of a homemade radiator
Let's look at how to calculate a classic homemade heating radiator made from four horizontal pipes 2 m long. First you need to find the cross-sectional area. You can measure the outer diameter from the end of the product.
Let it be 114 mm. Using the table of standard parameters of steel pipes, we find the wall thickness characteristic of this size - 4.5 mm.
Let's calculate the internal diameter:
d = 114 – 2 * 4.5 = 105 mm.
Let's determine the cross-sectional area:
S = π * d2 / 4 = 8659 mm2.
The total length of all fragments is 8 m (8000 mm). Let's find the volume:
V = l * S = 8000 * 8659 = 69272000 mm3.
The volume of vertical connecting tubes can be calculated in a similar way. But this value can be neglected, since it will be less than 0.1% of the total volume of the heating radiator.
The resulting value is not informative, so let’s convert it to liters. Since 1 dm = 100 mm, then 1 dm3 = 100 * 100 * 100 = 1000000 = 106 mm3.
Therefore V = 69272000 / 106 = 69.3 dm3 = 69.3 l.
Therefore, since it will be necessary to calculate the volume of pipes in m3, then all dimensions will need to be immediately converted into meters before substituting them into the formula.
Selection by table
Knowing the diameter of the wire, you can determine its cross-section using a ready-made dependence table. The table for calculating the cable cross-section by core diameter looks like this:
| Conductor diameter, mm | Conductor cross-section, mm2 |
| 0.8 | 0.5 |
| 1 | 0.75 |
| 1.1 | 1 |
| 1.2 | 1.2 |
| 1.4 | 1.5 |
| 1.6 | 2 |
| 1.8 | 2.5 |
| 2 | 3 |
| 2.3 | 4 |
| 2.5 | 5 |
| 2.8 | 6 |
| 3.2 | 8 |
| 3.6 | 10 |
| 4.5 | 16 |
When the cross-section is known, it is possible to determine the permissible power and current values for copper or aluminum wire. In this way, it will be possible to find out what load parameters the current-carrying core is designed for. To do this, you will need a table of the dependence of the cross section on the maximum current and power.
Converting watts to kilowatts
In order to correctly use the table of wire cross-section versus power, it is important to correctly convert watts to kilowatts.
1 kilowatt = 1000 watts. Accordingly, to obtain the value in kilowatts, the power in watts must be divided by 1000. For example, 4300 W = 4.3 kW.
Cross-sectional area
In general, the cross-sectional area of a complex or composite shape is defined as the sum (sometimes subtracting) of its constituent simple shapes, such as a rectangle, a triangle, and a circle.
Formulas for calculating the area of the main figures.
Example: Calculate the cross-sectional area of a complex shape with a square hole and a curve. To calculate the total area, a complex section is decomposed into simple figures:
Rectangle - 1, triangle - 2, semicircle - 3 and rectangle - 4, the areas of which are simply determined. As a result, the area of the entire cross-section will be obtained by adding the first three figures and subtracting figure number 4:
A=A1+A2+A3-A4
The cross-sectional area is denoted by the Latin letters S or A , and is measured in square units of length, for example: m2, cm2 or mm2.
Composite sectional area
Composite sections are those that consist of two, three or more separate figures that are not one whole. This could be, for example, a section of a beam, consisting, for example, of a channel and two corners.
These sections themselves are also complex. The cross-sectional areas for such standard profiles can be found in a special reference book - assortment.
As a result, adding up all the component profiles, we obtain the area of the entire cross-section.
Thus, the calculation of the area of the composite section is carried out similarly to the previous procedure, only without subtractions.
What is the cross section measured in?
After determining the diameter using the indicated methods, the cross-sectional area can be determined using a formula or a special table. It is measured in square millimeters. This unit of measurement is derived according to the Unified International System of Measurements.
You might be interested in Description of installed and estimated capacity
Unit of measurement
At the same time, the cut of the vein was always round.
How to calculate pipe parameters
When building and furnishing a home, pipes are not always used to transport liquids or gases.
They often act as a building material - to create the frame of various buildings, supports for canopies, etc. When determining the parameters of systems and structures, it is necessary to calculate the various characteristics of its components.
In this case, the process itself is called pipe calculation, and it includes both measurements and calculations.
Why do we need calculations of pipe parameters?
In modern construction, not only steel or galvanized pipes are used. The choice is already quite wide - PVC, polyethylene (HDPE and LDPE), polypropylene, metal-plastic, corrugated stainless steel.
They are good because they do not have as much mass as their steel counterparts. However, when transporting polymer products in large volumes, it is advisable to know their weight in order to understand what kind of machine is needed.
The weight of metal pipes is even more important - delivery is calculated by tonnage. So it is advisable to control this parameter.
What cannot be measured can be calculated
It is necessary to know the outer surface area of the pipe to purchase paint and thermal insulation materials. Only steel products are painted, because they are susceptible to corrosion, unlike polymer ones. So you have to protect the surface from exposure to aggressive environments.
They are used more often for the construction of fences, frames for outbuildings (garages, sheds, gazebos, cabins), so the operating conditions are difficult, protection is necessary, therefore all frames require painting.
This is where the area of the surface to be painted is required - the outer area of the pipe.
When constructing a water supply system for a private house or cottage, pipes are laid from the water source (well or borehole) to the house - underground.
And still, to keep them from freezing, insulation is required. You can calculate the amount of insulation by knowing the outer surface area of the pipeline.
Only in this case it is necessary to take material with a substantial margin - the joints must overlap with a substantial margin.
The cross-section of the pipe is necessary to determine the throughput - whether this product can carry the required amount of liquid or gas. The same parameter is often needed when choosing the diameter of pipes for heating and plumbing, calculating pump performance, etc.
Inner and outer diameter, wall thickness, radius
Pipes are a specific product. They have an internal and external diameter, since their wall is thick, its thickness depends on the type of pipe and the material from which it is made. Technical specifications often indicate the outer diameter and wall thickness.
Pipe inner and outer diameter, wall thickness
Having these two values, it is easy to calculate the internal diameter - subtract twice the wall thickness from the external one: d = D - 2*S. If you have an outer diameter of 32 mm, a wall thickness of 3 mm, then the inner diameter will be: 32 mm - 2 * 3 mm = 26 mm.
If, on the contrary, there is an internal diameter and wall thickness, but an external one is needed, we add double the stack thickness to the existing value.
With radii (denoted by the letter R) it is even simpler - this is half the diameter: R = 1/2 D. For example, let’s find the radius of a pipe with a diameter of 32 mm. Just divide 32 by two, we get 16 mm.
Vernier caliper measurements are more accurate
What to do if there are no technical data for the pipe? To measure. If special accuracy is not needed, a regular ruler will do; for more accurate measurements, it is better to use a caliper.
Calculation of pipe surface area
The pipe is a very long cylinder, and the surface area of the pipe is calculated as the area of the cylinder. For calculations, you will need a radius (internal or external - depends on what kind of surface you need to calculate) and the length of the segment that you need.
Formula for calculating the side surface of a pipe
To find the lateral area of the cylinder, we multiply the radius and length, multiply the resulting value by two, and then by the number “Pi”, we obtain the desired value. If desired, you can calculate the surface of one meter, which can then be multiplied by the desired length.
For example, let’s calculate the outer surface of a piece of pipe 5 meters long, with a diameter of 12 cm. First, let’s calculate the diameter: divide the diameter by 2, we get 6 cm.
Now all quantities must be reduced to the same units of measurement. Since the area is calculated in square meters, we convert centimeters to meters. 6 cm = 0.06 m.
Next, we substitute everything into the formula: S = 2 * 3.14 * 0.06 * 5 = 1.884 m2. If you round it up, you get 1.9 m2.
Weight calculation
When calculating the weight of a pipe, everything is simple: you need to know how much a linear meter weighs, then multiply this value by the length in meters.
The weight of round steel pipes is in reference books, since this type of rolled metal is standardized. The weight of one linear meter depends on the diameter and wall thickness.
One point: the standard weight is given for steel with a density of 7.85 g/cm2 - this is the type recommended by GOST.
Round Steel Pipe Weight Table
In table D - outer diameter, nominal diameter - inner diameter, And one more important point: the weight of ordinary rolled steel is indicated; galvanized steel is 3% heavier.
Weight table for profiled square pipe
How to calculate cross-sectional area
Formula for finding the cross-sectional area of a round pipe
If the pipe is round, the cross-sectional area should be calculated using the formula for the area of a circle: S = π*R2. Where R is the radius (internal), π is 3.14. In total, you need to square the radius and multiply it by 3.14.
For example, the cross-sectional area of a pipe with a diameter of 90 mm. We find the radius - 90 mm / 2 = 45 mm. In centimeters this is 4.5 cm. We square it: 4.5 * 4.5 = 2.025 cm2, substitute it into the formula S = 2 * 20.25 cm2 = 40.5 cm2.
Prism sections
A prism is a large class of figures that are characterized by the presence of two identical polygonal bases parallel to each other, connected by parallelograms. Any cross section of a prism is a polygon. Due to the variety of figures under consideration (oblique, straight, n-gonal, regular, concave prisms), the variety of their sections is also great. Below we will consider only some special cases.
If the cutting plane is parallel to the base, then the cross-sectional area of the prism will be equal to the area of this base.
If the plane passes through the geometric centers of the two bases, that is, it is parallel to the lateral edges of the figure, then a parallelogram is formed in the section. In the case of straight and regular prisms, the type of section under consideration will be a rectangle.