Energy
Let’s go by the principle “the simpler the better.” Among all the definitions of energy, one can highlight:
Energy is one of the basic properties of matter and a measure of the ability to do work.
Energy in classical mechanics is measured in Joules and is most often denoted by the letter E.
And here we smoothly approach the work. Of course, few people like to work; relaxing is much more pleasant. But let’s also read about work.
Types of mechanical energy
In mechanics, there are two types of energy:
- Kinetic. This term refers to the mechanical energy of any body that moves. It is measured by the work that a body could do when braking to a complete stop.
- Potential. This is the combined mechanical energy of an entire system of bodies, which is determined by their location and the nature of the interaction forces.
Accordingly, the answer to the question of how to find mechanical energy is theoretically very simple. It is necessary: first calculate the kinetic energy, then the potential energy and summarize the results obtained. Mechanical energy, which characterizes the interaction of bodies with each other, is a function of relative position and speed.
Job
Work is a measure of the effect of force on a body or system of bodies.
Both work and energy are scalar physical quantities. Like energy, work in classical mechanics is measured in Joules.
Let's say we took a cart with bricks (let it weigh m kilograms), started pushing it with a certain force F and thereby moved all this stuff a distance s .
Then the work that we did (and we definitely did the work, albeit meaningless), will be calculated using the corresponding formula for work in mechanics:
At the same time, while we were pushing the cart, it acquired some speed v , and therefore energy.
The kinetic energy (energy of motion) of the trolley is calculated by the formula:
If we push ourselves and roll our cart up a hill of height h , then it will acquire potential energy, which can also be easily calculated:
By the way! For all our readers there is now a 10% on any type of work .
Work does not happen on its own. Work is done by changing energy. What is the relationship between work and energy?
For example, the work done by gravity is equal in magnitude to the change in the potential energy of the body.
There is a theorem about the kinetic energy of a system . It states that the change in the kinetic energy of the system is equal to the work of all internal and external forces acting on the bodies of the system.
Work and power of electric current
In one of our previous lessons, we talked about how charged bodies interact with each other through a special type of matter called an electric field. An example of such interaction is electric current, that is, the ordered movement of charged particles that is created by an electric field. Consequently, the electric field is capable of doing work, which is called the work of current.
Let's remember that in the general case, work is understood as a scalar physical quantity that describes the action of a force (note, it is a force, not a body), leading to a change in the velocity value of the body in question.
From this it becomes obvious that the term “current work” is a kind of jargon that you have already encountered many times. The work of current is, in the strict language of physics, the work of electrical forces that, by moving charged particles, increase their speed, and therefore kinetic energy.
We already know that the work of transferring an electric charge in an electric field is estimated by multiplying the magnitude of the transferred charge by the magnitude of the potential difference between the initial and final points of the transfer, that is, by the magnitude of the voltage:
A
=
ΔqU
. Obviously, this relationship can also be applied to assess the work of the current. However, this formula has an inconvenience due to the fact that it also includes a charge transferred in an electric field, the measurement of which requires special methods. Therefore, it is more convenient to describe this charge using the current formula:
This notation leads us to a convenient formula for determining the work of electric current: the work of the current in a section of the circuit is equal to the product of the current strength, voltage and time during which the current flowed:
A
=
IU Δ t.
The unit of current work, as you guessed, is the joule. This unit can be expressed in terms of electrical units - ampere and volt:
1 J = 1 A ∙ 1 V ∙ 1 s.
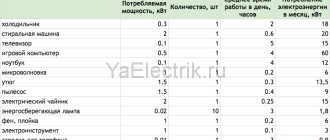
To measure the work of current in real life, they use special devices - electric energy meters, which can now be seen in every home. However, in them the work of current is usually expressed not in joules, but in kilowatt-hours (1 kW ∙ hour = 3.6 ∙ 106 J)
.
Applying Ohm's law to the consumer of electric current, it is possible to obtain two more options from the basic formula of the work, excluding voltage from the formula in the first case, and current strength in the second:
Having obtained the formula for the work of electric current, we can easily obtain the formula for current power. After all, in any case, power is the ratio of work to the time of its completion:
Recall that the unit of measurement for power is the watt.
And to measure the power of electric current in a circuit, special devices called wattmeters are used.
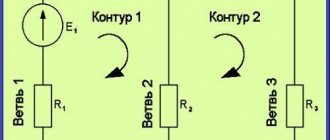
Let's solve this problem with you as an example. Two consumers whose resistances are equal to R
1 and
R
2 are connected to the DC network first in series and then in parallel. In what case is more power consumed from the network?
In one of the previous lessons, we talked about the effects of electric current that it can exert when flowing in various environments. Let us remember that the thermal effect of current
manifests itself in the fact that when current flows through the conductor, the latter heats up.
Chemical effect of current
we can observe it as it passes through solutions of salts, acids or alkalis.
And the magnetic effect of current
manifests itself in the creation of a magnetic field.
We also talked about the fact that current produces thermal effects in any medium: solid, liquid and gaseous. For example, heating of a conductor occurs because free charge carriers, electrons, accelerated under the influence of an electric field, collide with ions of the crystal lattice of the conductor and give them part of their energy. As a result, the energy of thermal motion of ions near equilibrium positions increases. That is, the energy of the electric field is converted into the internal energy of the conductor.
At the same time, it is obvious that the greater the resistance of the conductor, the greater the amount of heat released in it when an electric current of the same strength flows.
This can be easily verified by simple experiment. Let's take three series-connected conductors made of different materials, for example, nichrome, nickel and copper, and connect them to a direct current source.
After some time, we will notice that the nichrome conductor heated up to almost white heat, the nickel conductor only turned slightly red, but the copper conductor practically did not change its color.
Thus, indeed, the greater the resistance of the conductor, the “difficult” it is for charges to move in it and the more the conductor heats up.
In 1841, the English scientist James Prescott Joule and, independently of him, in 1842, the Russian scientist Emilius Christianovich Lenz, studying experimentally the thermal effects of current, established a law that allows one to calculate the amount of heat released in a conductor when an electric current flows through it. According to this law, the amount of heat released in a conductor is directly proportional to the square of the current passing through the conductor, the resistance of the conductor and the time during which a constant current in the conductor is maintained.
Let's check its validity with the help of such an experiment. Let's take a calorimeter containing 100 ml milliliters of water at a temperature of 18 ° C, and place a conductor in the form of a spiral of known resistance in it. The ends of the conductor will be connected to a circuit consisting of a current source, an ammeter and a switch. We will use a stopwatch to time the experiment.
Having closed the key, wait until the temperature of the water in the calorimeter increases by 10 °C.
Now let’s calculate the amount of heat received by water, using the formula known to us from thermodynamics:
Here c
is the specific heat capacity of water;
m
is its mass;
and Δt is
the change in water temperature. Then, after substituting numbers and simple calculations, we find that the water received 4200 J of heat from the heater.
Now let’s determine the amount of heat released in the conductor using the Joule-Lenz law:
Substituting the data of our experiments into the resulting equation, we find that during the experiment the same 4200 J of heat were released in the conductor. This confirms the correctness of the Joule-Lenz law.
Formula Q
=
I
2
R
Δ
t
is convenient to use when calculating the amount of heat that is released in conductors during a series connection, since in this case the current in all conductors is the same.
When conductors are connected in parallel, the current in them is different, but the voltage at the ends of these conductors is the same. Therefore, it is more convenient to calculate the amount of heat for such a connection using the formula: Q
=
U
2Δ
t
/
R
.
This formula shows that when connected in parallel, an amount of heat is released in each conductor that is inversely proportional to the resistance of the conductor.
Law of energy conservation
The law of conservation of energy is a fundamental law of nature that should never be forgotten.
The total amount of energy of a closed physical system does not increase or decrease, but passes from one form to another, always remaining constant.
So, if a cart rolls down a hill, its potential energy will turn into kinetic energy. We do not consider friction forces (dissipative forces) here. In the real world, the cart, of course, will slow down, but the energy will not disappear, but will turn into the internal energy of molecules due to the friction of the wheels on the surface.
The law of conservation of energy is applicable not only within the framework of classical mechanics. This is a law that applies to the entire Universe. Here's what Richard Feyman said about the law of conservation of energy:
This is a mathematical principle that states that there is a certain numerical value that does not change under any circumstances. This is by no means a description of the mechanism of the phenomenon or anything specific... It simply notes the strange circumstance that you can count a certain number and then calmly watch how nature will play any of its tricks, and then count this number again - and it will remain the same.
Energy and work
Energy is a measure of the ability of a physical system to do work, so energy and work are quantitatively expressed in the same units (joules, [J]).
Mechanical work is numerically equal to the change in mechanical energy. We can easily feel this connection between work and energy: for example, if you spend the day very actively, then by the evening there will be no strength or energy left.
In mechanics, it is generally accepted that the work of moving a body from one position to another is done by a force. The work of force can be calculated using the formula:
A=F∙s∙cosα,
where F is the force doing the work, [H];
S—body displacement, [m];
α is the angle between the direction of force and the direction of movement.
If the angle α is acute, then the work of force is positive; if it is straight, then the work is zero; if it is obtuse, then the work is negative.
Basic theoretical information
Mechanical work
The energy characteristics of motion are introduced on the basis of the concept of mechanical work or work of force . The work done by a constant force F is a physical quantity equal to the product of the force and displacement modules multiplied by the cosine of the angle between the vectors of force F and displacement S:
How to successfully prepare for the CT in physics and mathematics?
In order to successfully prepare for the CT in physics and mathematics, among other things, it is necessary to fulfill three most important conditions:
- Study all topics and complete all tests and assignments given in the educational materials on this site. To do this, you need nothing at all, namely: devote three to four hours every day to preparing for the CT in physics and mathematics, studying theory and solving problems. The fact is that the CT is an exam where it is not enough just to know physics or mathematics, you also need to be able to quickly and without failures solve a large number of problems on different topics and of varying complexity. The latter can only be learned by solving thousands of problems.
- Learn all the formulas and laws in physics, and formulas and methods in mathematics. In fact, this is also very simple to do; there are only about 200 necessary formulas in physics, and even a little less in mathematics. In each of these subjects there are about a dozen standard methods for solving problems of a basic level of complexity, which can also be learned, and thus, completely automatically and without difficulty solving most of the CT at the right time. After this, you will only have to think about the most difficult tasks.
- Attend all three stages of rehearsal testing in physics and mathematics. Each RT can be visited twice to decide on both options. Again, on the CT, in addition to the ability to quickly and efficiently solve problems, and knowledge of formulas and methods, you must also be able to properly plan time, distribute forces, and most importantly, correctly fill out the answer form, without confusing the numbers of answers and problems, or your own last name. Also, during RT, it is important to get used to the style of asking questions in problems, which may seem very unusual to an unprepared person at the DT.
Kinetic energy
Since a mechanical system has kinetic energy, which depends on the speeds at which its various points move, it can be of a translational or rotational type. The SI unit Joule (J) is used to measure energy.
Let's look at how to find energy. Kinetic energy formula:
- Ex= mv²/2, Ek is kinetic energy measured in Joules;
- m – body weight (kilograms);
- v – speed (meter/second).
To determine how to find the kinetic energy for a rigid body, derive the sum of the kinetic energy of translational and rotational motion.
The kinetic energy of a body moving at a certain speed, calculated in this way, demonstrates the work that must be done by a force acting on the body at rest in order to give it speed.
Potential energy of position at high altitude
Formula (1) is correct provided that the acceleration of gravity g is constant over the entire height of the rise, i.e. in case of rising to a relatively low height. In the gravitational field of any celestial body, the force of gravity and, accordingly, the acceleration of free fall of the body decreases in proportion to the square of the distance from the center of this body. Therefore, when ascending to a high altitude, it should be taken into account that g = g(h) and, therefore, G = G(h):
Here: W is the work against the gravitational force (Joule), G is the gravitational force with which two bodies are attracted to each other (Newton), ma is the mass of the first body (kg), mb is the mass of the second body (kg), r is the distance between the centers of mass of bodies (meter), r1 is the initial distance between the centers of mass of bodies (meter), r2 is the final distance between the centers of mass of bodies (meter), γ is the gravitational constant 6.67 10 -11 (m 3 /(kg sec 2 )),
Potential energy
To find out how to find potential energy, you should apply the formula:
- Ep = mgh, Ep is potential energy measured in Joules;
- g is the acceleration of gravity (square meters);
- m – body weight (kilograms);
- h is the height of the body’s center of mass above an arbitrary level (meters).
Since potential energy is characterized by the mutual influence of two or more bodies on each other, as well as a body and any field, any physical system strives to find a position in which the potential energy will be the least, and ideally zero. potential energy. It should be remembered that kinetic energy is characterized by speed, and potential energy is characterized by the relative position of bodies.
Now you know everything about how to find energy and its value using physics formulas.
Source: elhow.ru