Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными
, а само поле называется
потенциальным
.
Разность потенциалов. Напряжение
Работа сил электростатического поля по перемещению заряда q
0 из точки
1
в точку
2
поля
\(~A_{12} = W_{1} — W_{2} .\)
Выразим потенциальную энергию через потенциалы поля в соответствующих точках:
\(~W_{1} = q_0 \cdot \varphi_1 , W_{2} = q_0 \cdot \varphi_2 .\)
Тогда
\(~A_{12} = q_0 \cdot (\varphi_1 — \varphi_2) .\)
Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.
Из этой формулы разность потенциалов
\(~\varphi_1 — \varphi_2 = \dfrac{A_{12}}{q_0} .\)
- Разность потенциалов
— это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.
В СИ единицей разности потенциалов является вольт (В).
- 1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.
Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ1 — φ2 часто называют электрическим напряжением
между данными точками поля и обозначают
U
:
\(~U = \varphi_1 — \varphi_2 .\)
- Напряжение
между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую.
Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах
.
- 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е
= 1,6·10-19 Кл) между двумя точками, напряжение между которыми равно 1 В.
1 эВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж. 1 МэВ = 106 эВ = 1,6·10-13 Дж.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом
данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
1.4. Работа в электрическом поле. Потенциал
При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна (рис. 1.4.1):
| Рисунок 1.4.1. Работа электрических сил при малом перемещении заряда q |
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение Работа ΔA кулоновских сил на этом перемещении равна
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить
| Рисунок 1.4.2. Работа кулоновских сил при перемещении заряда q зависит только от расстояний r1 и r2 начальной и конечной точек траектории |
Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ кулоновских полей точечных зарядов: Так как каждый член суммы не зависит от формы траектории, то и полная работа A результирующего поля не зависит от пути и определяется только положением начальной и конечной точек.
Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.
Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):
| Wp1 = A10. |
(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
| A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2. |
Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля.
Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
| A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2). |
В Международной системе единиц (СИ) единицей потенциала является вольт (В).
| 1 В = 1 Дж / 1 Кл. |
Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.
Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
| Рисунок 1.4.3. Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда |
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать:
| ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ, |
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует
Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:
| φ = φ1 + φ2 + φ3 + … |
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
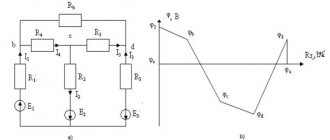
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Разность потенциалов и напряженность
Рассчитаем работу, совершаемую силами электростатического поля при перемещении электрического заряда q
0 из точки с потенциалом φ1 в точку с потенциалом φ2 однородного электрического поля.
С одной стороны работа сил поля \(~A = q_0 \cdot (\varphi_1 — \varphi_2)\).
С другой стороны работа по перемещению заряда q
0 в однородном электростатическом поле \(~A = q_0 \cdot E \cdot \Delta x\).
Приравнивая два выражения для работы, получим:
\(~q_0 \cdot (\varphi_1 — \varphi_2) = q_0 \cdot E \cdot \Delta x, \;\; E = \dfrac{\varphi_1 — \varphi_2}{\Delta x},\)
где Δx
— проекция перемещения на силовую линию.
Эта формула выражает связь между напряженностью и разностью потенциалов однородного электростатического поля. На основании этой формулы можно установить единицу напряженности в СИ: вольт на метр (В/м).
Потенциальная энергия взаимодействия точечных зарядов
Подобно тому, как любое тело, которое взаимодействует с Землей по закону всемирного тяготения, на разных расстояниях от ее центра имеет различную потенциальную энергию, электрический заряд q на разном расстоянии от другого заряда q0 имеет различную потенциальную энергию — W. Если заряд q перемещается в электрическом поле из точки 1, где его потенциальная энергия была W1, в точку 2, где его энергия стала W2 , работа сил поля A = W1 — W2 = -(W2 — W1) = -ΔW. Как видно из формулы, A и ΔW имеют противоположные знаки. Это объясняется тем, что если заряд q перемещается под действием сил поля (т.е. работа поля А положительная), то его потенциальная энергия уменьшается, прирост энергии ΔW — отрицательный. Если же заряд перемещается против сил поля (А — отрицательная), то потенциальная энергия заряда увеличивается. (Такое же соотношение между потенциальной энергией и работой силы тяжести.)
Поскольку буквой Е сказывается напряженность электрического поля, то энергию в электродинамике принято обозначать буквой W.
Как известно, значение потенциальной энергии зависит от выбора нулевого уровня. В электростатике условились потенциальную энергию заряда, размещенного в точке, бесконечно удаленной от заряженного тела, создает поле, считать нулем, W∞ = 0. Тогда, в случае перемещения заряда q с точки 1 в бесконечность, работа поля A = W1 — W∞ = W1 . То есть потенциальная энергия заряда q, размещенного в какой-либо точке поля, численно равна работе, которую выполняют силы поля, перемещая этот заряд с указанной точки в бесконечность: W = qEd, где d — расстояние от источника поля до точки, в которой находится заряд q.
В электротехнике, в отличие от электростатики, под нулем часто принимают потенциальную энергию заряда, размещенного на Земле.
Если поле создано положительным зарядом, то значение потенциальной энергии другого положительного заряда, размещенного в некоторой точке этого поля, будет положительным, если же поле создано отрицательным зарядом, то значение потенциальной энергии положительного заряда — отрицательно. Для отрицательного заряда, размещенного в электрическом поле, все будет наоборот. Когда поле создано сразу несколькими зарядами, потенциальная энергия заряда q, размещенного в какой-либо точке такого поля, равна алгебраической сумме энергий, обусловленных полем каждого заряда в этой точке.