Все о законе Ома: простыми словами с примерами для “чайников”

Первоначальная и современная формулировка

Этот, на первый взгляд, простой закон был сформулирован немецким физиком Георгом Омом в 1826 году. Соответствующую научную статью он опубликовал в следующем году.

Интересно отметить, что появление этой работы не вызвало ажиотажа. Научная общественность оценила открытие Ома лишь после публикации работ физика Пулье аналогичного содержания в 1830 году. В 1833 Ом получил степень доктора в Нюрнбергском университете. В 1872 году единица измерения сопротивления стала называться Омом. В самой простой форме закон для участка цепи звучит так:

Закон носит эмпирический характер, так как он выражает обобщенный анализ большого количества опытных данных.

Сейчас формула закона Ома для полной электрической цепи имеет следующий вид:

I = ℰ / (R+r).

Здесь:

• ℰ — ЭДС источника напряжения, В;
• I — сила тока в цепи, А.
• R — общее сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

Закон Ома для полной цепи учитывает полное сопротивление, которое представляет собой сумму сопротивления цепи R и внутреннего сопротивления источника тока r.

Георг Ом первоначально сформулировал его по-другому. Закон Ома для замкнутой цепи выглядел так:

X = a / ( b + l ), где

• a — величина, характеризующая источник тока. Сейчас говорят, что это электродвижущая сила источника тока;
• b представляет собой свойство электрической установки, которое теперь рассматривается в качестве внутреннего сопротивления источника тока;
• l — величина, зависящая от длины используемых проводов (в современных терминах она соответствует сопротивлению электрической цепи).

Как видно, закон Ома, применяемый для полной электрической цепи, в обоих вариантах имеет одинаковую формулировку.

Также применяется закон Ома в дифференциальной форме. В данном случае рассматриваются очень малые величины. Но это позволяет применять интегральное и дифференциальное исчисление для сложных случаев.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1= I2 ;
• U = U1+ U2 ;
• R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1+ I2 … ;
• U = U1= U2 … ;
• 1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Практическое применение

В большинстве случаев внутреннее сопротивление источника тока считают относительно малым по сравнению с тем, которое есть в электрической цепи. В этом случае применяется закон Ома для замкнутой цепи в сокращенной формулировке: I = U / R.

Чтобы лучше понять, какие физические процессы происходят в электрической цепи, нужно учитывать следующее:

• В источнике тока наблюдаются процессы, которые приводят к тому, что на клеммах образуется разность потенциалов. При подключении к ним электрической цепи по ней идёт ток. Принято считать, что он проходит от положительного потенциала к отрицательному.
• Ток представляет собой упорядоченное движение электронов. В веществе находится огромное количество этих частиц, которые перемещаются с большой скоростью от отрицательного потенциала к положительному.
• Скорость движения электронов зависит от материала проводника, через который они проходят, от его сечения и длины. Если последняя в 2 раза будет увеличена, то это удвоит сопротивление.

В электрической цепи используются резисторы в тех случаях, когда для работы прибора требуется строго определённое сопротивление. Если клеммы источника тока, говоря простыми словами, соединить напрямую, то сопротивление будет малым, а ток относительно большим. С одной стороны, большой ток в некоторых случаях способен расплавить провод, с другой он приводит к ускоренной разрядке батареи.

В веществе движение электронов не является свободным. Перемещаясь, частицы должны преодолевать сопротивление, расходуя на это свою энергию. Величина сопротивления зависит от конкретного материала. В проводниках электроны двигаются относительно легко. Через изоляторы ток пройти не может, за исключением тех случаев, когда подаётся настолько высокое напряжение, что такая ситуация создает пробой.

В полупроводниках происходят более сложные процессы, поскольку они отличаются жесткой кристаллической структурой. При наличии примесей определённого типа может возникать электронная или дырочная проводимость. Ток может представлять собой движение, как электронов, так и дырок.

Более точную характеристику сопротивления можно получить из следующей формулы:

С помощью удельного сопротивления можно охарактеризовать электрические свойства определённого вещества. Эта величина представляет собой сопротивление, которое имеет отрезок провода из данного материала длиной 1 м и площадью сечения 1 кв. мм.

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.

Сопротивление источника тока

Закон Ома для полной электрической цепи и формулы для расчета ее параметров характеризируют не только ток, проходящий через цепь, но и тот, который существует внутри источника тока. Закон Ома для участка цепи не учитывает наличие этой величины.

Батарея аккумулятора обеспечивает перемещение электронов от положительной клеммы к отрицательной. Через электрическую цепь они постоянно движутся в противоположном направлении. Уменьшение их количества на отрицательной клемме и избыток на положительной постоянно компенсируются процессами, происходящими внутри устройства.

Такое движение электронов также является электрическим током. При этом частицам приходится преодолевать внутреннее сопротивление источника тока. При увеличении температуры сопротивление может меняться, характер изменения зависит от конкретного материала.

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Эмпирический характер закона Ома

При изучении природы электричества путем научных исследований происходит формулировка тех или иных законов. Они отличаются межу собой не только своим содержанием, но и тем, как были выведены. Некоторые законы представляют собой следствие из более общих утверждений, другие являются удачной попыткой объяснить многократно наблюдаемые факты.

Закон Ома для однородного участка фактически является попыткой создать правило, которое соответствует большому количеству наблюдений и экспериментов. Его формулировка на протяжении веков подтверждалась на практике, приобретая силу фундаментального закона физики. Закон Ома, представленный в интегральной форме, даёт возможность производить расчёты для различных электрических цепей.

Преобразованные формулы Закона Ома и Джоуля-Ленца

Встретил в Интернете картинку в виде круглой таблички, в которой удачно размещены формулы Закона Ома и Джоуля-Ленца и варианты математического преобразования формул. Табличка представляет собой не связанные между собой четыре сектора и очень удобна для практического применения

По таблице легко выбрать формулу для расчета требуемого параметра электрической цепи по двум другим известным. Например, нужно определить ток потребления изделием по известной мощности и напряжению питающей сети. По таблице в секторе тока видим, что для расчета подойдет формула I=P/U.

А если понадобится определить напряжение питающей сети U по величине потребляемой мощности P и величине тока I, то можно воспользоваться формулой левого нижнего сектора, подойдет формула U=P/I.

Подставляемые в формулы величины должны быть выражены в амперах, вольтах, ваттах или Омах.

Использование для переменного тока

Как известно, в цепи переменного тока действует как активное, так и реактивное сопротивление. Первое из них совпадает с тем, как понимали эту величину во времена Георга Ома. Однако индуктивное и емкостное сопротивления также тормозят движение электронов. В этом случае применяется закон Ома для переменного тока.

Чтобы использовать данный закон в таких цепях, вместо омического сопротивления следует рассматривать полное, которое учитывает суммарное воздействие активной и реактивной составляющих сопротивления.

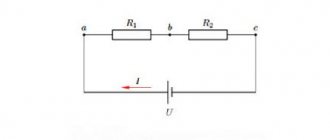
В представленной схеме полное сопротивление обозначается как Z. Омическое, индуктивное и емкостное — соответственно R, XL и XC. Закон Ома для цепи переменного тока учитывает все эти разновидности. Формула расчёта подразумевает, что сложение сопротивлений происходит по правилу векторов.

Для определения всех сопротивлений используют прямоугольный треугольник, один катет которого выражает активное сопротивление, а второй – реактивное. Последнее равно разнице индуктивного и емкостного сопротивлений. Определение полного осуществляется по теореме Пифагора, согласно которой длина гипотенузы равна корню квадратному от суммы квадратов катетов.

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Какая величина тока (I) в этой цепи?

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Какое сопротивление (R) оказывает лампа?

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Какое напряжение обеспечивает батарея?

Применение на практике

Когда нужно работать с электрической цепью, важно знать напряжение, силу тока, сопротивление во всей цепи или на отдельных участках. Если известны две из этих величин, то с помощью закона Георга Ома можно узнать третью без проведения непосредственных измерений.

Иногда требуется использовать закон Ома для неоднородного участка цепи. В этом случае его разбивают на отдельные зоны и сначала проводят вычисления для них.

Поскольку от электрических параметров зависят тепловые или химические воздействия, применяя закон Ома можно рассчитать возможный эффект. В частности, знание таких особенностей позволяет избежать разрушительного эффекта слишком высокой силы тока.

Закон Ома может быть выражен в интегральной и дифференциальной формах. В первом случае речь идёт о традиционной формулировке, а его выражение в дифференциальной форме учитывает удельную проводимость – величину, обратную удельному сопротивлению.

В заключение следует сказать, что измерение сопротивления осуществляется с помощью специального прибора — омметра. Но в работающей цепи это сделать невозможно. Определить величину сопротивления без отключения цепи можно расчетным путем используя закон Ома и предварительно измерив напряжение и силу тока на нужном участке цепи.

Как звучит закон Ома для участка цепи

Есть говорить об официальной формулировке, то закон Ома можно озвучить так:

Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.

Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.

Формула закона Ома

• Чем больше напряжение, тем больше ток.
• Чем больше сопротивление, тем ток меньше.

Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.

Где и когда можно применять закон Ома

Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).

Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.

Ёмкостное сопротивление

Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.

Рисунок 2.

Мы можем использовать следующие соотношения:

Если $I(t)$ определена уравнением (1), то заряд выражен как:

где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:

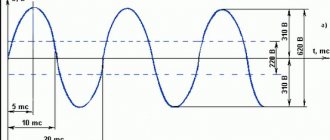
Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac{pi }{2}.$ Амплитуда напряжения на емкости равна:

Величину $X_C=frac{1}{omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $. Это значит, что постоянный ток не течет через конденсатор. Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.

Требуется консультация по учебной работе?Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Интересно почитать: инструкция как прозвонить транзистор.

Индуктивное сопротивление

Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.

Рисунок 3.

Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:

По условию $R=0. mathcal E$ самоиндукции можно выразить как:

Из выражений (8), (9) следует, что:

Амплитуда напряжения в данном случае равна:

где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).