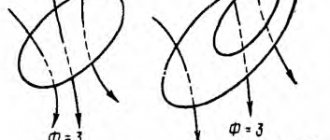Есть двигатель постоянного тока. Задача — разработать, собрать и протестировать устройство, позволяющиее реализовать контур тока применительно к этому двигателю. Желаемое время переходного процесса на застопоренном двигателе (без противо-ЭДС) — не более 10мс. Интерфес связи с внешним управляющим контроллером — SPI. Двигатель постоянного тока, коллекторный, максимальное напряжение 24В, рабочий ток до 5А.
Что значит — контур тока? Самые распространённые драйверы для управления двигателями это всякие вариации полумостов, которые усиливают напряжение. А мне хочется, чтобы драйвер брал на вход не напряжение, а силу тока. Сила, развиваемая электроприводом, прямо пропорциональна силе протекающего тока. А значит, и прямо пропорциональна ускорению на валу двигателя. Такой контур тока позволит избежать извращений, на которые нужно идти без него, как я это делал тут.
Я разбил этот текст на две статьи:
- 1. Измерение сопротивления и индуктивности двигателя
- 2. Разработка управляющего контура
Вот так выглядит макет управляющего железа:
В состав системы будут входить:
- Силовая микросхема ключей, принимающая входной PWM сигнал и усиливающая его.
- Датчик тока.
- Управляющий микроконтроллер, реализующий обратную связь и закон управления.
Датчик тока и его проверка
В качестве датчка тока выбран датчик Холла Allegro ACS714 ($3), выдающий аналоговый сигнал с центром в 2.5В и 185мВ/А, типичная ошибка 1.5%. На датчик была добавлена RC-цепочка в качестве фильтра низких частот с частотой среза 16кГц.
Датчик тока был запитан от 4.96В источника, последовательно с датчиком был подключен резистор, через который было пропущено 2А. Теоретическое напряжение на выходном пине должно быть 4.96/2 + (2 * 0.185 +- 1.5%), измерение показало 2.84 В, что укладывается в расчётные параметры. Затем было поменяно направление течения тока через резистор, при -2А измеренное напряжение на выходном пине датчика составило 2.11В, что опять укладывается в расчётные параметры:
Эта проверка была необходима, т.к. я купил несколько макеток с ACS712 и ACS714 от разных производителей, и в параметры даташита попал только один!
Специфика и особенности трехфазных сетей
Трехфазные электрические сети наиболее эффективно передают ток через промежуточные звенья, вплоть до потребителя. В процессе доставки потери энергии минимальны.
Наличие трехфазной сети в квартире или частном доме очень легко определить. Для этого нужно просто заглянуть в щиток и посчитать количество проводов. Если в наличии 2 или 3 проводника, значит сеть однофазная. В ней два провода являются фазой и нулем. При наличии заземления может быть третий провод. В трехфазных сетях проводов больше на два из-за двух дополнительных фаз. При отсутствии заземления – их всего четыре, а при наличии заземляющего контура – пять.
Эту же задачу можно решить и с помощью вводного автоматического выключателя. К нему также подводится определенное количество проводов, подключаемых в соответствующие клеммы.
В процессе эксплуатации трехфазной сети велика вероятность неравномерного распределения нагрузки по отдельным фазам. Если к одной из них будет подключено только мощное оборудование, а к другим – обычные бытовые приборы, в этом случае может возникнуть ситуация, называемая перекосом фаз. В результате асимметрии тока и напряжения, отдельные потребители могут выйти из строя. Во избежание негативных последствий, нагрузка должна быть равномерно спланирована еще на стадии проектирования и выполнен расчет мощности трехфазной сети.
Трехфазная сеть, по сравнению с однофазной, отличается большим количеством кабельно-проводниковой продукции, автоматов и других устройств. К ней подключается специфическое трёхфазное оборудование Суммарная мощность будет выше ровно в три раза. Значение мощности рассчитывается по току и напряжению с использованием формул.
Микроконтроллер
В качестве управляющего микроконтроллера выбран ATMega328p, работающий на частоте 16МГц. Обвязка микроконтроллера — китайский клон Arduino Nano v3 ($1.5).
Микроконтроллер генерирует ШИМ сигнал через восьмибитный счётчик с делителем 8, таким образом, частота ШИМ сигнала 16 * 10^6 /255 /8 = 7.8 кГц, что укладывается в максимально доступные для драйвера 20кГц.
Делитель АЦП микроконтроллера установлен на 128; поскольку каждое измерение требует примерно 13 тактов, максимальная частота измерений протекающего тока равна примерно 16 * 10^6 / 128 / 13 = 9.6 кГц. Измерения производятся в фоновом режиме, извещая основную программу об окончании при помощи вызова соответствующего прерывания.
Логи
Я долго бился над тем, как записывать происходящее внтри микроконтроллера, ведь памяти у него совсем немного. В итоге я обнаружил, что родной SPI интерфейс очень быстрый, и в итоге вся отладочная информация передаётся микроконтроллером по интерфейсу SPI, для её записи был применён широкодоступный ($10 на дилэкстриме, $6 на алиэкспрессе) китайский клон логического анализатора Saelae Pro 8 Logic. После совсем нетрудных манипуляций по перепрошивке VID/PID, он может быть использован с родным софтом от Saelae. Я пользуюсь sigrok (pulseview). У него исключительно простой формат лог-файлов, которые я просто читаю своей самописной программкой в пятьдесят строк. Я купил этот анализатор по совету gbg, который мне дистанционно чинил мой спектрум (спасибо тебе огромное!), и считаю это самым выгодным вложением денег за последние два года.
Например, я подал синусоидальный сигнал (в ШИМ) на выход контроллера, и логический анализатор его прекрасно видит:
Всё это было соединено вместе, фотография дана в заголовке поста.
Практически все статьи, что я размещаю здесь, являются моим рабочим дневником. Я чему-то учусь (в данном случае теории управления) и старательно записываю то, что узнал. Лучший способ записать — это написать объяснение того, как это всё работает. Затем статьи выкладываю на разных площадках, например тут.
Целей при написании текста у меня две:
а) получить обратную связь от людей, которые знают больше меня.
Например, практически всё, что я узнал для данных двух статей, мне рассказал уважаемый Arastas, прошу любить и жаловать: человек, который тратит личное время на обучение таких оболтусов, как я.
Опять же, gbg, который написал мне линейную алгебру для моих лекций по компьютерной графике, а потом за много тысяч километров по телефону дебажил мне электронику.
б) просто записать:
таким образом я получаю библиотеку личного опыта, к которой периодически возвращаюсь.
Кстати, тематические медиа, какой процент авторов соглашаются на ваши условия программы поддержки?
Преобразование Фурье
Первое, что нужно понять, читая мои тексты: я считаю, что функция и вектор — это одно и то же. Все разговоры про бесконечности на меня навевают скуку и заслоняют суть происходящего. Обобщённые функции и тому подобное — это способ рассмотреть патологические случаи используя тот же самый язык, что и случаи, где никаких патологий нет. Вот только патологии меня не интересуют.
На эту тему хорошо высказался Валерий Иванович Опойцев (Босс):
В любой области полезно оказаться в подходящей среде устного общения, где осыпается книжная шелуха. Там иногда ничего не меняется по сути, зато возникает чувство попадания в колею и освобождения от догм. Для науки, которая всегда в маске, это особенно важно. Суть за кадром, перед глазами — кружева. И вечно чего-то не хватает. То простоты, то сложности, да точно и не определишь — чего. Что-то куда-то шагает, ты — на обочине, а время уходит в песок, не говоря о жизни.
Далее предпринимается попытка сдвинуть ситуацию с места, моделируя письменную среду, где «спадают покровы». Внешняя канва содержания более-менее неясна из оглавления, но главная цель — та, что за кадром. Снять вуаль, грим, убрать декорации. Переупростить, даже приврать слегка, ибо дозирование правды — краеугольный камень объяснения. Результаты, перегруженные деталями, не пролезают куда надо. Озарение случается, когда пухнущая голова проваливается на уровень «дважды два», в то время как счет идет на миллионы. Такая уж тут диалектика.
Если у нас есть вектор (7,12,18,-2), то его можно рассматривать как набор коэффициентов во взвешенной сумме. 7*(1,0,0,0) + 12*(0,1,0,0) + 18*(0,0,1,0) + (-2)*(0,0,0,1). Ровно так же можно считать этот вектор значениями функции в точках 0, 1, 2, 3, ведь наши векторы (0,1,0,0) и ему подобные можно рассматривать как сдвиг единичного импульса: Если постоянно увеличивать количество векторов (сдвинутых единичных импуьсов) в базисе, то получим обычные функции.
К сожалению, с таким базисом бывает довольно неудобно работать. Давайте рассмотрим следующую функцию в качестве примера:
Мы уже беседовали о том, что такое преобразование Фурье. Если кратко, то это смена базиса.
В нашем случае преобразование Фурье — это функция из вещественных чисел в комплексные:
Аргумент функции (вещественное число) — это просто номер базисной функции или вектора (на самом деле, пары базисных функций), а её значение — это соответствующая (пара) координат в для этих двух векторов в базисе. Базис Фурье — это синусы и косинусы различных частот. Частота и является номером базисной функции.
Для нашей конкретной функции f(t), которая уже являетя взвешенной суммой синуса и косинуса, очень легко посчитать её разложение в базис Фурье:
То есть, наша функция f(t) имеет нулевые координаты для всех векторов базиса, кроме векторов номер 11 и 41.
Чем полезен базис Фурье? Например тем, что операция дифференцирования линейно преобразует этот базис. Допустим, мы хотим посчитать преобразование Фурье от производной f'(t). Как это сделать? Как вариант, в лоб: сначала посчитать производную, а затем посчитать преобразование Фурье:
Очевидно, что при дифференцировании sin(x) он станет sin(x+90°), то есть крайне легко найти соответствие разложение в базис Фурье исходной функции и её производной: Умножение на
i
— это просто поворот комплексной плоскости, который соответствует +90° в аргументе нашей функции. То есть, операция дифференцирования, которую сложно делать в базисе единичных импульсов, в базисе Фурье — это просто масштабирование и поворот на 90 градусов. Красиво, правда?
Преобразование Лапласа
Примерно та же самая история происходит и с преобразованием Лапласа. К сожалению, в отличие от базиса Фурье, базис Лапласа неортогонален, поэтому для интуитивного понимания чуточку более сложен. Ну да не суть. Лаплас пошёл немного дальше. Если у Фурье в базисе были только синусоиды, то у Лапласа в базисе синусоиды с экспоненциальным затуханием. Откуда он их взял? Это крайне, крайне полезно при решении линейных дифференциальных уравнений. Давайте подумаем, какая функция преобразуется сама в себя при дифференцировании? Экспонента. А при дифференцировании два раза? Синус. А их комбинации дают все возможные функции, которые могут появиться при решении (линейных) диффуров, что и использовал маркиз дё Лаплас.
Не будем вдаваться в подробности того, как выводятся эти свойства (лучше рассмотрите внимательно свойства базиса Фурье, он проще), давайте просто отметим следующие факты:
1. Преобразование Лапласа линейно:
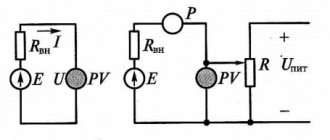
2. Преобразование Лапласа производной — это аффинное действие над преобразованием самой функции: 3. Итак, если у нас есть двигатель постоянного тока, то протекающий ток I(t) и напряжение на клеммах U(t) связаны следующим дифференциальным уравнением, где w(t) — это скорость вращения вала двигателя: Здесь L — это индуктивность, а R — сопротивление, которые мы и ищем. Я не буду повторять, откуда вылезает этот диффур, так как уже подробно и на пальцах его расписывал (см. «уравнения Максвелла на пальцах»).
Поскольку наша задача найти L и R, давайте жёстко зафиксируем вал двигателя, таким образом заставив w(t) быть нулевой:
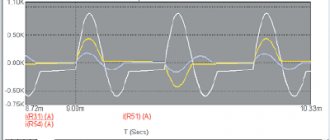
По совету Arastas я подал два типа сигналов на мой двигатель: меандр и синусоиду. Затем я измерил протекающий ток, картинка получается примерно следующая:
Здесь синие кривые — это входное напряжение, котороя я контролирую, а зелёные — это измерения силы тока, полученные при помощи ACS714.
Мой микроконтроллерный код, который генерирует 11 экспериментов с меандром и синусоидами различных амплитуд и частот, можно посмотреть здесь.
Давайте решим наше дифференциальное уравнение для обоих типов сигнала напряжения, получим параметрический выходной сигнал силы тока, и подберём параметры, чтобы теоретическая кривая как можно лучше аппроксимировала реальные измерения.
Пусковые характеристики асинхронных двигателей
Лекция 12. | Пусковые характеристики асинхронныхдвигателей |
| 12.1 | Общие положения |
При подключении асинхронных двигателей к сети в них возникают электромагнитные
и
электромеханические
переходные процессы. В теории электрических машин рассматриваются главным образом
электромеханические
процессы, в которых анализируется только действие установившегося тока. Приведенный ток ротора, при пуске практически равный току статора, и пусковой момент равны:
;
.
Отсюда следует, что ограничение пусковых токов возможно либо увеличением полного сопротивления короткого замыкания, либо уменьшением величины приложенного напряжения. Пусковой момент можно увеличить только до значения максимального момента:
,
которое имеет место в том случае, если:
.
Увеличить пусковой момент можно, либо воздействуя на критическое скольжение, либо уменьшая частоту вращения поля статора. Переходные процессы сопровождаются значительными потерями энергии, которые многократно превышают потери в номинальном режиме работы, и вызывают повышенный нагрев обмоток. Поскольку при пуске: , суммарные электрические потери будут равны:
. (12.1)
Потери в роторе определим через механические параметры:
, (12.2)
где момент определяется из общего уравнения движения привода с учетом момента инерции и момента сопротивления:
. (12.3)
Чтобы выделить потери энергии, обусловленные собственно переходным процессом, предположим, что момент статического сопротивления, приведённый к валу двигателя, равен нулю ,
что имеет место при пуске на холостой ход. Потери энергии в роторе в течение переходного процесса определяются интегрированием потерь мощности по времени и с учётом уравнений (12.2, 12.3) определяются следующим образом:
. (12.4)
Учитывая, что: , получаем:
;
. (12.5)
Из полученного выражения следует, что при пуске без нагрузки потери энергии за время переходного процесса зависят только от суммарного момента инерции системы , синхронной частоты вращения w1
, начального и конечного скольжений.
| 12.2 | Пуск двигателей с фазным ротором |
Пуск двигателей с фазным ротором основан на введении в цепь ротора добавочных активных сопротивлений, обеспечивающих увеличение момента и снижение токов на время пуска. Величина добавочного сопротивления, обеспечивающего получение максимального момента, рассчитывается по формуле:
. (12.6)
Пусковой ток при этом уменьшается и составляет:
. (12.7)
Обычно в процессе пуска добавочные сопротивления регулируют ступенями, обеспечивая определенные пределы изменения тока и момента. При уменьшении момента до значения Мп.min
часть пускового реостата (
r’21доб
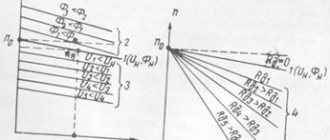
) закорачивается, в результате момент вновь возрастает до максимального значения, и двигатель переходит на новую характеристику. В конечном итоге пусковой реостат полностью выводится, и двигатель выходит на естественную характеристику. Число ступеней определяется требованиями к плавности пуска, а значения сопротивлений находят по пусковой диаграмме (рис. 12.1).
| 12.3. | Двигатели с двойной беличьей клеткой и с глубокопазным ротором |
Двигатели с двойной беличьей клеткой
имеют две короткозамкнутые обмотки ротора, одна из которых является рабочей, а вторая – пусковой. Рабочая обмотка выполняется из медных стержней относительно большого сечения, обладает малым активным сопротивлением, и располагается на значительной глубине от поверхности ротора. Пусковая обмотка выполняется из материалов с повышенным активным сопротивлением (латуни или бронзы), ее стержни имеют относительно малое сечение, и располагаются вблизи поверхности ротора. Между стержнями рабочей и пусковой беличьих клеток имеется узкая щель (рис. 12.2). В результате средняя длина силовых магнитных линий, по которым замыкаются потоки рассеяния рабочей обмотки, значительно меньше, чем для потоков рассеяния пусковой обмотки. Таким образом, пусковая обмотка имеет относительно малое индуктивное сопротивление рассеяния, а рабочая – относительно большое.
Токи в рабочей и пусковой беличьих клетках распределяются обратно пропорционально их полным сопротивлениям:
.
В момент пуска частота тока в роторе велика, индуктивные сопротивления многократно превышают активные, и распределение токов определяется главным образом ими, поэтому на начальной стадии пуска ток в пусковой клетке больше тока в рабочей клетке:
; ; .
Пусковая обмотка имеет повышенное активное сопротивление, и критическое скольжение для нее близко к единице, поэтому она создает большой пусковой момент.
По мере разгона ротора скольжение и частота тока f2
в нем уменьшаются, что приводит к уменьшению индуктивных сопротивлений. В конце пуска они становятся значительно меньше активных сопротивлений, отношением которых и будет в основном определяться распределение токов. При этом ток в рабочей обмотке становится больше тока в пусковой обмотке:
; ; ,
и двигатель будет работать с малым скольжением и высоким к. п.д.
Результирующий момент определяется суммированием моментов, создаваемых пусковой и рабочей обмотками. В области больших скольжений: он существенно увеличивается по сравнению с моментом, создаваемым обычной беличьей клеткой (рис. 12.2 − б).
Двигатели с глубокопазным ротором
имеют в магнитной системе ротора пазы, высота которых в 6 – 12 раз превышает ширину (рис.12.3). Короткозамкнутая обмотка обычно изготавливается путем заливки в эти пазы алюминия или его сплавов. Физические процессы, происходящие в них при пуске, во многом подобны процессам в двигателях с двойной беличьей клеткой. Роль пусковой обмотки при этом играют верхние части сечения стержней, для которых пути замыкания магнитных потоков рассеяния значительно длиннее, чем для нижних частей сечения. В момент пуска частота тока в роторе велика, и распределение токов определяется главным образом индуктивными сопротивлениями. Поскольку индуктивность нижних слоев короткозамкнутой обмотки значительно больше индуктивности ее верхних слоев, поэтому ток вытесняется в верхние слои. В результате эффективная глубина проникновения тока, и эффективное сечение проводников уменьшаются, а активное сопротивление – возрастает. Это приводит к увеличению критического скольжения и пускового момента.
По мере разгона ротора скольжение и частота в нем уменьшаются, что приводит к уменьшению влияния индуктивных сопротивлений на распределение тока по сечению проводников. Эффективная глубина проникновения и эффективное сечение проводников увеличиваются, ток возвращается в нижние слои (рис. 12.3). После окончания разгона плотность тока становится практически одинаковой по всему сечению, активное сопротивление стержней уменьшается, двигатель работает с малым скольжением и высоким к. п.д.
цепи ротора
.
Таким образом, активное сопротивление r’2
в двигателях с глубокопазным ротором изменяется в процессе разгона. Это не влияет на величину максимального момента, но влияет на критическое скольжение, и пусковой момент.
| 12.4. | Пуск асинхронных двигателей путем изменения частоты вращения поля статора |
Ранее было показано, что при прямом пуске в одну ступень потери в роторе независимо от прочих условий равны запасу кинетической энергии инерционной массы , вращающейся с частотой w1: .
Эффективным средством уменьшения потерь является пуск с изменением синхронной частоты вращения. Например, при пуске в две ступени имеем следующие исходные данные:
; ; ; ; .
Подставляя эти значения в исходное уравнение, получим:
.
Электрические потери в роторе на каждом из участков уменьшаются в четыре раза, а суммарные потери – вдвое (рис. 12.4).
При пуске в четыре ступени они сократятся в четыре раза, а при пуске в n
ступеней с равными приращениями: суммарные потери составляют:
(12.8)
и теоретически могут быть сведены к нулю. В действительности это невозможно, поскольку время переходного процесса увеличивается, что приводит к возрастанию потерь холостого хода.
Из уравнений (12.5), (12.8) видно, что при оценке любых переходных процессов важнейшую роль играет постоянная для данного двигателя величина кинетической энергии . Чтобы дать оценку энергетическим свойствам переходных процессов, введём понятие эквивалентного времени разгона, под которым будем понимать время, за которое двигатель, затратив то же количество энергии, что и при реальном пуске вхолостую, разогнался бы из неподвижного состояния до синхронной частоты вращения, если бы разгон шёл с потерями мощности, равным потерям при работе с номинальной нагрузкой:
. (12.9)
Используя это выражение, можно оценить собственные энергетические свойства любого электродвигателя. На рис. 12.5 показано, каким образом эквивалентное время разгона зависит от мощности и числа пар полюсов двигателей серии 4А.
Учитывая полный момент инерции электропривода при переходном процессе, можно найти и эквивалентное время пуска с учётом конкретных условий. Сравнив это время с временем рабочего цикла, можно судить о целесообразности реализации управляемых переходных процессов. Данная задача наиболее актуальна для мощных двигателей с большими инерционными массами.
Уменьшения потерь энергии при пуске асинхронных двигателей достигается за счет реализации следующих мероприятий: снижение суммарного момента инерции, организация пуска без нагрузки; регулирование частоты вращения поля статора.
| 12.5. | Пуск при пониженном напряжении |
Ограничение пусковых токов асинхронных двигателей путем понижения напряжения применяется в том случае, если пуск осуществляется без нагрузки. Ток при этом уменьшается пропорционально напряжению, а момент – пропорционально его квадрату, то есть – в значительно большей степени. Например, при пуске путем переключения обмоток со звезды на треугольник напряжение и ток уменьшаются в раз, а момент – в три раза.
В общем случае пуск обеспечивается в том случае, если выполняется условие:
, (12.10)
где µп
и
Мном
– кратность пускового момента (приводится в каталожных данных) и номинальный момент электродвигателя; – относительное снижение напряжения;
Мс0
– момент статического сопротивления при трогании, приведенный к валу двигателя; – минимально необходимый для обеспечения успешного пуска избыточный момент (обычно принимается равным ).
Из условия (12.10) можно определить минимально необходимое для успешного пуска напряжение:
. (12.11)
Момент статического сопротивления, который существенно влияет на пусковые характеристики, является функцией частоты вращения. Наиболее тяжелые условия пуска имеют место для характеристик постоянного момента: В системе относительных единиц: ; при этом получим:
. (12.12)
Из этого выражения следует, что снижение напряжения при пуске возможно только в том случае, если для кратности пускового момента выполняется условие:
. (12.13)
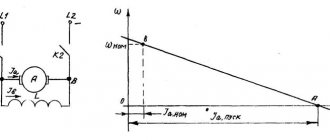
Избыточный момент в процессе пуска под нагрузкой не остается постоянным, и зависит от закона изменения момента сопротивления. Из характеристик, показанных на рис. 12.6 – а, видно, что при вентиляторном моменте сопротивления момент М(U)
, развиваемый двигателем при пониженном напряжении, всегда больше момента сопротивления, поэтому пуск произойдет успешно, и двигатель будет устойчиво работать в точке
А
при небольшом уменьшении установившихся значений частоты вращения и момента. При характеристике постоянного момента (рис. 12.6 – б) снижение напряжения приводит к тому, что на участке
Б – В
момент сопротивления превышает момент, развиваемый двигателем, и разгон двигателя до точки установившейся работы в этих условиях невозможен.
В таких случаях необходимо обеспечивать пуск без нагрузки. Для этого применяются особые методы, которые включают в себя блокировки от завалов в системах автоматического управления, транспортерами, использование упругих звеньев и разгонных муфт при сочленении двигателей и рабочих механизмов, которые обеспечивают сцепление с нагрузкой только после того, как двигатель разгонится.
| 12.6. | Пуск в условиях соизмеримой мощности |
В условиях эксплуатации прямой пуск асинхронных двигателей большой мощности электроснабжения может вызвать значительные просадки напряжения на участке сети. Это может привести не только к нарушению условий успешного пуска (12.10 – 12.12), но и отрицательно влияет на характеристики других потребителей, подключенных в непосредственной электрической близости.
Кратковременные снижения (провалы) напряжения по-разному влияют на работоспособность электроприемников: в определенных пределах они не представляют опасности для вращающихся электрических машин, обладающих достаточным запасом кинетической энергии, но могут вызвать отключение магнитных пускателей, погасание люминесцентных ламп, сбои в работе персональных компьютеров, и нарушение нормального функционирования многих других электроприемников. Провалы напряжения объясняются большим увеличением тока и полной мощности, потребляемой двигателем из сети при пуске. Как было показано ранее, вторичное напряжение трансформаторов зависит не только от величины, но и от характера нагрузки, а его относительное изменение определяется по формуле:
, (2.14)
где – приведенные значения вторичных напряжений в режимах холостого хода и нагрузки; – коэффициент нагрузки, характеризующий модуль тока; активная и реактивная составляющие напряжения короткого замыкания трансформатора, о. е.; – фазовый угол нагрузки.
Для выявления некоторых особенностей изменений напряжения при пуске асинхронных двигателей запишем это выражение в более удобном для анализа виде. Учитывая, что активная и реактивная составляющие напряжения короткого замыкания равны:
и известную формулу тригонометрических преобразований:
,
получаем:
. (2.15)
Оценим с помощью этого выражения относительные потери напряжения при пуске. Коэффициент загрузки в момент пуска увеличивается пропорционально току, фазовый угол j2
при нагрузке, близкой к номинальной, находится в пределах: , а при пуске весьма близок к фазовому углу короткого замыкания трансформатора
jк
: , т. е. . Отсюда несложно получить отношение:
, (2.16)
из которого следует, что при кратности пускового тока kI
= (5 – 7
) относительные потери напряжения, вызываемые пусковыми токами, могут возрастать по сравнению с потерями, имеющими место при номинальном токе, в 7 – 10 раз. При ограниченной мощности трансформатора и участка сети, к которому подключается двигатель, это приводит к значительным снижениям напряжения в этой точке.
Правила устройства электроустановок допускают снижение напряжения на зажимах пускаемого асинхронного двигателя до 30%, на зажимах работающих двигателей – до 20 %. Для расчета фактического снижения напряжения необходимо знать конфигурацию электрической сети и параметры всех ее элементов и нагрузок. На рис. 2.17 приведена типичная для сетей ограниченной мощности расчетная схема.
Относительное значение напряжения U*12
на общих шинах запускаемого электродвигателя и подключенной к ним нагрузки рекомендуется определять по формуле:
, (2.17)
где zтр,
zл
– полные сопротивления трансформатора и линии электропередачи;
zд
– сопротивление короткого замыкания пускаемого электродвигателя;
zн1,zн2
– сопротивления нагрузок.
С целью упрощения расчетов и внесения в их результаты определенного запаса, учитывающего неоднозначность исходных данных, в выражении (2.17) арифметически суммируются модули полных сопротивлений. Если нагрузки заданы токами, их сопротивления определяются по формулам:
. (2.18)
Сопротивление короткого замыкания пускаемого электродвигателя рассчитывается по номинальным значениям напряжения, тока и кратности пускового тока , которые всегда приводятся в каталожных данных:
. (2.19)
Входной сигнал — функция Хэвисайда (полупериод меандра)
Итак, w(t) = 0, начальные условия I(0) = 0, ток в самом начале не течёт. Приложим постоянное напряжение U0 к клеммам мотора, как себя должен будет вести протекающий ток?
Давайте возьмём преобразование Лапласа от левой и правой частей дифференциального уравнения (1):
Для получения второй строчки я использовал линейность преобразования Лапласа, U0/s — взял из таблицы (обычно преобразования Лапласа вручную не считают, пользуются таблицами).
Для получения третьей строки использовано свойство производной.
Последняя строчка получается из предпоследней использованием метода неопределённых декомпозиций. Смысл этого перехода в том, чтобы опять получить табличную функцию. Разумеется, в двадцать первом веке руками это считать ни к чему.
Теперь осталось применить обратное преобразование Лапласа (для правой части мы смотрим таблицу) и мы решили наш диффур. Переход в базис Лапласа превратил дифференциальное уравнение в обычное алгебраическое!
Быстрая проверка результата: по истечении нескольких миллисекунд индуктивность уже не будет играть роли, и мы получим протекающий ток U_0 / R (закон Ома). В самом же начале протекающий ток равен нулю и экспоненциально возрастает, причём скорость возрастания напрямую зависит от индуктивности. Sanity check passed.
Файл с измерениями лежит здесь. Три колонки, секунды, приложенное напряжение (в вольтах), измеренная сила тока (в амперах).
Вот код, который подбирает параметры сопротивления и индуктивности для этого эксперимента:
Скрытый текст
import numpy as np from scipy.optimize import curve_fit import matplotlib.pyplot as plt U0 = 19.2 def unit_step_current(x, R, L): return [U0/R — U0/R*np.exp(-t*R/L) for t in x] data = np.genfromtxt(‘unit_step_19.2V.csv’, delimiter=’,’, names=[‘t’, ‘V’, ‘A’]) [R, L] = curve_fit(unit_step_current, data[‘t’], data[‘A’])[0] print(R, L) fig = plt.figure() ax1 = fig.add_subplot(1,1,1) ax1.set_title(«Resistance/inductance fitting») ax1.set_xlabel(‘Time, seconds’) ax1.set_ylabel(‘Current (A), tension (V)’) ax1.plot(data[‘t’], data[‘V’], color=’b’, label=’input tension’) ax1.plot(data[‘t’], data[‘A’], color=’g’, label=’measured current’) model=unit_step_current(data[‘t’], R, L) ax1.plot(data[‘t’], model, color=’r’, label=’fitted curve’) ax1.legend() plt.show()
Он говорит, что хорошо подходит пара R=4.4 Ома, L=6мГенри, вот график:
Инструмент для замеров.
Измерение каждой величины следует повторить в разных местах, чтобы не впасть в ошибку из-за неправильности одного измерения.
Внутренний диаметр статора или, как часто говорят диаметр его расточки D является одним из самых важных размеров двигателя; так как от размеров сердечника статора и точности его измерения зависит правильность определения других размеров, его нужно производить по возможности тщательнее.
Наилучшим инструментом для этого является внутренний микрометр (микроскопический штихмас); при его помощи можно измерить диаметр расточки в любом месте.
Обычно такие штихмасы изготовляются для измерений от 50 до 63 или 70 мм; к ним придаются комплекты удлиняющих насадок, позволяющих расширять микрометрический штихмас с точностью измерения до нескольких сотых миллиметра. Если этого инструмента нет, то для диаметров до 200 — 250 мм можно пользоваться штангенциркулем; однако это не всегда удается, так как зачастую сердечник статора сидит настолько глубоко в корпусе, что губки штангенциркуля его не захватывают. В таких случаях можно производить измерение посредством обыкновенного штихмаса, изготовленного из куска стальной проволоки; после подгонки такого штихмаса к диаметру расточки длина его измеряется штангенциркулем.
При диаметрах больше 250 — 300 мм можно применять и обыкновенный слесарный кронциркуль с масштабной линейкой, хотя это значительно менее точно.
При измерении внутреннего диаметра нужно следить за тем, чтобы оно производилось между серединами двух противоположных зубцов, так как края зубцов могут могут быть несколько завалены внутрь паза.
Замеряемые значения.
Наружный диаметр статора Dн не всегда удается измерить непосредственно; измерение осуществляется проще всего, если сердечник статора запрессован в корпус без всякого промежутка между ними, как это обычно делается в закрытых двигателях; тогда можно просто измерить диаметр расточки корпуса. Если же сердечник статора сидит в корпусе на лапках, составляющих часть самого сердечника, или не приливах к корпусу, то измерению могут воспрепятствовать нажимные кольца, сжимающие сердечник. Обычно их наружный диаметр примерно равен наружному диаметру статора, но они зачастую сидят на своих местах не вполне точно, с некоторым сдвигом, который препятствует правильному захвату статора губками штангенциркуля. Тогда можно поступить так: вместо измерения диаметра измерить высоту статора вместе с зубцами в направлении радиуса при помощи штангенциркуля, просунув одну из его губок в промежуток между сердечником статора и корпусом, притом так, чтобы сдвинутое нажимное кольцо оказалось в вырезе, которым обычно снабжаются губки штангенциркуля у своего основания. Если обозначить измеренную таким способом толщину статора через hc, то наружный диаметр будет равен:
DH = D + 2hc (см)
Высота тела статора hs при наличии промежутка между сердечником статора и корпусом измеряется так же, как и величина hc при наличии промежутка между сердечниками статора и корпусом измеряется так же, как и величина hc. Если же промежутка нет, то она получается вычислением из других величин (см. ниже).
Длина сердечника статора в осевом направлении ln является не очень строго определенной величиной; поэтому ее измерение можно производить как измерение осевой длины статора штангенциркулем, так и простой масштабной линейкой. Однако ее никогда не следует измерять по головкам зубцов, потому что зубцы по концам всегда несколько расходятся в стороны, образуя так называемый «веер». Правильное значение получается при измерении этой величины по дну паза.
Общее число пазов статора Z определяется счетом; оно всегда делится на 3 и обычно четное.
Размеры пазов и зубцов статора, подлежащие измерению, зависят от их формы. Различаются пазы:
- открытые; с шириной отверстия равной ширине паза;
- полузакрытые, имеющие отверстие шириной, меньшей ширины паза;
- закрытые, вовсе не имеющие отверстия.
Открытые пазы, характерные для современных более или менее крупных машин, имеют всегда прямоугольную форму и снабжены у отверстия заплечиками для установки клина; измерению в них подлежат: ширина, полная глубина и глубина ниже заплечиков.
Полузакрытые пазы значительно разнообразнее по форме, которые следует измерять. Здесь можно дать только некоторые общие указаний к этой наиболее кропотливой части обмера.
- Способ оттиска; берутся две пластинки из листового свинца толщиной 2 — 3 мм такой величины, чтобы каждая из них могла прикрыть два-три паза. Для получения оттиска эти пластинки кладутся на торец сердечника по концам какого-либо его диаметра и прикрываются массивной полосой с отверстием в середине. Другая подобная же полоса располагается с противоположной стороны сердечника; через отверстия в обеих полосах пропускается болт Затягиванием гайки свинец вжимается в пазы и получает их оттиск, который затем тщательно обмеривается при помощи штангенциркуля с острыми губками или чертежного циркуля-измерителя и десятичного масштаба. Вместо свинца может быть применен мягкий, но не слоистый картон. Получение оттиска путем удара молотком по свинцовой пластинке через прокладку не рекомендуется, так как оттиск при этом сбивается и получается неточным.
- Способ клинообразного щупа: две стальные масштабные линейки длиной по 150 мм и шириной 20 мм срезаются наискось так. Клинообразные щупы; получаются два клинообразных щупа, один из которых служит для измерения от 1 до 15 мм, а другой от 10 до 20 мм.
Входной сигнал — синус
Повторим процедуру для синусоиды напряжения с амплитудой U0 и частотой F0. Применим преобразование Лапласа к уравнению (1), сначала к правой части: а потом и к левой: Теперь обратное преобразование нам даст следующий закон протекания тока: Опять быстрый sanity check: нулевой ток в самом начале, несколько миллисекунд переходных процессов (экспонента, напрямую зависящая от индуктивности). По истечению некоторого времени протекающий ток — это взвешенная сумма синуса и косинуса одной и той же частоты (частота равна входной, это хорошо). Эта сумма даёт синусоиду, чуть сдвинутую во времени. Отлично, результат правдоподобен.
Измерения лежат здесь, а код подбора параметров тут. Он даёт примерно такие же значения сопротивления и индуктивности, что нам и требовалось. Вот график:
Почему не измерить параметры напрямую, зачем весь этот огород с микроконтроллерами? Во-первых, мне нечем измерять индуктивность. Да и измерение сопротивления двигателя омметром может иметь свои нюансы.
Далее, параметры, найденные при высокой амплитуде сигнала, не совсем совпадают с тем, что получается при низких напряжениях. Может быть интересно (тут не рассмотрено) делать модель не только двигателя, а всей системы в целом, включая нелинейность ШИМ-драйвера.
Ну а дальше осталось разработать регулятор, который будет на вход брать необходимую силу тока. Оставайтесь на связи!
Как рассчитать мощность электродвигателя
Как выполнить расчёт потребляемой мощности асинхронного электродвигателя из сети, если по шильдикам можно узнать только номинальную мощность? Для этого необходимо:
- обратить внимание на остальные показатели – это η и cosφ (КПД и коэффициент мощности);
- учесть связь динамических характеристик вала и КПД.
По имеющимся данным, можно рассчитать затраченную мощность электроэнергии:
Pз=Р/η.
Но нужно помнить, что потребляемая энергия электрическими приборами включает в себя как активную, так и реактивную компоненту.