| Угловая частота | |
| ω | |
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы | градус/с |
Углова́я частота́
(синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
ω = ∂ φ / ∂ t .
Другое распространённое обозначение ω = φ ˙ . >.>
Угловая частота связана с частотой ν соотношением [1]
ω = 2 π ν . u >.>
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
ω = 360 ∘ ν . u >.>
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2 π единиц времени.
Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC
-контура равна ω L C = 1 / L C , =1/>,> тогда как обычная резонансная частота ν L C = 1 / ( 2 π L C ) . u _=1/(2pi >).>
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2 π и 1/(2 π ), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
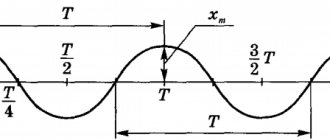
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:
.
В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:
.
Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Частные случаи формул для вычисления циклической частоты
Груз на пружине (пружинный маятник — идеальная модель) совершает гармонические колебания с круговой частотой равной:
\[{\omega }_0=\sqrt{\frac{k}{m}}\left(7\right),\]
$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:
\[{\omega }_0=\sqrt{\frac{mga}{J}}\left(8\right),\]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Примером физического маятника является математический маятник. Круговая частота его колебаний равна:
\[{\omega }_0=\sqrt{\frac{g}{l}}\left(9\right),\]
где $l$ — длина подвеса.
Угловая частота затухающих колебаний находится как:
\[\omega =\sqrt{{\omega }^2_0-{\delta }^2}\left(10\right),\]
где $\delta $ — коэффициент затухания; в случае с затуханием колебаний ${\omega }_0$ называют собственной угловой частотой колебаний.
Примеры движения
Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.
В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:
- тела, подвешенного на пружине (двигающееся по направлению вверх-вниз);
- груза на нитке;
- электрического контура и других.
Ссылки и примечания [ править ]
- ^ ab
Каммингс, Карен; Холлидей, Дэвид (2007).
Понимание физики
. Нью-Дели: John Wiley & Sons Inc., авторизованная перепечатка для Wiley — Индия. стр. 449, 484, 485, 487. ISBN 978-81-265-0882-2 .(UP1) - Holzner, Стивен (2006). Физика для чайников
. Хобокен, Нью-Джерси: Wiley Publishing Inc., стр.201 . ISBN 978-0-7645-5433-9 . угловая частота. - Лернер, Лоуренс С. (1996-01-01). Физика для ученых и инженеров
. п. 145. ISBN 978-0-86720-479-7 . - Мор, JC; Филлипс, WD (2015). «Безразмерные единицы в СИ». Метрология
.
52
(1): 40–47. arXiv : 1409.2794 . Bibcode : 2015Metro..52 … 40M . DOI : 10.1088 / 0026-1394 / 52/1/40 . S2CID 3328342 . - Перейти
↑ Mills, IM (2016). «В единицах радиан и цикл для угла плоскости величины».
Метрология
.
53
(3): 991–997. Bibcode : 2016Metro..53..991M . DOI : 10.1088 / 0026-1394 / 53/3/991 . - «Единицы СИ необходимо реформировать, чтобы избежать путаницы» . От редакции. Природа
.
548
(7666): 135. 7 августа 2011 г. doi : 10.1038 / 548135b . PMID 28796224 . - PR Бункер; IM Mills; Пер Дженсен (2019). «Постоянная Планка и ее единицы». J Quant Spectrosc Radiat Transfer
.
237
: 106594. дои : 10.1016 / j.jqsrt.2019.106594 . - PR Бункер; Пер Дженсен (2020). «Постоянная Планка действия А ». J Quant Spectrosc Radiat Transfer
.
243
: 106835. дои : 10.1016 / j.jqsrt.2020.106835 . h {\displaystyle h} - Serway, Raymond A .; Джуэтт, Джон В. (2006). Основы физики
(4-е изд.). Белмонт, Калифорния: Brooks / Cole — Thomson Learning. стр. 375, 376, 385, 397. ISBN 978-0-534-46479-0 . - Нахви, Махмуд; Эдминистер, Джозеф (2003). Очерк теории и проблем электрических цепей Шаума
. Компании МакГроу-Хилл (McGraw-Hill Professional). стр. 214, 216. ISBN 0-07-139307-2 .(LC1)
Связанное чтение:
- Оленик, Ричард П .; Апостол, Том М .; Гудштейн, Дэвид Л. (2007). Механическая Вселенная
. Нью-Йорк: Издательство Кембриджского университета. С. 383–385, 391–395. ISBN 978-0-521-71592-8 .
Амплитуда, период и частота
Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.
Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:
- Время, за которое маятник приходит в одно и то же положение, называется периодом колебаний.
- Количество колебаний в единицу времени представляет собой частоту. Она измеряется в Герцах (Гц). Имеет обратную зависимость от периода.
- Циклическая частота колебаний (угловая, круговая) представляет собой количество колебаний за 2 π секунд. Обозначается греческой буквой омега. Она вводится для упрощения расчетов в теоретической физике и электронике. Единица измерения циклической частоты рад/с.
- Если имеется два графика функций с одинаковой частотой, но сдвинуты относительно друг друга, то различна их фаза колебаний.
единицы измерения
Единицей измерения СИ является герц . Первоначально эта единица была введена в 1930 году Международной электротехнической комиссией [ 13 ] , а в 1960 году она была принята для общего пользования XI Генеральной конференцией по мерам и весам в качестве единицы СИ. До этого в качестве единицы измерения частоты использовался один цикл в секунду
(1 цикл в секунду = 1 Гц) и производные как килоцикл в секунду, мегацикл в секунду, километр в секунду, равные килогерцу, мегагерцу и гигагерцу соответственно).
Математический маятник
Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.
Также нить должна быть невесомой и нерастяжимой.
Груз в этом случае считается материальной точкой.
При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:
α=x/l.
На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l
Вторая производная уравнения движения дает a=-(ω)^2x
Таким образом: -gx/l=-(ω)^2x -> ω ^2=g/l.
Период: T=2π /ω T=2π*sqrt (g/l)
Это формула Галилея, которая описывает движение математического маятника.
Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.
Другие значения, связанные с частотой
- Пропускная способность
— ν m a x − ν m i n {\displaystyle \nu _{max}-\nu _{min}} - Частотный диапазон
— l o g ( ν m a x / ν m i n ) {\displaystyle log(\nu _{max}/\nu _{min})} - Отклонение частоты
— Δ ν / 2 {\displaystyle \Delta \nu /2} - Период
— 1 / ν {\displaystyle 1/\nu } - Длина волны
— v / ν {\displaystyle {v}/\nu } - Угловая
скорость (скорость вращения) — d ϕ / d t ; 2 π F B P . {\displaystyle d\phi /dt;2\pi F_{BP.}}
Пружинный маятник
Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.
Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:
F=-kx.
Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.
По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.
После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.
Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.
Угловая скорость
Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.
Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.
Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:
где:
- ω – угловая скорость (рад./с);
- ∆ϕ – изменение угла отклонения при повороте (рад.);
- ∆t – время, затраченное на отклонение (с).
Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.
Угловая скорость в конкретных случаях
На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.
Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.
где:
- π – число, равное 3,14;
- ν – частота вращения, (об./мин.).
В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:
ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.
К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.
Как определить угловую скорость
Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:
Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.
Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.
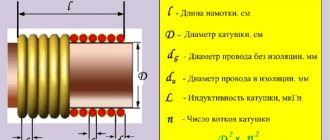
Колебательный контур
Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.
В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.
Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.
Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.
Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.
Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.
Метрологические аспекты
Для измерения частоты применяют различные типы частотомеров , в том числе: для измерения частоты импульсов — счетчики электронов и конденсаторов, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры , а также анализаторы спектра . Для воспроизведения частоты с определенной точностью используются различные меры, такие как стандарты частоты высокой точности, синтезаторы частоты , генераторы и другие. Частоты сравниваются компаратором частот или с помощью осциллографа .по кривым Лиссажу .
Расчет частот
Расчет частоты повторяющегося события осуществляется с учетом количества повторений этого события в течение заданного периода времени. Полученная сумма делится на продолжительность соответствующего временного интервала. Например, если за 15 секунд произошло 71 однородное событие, то частота будет равна:
ν = 71 15 s ≈ 4 , 7 Hz {\displaystyle \nu ={\frac {71}{15\,{\mbox{s}}}}\approx 4{,}7\,{\mbox{Hz}}}
Если количество полученных отсчетов невелико, то более точным методом является измерение временного интервала для заданного числа появлений рассматриваемого события, а не нахождение числа событий в пределах заданного интервала времени. [8]. Использование этого последнего метода вносит случайную ошибку между нулем и первой выборкой, усредняя половину выборки; это может привести к появлению средней ошибки в расчетной частоте Δν = 1/( 2Tm
)
или относительной ошибки Δν /
ν=
1/(
2vTm)
, где
Tm —временной
интервал, а νизмеряемая частота. Ошибка уменьшается с увеличением частоты; поэтому эта проблема более существенна для низких частот, где число отсчетов N невелико.
Методы измерения
Стробоскопический метод
Использование специального прибора, стробоскопа, является одним из исторически старейших методов измерения частоты вращения или вибрации различных объектов. При измерении используется источник стробоскопического света (обычно яркая лампа, периодически дающая короткие вспышки света), частота которого регулируется предварительно калиброванной синхронизирующей схемой. На вращающийся объект направляют источник света, после чего частота вспышек постепенно меняется. Когда частота вспышек равна частоте вращения или вибрации объекта, последний успевает совершить полный цикл колебаний и вернуться в исходное положение в промежутке между двумя вспышками, так что при освещении лампой Строб , этот объект будет казаться неподвижным. Однако у этого метода есть недостаток:Если частота вращения объекта (x) не равна частоте строба (y), а пропорциональна ей с целым коэффициентом (2x, 3x и т. д.), объект все равно будет казаться неподвижным .
Метод стробоскопа также используется для регулировки скорости вращения (вибрации). При этом частота вспышек фиксируется, а частота периодического движения объекта изменяется до тех пор, пока он не начнет казаться неподвижным.
Метод встряхивания
Близким к стробоскопическому методу является метод ударов. Он основан на том, что при смешении колебаний двух частот (опорной ν
и измерительной
ν ‘ 1) в нелинейном контуре разность частот Δν = |
ν
—
ν’ 1 |, называемая частотой биений , при линейном сложении колебаний эта частота является частотой огибающей полного колебания. Метод применим, когда предпочтительнее измерять низкочастотные колебания с частотой Δ
f
. В радиотехнике этот метод известен также как гетеродинный метод измерения частоты. В частности, метод ритма используется для настройки музыкальных инструментов. При этом звуковые колебания фиксированной частоты (например, от камертона), раздающиеся одновременно со звуком настраиваемого инструмента, создают периодическое усиление и затухание общего звука. При точной настройке прибора частота этих времен стремится к нулю.
Применение счетчика частоты
Высокие частоты обычно измеряются частотомером. Это электронное устройство, которое оценивает частоту определенного повторяющегося сигнала и отображает результат на цифровом дисплее или аналоговом датчике. Дискретные логические элементы цифрового частотомера позволяют учитывать количество периодов колебаний сигнала в пределах определенного интервала времени, подсчитываемых эталонными кварцевыми часами . Периодические процессы, которые не являются электрическими по своей природе (например, вращение вала, механическая вибрация или звуковые волны), могут быть преобразованы в периодический электрический сигнал с помощью измерительного преобразователя.и таким образом подаются на вход частотомера. В настоящее время устройства этого типа способны перекрывать диапазон до 100 ГГц; эта цифра представляет собой практический предел для методов прямого подсчета. Самые высокие частоты измеряются косвенными методами.
Косвенные методы измерения
За пределами диапазона, доступного для частотомеров, частоты электромагнитных сигналов часто оцениваются косвенно с использованием гетеродинов (т. Е. Преобразователей частоты). Опорный сигнал известной частоты объединяется в нелинейном смесителе (например, диоде ) с сигналом, который необходимо настроить на частоту; в результате формируется гетеродинный сигнал или как вариант биениягенерируются разностью частот между двумя исходными сигналами. Если последние достаточно близки друг к другу по своим частотным характеристикам, то гетеродинный сигнал достаточно мал, чтобы его можно было измерить одним и тем же частотомером. Следовательно, в результате этого процесса оценивается только разница между неизвестной частотой и опорной частотой, которую необходимо определять другими методами. Можно использовать несколько ступеней микширования для охвата еще более высоких частот. В настоящее время проводятся исследования по распространению этого метода на частоты видимого и инфракрасного света, так называемое гетеродинное оптическое обнаружение.