Зависимость силы тока от напряжения. Сопротивление

3.9

Средняя оценка: 3.9

Всего получено оценок: 98.

3.9

Средняя оценка: 3.9

Всего получено оценок: 98.

Электрический ток — это упорядоченное движение электрических зарядов или заряженных макроскопических тел. Направление электрического тока I совпадает с направлением движения положительно заряженных частиц: заряды движутся под воздействием электрического поля, которое создается в проводнике в результате приложенного к концам проводника напряжения U. Как величина силы тока зависит от величины напряжения? Попробуем разобраться.

Величина силы тока

По определению силой тока называется физическая величина равная величине заряда q, прошедшего через поперечное сечение проводника за время t:

$$ I = { q\over t } $$

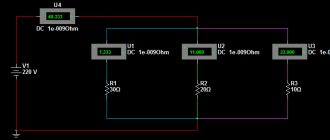
Если сила тока не зависит от времени, то такой электрический ток называется постоянным. Рассмотрим далее именно такой случай, когда ток постоянен. Измерить величину заряда чрезвычайно трудно, поэтому в 1826 г. немецкий физик Георг Ом поступил следующим образом: в электрической цепи, состоящей из источника напряжения (батареи) и сопротивления, он измерял величину тока при разных значениях сопротивления. Затем, не меняя величину сопротивления, он стал изменять параметры источника напряжения, подключая сразу, например, два-три источника. Измеряя величину тока в цепи, он получил зависимости силы тока от напряжения U и от сопротивления R.

Рис. 1. Схема измерений тока и напряжения Георга Ома.

Вольт-амперная характеристика

С её помощью можно узнать, как изменяется ток при увеличении или уменьшении напряжения в цепи. Если её строить для проводника, зависимость будет линейной. Это можно понять из закона Ома, в соответствии с которым сила пропорциональна приложенной разности потенциалов. Такого вида график характерен для металлов. Но в то же время для полупроводников он не будет линейным.

Всё дело в том, что такие материалы обладают особыми свойствами. В них может наступать пробой — явление, при котором происходит резкое возрастание силы тока и процесс насыщения. В последнем случае значение электротока практически не изменяется при росте напряжения.

График зависимости строят в декартовой системе координат. По оси X откладывают напряжение, а Y — ток. Исследовать характеристику для любого элемента цепи можно и самостоятельно. Для этого потребуется подготовить:

• регулируемый блок питания;
• амперметр;
• вольтметр;
• исследуемый элемент.

Схема собирается довольно просто. К блоку питания подключают измеритель тока (амперметр), к выходу которого подсоединяют одним выводом проводник. Второй полюс соединяют со свободным контактом источника напряжения. Измеритель напряжения включают параллельно исследуемому элементу.

Эксперимент заключается в следующем. С помощью блока питания изменяют напряжение, величина которого снимается с вольтметра. Одновременно списывают данные с амперметра. Затем рисуют координатные оси ВАХ, на которых откладывают точки соответствующих величин и соединяют их плавной линией. Нарисованная кривая или прямая и будет отображать реальную картину зависимости тока от напряжения для элемента. По ВАХ можно построить график зависимости мощности от силы тока. Для этого необходимо выполнить расчёт по формуле: P = I*U.

На практике часто приходится иметь дело с переменным током. Это явление, при котором его сила изменяется с течением времени. В этом случае не используют ВАХ, так как изменение U происходит по определённому закону, чаще всего синусоидальному, поэтому, если нужно построить график зависимости напряжения от времени, необходимо знать формулу, с помощью которой описывается функция.

Закон Ома

В результате проведенных исследований Георг Ом обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I в цепи есть величина постоянная:

$$ R= { U \over I } $$

где R — электрическое сопротивление. Данная формула называется законом Ома, который до сих пор является основным расчетным инструментом при проектировании электрических и электронных схем.

Если по оси абсцисс отложить значения напряжения, а по оси ординат — значения тока в цепи при данных значениях напряжения, то получится график зависимости силы тока I от напряжения U.

Из этого графика видно, что эта зависимость линейная. Угол наклона прямой зависит от величины сопротивления. Чем больше R, тем меньше угол наклона.

Если зафиксировать напряжение U и по оси абсцисс откладывать значения R электрического сопротивления, то из полученного графика видно, что эта зависимость уже нелинейная — с ростом сопротивления поведение тока описывает обратно пропорциональной функцией — гиперболой.

Закон Ома перестает работать при больших величинах тока, так как начинают работать дополнительные эффекты, связанные с тепловым разогревом вещества, ростом температуры. В газах при больших токах возникает пробой, ток растет лавинообразно, отклоняясь от линейного закона.

Связь между параметрами

Чтобы появился электрический ток, необходимо выполнение нескольких условий. Нужен его источник, материал, имеющий свободные носители заряда, и замкнутая цепь, по которой они смогут перемещаться. После изобретения «вольтова столба» учёные начали проводить различные эксперименты, изучая протекание электротока. В 1825 году Ом в своих опытах с использованием гальванического источника и крутильных весов наблюдал потерю энергии в зарядах. Он обнаружил, что сила тока в цепи зависит не только от типа материала, но и его линейных характеристик.

Анализируя полученные данные, Ом вывел формулу: X = a*k/L, где: X — сила электротока, a — электрическое напряжение, k — коэффициент проводимости, l — длина материала. Впоследствии этот закон был подтверждён другими учёными и был назван в честь открывателя.

В современном виде он записывается так: I = U/R, где:

• U — разность потенциалов (напряжение);
• R — сопротивление.

То есть сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна его сопротивлению. R — коэффициент пропорциональности. По своему определению он является величиной, обратной проводимости. Зависит сопротивление от физических размеров проводника и его способности препятствовать прохождению электротока.

Вычислить значение R можно по формуле: R = pL/S, где p — удельный коэффициент, зависящий от свойства материала, L — длина проводника, S — площадь поперечного сечения. Значение удельного сопротивления зависит от температуры, но при этом для каждого градуса остаётся постоянным. Его величина измерена для практически всех существующих элементов в природе и является табличной.

Открытые формулы позволили установить не только зависимость тока от сопротивления, но и связать 2 фундаментальные электрические величины — силу и работу. Причём зависимость между ними принято изображать с помощью графика, получившего название вольт-амперная характеристика. Её смысл заключается в построении функции, описывающуюся законом Ома. Это важный график для электротехнических устройств. Используя его, можно определить мощность для любых величин.

Единицы измерения

В международной системе единиц СИ единица измерения электрического сопротивления называется “ом” в честь физика Георга Ома. По определению электрическим сопротивлением 1 Ом обладает участок цепи, на котором падает напряжение 1 В при силе тока 1 А.

$$ [1 Ом] ={ [1 В]\over [1 А] } $$

Единица измерения удельного сопротивления получается производной от единиц величин, входящих в фориулу: сопротивления, длины и площади. То есть в системе СИ получатся, что если R = 1 Ом, S = 1 м2, а L = 1 м, то ρ = 1 .

Это и есть единица измерения удельного сопротивления. Но на практике оказалось, что у реальных проводов площади сечений гораздо меньше 1 м2. Поэтому было решено при вычислении ρ использовать значение площади S в мм2, чтобы итоговое значение имело компактный вид. Тогда получаются более удобные (меньше нулей после запятой) для восприятия числовые значения удельного сопротивления:

$$ [ ρ ] = { [Ом] * [мм^2] \over [м]} $$

Величину тока измеряют амперметром, а величину напряжения — вольтметром. При проведении очень точных измерений, необходимо учитывать внутреннее сопротивление этих приборов.

Измерение напряжения

Для замера напряжение используется прибор вольтметр, хотя сейчас наиболее популярны мультиметры. Мультиметр это такой комбинированный прибор имеющий в себе много чего. О нем я писал в статье и рассказывал как им пользоваться.

Вольтметр это как раз тот прибор который измеряет разность потенциалов между двумя точками. Напряжение (разность потенциалов) в любой точке схемы обычно измеряется относительно НОЛЯ или ЗЕМЛИ или МАССЫ или МИНУСА батарейки. Не важно главное это должна быть точка имеющая наименьший потенциал во всей схеме.

Итак чтобы измерить напряжение постоянного тока между двумя точками, делаем следующее. Черный (минусовой ) щуп вольтметра втыкается в ту точку, где предположительно мы можем наблюдать точку с меньшим потенциалом (НОЛЬ). Красный щуп (плюсовой) втыкаем в точку, потенциал которой нам интересен.

И результатом измерения будет числовое значение разности потенциалов, или другими словами напряжение.

Как повысить силу тока в блоке питания?

В интернете часто можно встретить вопрос, как повысить I в блоке питания, не изменяя напряжение. Рассмотрим основные варианты.

Ситуация №1.

Блок питания на 12 Вольт работает с током 0,5 Ампер. Как поднять I до предельной величины? Для этого параллельно БП ставится транзистор. Кроме того, на входе устанавливается резистор и стабилизатор.

Узнайте больше — как проверить транзистор мультиметром на исправность.

При падении напряжения на сопротивлении до нужной величины открывается транзистор, и остальной ток протекает не через стабилизатор, а через транзистор.

Последний, к слову, необходимо выбирать по номинальному току и ставить радиатор.

Кроме того, возможны следующие варианты:

• Увеличить мощность всех элементов устройства. Поставить стабилизатор, диодный мост и трансформатор большей мощности.
• При наличии защиты по току снизить номинал резистора в цепочке управления.

Ситуация №2.

Имеется блок питания на U = 220-240 Вольт (на входе), а на выходе постоянное U = 12 Вольт и I = 5 Ампер. Задача — увеличить ток до 10 Ампер. При этом БП должен остаться приблизительно в тех же габаритах и не перегреваться.

Здесь для повышения мощности на выходе необходимо задействовать другой трансформатор, который пересчитан под 12 Вольт и 10 Ампер. В противном случае изделие придется перематывать самостоятельно.

При отсутствии необходимого опыта на риск лучше не идти, ведь высока вероятность короткого замыкания или перегорания дорогостоящих элементов цепи.

Трансформатор придется поменять на изделие большего размера, а также пересчитывать цепочку демпфера, находящегося на СТОКЕ ключа.

Следующий момент — замена электролитического конденсатора, ведь при выборе емкости нужно ориентироваться на мощность устройства. Так, на 1 Вт мощности приходится 1-2 мкФ.

Также рекомендуется поменять диоды с выпрямителями. Кроме того, может потребоваться установка нового диода выпрямителя на низкой стороне и увеличение емкости конденсаторов.

После такой переделки устройство будет греться сильнее, поэтому без установки вентилятора не обойтись.

Какие бывают виды электрического тока в быту

Форма сигнала токов зависит от работы источника напряжения и сопротивления среды, через которую проходит сигнал. Чаще всего на практике домашнему мастеру приходится сталкиваться со следующим видами:

• постоянный сигнал, вырабатываемый от аккумуляторов или гальванических элементов;
• синусоидальный, создаваемый промышленными генераторами частоты 50 герц;
• пульсирующий, образуемый за счет преобразований различных блоков питания;
• импульсный, проникающий в бытовую сеть за счет разряда молний в воздушные линии электропередач;
• произвольный.

Чаще всего встречается синусоидальный или переменный ток: им питаются все наши приборы.

В современной проводке, питающейся синусоидальным напряжением, работает много полупроводниковых бытовых приборов. Они обладают не линейным сопротивлением, нарушают форму гармоники.

Эти помехи складываются по всей цепи от конкретного потребителя до питающего трансформатора, искажают идеальный синус произвольным образом. В результате изменяется как форма, так и величина питающего напряжения.

Это может привести к созданию аварийного режима: отгоранию нулевого проводника в питающей трехфазной цепи. Подробно этот процесс описан отдельной статьей другого сайта.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1= I2 ;
• U = U1+ U2 ;
• R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1+ I2 … ;
• U = U1= U2 … ;
• 1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Общие сведения

Любое физическое тело состоит из молекул и атомов. Эти частицы взаимодействуют между собой. Они могут притягиваться друг к другу или отталкиваться. В изолированной системе элементарные частицы являются носителями заряда. В спокойном состоянии, то есть когда на тело не оказывается внешнего воздействия, алгебраическая сумма энергии частиц всегда постоянная величина. Это утверждение называется законом сохранения электрического заряда.

Частицы хаотично могут перемещаться по кристаллической решётке, но их движение компенсируется. Поэтому ток не возникает. Но если к телу приложить внешнюю силу, то свободные электроны начинают двигаться в одну сторону. Это упорядоченное движение заряженных частиц и называют электрическим током. Количественно его можно описать через силу.

Упорядочено заряды заставляет двигаться электрическое поле, вдоль линий которого и происходит перемещение. Впервые этот термин ввёл Фарадей. Он сумел выяснить, что вокруг любого носителя существует особый вид материи, влияющий на поведение других частиц. За силовую характеристику электрического поля было взято отношение действующей силы к величине заряда, помещённого в данную точку: E = F / q. Назвали эту характеристику напряжённостью.

Изучение поля позволило экспериментально открыть принцип суперпозиции. То есть установить, что напряжённость поля, созданного системой зарядов, равна геометрической сумме величин, существующих у отдельных носителей: E = Σ E1 + E2 +…+ En. Напряжённость прямо пропорциональна напряжению, которое, в свою очередь, равняется разности потенциалов между двумя точками.

По сути, это работа электрического поля, совершаемая для переноса единичного заряда из одного места в другое: U = A / q = E * d, где d – расстояние между точками. Значение напряжения зависит от нескольких факторов:

• строения тела;
• температуры;
• сопротивления.

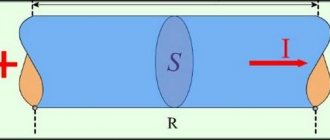
Самое большее влияние оказывает последняя величина. Именно она характеризует способность материала препятствовать прохождению тока, то есть определяет проводимость. Сопротивление зависит от длины проводника и его сечения: R = (p * l) / S, где p – параметр обратный удельной проводимости (справочное значение). Он численно равняется сопротивляемости однородного проводника единичной длины и площади сечения.

Резисторы, ток и напряжение

В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.

Представление об электричестве

Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.

Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору. Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда: — Сколько тока втекает в узел, столько из него и вытекает — Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы. — Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь. — Электрический ток будет увеличиваться при уменьшении сопротивления, как и скорость потока воды будет увеличиваться с уменьшением сопротивления клапана.

Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.

Резистор

Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах. Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания. Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего. Некоторые датчики основаны на том, что сопротивление варьируется в зависимости от освещённости, температуры или механического воздействия, об этом подробно написано в конце статьи.

Закон Ома

Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе. Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи.

Последовательное и параллельное соединение резисторов

Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:

В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой: В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:

Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет. Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути электрическому току, снижая общее сопротивление цепи.

Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R3=R1+R2

В интернете есть удобные он-лайн калькуляторы для расчета последовательного и параллельного соединения резисторов.

Токоограничивающий резистор

Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их работы, давайте сначала разберём простую схему, где лампа непосредственно подключена к 9В батареи. Лампа, как и любое другое устройство, которое потребляет электроэнергию для выполнения определенной задачи (например, светоизлучение) имеет внутреннее сопротивление, которое определяет его текущее потребление. Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.

Теперь, когда лампа будет рассматриваться как резистор, мы можем использовать закон Ома для расчета тока, проходящего через него. Закон Ома гласит, что ток, проходящий через резистор равен разности напряжений на нем, поделенное на сопротивление резистора: I=V/R или точнее так: I=(V1-V2)/R где (V1-V2) является разностью напряжений до и после резистора.

Теперь обратите внимание на рисунок выше, где добавлен токоограничительный резистор. Он будет ограничивать ток идущий к лампе, как это следует из названия. Вы можете контролировать, количество тока протекающего через лампу, просто выбрав правильное значение R1. Большой резистор будет сильно снижать ток, а небольшой резистор менее сильно (так же, как в нашей аналогии с водой).

Математически это запишется так:

Из формулы следует, что ток уменьшится, если значение R1 увеличится. Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.

Вы можете воспользоваться он-лайн калькулятором для расчета токоограничительного резистора светодиода.

Резисторы как делитель напряжения

Как следует из названия, резисторы могут быть использованы в качестве делителя напряжения, другими словами, они могут быть использованы для уменьшения напряжения путем деления его. Формула:

Если оба резистора имеют одинаковое значение (R1=R2=R), то формулу можно записать так:

Другой распространенный тип делителя, когда один резистор подключен к земле (0В), как показано на рисунке 6B. Заменив Vb на 0 в формуле 6А, получаем:

Узловой анализ

Теперь, когда вы начинаете работать с электронными схемами, важно уметь их анализировать и рассчитывать все необходимые напряжения, токи и сопротивления. Есть много способов для изучения электронных схем, и одним из наиболее распространенных методов является узловой, где вы просто применяете набор правил, и рассчитываете шаг за шагом все необходимые переменные.

Упрощенные правила узлового анализа

Определение узла

Узел – это любая точка соединения в цепи. Точки, которые связаны друг с другом, без других компонентов между ними рассматриваются как единый узел. Таким образом, бесконечное число проводников в одну точку считаются одним узлом. Все точки, которые сгруппированы в один узел, имеют одинаковые напряжения.

Определение ветви

Ветвь представляет собой набор из 1 и более компонентов, соединенных последовательно, и все компоненты, которые подсоединены последовательно к этой цепи, рассматриваются как одна ветвь.

Все напряжения обычно измеряются относительно земли напряжение на которой всегда равно 0 вольт.

Ток всегда течет от узла с более высоким напряжением на узел с более низким.

Напряжение на узле может быть высчитано из напряжения около узла, с помощью формулы: V1-V2=I1*(R1) Перенесем: V2=V1-(I1*R1) Где V2 является искомым напряжением, V1 является опорным напряжением, которое известно, I1 ток, протекающий от узла 1 к узлу 2 и R1 представляет собой сопротивление между 2 узлами.

Точно так же, как и в законе Ома, ток ответвления можно определить, если напряжение 2х соседних узлах и сопротивление известно: I 1=(V1-V2)/R1

Текущий входящий ток узла равен текущему выходящему току, таким образом, это можно записать так: I 1+ I3=I2

Важно, чтобы вы были в состоянии понимать смысл этих простых формул. Например, на рисунке выше, ток протекает от V1 до V2, и, следовательно, напряжение V2 должно быть меньше, чем V1. Используя соответствующие правила в нужный момент, вы сможете быстро и легко проанализировать схему и понять её. Это умение достигается практикой и опытом.

Расчет необходимой мощности резистора

При покупке резистора вам могут задать вопрос: «Резисторы какой мощности вы хотите?» или могут просто дать 0.25Вт резисторы, поскольку они являются наиболее популярными. Пока вы работаете с сопротивлением больше 220 Ом, и ваш блок питания обеспечивает 9В или меньше, можно работать с 0.125Вт или 0.25Вт резисторами. Но если напряжение более 10В или значение сопротивления менее 220 Ом, вы должны рассчитать мощность резистора, или он может сгореть и испортить прибор. Чтобы вычислить необходимую мощность резистора, вы должны знать напряжение через резистор (V) и ток, протекающий через него (I): P=I*V где ток измеряется в амперах (А), напряжение в вольтах (В) и Р — рассеиваемая мощность в ваттах (Вт)

На фото предоставлены резисторы различной мощности, в основном они отличаются размером.

Разновидности резисторов

Резисторы могут быть разными, начиная от простых переменных резисторов (потенциометров) до реагирующих на температуру, свет и давление. Некоторые из них будут обсуждаться в этом разделе.

Переменный резистор (потенциометр)

На рисунке выше показано схематическое изображение переменного резистора. Он часто упоминается как потенциометр, потому что он может быть использован в качестве делителя напряжения.

Они различаются по размеру и форме, но все работают одинаково. Выводы справа и слева эквивалентны фиксированной точке (например, Va и Vb на рисунке выше слева), а средний вывод является подвижной частью потенциометра, а также используется для изменения соотношения сопротивления на левом и правом выводах. Следовательно, потенциометр относится к делителям напряжения, которым можно выставить любое напряжение от Va к Vb. Кроме того, переменный резистор может быть использован как тока ограничивающий путем соединения выводов Vout и Vb, как на рисунке выше (справа). Представьте себе, как ток будет течь через сопротивление от левого вывода к правому, пока не достигнет подвижной части, и пойдет по ней, при этом, на вторую часть пойдет очень мало тока. Таким образом, вы можете использовать потенциометр для регулировки тока любых электронных компонентов, например лампы.

LDR (светочувствительные резисторы) и термисторы

Есть много датчиков основанных на резисторах, которые реагируют на свет, температуру или давление. Большинство из них включаются как часть делителя напряжения, которое изменяется в зависимости от сопротивления резисторов, изменяющегося под воздействием внешних факторов.

Фоторезистор (LDR)

Как вы можете видеть на рисунке 11A, фоторезисторы различаются по размеру, но все они являются резисторами, сопротивление которых уменьшается под воздействием света и увеличивается в темноте. К сожалению, фоторезисторы достаточно медленно реагируют на изменение уровня освещённости, имеют достаточно низкую точность, но очень просты в использовании и популярны. Как правило, сопротивление фоторезисторов может варьироваться от 50 Ом при солнце, до более чем 10МОм в абсолютной темноте.

Как мы уже говорили, изменение сопротивления изменяет напряжение с делителя. Выходное напряжение можно рассчитать по формуле:

Если предположить, что сопротивление LDR изменяется от 10 МОм до 50 Ом, то Vout будет соответственно от 0.005В до 4.975В.

Термистор похож на фоторезистор, тем не менее, термисторы имею гораздо больше типов, чем фоторезисторы, например, термистор может быть либо с отрицательным температурным коэффициентом (NTC), сопротивление которого уменьшается с повышением температуры, или положительным температурным коэффициентом (PTC), сопротивление которого будет увеличиваться с повышением температуры. Сейчас термисторы реагируют на изменение параметров среды очень быстро и точно.

Схемотехническое обозначение резисторов

Про определение номинала резистора используя цветовую маркировку можно почитать здесь.

Оригинал статьи

Теги:

• Перевод