Идеальный источник напряжения
Идеальные источники тока и напряжения представляют собой идеализированные источники энергии. Они обладают способностью отдавать энергию подключенным к ним участкам электрической цепи, другими словами, потребляемая ими энергия может быть отрицательной. Таким образом, идеальные источники тока и напряжения относятся к идеализированным активным элементам.
Идеальный источник напряжения (источник напряжения, источник э. д. с. ) представляет собой идеализированный активный элемент, напряжение на зажимах которого не зависит от протекающего через него тока. Напряжение и на зажимах источника напряжения равно электродвижущей силе е (t) и может быть произвольной функцией времени. В частном случае е (t) = Е_ может не зависеть от времени. Источник такого типа называется источником постоянного напряжения (источником постоянной э. д. с.). Условное графическое обозначение источника напряжения приведено на рис. 1.12, а. Стрелка внутри кружка на рисунке указывает направление э. д. с. Для источников постоянного напряжения она направлена от зажима с меньшим потенциалом к зажиму с более высоким потенциалом, в то время как напряжение на внешних зажимах источника направлено от зажима с более высоким потенциалом к зажиму с меньшим потенциалом.
Внешней характеристикой любого источника электрической энергии называется зависимость напряжения на его зажимах 01 тока источника. Внешняя характеристика источника постоянного напряжения является прямой линией, параллельной оси токов (Рис. 1.12, б).
Если подключить к зажимам источника э. д. с. сопротивление нагрузки
С уменьшением ток нагрузки и выделяемая в ней мощность неограниченно возрастают. Вследствие этого источник напряжения иногда называют источником бесконечной мощности.
Режимы работы источника Э.Д.С.
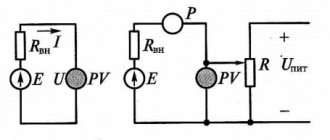
Рис.3.5. Схема реального источника ЭДС с нагрузкой.
Режим холостого хода (ключ S разомкнут) (рис 3.5). Напряжение холостого хода на выходе источника равно его ЭДС (UХХ = E), ток холостого хода равен нулю (IХХ = 0), т.к. сопротивление нагрузки равно бесконечности (RН = ¥), коэффициент полезного действия (К.П.Д.) при идеальном источнике ЭДС в этом режиме стремится к единице (h = 1).
1. Номинальный режим – это режим, на который рассчитывается источник, (ключ S замкнут). В этом режиме источник Е работает эффективно с точки зрения надёжности и экономичности
IН = IНОМ = , UВЫХ = UНОМ,
h =
< 1.
2. Согласованный режим — режим, при котором в нагрузку отдаётся максимальная мощность.
Мощность источника: P
И=
E×I
Мощность нагрузки: P
Н=
U
НАГР×
I
НАГР
I
НАГР = ,
U
НАГР =
I
НАГР
R
Н =
R
Н,
следовательно
P
Н =
U
НАГР×
I
НАГР =
R
Н
I
2НАГР = ( )2
R
Н.
Вопрос: «При какой величине RН мощность в нагрузке будет иметь максимальное значение?», т.е. нужно определить экстремум функции PН(RН). Для этого возьмем производную от выражения P
н=
R
н·
I
2=
E
2·
R
/(
R
+
R
)2.
Максимальное значение мощности будет при =0. Это будет при Rн=Rвн .
К.П.Д: h=Pн/Pи=E2×R/(Rвн+Rн)2×(Rвн+Rн)/E2=Rн/(Rн+Rвн) =1/(1+Rвн/Rн)
Таким образом в согласованном режиме
Pнапр=Pmax=Pист/2; Uн=E/2; Iн=Iк.з/2; Rн=Rвн; h
=0.5
4. Режим короткого замыкания – режим, при сопротивлении нагрузки равном нулю.
В этом режиме: Rн=0, Uн=0, Iкз =E/Rвн, h=0, Pист= Pвн= Iкз× E, Pн=0.
Рис. 3.6. Зависимость мощностей: источника, приемника и потерь от тока.
Как видно из рис 3.6 мощность потерь представляет собой параболу в соответствии с формулой Pвн= RвнI2
, а мощность источника – прямую линию в соответствии с формулой
Pи= EI
, тогда мощность нагрузки в соответствии с балансом мощностей
Pи= Pвн+Pн
, будет иметь вид перевёрнутой параболы, т.к.
Pн= Pи-Pвн
.
Баланс мощностей, определение – «Сумма мощностей источников равна сумме мощностей приёмников и мощностей потерь».
Рис. 3.7. Внешняя характеристика реального источника Э.Д.С.
Внешняя характеристика реального источника ЭДС представляет собой падающую прямую линию в соответствии с формулой второго закона Кирхгофа Uн=E-Uвн=E-RвнI
. Падение напряжения на внутреннем сопротивлении представляет собой растущую прямую линию
Uвн=RвнI
.
| Rн |
| Uвн |
| Uн |
| Uн |
| Uвн |
| Iн |
| Iн |
| E |
| E |
| E |
| Rвн |
| E |
Рис. 3.8. Зависимость падений напряжений на источнике, приемнике и тока от величины сопротивления нагрузки.
На рис. 3.8 приведены зависимости падений напряжений на источнике, приемнике и тока от величины сопротивления нагрузки. Как видно эти зависимости имеют вид гиперболы. Действительно, в формуле Eи R
вн —
постоянные величины, а R
н
– величина переменная, значит это уравнение гиперболы. График падения напряжения на внутреннем сопротивлении тоже представляет собой гиперболу, т.к. по закону Ома Uвн=RвнIн , Rвн —
величина постоянная, а график Iн(Rн) –
гипербола, значит и
Uвн(Rвн) тоже – гипербола.
Вопросы по теме лекции.
1. Условие эквивалентности схем.
2. Эквивалентное сопротивление при последовательном сопротивлении оных, схема, формула.
3. Эквивалентное сопротивление при параллельном сопротивлении оных, схема, формула.
4. Преобразование реального источника ЭДС в эквивалентный источник тока. Схема, формула.
5. Преобразование реального источника тока в эквивалентный источник ЭДС. Схема, формула.
6. Преобразование треугольника сопротивлений в эквивалентную звезду, схемы, формулы.
7. Преобразование сопротивлений, собранных по схеме «звезда» в эквивалентный треугольник, схемы, формулы.
8. Теорема об эквивалентном генераторе (Гельмгольца – Те Ве Нена), сема формула.
9. Теорема об эквивалентном источнике тока (Нортона).
10. Режимы работы источника ЭДС (типы).
11. Холостой ход источника ЭДС, схема, условия проведения, для чего проводится.
12. Номинальный режим работы источника ЭДС, определение, формулы падения напряжения: на нагрузке, на внутреннем сопротивлении.
13. Номинальный режим работы источника ЭДС, определение, формулы тока и кпд.
14. Номинальный режим работы источника ЭДС, определение, формулы мощностей: источника, приёмника, потерь.
15. Баланс мощностей, определение, формула.
16. Согласованный режим работы источников ЭДС, где применяется.
17. Условие наступления согласованного режима работы, доказательство.
18. Режим короткого замыкания ЭДС, ток короткого замыкания, формула.
19. Зависимости мощностей и кпд от тока, формулы, подтверждающие вид этих графиков.
20. Зависимости ЭДС, падения напряжений на нагрузке и на внутреннем сопротивлении от тока, формулы, подтверждающие вид этих графиков.
21. Зависимости ЭДС, тока, падения напряжений на внутреннем сопротивлении и на нагрузке от величины сопротивления нагрузки.
Лекция 4.
⇐ Предыдущая3Следующая ⇒
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все…
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор…
Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право…
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? — задался я вопросом…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Идеальный источник тока
Идеальный источник тока (источник тока) — это идеализированный активный элемент, ток которого не зависит от напряжения на его зажимах. Ток источника i=j(t) может быть произвольной функцией времени, в частном случае он может не зависеть от времени i(t) = J_ (источник постоянного тока). Внешняя характеристика источника постоянного тока показана на рис. 1.14, б.
Условное графическое обозначение источника тока приведено на рис. 1.14, а. Двойная стрелка на рисунке показывает направление тока внутри источника. У источников постоянного тока это направление совпадает с направлением перемещения положительных зарядов внутри источника, т. е. с направлением от зажима с меньшим потенциалом к зажиму с большим потенциалом.
Ток источника тока и напряжение источника напряжения являются параметрами идеализированных активных элементов подобно тому, как сопротивление, емкость и индуктивность являются параметрами одноименных идеализированных пассивных элементов.
Если подключить к внешним выводам источника тока сопротивление нагрузки (рис. 1.15), то согласно (1.9), (1.11) напряжение на сопротивлении нагрузки и выделяемая в нагрузке мощность будут равны соответственно:
С увеличением напряжение на нагрузке и выделяемая в ней мощность неограниченно увеличиваются, поэтому источник тока, так же как и источник напряжения, является источником бесконечной мощности).
Зависимость тока источника тока от напряжения имеет такой же вид, как и зависимость напряжения источника напряжения от тока, поэтому эти источники являются дуальными элементами.
Реактивное внутреннее сопротивление
Полное сопротивление
Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.
На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
Схемы замещения реальных источников
Идеализированные источники тока и напряжения можно рассматривать как упрощенные модели реальных источников энергии. При определенных условиях, в достаточно узком диапазоне токов и напряжений, внешние характеристики ряда реальных источников энергии могут приближаться к характеристикам идеализированных активных элементов. Так, внешняя характеристика гальванического элемента в области малых токов имеет вид, близкий к внешней характеристике источника напряжения (см. рис. 1.12,6), а внешняя характеристика выходного каскада на транзисторе в определенном диапазоне напряжений приближается к внешней характеристике источника тока (см рис. 1.14,6).
В то же время свойства реальных источников энергии значительно отличаются от свойств идеализированных активных элементов. Реальные источники энергии обладают конечной мощностью; их внешняя характеристика, как правило, не параллельна оси токов или оси напряжений, а пересекает эти оси в двух характерных точках, соответствующих режимам холостого хода и короткого замыкания (иногда в источниках энергии применяют специальные виды защиты, исключающие работу в предельных режимах или в одном из них).
С достаточной для практики точностью внешние характеристики большинства реальных источников энергии могут быть приближенно представлены прямой линией, пересекающей оси токов и напряжений в точках 1 и 2 (рис. 1.16, а):
соответствующих режимам холостого хода и короткого замыкания источника. Источники, имеющие линейную внешнюю характеристику, в дальнейшем будем называть линеаризованными источниками энергии (реальными).
Покажем, что линеаризованный источник энергии может быть представлен моделирующей цепью, состоящей из идеализированного источника напряжения Е и внутреннего сопротивления или идеализированного источника тока J и внутренней проводимости Действительно, уравнение прямой, проходящей через две точки с координатами имеет вид
Подставляя (1.28), (1.29) в (1.30) и представляя напряжение u как функцию тока i, находим аналитическое выражение для внешней характеристики линеаризованного источника
В соответствии с (1.31) напряжение линеаризованного источника состоит из двух составляющих. Первая их имеет размерность напряжения и не зависит от тока, протекающего через источник. Ее можно интерпретировать как напряжение некоторого идеального источника напряжения с э. д. с. Вторая составляющая напряжения источника прямо пропорциональна току. Ее можно рассматривать как падение напряжения на некотором сопротивлении через которое протекает ток источника i (это сопротивление в дальнейшем будем называть внутренним сопротивлением источника). Итак, уравнению (1.31) может быть поставлена в соответствие схема замещения линеаризованного источника, изображенная на рис. 1.16,б. Такая схема замещения получила название
последовательной. Можно убедиться, что зависимость напряжения на зажимах этой цепи от тока определяется уравнением
равносильным уравнению (1.31) и, следовательно, внешняя характеристика цепи имеет вид, показанный на рис. 1.16, а.
Из анализа выражения (1.32) видно, что с уменьшением внутреннего сопротивления источника внешняя характеристика линеаризованного источника приближается к внешней характеристике идеального источника напряжения (рис. 1.17, а). При = 0 источник с линейной внешней характеристикой вырождается в идеальный источник напряжения. Таким образом, идеальный источник напряжения можно рассматривать как источник энергии, внутреннее сопротивление которого равно нулю.
Рассмотрим другую схему замещения линеаризованного источника, в которой содержится идеальный источник тока. Для этого, используя (1.31), выразим ток i как функцию напряжения на зажимах источника:
Как видно из выражения (1.33), ток линеаризованного источника состоит из двух составляющих. Первая не зависит от напряжения на зажимах источника. Ее можно рассматривать как ток некоторого идеального источника тока Вторая составляющая тока и прямо пропорциональна напряжению на зажимах источника, поэтому ее можно интерпретировать как ток, текущий через некоторую (внутреннюю) проводимость к которой приложено напряжение u. Итак, выражению (1.33) можно поставить в соответствие схему замещения, изображенную на рис. 1.16, в. Такая схема замещения называется параллельной.
Зависимость между током и напряжением на зажимах соответствующей моделирующей цепи определяется уравнением, равносильным уравнению (1.33):
Из уравнения (1.34) видно, что с уменьшением внутренней проводимости источника внешняя характеристика линеаризованного источника приближается к внешней характеристике идеального источника тока (рис. 1.17, б). В пределе, при = 0, линеаризованный источник энергии вырождается в идеальный источник тока. Таким образом, идеальный источник тока можно рассматривать как источник энергии с бесконечно малой внутренней проводимостью (бесконечно большим внутренним сопротивлением).
Обе рассмотренные схемы замещения линеаризованного источника были получены из одного уравнения (1.30), имеют одну и ту же внешнюю характеристику и, следовательно, их поведение относительно внешних зажимов совершенно одинаково. Выбор той или иной схемы замещения может быть сделан совершенно произвольно, однако в процессе исследования цепи может возникнуть необходимость перехода от одной схемы к другой. Используя выражения (1.31)—(1.34), можно найти формулы перехода от последовательной схемы замещения к параллельной
и от параллельной схемы к последовательной
Необходимо обратить внимание на то, что переход от одной схемы замещения к другой возможен только для источников, внутреннее сопротивление которых имеет конечное значение
Соотношения для взаимного преобразования схем замещения источников энергии (1.35) и (1.36) применимы для источников постоянного тока и напряжения. Аналогичные соотношения могут быть получены и для источников, в которых напряжение u и ток i являются произвольными функциями времени.
Анализируя выражения (1 32), (1.34), можно установить, что цепь, составленная из источника напряжения с последовательно включенным сопротивлением и цепь, представляющая собой параллельное соединение источника тока и проводимости являются дуальными.
Виды источников электрического тока
Существуют следующие виды источников электрического тока:
- механические;
- тепловые;
- световые;
- химические.
Механические источники
В этих источниках происходит преобразование механической энергии в электрическую. Преобразование осуществляется в специальных устройствах – генераторах. Основными генераторами являются турбогенераторы, где электрическая машина приводится в действие газовым или паровым потоком, и гидрогенераторы, преобразующие энергию падающей воды в электричество. Большая часть электроэнергии на Земле производится именно механическими преобразователями.
Тепловые источники
Здесь преобразуется в электричество тепловая энергия. Возникновение электрического тока обусловлено разностью температур двух пар контактирующих металлов или полупроводников — термопар. В этом случае заряженные частицы переносятся от нагретого участка к холодному. Величина тока зависит напрямую от разности температур: чем больше эта разность, тем больше электрический ток. Термопары на основе полупроводников дают термоэдс в 1000 раз больше, чем биметаллические, поэтому из них можно изготавливать источники тока. Металлические термопары используют лишь для измерения температуры.
СПРАВКА! Чтобы получить термопару, необходимо соединить 2 различных металла.
В настоящее время разработаны новые элементы на основе преобразования тепла, выделяющегося при естественном распаде радиоактивных изотопов. Такие элементы получили название радиоизотопный термоэлектрический генератор. В космических аппаратах хорошо себя зарекомендовал генератор, где применяется изотоп плутоний-238. Он даёт мощность 470 Вт при напряжении 30 В. Так как период полураспада этого изотопа 87,7 года, то срок службы генератора очень большой. Преобразователем тепла в электричество служит биметаллическая термопара.