AudioKiller’s site
Обратная связь – процесс передачи сигнала с выхода усилителя обратно на его вход, а также цепь, осуществляющая эту передачу.
Обратная связь (ОС) называется отрицательной (ООС, NFB), если выходной сигнал усилителя вычитается из входного. Для простоты будем рассматривать установившийся режим работы всей системы, причем усилитель работает в активном режиме (т.е. нормально усиливает сигнал без всяких там перегрузок).
Структурная схема усилителя, охваченного ООС, показана на рис.1.
Рис. 1. Структурная схема усилителя, охваченного ООС.
Здесь некоторый «виртуальный» усилитель с коэффициентом усиления по напряжению Ku’ получается из исходного «реального» усилителя, имеющего коэффициент усиления Ku, и охваченного цепью ООС. На самом деле термин «виртуальный» не совсем корректен, но я буду пользоваться им, потому что с точки зрения внешних устройств, подключенных к системе в целом, она представляет собой усилитель с параметрами, отличающимися от параметров реального исходного усилителя без ООС.
С выхода реального усилителя напряжение передается на его вход через цепь ООС с коэффициентом передачи β:
Обычно цепь ООС является пассивной, и β ≤ 1. Если цепь ООС усиливает, то это принципиально ничего не меняет, и все формулы в этом случае выводятся аналогично. Если β = 0, то это означает, что Uоос = 0 и обратная связь отсутствует. Обратите внимание, что совершенно безразлично, какую именно схему имеет цепь ООС. Главное – это насколько (во сколько раз) она ослабляет напряжение.
В данной системе присутствует два разных входных напряжения, и чтобы не путаться, я им дам различные наименования:
1. Напряжение, подаваемое на вход «виртуального» усилителя от источника сигнала. Его будем обозначать Uсигн.
2. Напряжение, приходящее на вход реального усилителя – Uвх.
Итак, выходное напряжение усилителя Uвых превращается цепью ООС в напряжение обратной связи Uоос и вычитается из входного напряжения. Результат – входное напряжение реального усилителя:
Важный момент: Uоос всегда меньше Uсигн, поэтому Uвх всегда больше нуля.
Реальный усилитель усиливает свой входной сигнал в Ku раз:
Преобразуем формулу (3):
Но Uвых/Uсигн – это коэффициент усиления Ku’ «виртуального» усилителя, как он проявляется для внешнего мира, поэтому:
Таким образом, мы получили формулу для вычисления коэффициента усиления для усилителя, охваченного ООС.
Теперь можно объяснить, почему Uоос <� Uсигн. Допустим, что Uоос = Uсигн. Тогда напряжение, приходящее на вход реального усилителя равно нулю: Uвх = Uсигн – Uоос = 0. А раз так, то и выходное напряжение усилителя равно нулю: Uвых = Uвх∙Ku. Но ведь Uоос получается из выходного напряжения: Uоос = Uвых∙β, значит оно также будет равно нулю! Пришли к противоречию: предположив, что Uоос = Uсигн, получили, что Uоос = 0. Так происходит только при отсутствии сигнала на входе всей системы, когда все напряжения равны нулю. Что будет, если Uоос > Uсигн, рассмотрите самостоятельно. С точки зрения математики, исходное утверждение доказывается элементарно:
Рассматривая физику процессов, следует помнить, что выходное напряжение усилителя появляется не само по себе, а является следствием его усиления и образуется из его входного напряжения: Uвых = Ku∙Uвх.
Итак, при охвате усилителя ООС, его коэффициент усиления уменьшается в (1+β∙Ku) раз. Но введение ООС изменяет и другие параметры усилителя.
1. Отрицательная обратная связь изменяет в (1+β∙Ku) раз входное и выходное сопротивления усилителя. При этом они могут как увеличиваться, так и уменьшаться в зависимости от способа соединения цепи ООС со входом и выходом усилителя – последовательно или параллельно. Способы подключения цепи ООС ко входу усилителя показаны на рис. 2, а к выходу усилителя – на рис. 3.
Рис. 2. Способы подключения цепи ООС ко входу усилителя.
Эти формулы несложно вывести, но мы это делать не будем, а будем пользоваться готовыми. И объяснить их с точки зрения схемотехники также несложно. Например, на рис. 2а, напряжение на входе усилителя после замыкания цепи ООС возросло в (1+β∙Ku) раз: Uсигн = Uвх∙(1+β∙Ku), а входной ток остался прежним. Значит, по закону Ома (R=U/I) и сопротивление возросло в (1+β∙Ku) раз.
Рис. 3. Способы подключения цепи ООС к выходу усилителя.
При последовательной по выходу ООС через ее цепь проходит выходной ток усилителя (ток нагрузки), поэтому ее часто называют обратной связью по току. Несколько примеров разных включений цепи ООС показано на рис. 4 и рис. 5. Цепь ООС является четырехполюсником, который обычно замыкается через «землю» цепи, явным образом это показано на рис. 4б.
Рис. 5. Примеры включения цепи ООС в усилителе на ОУ.
2. Отрицательная обратная связь расширяет частотный диапазон усилителя. Нижняя fн и верхняя fв граничные частоты увеличиваются примерно в (1+β∙Ku), если усилитель имеет спад АЧХ 6 дБ/октаву. На самом деле, при охвате усилителя ООС могут происходить самые разные процессы, вплоть до превращения усилителя в генератор, но если все работает, то частотный диапазон обязательно расширяется. Это иллюстрируют АЧХ исходного усилителя (синяя) и усилителя, охваченного ООС (красная) на рис. 6. Там же показаны границы частотного диапазона без ООС и с ней. Напоминаю, что граничной частотой считается такая частота, где коэффициент усиления уменьшается в корень из двух (примерно 1,41) раз.
Рис. 6. Расширение частотного диапазона при помощи ООС.
3. Введение ООС уменьшает нелинейные искажения усилителя (коэффициент гармоник) примерно в (1+β∙Ku) раз. Это происходит оттого, что ООС линеаризует систему и уменьшает ее ошибки. Изменяется и амплитудная характеристика усилителя (рис.7), на ней плавный переход к области насыщения превращается в довольно острый излом – ООС линеаризует этот участок и «пытается» вытянуть пропорциональное усиление даже там, где оно уже начинает уменьшаться.
Рис. 7. Улучшение линейности усилителя при помощи ООС.
На самом деле (1+β∙Ku) – это очень приблизительная оценка, поскольку для анализа нелинейных цепей используется уже совсем другая математика и там все очень сильно зависит от нелинейности усилителя. Но, тем не менее, искажения усилителя снижаются тем сильнее, чем глубже ООС, и в «простых» случаях формула (1+β∙Ku) работает достаточно хорошо.
Итак, мы видим, что охват усилителя отрицательной обратной связью изменяет ряд его основных параметров в (1+β∙Ku) раз. Проанализируем это выражение сначала чисто математически, не вникая пока в его физический смысл. Очевидно, что тут возможны три варианта:
а) β∙Ku << 1 и это слагаемое практически не влияет на результат. Это происходит при очень малой глубине ООС.
б) β∙Ku ≈ 1. В этом случае можно считать, что глубина ООС становится достаточно большой, чтобы начать оказывать влияние на параметры усилителя.
г) β∙Ku >> 1. Тут обратная связь очень глубока. Интересно, что для очень глубокой ООС формула (4) превращается вот во что:
То есть, свойства усилителя (коэффициент усиления и АЧХ) определяются исключительно параметрами цепи ООС. При значении β∙Ku = 100, погрешность применения вместо формулы (4) упрощенной формулы (5) составляет 1%, такой погрешностью в большинстве случаев можно пренебречь. А в реальных схемах на операционных усилителях величина β∙Ku может достигать десятков тысяч, делая погрешность «упрощения формулы» практически незначимой.
Обратите внимание, что в формуле присутствует величина β∙Ku, как произведение. При этом одинаковое значение этого произведения можно получить как при большой величине Ku и маленьком β, так и при большом β и небольшом Ku, так что в данном смысле эти два параметра равнозначны. Термин «глубина обратной связи» часто ассоциируется с термином «коэффициент передачи цепи ООС», который обозначает величину β, а хорошо было бы ввести некоторое понятие, отражающее именно величину β∙Ku, как более важную для применения. Так сейчас и поступим, только не забывайте, что у нас β ≤ 1, так что понятие большое или маленькое β означает, например, такие значения: β = 0,1 или β = 0,0001.
Теперь давайте оценим степень влияния отрицательной обратной связи, исходя из физического смысла и электроники. Обратимся к рис. 1. Внутри усилителя присутствует два напряжения: Uвх и Uоос. Очевидно, что степень влияния ООС на усилитель зависит от соотношения этих напряжений. Если Uоос <<� Uвх, то сигнал обратной связи незначителен на фоне входного сигнала усилителя, и ООС влияет слабо. И наоборот, если Uоос >> Uвх, то главную роль во входном сигнале «реального» усилителя играет именно ООС (т.к. Uсигн = Uоос + Uвх и значит входной сигнал «виртуального» усилителя практически равен Uоос). С другой стороны, Uоос получается из напряжения Uвх, после усиления его усилителем и ослабления цепью ООС. Как оно получается? Мысленно разомкнем петлю обратной связи в точке А (разрывать цепь электрически можно не всегда – иногда от этого изменяется величина β), рис. 8.
Рис. 8. Разомкнутая петля ООС.
Со стороны точки приложения сигнала ООС (это точка А), входной сигнал проходит два элемента – усилитель и цепь ООС. Общий коэффициент передачи последовательно соединенных устройств равен произведению их коэффициентов передачи: Ku∙β. Эта величина является коэффициентом усиления сигнала в петле обратной связи и называется петлевым усилением:
С другой стороны:
Это то самое взаимоотношение между напряжением ООС и входным напряжением «реального» усилителя, которое показывает степень влияния обратной связи. Кроме того, оно полностью соответствует выражению, которое мы вывели, математически анализируя формулу коэффициента усиления усилителя с замкнутой ООС. Так что глубину обратной связи характеризует именно петлевое усиление, и именно его имеют ввиду, когда говорят о глубине ООС. Хотя иногда под глубиной ООС подразумевают коэффициент передачи цепи обратной связи β – в случаях, когда Ku велико, и величину A = β∙Ku определяет в основном β.
Таким образом, именно петлевое усиление определяет свойства усилителя, которые он проявляет для внешнего мира. Именно на эту величину изменяются коэффициент усиления, входное и выходное сопротивления, граничные частоты и коэффициент гармоник.
В некоторых случаях вычисление петлевого усиления по формуле (6) может быть затруднено, тогда можно найти его из изменения коэффициента усиления усилителя при охвате его ООС:
Последнее выражение достаточно точно, при А≥100. Проще всего определять таким способом петлевое усиление по логарифмической АЧХ усилителя (диаграмме Боде). На рис. 9 петлевое усиление А = 100 – 60 = 40 дБ, т.е. 100 раз. На самом деле А = 100 – 1 = 99 раз (39,9 дБ), но этим зачастую можно пренебречь, поэтому обычно в таких случаях говорят, что петлевое усиление равно ровно 40 дБ.
Рис. 9. Определение глубины ООС по АЧХ.
Пока что я ничего не говорил о свойствах и схеме самой цепи ООС. На самом деле, значение ее коэффициента передачи не обязательно являются константой. Эта цепь может быть частотнозависимой, тогда величина β меняется с частотой. Такое свойственно современным усилителям сигналов, когда для постоянного тока стремятся получить стопроцентную обратную связь (β=1), дающую максимальную стабильность режима работы усилителя, а для переменного тока глубину ООС выбирают такой, чтобы Ku’ для него (усиливаемого сигнала) был равен 10…1000 (β≈0,1…0,001). На самом деле при снижении частоты f ниже определенного значения, β начинает расти, доходя до единицы при f = 0, т.е. на постоянном токе. Но это все происходит ниже рабочего диапазона частот усилителя, поэтому в таких случаях глубину ООС принято оценивать двумя значениями: для постоянного тока, и для переменного тока (в рабочем диапазоне частот).
Если вернуться к формуле (5) для коэффициента усиления с замкнутой цепью ООС, то видно, что при достаточно большом значении петлевого усиления, свойства усилителя – это обратная величина от свойств цепи обратной связи. Такая ситуация лучше всего получается, если усилитель имеет очень большой коэффициент усиления без ООС – десятки-сотни тысяч и миллионы. Для работы в таких условиях созданы специальные микросхемы, называемые операционными усилителями (ОУ).
Понятие операционного усилителя появилось во второй половине ХХ века, когда получили широкое распространение аналоговые электронно-вычислительные машины (АВМ). Принцип их применения был основан на том, что подбиралась соответствующая электрическая цепь, описываемая теми же уравнениями, что и исследуемый неэлектрический процесс. Измеряя напряжения и токи в цепи, получали значения параметров исследуемого процесса. Для АВМ требовались блоки (функциональные узлы), выполняющие определенные математические операции: масштабирование (усиление), сложение, вычитание, интегрирование, дифференцирование и др. Довольно быстро пришли к выводу, что вместо того, чтобы разрабатывать каждый такой блок по-отдельности, проще получить их все из одинаковых усилителей, охваченных цепью ООС – так и появились ОУ. В настоящее время возможности цифровых вычислительных машин настолько велики, что моделирование (и управление) проще и точнее выполнять на них, и АВМ практически исчезли, а операционные усилители остались – они оказались очень удобными для применения, ведь из них можно получить практически любое устройство, всего лишь охватив их соответствующей ООС.
Так что получить, например, усилитель с нужной АЧХ достаточно просто, достаточно охватить его ООС, имеющей АЧХ «зеркальной» к требуемой (рис. 10).
Рис. 10. Частотнозависимая ООС.
Схемы, реализующие данные АЧХ показаны на рис. 11.
Рис. 11. Цепь частотнозависимой ООС.
Однако, конструируя схемы на операционных усилителях, следует помнить, что их огромный коэффициент усиления сохраняется только на очень низких частотах, а потом начинает падать со скоростью 20 дБ/декада. У большинства ОУ широкого применения спад АЧХ начинается с частоты порядка 10 Гц. Поэтому на частотах в десятки килогерц Ku может быть довольно мал, и при попытке получить на такой частоте большое усиление, глубина обратной связи (петлевое усиление) может оказаться слишком маленьким. При этом возрастет погрешность выполняемой функции, и повышаются нелинейные искажения. На рис. 12 показаны АЧХ усилителя (см. рис. 10 и рис. 11) без ООС и с ООС. На частотах 20 Гц, 1 кГц и 20 кГц глубина ООС (петлевое усиление) составляет 39 дБ, 24 дБ и 11 дБ соответственно. Вполне можно считать, что на частоте 20 кГц обратная связь имеет очень низкую глубину и практически не улучшает параметров усилителя.
Рис. 12. Зависимость глубины ООС от частоты.
В заключение хотелось бы отметить, что это только элементарная теория обратной связи. Здесь, например, не учтен тот факт, что на переменном токе и коэффициент усиления «реального» усилителя, и коэффициент передачи цепи обратной связи обычно величины комплексные (петлевое усиление также является комплекным). Поэтому формула (4) верна только для модулей, а «на все случаи жизни» ее надо записывать так:
При этом цепь ООС может изменять не только амплитуду сигнала, но и его фазу. Причем, если сдвиг фаз в петле ООС станет равным 180 градусам, то сигнал обратной связи будет не вычитаться из сигнала источника, а прибавляться к нему, и обратная связь из отрицательной превратится в положительную. Но это уже совсем другая история…
Главная цель этого материала – дать понимание основ обратной связи для дальнейшего углубленного ее изучения, тем более что физика и математика процессов показана совершенно правильно.
Готовлю продолжение о секретах применения отрицательной обратной связи.
23.11.2010
Total Page Visits: 13461 — Today Page Visits: 8
Нестабильность правой полуплоскости
В топологиях, где выходной дроссель работает с непрерывным током через диод, — например, в повышающих, повышающе-понижающих, обратноходовых и прямоходовых преобразователях, — время проводимости диода добавляет задержку в цепи обратной связи. Это связано с тем, что когда нагрузка резко возрастает, то для передачи большей энергии в катушку индуктивности рабочий цикл должен быть временно увеличен. Тем не менее рабочий цикл большой длительности приводит к уменьшению времени проводящего состояния (tOFF) диода, так что средний ток через диод во время tOFF фактически уменьшается (рис. 9, справа). По мере того как выходной ток протекает через диод, этот ток также уменьшается. Данное условие сохраняется до тех пор, пока средний ток дросселя медленно увеличивается, а ток диода достигает заданного значения.
Рис. 9. Феномен правой полуплоскости
Это явление, когда ток через диод должен сначала уменьшиться, прежде чем он станет увеличиваться, известен как нестабильность правой полуплоскости (англ. Right Half Plane instability или RHP instability), потому что выходной ток временно находится в противофазе с рабочим циклом. Например, в простом повышающем преобразователе (рис. 10) частота временного дополнительного нуля находится в соответствии с выражением:
Рис. 10. Повышающий импульсный стабилизатор, упрощенная схема
RHP-нестабильность практически невозможно компенсировать, поскольку этот ноль изменяется еще и с током нагрузки. Решение состоит в том, чтобы выбрать параметры петли обратной связи с частотой среза существенно ниже самой низкой частоты появления RHP нулей (это имеет определенный недостаток, поскольку приводит к ухудшению времени реакции DC/DC-преобразователя на ступенчатое изменение нагрузки). Для того чтобы устранить подобную проблему в целом, необходимо использовать понижающе-повышающий преобразователь в режиме прерывистых токов (режим DCM).
Определение стабильности петли обратной связи с использованием преобразования Лапласа
Альтернативой экспериментальному методу определения стабильности является математическое вычисление нулей и полюсов. Для этого нам необходимо знать передаточную функцию преобразователя.
Для простого понижающего преобразователя, показанного на рис. 1, передаточная функция равна:
Параметр, обозначенный как s, здесь указывает на то, что переменная передаточной функции имеет частотную зависимость. Передаточная функция может быть решена с помощью преобразования Лапласа, но для того, чтобы понять это преобразование, сначала нужно рассмотреть преобразование Фурье.
Преобразование Фурье — это особая форма преобразования Лапласа. Фурье установил, что любой периодический сигнал является суммой синусоидальных сигналов различной частоты, фазы и амплитуды (ряд Фурье). Преобразование представляет собой переход из временной области в частотную область (и наоборот). Результат преобразования Фурье для периодического сигнала представляет собой эквивалент ряда Фурье, или спектр. На рис. 15 наглядно показаны первые шесть гармоник периодического сигнала прямоугольной формы.
Рис. 15. Графическое представление разложения в ряд Фурье для сигнала прямоугольной формы
Преобразование Фурье является интегралом функции с пределами интегрирования от минус до плюс бесконечности. Это можно записать в виде:
При отображении в S-плоскости переменная преобразования Фурье становится равной s = jω, а результатом будут только мнимые (комплексные) переменные.
Преобразование Лапласа является расширенным вариантом преобразования Фурье. Переменная преобразования Лапласа находится в комплексной плоскости, а интегрирование начинается с нуля, а не с минус бесконечности. При этом функция времени F(t) заменяется ее изображением, как функция от частоты F(s). Это означает, что данное преобразование может быть использовано для анализа ступенчатых или полубесконечных сигналов, таких как импульс или экспоненциальная последовательность с затуханием. Преобразование Лапласа можно записать в виде:
При переходе в S-плоскость переменная преобразования Фурье заменяется на s = σ + jω.
Используя преобразование Лапласа, можно математически смоделировать петлю обратной связи и генерацию нулей и полюсов на S-плоскости диаграммы. Вертикальная ось является мнимой, а горизонтальная ось — действительной. Чем выше или ниже они перемещаются по мнимой оси, тем быстрее возникают колебания. Чем дальше перемещение по отрицательной действительной оси, тем быстрее затухание, а чем далее перемещение по вещественной положительной оси, тем быстрее нарастание, что и поясняет рис. 16.
Рис. 16. График расположения нулей и полюсов в S-плоскости показывает соответствующие типичные временные диаграммы поведения системы
Нули всегда лежат на действительной оси. Комплексно сопряженные пары полюсов в левой половине S-плоскости объединяются так, чтобы сформировать отклик, который является затухающей синусоидальной функцией вида
где А и θ — это начальные условия, σ — скорость затухания, а ω — угловая частота в рад/с.
Пара полюсов, которая лежит на мнимой оси ±jω (без действительного компонента), генерирует колебания с постоянной амплитудой. Расстояние полюса от начала координат указывает на то, как происходит затухание отклика. Чем полюс ближе к началу координат, тем меньше скорость затухания. Если полюс находится на нуле, это означает, что перед нами система постоянного тока.
Если полюс находится в правой полуплоскости, система неустойчива (это соответствует понятию неустойчивости правой полуплоскости — RHP, описанному ранее).
Таблица 2 – КНИ для различных сочетаний выходной мощности на частотах 1 кГц и 10 кГц:
| Условия тестирования | КНИ (%) | ||
| F (кГц) | Pвых (Вт) | Rнагр (Ом) | |
| 1 | 7,5 | 8 | 0,00099 |
| 1 | 25 | 8 | 0,00198 |
| 1 | 15 | 4 | 0,00151 |
| 1 | 50 | 4 | 0,00229 |
| 10 | 7,5 | 8 | 0,00127 |
| 10 | 25 | 8 | 0,00216 |
| 10 | 15 | 4 | 0,00141 |
| 10 | 50 | 4 | 0,00290 |
Анализ показателей усилителя с помощью программы OrCAD 9.2 при условиях:
- номинальные значения напряжений источников питания: ±27 В и ±15 В;
- ток покоя VT16, VT17 = 130 мА;
- нагрузка усилителя 4 Ом;
- емкость С12 = 220 пФ;
- источники испытательных сигналов имеют нулевое сопротивление.
Компенсация наклона
Еще одной возможной причиной нестабильности петли обратной связи является субгармоническая бифуркация, или нестабильность, вызванная раздваиванием. Основная причина такой нестабильности — ШИМ-компаратор, который сравнивает уровень напряжения обратной связи с возрастающим пилообразным напряжением. Для того чтобы разобраться, обратимся к блок-схеме, приведенной на рис. 11.
Рис. 11. Блок-схема ШИМ-контроллера, работающего в режиме управления по напряжению (Voltage Mode Control)
Проблема здесь может возникнуть по той причине, что с каждым циклом переключения энергия в дросселе не исчезает полностью, так что ток, когда это не нужно, течет обратно в цепь обратной связи. Кроме того, это может быть просто переключением компаратора из-за наличия помех на его входе. Эффект аналогичен тому, как если бы ШИМ-модулятор формировал раздвоенный (это и есть бифуркация), или двойной, импульс.
Рис. 12. Временная диаграмма, иллюстрирующая субгармоническую нестабильность
Решение проблемы субгармонической неустойчивости называется компенсацией крутизны, или наклона (англ. Slope Compensation) (рис. 12). Такая компенсация заключается в том, чтобы добавить искусственный пилообразный сигнала (как правило, для этого используется спадающий ток дросселя, а иногда сигнал для компенсации берется непосредственно от напряжения на частотозадающем конденсаторе). Для того чтобы избежать ложных срабатываний или повторного запуска ШИМ-компаратора, это напряжение добавляется непосредственно к напряжению обратной связи (рис. 13).
Рис. 13. Компенсация наклона (пунктирная линия) и сигнал обратной связи (сплошная линия)
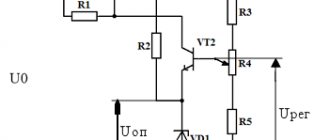
VceVT11 = VbeVT11 (1 + ( (R15 + R16) / R17) )
VceVT11 – напряжение между выводами коллектор-эмиттер; VbeVT11 – напряжение между выводами база-эмиттер.
Величина множителя напряжения Vbe устанавливается R15 приблизительно равной шести, то есть числу прямо смещенных эмиттерных переходов транзисторов, используемых в выходном буфере. Для снижения температурного дрейфа тока покоя VT16, VT17 – включение в их эмиттерные цепи резисторов R22, R23, R25-R28, R30, R31. Выбор номиналов указанных резисторов является компромиссом между стабильностью тока покоя мощных резисторов и КПД усилителя.
R9, R10 зашунтированы C8, C9, по переменному току включены параллельно и выполняют две функции одновременно: стабилизируют ток покоя VT5, VT6 и являются нижним плечом делителя напряжения цепи общей отрицательной ОС усилителя. Верхнее плечо делителя напряжения цепи ОООС образовано включенными параллельно по переменному току резисторами R12, R13. Коэффициент усиления УМЗЧ может быть рассчитан по формуле:
В результате анализа получены следующие данные:
- коэффициент усиления на частоте 1 кГц: 10,1;
- выходная мощность при уровне нелинейных искажений: 72 Вт/4 Ом;
- нижняя граница полосы пропускания на частоте 4,9 Гц: 3 дБ;
- входное сопротивление на частоте 1 кГц: 12,9 кОм;
- выходное сопротивление на частоте 1 кГц: 0,000433 Ом;
- проникновение на выход пульсаций с частотой 100 Гц порядка 1,3 мВ/В при пульсациях одного из источников и около 0,13 мВ/В при симметричных противофазных пульсациях двух источников.
Определение стабильности цифровой петли обратной связи с помощью билинейного преобразования
Если для формирования компенсации в петле обратной связи используется цифровой сигнальный процессор DSP (англ. DSP — Digital Signal Processor), стабильность такого цифрового контура может быть достигнута с помощью преобразования Лапласа для систем с дискретными сигналами.
В такой цифровой системе в качестве входного сигнала предусмотрен уже не непрерывный во времени сигнал, а дискретный в виде выборок с определенной частотой, называемой частотой дискретизации. Таким образом, значения переменных в s-плоскости должны быть преобразованы в дискретные значения Z-плоскости с выборкой по времени с помощью билинейного преобразования, известного как преобразование Тастина.
Результатом данного отображения является то, что устойчивая область в Z-плоскости превращается в окружность с радиусом, равным 1, в так называемую единичную окружность (рис. 17).
Рис. 17. Единичная окружность Z-плоскости
Удаленный правый край окружности (w = 0) представляет собой постоянный ток. Удаленный левый край окружности представляет собой частоту наложения спектров. Любые полюса, которые лежат вне этого круга, будут неустойчивыми. Полюса петли обратной связи теперь могут быть нанесены в Z-плоскости. Положения полюсов представляют нормированные отклики на частоту дискретизации, в отличие от сигналов непрерывных по времени, как это представлялось в S-плоскости.
Цифровая компенсация, во-первых, использует частоту дискретизации цифрового сигнального процессора, которая намного выше, чем системная частота перехода, так что любые расчеты являются точными. Для того чтобы найти значения параметров компенсации, здесь возможны два общих подхода. Первый — переработка в цифровую форму параметров компенсации на основе первичной разработки аналоговой системы управления, а второй — прямая разработка уже непосредственно цифрового управления. При переносе аналогового управления в цифровой вариант первоначально устанавливается линейная модель импульсного преобразователя. Причем компенсация петли обратной связи моделируется обычно в S-плоскости. А потом, для того чтобы завершить проектирование уже цифровой компенсации, результаты полученной аналоговой компенсации отображаются в z-плоскость. При непосредственном подходе к проектированию цифрового управления дискретная модель импульсного преобразователя является полностью моделируемой с использованием цифрового управления, а решение в части компенсации рассчитывается непосредственно в Z-плоскости. Это требует применения точных моделей всех аналоговых элементов, а моделирование осуществляется с помощью таких программ, как Spice или Matlab.
Результат обоих методов один и тот же — рассчитанная матрица значений сохраняется как таблица преобразования. DSP или микроконтроллер будут получать оцифрованный входной сигнал, вводить его для вычисления в матрицу, а на выходе иметь полученное значение либо как аналоговый сигнал управления, либо, что используется чаще всего, как скорректированный выходной сигнал управления непосредственно самого ШИМ-драйвера. В последнем случае схемы компаратора и цепи формирования ШИМ также будут синтезированы в цифровом виде. Это исключает ошибки контура аналогового управления, связанные с компенсацией наклона, и нестабильность RHP. Если требуется обрабатывать иной режим работы компенсации обратной связи на отклик, то цифровой контроллер может плавно переключаться между таблицами преобразования без сброса выхода преобразователя. Это уникальная способность, не свойственная аналоговым контроллерам. Таким образом, количество компромиссов, которым нужно следовать при выборе необходимой характеристики компенсации, значительно снижается.
Именно это отсутствие компромиссов и способность буквально мгновенно переключаться между быстрой переходной характеристикой или стабильным выходом и делает цифровой контур обратной связи таким привлекательным. Поскольку стоимость микроконтроллеров продолжает снижаться, то все больше и больше DC/DC-преобразователей будут мигрировать в сторону контроллеров с полностью цифровыми или гибридными петлями обратной связи.
Определение стабильности петли обратной связи экспериментальным путем
Стабильность поведения контура обратной связи можно определить экспериментально с помощью прибора для построения диаграммы Боде (получения логарифмической амплитудно-фазовой частотной характеристики), которая является представлением частотного отклика линейной стационарной системы в логарифмическом масштабе. Для того чтобы ввести сигнал возмущения в контур управления, можно использовать внешний генератор синусоидального сигнала со звуковым трансформатором, через который и подается возмущающий сигнал (рис. 14). Частота этого внешнего синусоидального сигнала линейно возрастает вплоть до уровня возмущения на выходе, равного по уровню возмущающему сигналу. Усиление в данном случае равно 1, и, таким образом, частота возмущающего сигнала должна быть равна частоте перехода fc контура обратной связи. Разность фаз между возмущающим сигналом и выходным сигналом и является запасом по фазе. При дальнейшем увеличении частоты до тех пор, пока разность фаз не достигнет –180°, может быть найден запас по усилению.
Рис. 14. Схема для экспериментального построения диаграммы Боде
К = 1 + Reqv1 / Reqv2
Reqv1 – эквивалентное сопротивление параллельно включенных резисторов R12 и R13; Reqv1 – эквивалентное сопротивление параллельно включенных резисторов R9 и R10.
Динамические характеристики усилителя определяются частотными свойствами и режимами работы транзисторов, а также сопротивлениями R12, R13 цепи ОООС и ёмкостью С12 частотной коррекции. Вариации коэффициента усиления УМЗЧ синхронным изменением R9, R10 ширина полосы изменяется незначительно. Этим усилитель с токовой ОС принципиально отличается от традиционных УМЗЧ, у которых произведение коэффициента усиления на ширину полосы пропускания является постоянной величиной.