Механические характеристики асинхронных двигателей

Асинхронный двигатель преобразовывает электрическую энергию в механическую. Механическая характеристика асинхронного двигателя, электромеханическая и другие содержат информацию, без которой невозможна его правильная эксплуатация.

Эта конструкция достаточно широко применяется в различных сферах человеческой жизнедеятельности. Без них немыслима работа станков, транспортеров, подъемно-транспортных машин. Двигатели, обладающие небольшой мощностью, широко используются в автоматике.

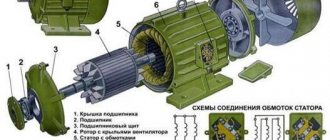
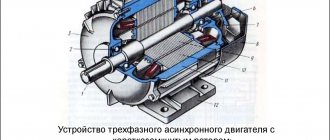
Устройство асинхронной машины

Схематичное устройство асинхронной машины

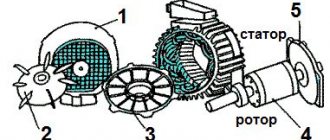
Классическая асинхронная машина состоит из 2 основных частей: ротора (подвижной) и статора (неподвижной). Три отдельные фазы составляют обмотку статора. С1, С2 и С3 — обозначения начала фаз. С3, С4 и С5 — соответственно концы фаз. Все они подсоединены к клеммному разъему по схеме звезда или треугольник, что показано на рисунках а, б, в. Схему выбирают учитывая паспортные данные двигателя и сетевое напряжение.

Статор создает внутри электродвигателя магнитное поле, которое постоянно вращается.

Ротор различают короткозамкнутый и фазный.

В короткозамкнутом скорость вращения не регулируется. Конструкция с ним проще и дешевле. Однако пусковой момент у него слишком мал по сравнению с машинами, у которых фазный ротор. Здесь скорость вращения регулируется за счет возможности ввода дополнительного сопротивления.

Принцип работы асинхронной машины

Подавая напряжение на обмотку статора, по каждой фазе можно наблюдать изменяющиеся магнитные потоки, которые по отношению друг к другу смещены на 120 градусов. Общий результирующий поток получается вращающимся и создает ЭДС внутри проводников ротора.

Там появляется ток, который во взаимодействии с результирующим потоком создает пусковой момент. Это приводит к вращению ротора.

Возникает скольжение S, т. е. разность между частотой вращения самого ротора n2 и частотой магнитного поля статора n1. Первоначально оно равно 1. Впоследствии частота возрастает, разность n1 – n2 уменьшается. Это ведет к уменьшению вращающего момента.

На холостом ходу скольжение минимально. Оно достигает критического значения Sкр, когда увеличивается статический момент. Превышение Sкр ведет к нестабильной работе машины.

Рабочие характеристики асинхронного двигателя

Рабочие характеристики асинхронного двигателя

— зависимости потребляемого тока I1 и мощности Р1, КПД, cos φ и скольжения s от полезной механической мощности P2. Эти характеристики определяются при постоянном напряжении U1 и частоте f1 сети.

Рабочие характеристики асинхронного двигателя

могут быть получены экспериментально (опытным путем) и рассчитаны с помощью схемы замещения.

Ниже приводится расчет рабочих характеристик асинхронного двигателя

по схеме замещения.

По обмотке статора асинхронной машины протекает многофазная система токов, обычно трехфазная, которая создает в воздушном зазоре машины вращающееся магнитное поле (магнитный поток Ф).

Вращающееся магнитное поле в свою очередь индуктирует (наводит) в проводниках обмотки ротора ЭДС, под действием которой в замкнутой накоротко обмотке ротора протекает ток I2. Этот ток, взаимодействуя с магнитным потоком Ф, создает механическую силу, стремящуюся привести ротор во вращение в сторону вращения магнитного поля.

Определим, с какой частотой вращения магнитное поле машины пересекает проводники ротора. Эта частота равна, об/мин:

(9)

Определим частоту ЭДС f2, которая наводится магнитным полем асинхронной машины в проводниках ротора, Гц:

f2=р n2/60. (10)

Если учесть, что n2=n1s [см. формулу (9)], то можно записать

(11)

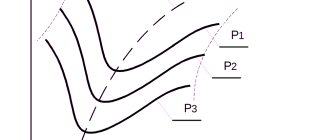
Из формулы (11) видно, что если ротор машины неподвижен (n=0, s=l), то частота ЭДС, наводимой в роторе, равна частоте сети. По мере увеличения частоты вращения ротора ЭДС понижается и при синхронной частоте будет равна нулю. На рис. 13 показаны изменения скольжения, частоты и ЭДС в роторе в зависимости от частоты вращения ротора.

Рис. 13. Зависимость скольжения s, частоты f2 и ЭДС, наводимой в роторе, E2 от частоты вращения асинхронного двигателя n

Из закона электромагнитной индукции следует, что при гармоническом изменении магнитного поля наводимая в обмотке ЭДС равна:

E=4,44fwkобФmax, (12)

где f — электрическая частота, Гц; w — число последовательно соединенных витков фазы; kоб — обмоточный коэффициент; Фmax — максимальное значение рабочего потока, сцепленного с обмоткой, Вб.

Знание частоты f2 в роторе дает возможность определить ЭДС ротора Е2 при произвольной частоте вращения (скольжении), В, в виде

E2=4,44f2w2kоб2Фmax, (13)

где w2 — число последовательно соединенных витков обмотки ротора; kоб2 — обмоточный коэффициент ротора.

Подстановка f2 из формулы (11) дает, В,

E2s=4,44f s w2kоб2Фmax=sE2, ( 14)

где Е2 — ЭДС, наводимая в неподвижной обмотке ротора потоком Фmax, В.

Осветим теперь важный для анализа работы асинхронных двигателей вопрос о зависимости вращающегося магнитного потока двигателя от режима работы машины. Для этого, чтобы представить себе эту зависимость, определим вначале, какую ЭДС Е1 наводит этот поток в каждой фазе обмотки статора, В:

E1=4,44fw1kоб1Фmax, (15)

где w1 — число витков одной фазы статора; kоб1 —обмоточный коэффициент обмотки статора.

Напряжение U1, приложенное к статору, уравновешивается ЭДС E1 и падением напряжения I1z1 на внутреннем сопротивлении z1=r1+jx1 обмотки статора (х1— индуктивное сопротивление обмотки, определяемое потоком рассеяния) . При изменении нагрузки двигателя от нуля (холостой ход) до номинальной падение напряжения составляет 5—10 % приложенного. Таким образом, с достаточной для качественного анализа точностью можно полагать, что напряжение U1 полностью компенсируется ЭДС Е1 т. е. .

U1≈E1 (16)

Учитывая формулу (15), нетрудно заключить, что ЭДС и вращающийся магнитный поток двигателя зависят от приложенного к двигателю напряжения. При постоянном напряжении поток Фmах остается приблизительно постоянным независимо от изменения нагрузки двигателя.

Рассмотрим вначале явления, происходящие в машине с заторможенным ротором и замкнутой накоротко обмоткой ротора. Асинхронный двигатель

в этом режиме подобен трансформатору с короткозамкнутой вторичной обмоткой. Отличие состоит в том, что вторичная магнитная цепь отделена от первичной воздушным зазором, первичная обмотка (статора) и вторичная обмотка (ротора) равномерно распределены по окружности, а магнитное поле вращающееся.

Как видно из формулы (14) и рис. 13, ЭДС, наводимая в обмотке ротора, когда он неподвижен, является максимальной. В силу этого и ток, проходящий по обмоткам статора и ротора, также будет наибольшим. Этот режим называется режимом короткого замыкания (КЗ). Ток статора в этом режиме называется током короткого замыкания и превышает его номинальный ток в 4—7 раз. Асинхронный двигатель

в таких условиях нельзя длительно оставлять под полным напряжением из-за перегрева обмоток, который может привести к аварии.

Для определения тока короткого замыкания двигателя делают опыт КЗ. Этот опыт заключается в том, что к двигателю с заторможенным (неподвижным) ротором подводят пониженное напряжение, регулируя которое, устанавливают номинальный ток. Напряжение, подводимое к двигателю в опыте КЗ, оказывается малым (15— 20%) по сравнению с номинальным. На базе этого опыта можно в безопасных для двигателя условиях определить величину тока короткого замыкания /к при номинальном напряжении, А:

(17)

где Uном — номинальное напряжение, В; Uк — напряжение в опыте КЗ при номинальном токе, В; Iном — номинальный ток, А.

Замеряя в этом опыте по ваттметру мощность короткого замыкания Рк, подводимую к одной фазе двигателя, находят также коэффициент мощности в режиме КЗ

(18)

и эквивалентное активное сопротивление статора и ротора двигателя гк в режиме КЗ на одну фазу, Ом,

rк=Pк/Iном2 (19)

Это эквивалентное активное сопротивление равно сумме активного сопротивления статора и приведенного активного сопротивления ротора. Понятие о приведенном активном и реактивном сопротивлении ротора будет дано ниже.

Определив угол φк по значению cosφк из формулы (18), легко найти и эквивалентное реактивное сопротивление двигателя в режиме короткого замыкания, Ом:

хк=rкctgφк (20)

Индуктивное сопротивление хк равно сумме индуктивного сопротивления статора и приведенного индуктивного сопротивления ротора.

Поскольку частота вращения ротора двигателя в этом режиме равна нулю, его механическая мощность также равна нулю. Потери в стали во время опыта короткого замыкания очень малы, так как мал вращающийся магнитный поток. Поэтому мощность Рк, которая подводится к машине, почти вся идет на нагрев проводников обмоток статора и ротора. То же самое можно сказать о режиме КЗ при полном напряжении.

Теперь представим себе, что обмотка ротора разомкнута, а обмотка статора включена в сеть. Ток по роторной обмотке при этом не проходит и асинхронный двигатель

подобен трансформатору, но уже в режиме холостого хода (XX). Так как ток в проводниках ротора отсутствует, то механическая сила не возникает и ротор остается неподвижным.

По обмотке статора при этом проходит ток холостого хода I0, который создает магнитодвижущую силу (МДС), необходимую для создания магнитного потока Фmax. Поскольку в магнитной цепи асинхронного двигателя имеется зазор, то для создания магнитного потока требуется относительно больший ток, чем в трансформаторе. В двигателях большой и средней мощности ток XX составляет 25—35, а в двигателях малой мощности — 35—60% номинального тока.

Наводимая в неподвижном роторе ЭДС может быть определена по формуле (14), если учесть, что скольжение в этом режиме равно 1. Отношение ЭДС в обмотке статора к ЭДС в обмотке ротора называется коэффициентом трансформации ЭДС и может быть определено по формуле

(21)

Мощность, потребляемая двигателем в режиме XX при неподвижном роторе, расходуется на потери в проводниках статора двигателя, потери на перемагничивание и вихревые токи в стали статора и в стали ротора.

Важно заметить, что режим XX при неподвижном роторе очень близок к режиму, который возникает, когда асинхронный двигатель

не выполняет полезной работы и вращается на холостом ходу. В этом случае частота вращения ротора двигателя почти равна синхронной, а скольжение примерно равно нулю [см. формулы (4), (9) и рис. 13]. Электродвижущая сила в роторе будет близкой к нулю, и, следовательно, подобно режиму XX при неподвижном роторе практически равен нулю ток в роторе. При холостом ходе вращающегося двигателя ток в обмотке статора, как и в случае холостого хода неподвижного двигателя, определяется в основном МДС, необходимой для создания магнитного потока Фmax.

При вращении ротора в двигателе появляются потери, которых нет в случае неподвижного ротора; это механические потери на трение и вентиляционные. Однако когда частота вращения ротора примерно равна синхронной, исчезают потери в стали ротора двигателя, поскольку магнитное поле теперь очень медленно перемещается относительно ротора и его сталь почти не перемагничивается. Таким образом, потери и, следовательно, мощность в двух режимах холостого хода оказываются близкими.

Асинхронная машина в режиме холостого хода может быть представлена схемой замещения, показанной на рис. 14. Для определения параметров и характеристик двигателя помимо опыта КЗ выполняют опыт XX, во время которого замеряют ток обмотки статора I0 (А) и потребляемую мощность Р0 (Вт). Это позволяет определить сопротивления в схеме замещения двигателя на холостом ходу, а также коэффициент мощности XX:

cosφ0=P0/(UI0). (22)

Рис. 14. Схема замещения первичной цепи (статора) асинхронного двигателя, работающего в режиме холостого хода

Перейдем теперь к рассмотрению общего случая режима нагрузки, когда ротор вращается с частотой, меньшей частоты XX. Определим, какой ток будет проходить по обмотке ротора во всем диапазоне рабочих режимов. Наводимая вращающимся магнитным потоком ЭДС в обмотке ротора зависит при постоянном напряжении только от скольжения и может быть найдена по (14). Ток ротора будет, очевидно, зависеть от ЭДС, наводимой в роторе, и сопротивления обмотки ротора, при этом полное сопротивление цепи в случае переменного тока определяется не только активным сопротивлением проводников обмотки, но и ее индуктивным сопротивлением. Индуктивное сопротивление обмотки ротора изменяется так же, как и ЭДС ротора E2s, Ом:

x2s=2πf2L2=s2πf1L2 =sx2, (23)

где L2 — индуктивность обмотки ротора, Гн; х2— индуктивное сопротивление рассеяния обмотки неподвижного ротора при s=l, Ом.

Теперь, используя закон Ома для цепей переменного тока, найдем ток ротора, А:

(24)

Учитывая (14) и (23), формулу (24) можно записать иначе:

(25)

Таким образом, можно видеть, что при скольжении, равном нулю или близком к нему (это соответствует синхронной или близкой к синхронной частоте вращения ротора), ток ротора равен нулю или очень мал. Это совпадает с тем, что было сказано выше относительно режима XX при вращающемся роторе. По мере уменьшения частоты вращения двигателя, т. е. при увеличении скольжения, ток возрастает за счет увеличения ЭДС ротора, однако рост тока ограничивается увеличением индуктивного сопротивления ротора.

Если разделить числитель и знаменатель выражения (25) для тока ротора I2 на s, то получим следующую формулу:

(26)

Из этого следует, что если мы примем, что ротор неподвижен, а его активное сопротивление меняется обратно пропорционально скольжению, то по его обмотке будет проходить точно такой же ток, как и при вращающемся роторе. Удобство такого преобразования состоит в том, что оно позволяет вместо вращающегося ротора (вращающаяся вторичная электрическая цепь) рассматривать неподвижный ротор (неподвижная вторичная цепь).

Однако изучение процессов, происходящих в асинхронной машине, и расчет ее характеристик можно сделать более удобными, если заменить реальную обмотку ротора эквивалентной с числом витков в фазе и числом фаз, равным им у первичной обмотки (обмотки статора), т. е. вместо обмотки ротора с числом фаз m2, числом витков в фазе w2 и обмоточным коэффициентом kоб2 будем полагать, что обмотка ротора имеет число фаз ти число витков в фазе w1 и обмоточный коэффициент kоб1. Эта замена называется приведением обмотки ротора к обмотке статора. Нетрудно видеть, что магнитный поток Ф в этом случае будет наводить в эквивалентной (приведенной) обмотке ротора ЭДС, равную ЭДС обмотки статора E2’=E1 (штрихом будем обозначать приведенные величины).

Замена обмотки ротора не должна привести к изменению потребляемой мощности, потерь, магнитодвижущей силы и фазы тока обмотки. Из этого условия определяются приведенные величины тока, активного и индуктивного сопротивлений обмотки ротора .

В соответствии с (13) имеем, В

(27)

Из формул (27) вытекает отношение между ЭДС приведенной и реальной обмоток заторможенного ротора, которое называется коэффициентом трансформации ЭДС или напряжений. Он равен:

(28)

Из условия неизменности магнитодвижущих сил F2′ =F2 следует, что

откуда вытекает отношение между токами, которое называется коэффициентом трансформации токов. Он равен:

(29)

Из условия неизменности потерь в обмотке ротора при приведении следует, что

откуда

(30)

или r2’=krr2,

где kr=kIkU — коэффициент приведения сопротивлений.

Из условия неизменности фазы тока обмотки ротора следует

(31)

Процесс приведения цепи ротора показан на рис. 15. От схемы замещения обмотки вращающегося ротора (рис. 15,а) переходим к схеме замещения неподвижного ротора (рис. 15,б), а затем приводим обмотку ротора к обмотке статора (рис. 15, в).

Рис. 15. Схемы замещения: а — обмотки вращающегося ротора; б — неподвижного ротора; в — обмотки ротора, приведенной к обмотке статора

Поскольку теперь ЭДС Е1 первичной обмотки равна ЭДС Е2′ вторичной обмотки, мы можем соединить электрически соответствующие точки схемы замещения обмотки статора и ротора. В результате получим схему замещения асинхронного двигателя, показанную на рис. 16. Здесь активное сопротивление rm отражает наличие потерь в стали двигателя. Для двигателей средней и большой мощности удобнее пользоваться упрощенной схемой замещения, приведенной на рис. 17.

Рис. 16. Т-образная схема замещения асинхронного двигателя

Рис. 17. Упрощенная Г-образная схема замещения асинхронного двигателя

Используя последнюю схему, легко найти токи и ЭДС в обмотках, подводимую и полезную мощность, а также мощность потерь при любой частоте вращения двигателя. Для этого следует лишь найти скольжение, соответствующее заданной частоте n, по формуле (4) и вычислить сопротивление r2’/s в схеме по рис. 17. После этого нетрудно найти ток намагничивания I0 и приведенный ток I2′ в роторной цепи, А:

(32)

Это дает возможность вычислить электрические потери в обмотке статора трехфазного двигателя (m1=3), Вт:

(33)

Электрические потери в обмотке ротора (Вт) можно найти, предварительно рассчитав по (30) приведенное сопротивление ротора r2′ (Ом):

(34)

Суммарная активная мощность, передаваемая со статора на ротор, как видно из схемы (рис. 17), будет равна, Вт:

(35)

Эта мощность передается на ротор электромагнитным путем и поэтому называется электромагнитной мощностью.

Если из электромагнитной мощности вычесть мощность электрических потерь в обмотке ротора, то получим полную механическую мощность двигателя, Вт:

(36)

Полная механическая мощность расходуется на вращение приводного механизма (полезная механическая мощность) и на покрытие механических Рмх.п и добавочных Рд.п потерь самого двигателя. Поэтому полезная механическая мощность Р2 будет равна, Вт:

(37)

Коэффициент полезного действия двигателя по определению равен отношению отдаваемой (полезной механической) мощности к потребляемой (активной электрической) мощности. Разность между этими мощностями составляют потери в двигателе, равные, Вт:

где Pм.п=m1I02rm — магнитные потери или потери в стали. Таким образом, КПД двигателя равен:

(38)

Использование первого или второго выражения для КПД определяется тем, какая из мощностей — P1 или Р2— известна. На практике наиболее часто применяется первое выражение (38).

Используя схему замещения, можно определить также ток, потребляемый двигателем из сети, т. е. ток статора, который равен сумме двух токов. Первый из них — это ток XX, который протекает по цепи 1 (рис. 17) и не изменяется при изменении частоты вращения ротора, второй — ток ротора I2′, который определяется по (32). Складывая геометрически эти два тока, можно получить ток статорной обмотки. Такое геометрическое сложение показано на рис. 18. Углы φ2′, φ0, необходимые для построения, можно найти с помощью схемы замещения (см. рис. 17):

Таким образом, знание параметров схемы замещения (r1, x1, r2′, х2′, rm, хm) и приложенного напряжения U1 (напряжение сети) позволяет с помощью приведенных выше формул определить полезную мощность, токи, потери, КПД, коэффициент мощности двигателя при различных скольжениях (частоте вращения).

Рис. 18. Диаграмма токов асинхронного двигателя

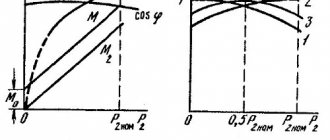
Зависимости потребляемого тока I1 и мощности Р1, КПД, cosφ и скольжения s от полезной механической мощности P2 носят название рабочих характеристик двигателя. Эти характеристики определяются при постоянном напряжении U1 и частоте f1 сети. Пример рабочих характеристик приведен на рис. 19.

Рис. 19. Рабочие характеристики асинхронного двигателя

Рассмотрим рабочие характеристики асинхронного двигателя

. При холостом ходе (полезная мощность Р2—0) скольжение s также равно нулю (частота вращения ротора n практически равна синхронной), сопротивление r2/’s равно бесконечности (см. рис. 17) и ток I2’==0. По обмотке статора протекает ток холостого хода I0. Коэффициент полезного действия η равен нулю, так как равна нулю полезная мощность Р2, а коэффициент мощности равен коэффициенту мощности для тока холостого хода (cosφ1=cosφ0).

При увеличении нагрузки частота вращения ротора уменьшается и увеличивается скольжение s. За счет увеличения s уменьшается сопротивление цепи 2 (см. рис. 17) и увеличивается ток ротора, а следовательно, и ток статоpa. Поскольку увеличивается полезная мощность, растет, КПД двигателя, а также коэффициент мощности.

Обычно номинальная мощность на валу двигателя достигается уже при небольшом понижении частоты вращения ротора и вся область рабочих режимов находится в диапазоне скольжений от 0 до 2—5%.

Поэтому скоростная характеристика n=f(P2) у асинхронного двигателя имеет небольшой наклон к оси абсцисс. Характеристики такого вида принято называть жесткими. Соответственно характеристика s=f(P2) имеет слабый подъем при возрастании нагрузки. В асинхронном двигателе частота вращения ротора меньше частоты вращения поля, за счет чего обеспечивается наведение ЭДС, а также создание тока 1% в обмотке ротора и вращающего электромагнитного момента, под действием которого ротор приходит во вращение.

Характеристика cosφ=f(P2) лежит в области значений, меньших 1, так как асинхронный двигатель

всегда потребляет ток I0, почти не зависящий от нагрузки в диапазоне мощностей от Р0 до Р2≈Рном. При XX обычно φ0<0,2, т. е. он содержит большую реактивную составляющую. При увеличении нагрузки cosφ быстро возрастает и достигает максимального значения при мощности Р2≈Р2ном. При увеличении нагрузки выше номинальной cosφ несколько снижается.

Коэффициент полезного действия достигает своего максимального значения при Р2≈ (0,6÷0,8)Р2ном и снижается при дальнейшем росте нагрузки. Поскольку двигатель обычно работает при переменной нагрузке, изменяющейся в пределах (0,6—1)Р2ном, то КПД в этом диапазоне изменения нагрузки должен быть достаточно высок.

Механическая характеристика

Как основная, помогает проводить детальный анализ работы электродвигателя. Она выражает непосредственную зависимость частоты вращения самого ротора от электромагнитного момента n=f (M).

Точка 2 — номинальный режим работы. Точка 3 — частота вращения достигла критического значения. Пусковой момент Мпуск — точка 4.

Наши читатели рекомендуют! Для экономии на платежах за электроэнергию наши читатели советуют ‘Экономитель энергии Electricity Saving Box’. Ежемесячные платежи станут на 30-50% меньше, чем были до использования экономителя. Он убирает реактивную составляющую из сети, в результате чего снижается нагрузка и, как следствие, ток потребления. Электроприборы потребляют меньше электроэнергии, снижаются затраты на ее оплату.

Существуют технические способы расчетов и построения механической характеристики с учетом данных паспорта.

В первоначальной точке 1 n0=60f/p (p – количество пар полюсов). Поскольку nн и Mн непосредственно координаты точки 2, расчет номинального момента производится по формуле Mн=9,55*Рн/ nн, где Рн — номинальная мощность. Значение nн указано в паспорте двигателя. В точке 3 Mкр=Mнλ. Пусковой момент в точке 4 Mпуск=Mн*λпуск (значения λ, λпуск — из паспорта).

Механическая характеристика, построенная таким образом, называется естественной. Изменяя другие параметры можно получить искусственную механическую характеристику.

Полученные результаты дают возможность проанализировать и согласовать механические свойства самого двигателя и рабочего механизма.

Электромеханическая и механическая характеристика АД.

Схема включения и статические характеристики асинхронного двигателя.

Асинхронные двигатели широко применяются в промышленности благодаря простоте их конструкции, надежности и низкой стоимости.

Трехфазный АД имеет обмотку статора, подключаемую к трехфазной сети переменного тока с напряжением U

и частотой
f
, и обмотку ротора, которая может быть выполнена в двух вариантах. АД с фазным ротором (выполнение обычной трехфазной обмотки из проводников с выводами на три контактных кольца). АД с короткозамкнутым ротором – выполнение обмотки заливкой алюминия в пазы ротора (рис 5.1). Однофазная схема замещения (рис. 5.1)

Рис Схема включения АД с фазным (а), короткозамкнутым ротором (б), Г-образная однофазная схема замещения АД

U1

– действующее значение напряжения, приложенного к одной фазе обмотки статора, частотой
f1
;

Рис Фазное и линейное напряжения

Iμ, I1, I’2 – фазные токи соответственно намагничивания, обмотки статора и ротора (приведенный к числу витков обмотки статора);

R1 – суммарное активное сопротивление фазы статора;

R’2= R’р + R’2д – суммарное активное сопротивление фазы ротора, приведенное к числу витков обмотки статора. Включает в себя R’р, – собственное сопротивление обмотки ротора (приведенное); R’2д – добавочное активное сопротивление (приведенное).

x1, x’2 – индуктивные сопротивления рассеяния соответственно фазы обмотки статора, обмотки ротора (приведенное к числу витков обмотки статора);

Rμ – активное сопротивление, учитывающее потери в стали магнитной системы при перемагничивании;

xμ – индуктивное сопротивления контура намагничивания.

При включении статора в сеть трехфазного тока его обмотки создают магнитное поле Ф

, которое вращается со скоростью
n1
. Силовые линии этого поля пересекают обмотку ротора и индуктируют в ней ЭДС
E2
.

Величина ЭДС пропорциональна разности скоростей поля статора и ротора:

E2~( n1- n)Ф

(#)

По обмотке ротора под действием ЭДС E2

потекут токи, создающие магнитное поле ротора. Магнитное поле ротора взаимодействует с вращающимся полем статора, возникает вращающийся момент. Начав движение, ротор будет «догонять» поле статора. Но у асинхронного двигателя всегда
n< n1
. Иначе при равенстве исчезает ЭДС
E2
, токи, и магнитное поле ротора, и начинается торможение.

Отставание ротора от магнитного поля статора называется скольжением:

= (1)

Отметим, что в схеме замещения зависимость R’2

от скольжения
s
не соответствует физической сущности электромагнитных процессов. В действительности от скольжения зависит индуктивное сопротивление ротора X’2. Так, X’2=ω2L2=2πf2L2 (*). В то же время известно, что частота
f2
ЭДС
Е2
в обмотке ротора зависит от скольжения
f2 = f1 s
. Выполненное же преобразование (деление на s) позволило составить схему замещения.

Электромеханическая и механическая характеристика АД.

В отличие от ДПТ электромеханическая характеристика АД представляется в виде зависимости тока ротора от скольжения I’2= f( s)

, а не от скорости ω. Уравнение электромеханической характеристики следует из схемы замещения:

(2)

В то же время скольжение однозначно определяет величину скорости:

Из (1) (3)

Поэтому при построении характеристик I’2(s) отражается и зависимость I’2

(ω).

Рис Электромеханическая характеристика

На графике ток I1 больше тока I’2 в соответствии со схемой замещения на величину тока холостого хода Iμ (первый закон Кирхгофа).

Рассмотрим характерные точки электромеханической характеристики:

1) Идеальному холостому ходу соответствует скорость вращения ротора ω= ω0

,

скольжение s=0

(ротор и поле статора вращаются синхронно), ток ротора
I’2=0
, статора
I1= Iμ
. Асинхронный двигатель самостоятельно обеспечить этот режим не может. Для создания режима необходимо приводить во вращение с частотой
ω=ω0
другим двигателем. На схеме замещения этому режиму соответствует разрыв цепи ротора (
I’2
).

2) Короткому замыканию (режим пуска) соответствует режим, когда ω=0

, скольжение
s=1
, ток ротора
I’2= I’2п
, статора
I1= I1п
. Ток
I1п
называется пусковым током, достигает 5-7 кратного значения от номинального тока.

, получили приняв s=1;

3) токи статора и ротора I1, I­­­’2

достигают своего максимального значения при минимуме знаменателя выражения (2), когда =>

Этот режим наступает при скоростях выше синхронной ω0

, т.е. в генераторном режиме.

4) При высоких скоростях ω=±∞

, s=
±∞,
значение тока ротора асимптотически приближается к значению

;

Получим выражение для механической характеристики. Потери мощности в цепи ротора (потери скольжения), представляют собой разность электромагнитной и полезной механической мощности:

Потери мощности в роторе, выраженные через электрические величины:

=> , подставив в выражение ток (2) получим

Рис. Механическая характеристика АД

Для определения критического скольжения sк

и момента
Мк
исследуем полученную зависимость M(s) на экстремум обнаружим две точки.

(5) (+ в двигательном, — в генераторном)

Разделив (4) на (5) и выполнив преобразования, получим более удобную форму:

, где — формула Клосса

Для машин средней и большой мощности можно пренебречь активным сопротивлением статора, тогда a=0 и

(6)

Кроме того, в области малых скольжений можно пренебречь s/sк, тогда

(7)

Из (6), обозначив как можно получить выражения для нахождения sк

:

Формула может быть использована для определения sк

по каталожным данным.

Проанализируем особенности механической характеристики АД. Она носит нелинейный характер и состоит из двух частей. Первая – рабочая часть – в пределах скольжения от 0 до sкд. Эта часть характеристики близка к линейной и имеет отрицательную жесткость. Здесь момент, развиваемый двигателем, примерно пропорционален токам статора и ротора. Можно использовать выражение (7).

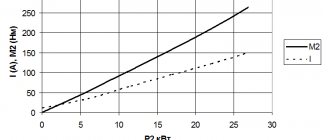
Вторая часть механической характеристики АД при s>sкд – криволинейная, с положительным значением жесткости. Несмотря на то, что ток двигателя по мере роста скольжения увеличивается (рис 5.3), момент, напротив уменьшается.

Из-за нелинейности механической характеристики существует несоответствие между пусковым током (5-7 кратный) и пусковым моментом (0,4-0,5 номинального). Тяжелый пуск.

Рассмотрим процесс пуска.

Пуск начинается с s=1, в начале пуска скольжение велико. Индуктивное сопротивление обмотки ротора X’2=ω2L2=2πf2L2=2 πsf1L2 велико и существенно превосходит R’2. X2′>>R2′.

ЭДС при этом велика, поскольку ~Ф(n1-n)

Поэтому ток I’2 тоже велик, но его активная составляющая мала (потому что cosφ низкий). Поэтому и момент, развиваемый двигателем мал.

2) При разгоне двигателя скольжение уменьшается, ЭДС ротора снижается, частота тока f2 и X2′ ротора пропорционально уменьшаются.

Соответственно уменьшается полный ток ротора. Активное сопротивление становится соизмеримым с индуктивным, а затем и становится больше. Вследствие повышения cosφ, активная составляющая тока растет, возрастает и момент двигателя.

Т.е. своеобразие механической характеристики АД определяется зависимостью индуктивного сопротивления ротора от скольжения.