У этого термина существуют и другие значения, см. Мост (электротехника).
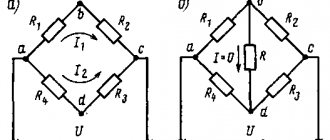
Принципиальная схема моста Уитстона. Обозначения:
- R 1 {\displaystyle R_{1}} , R 2 {\displaystyle R_{2}} , R 3 {\displaystyle R_{3}} , R x {\displaystyle R_{x}} — «плечи» моста;
- AC — диагональ питания;
- BD — измерительная диагональ;
- R x {\displaystyle R_{x}} — элемент, сопротивление () которого требуется измерить;
- R 1 {\displaystyle R_{1}} , R 2 {\displaystyle R_{2}} и R 3 {\displaystyle R_{3}} — элементы, сопротивления () которых известны;
- R 2 {\displaystyle R_{2}} — элемент, сопротивление которого может регулироваться (например, реостат);
- V G {\displaystyle V_{G}} — гальванометр ();
- R G {\displaystyle R_{G}} (не показано) — сопротивление гальванометра ().
Измери́тельный мост
(
мост Уи́тстона
,
мо́стик Ви́тстона
[1], англ. Wheatstone bridge) — электрическая схема или устройство для измерения электрического сопротивления. Предложен в 1833 году Самуэлем Хантером Кристи (англ. Samuel Hunter Christie) и в 1843 году усовершенствован Чарльзом Уитстоном[2]. Мост Уитстона относится к одинарным мостам в отличие от двойных мостов Томсона. Мост Уитстона — электрическое устройство, механическим аналогом которого являются аптекарские рычажные весы.
Содержание
- 1 Измерение сопротивлений с помощью моста Уитстона 1.1 Точность
- 1.2 Недостатки
- 7.1 Принцип работы тензометрических измерителей
Вопросы о ММВ
Поля отмеченные * обязательны для заполнения.
Мы предлагаем электротехническое оборудование:
| Название | Цена (без НДС) |
| МК4700 | — |
| МКИ-200 | — |
| МКИ-600 | — |
| ММВ — Мост постоянного тока |
Электроизмерительные приборы / Мосты, потенциометры
Мост Уинстона переносной линейный ММВ предназначен для технических измерений сопротивления постоянному току.
| Гарантия: 12 месяцев |
Измерение сопротивлений с помощью моста Уитстона
Принцип измерения сопротивления основан на уравнивании потенциала средних выводов двух ветвей (см. рисунок).
- В одну из ветвей включён двухполюсник (резистор), сопротивление которого требуется измерить ( R x {\displaystyle R_{x}} ).
Другая ветвь содержит элемент, сопротивление которого может регулироваться ( R 2 {\displaystyle R_{2}} ; например, реостат).
Между ветвями (точками B и D; см. рисунок) находится индикатор. В качестве индикатора могут применяться:
- гальванометр;
- нуль-индикатор — прибор, отклонение стрелки которого показывает наличие тока в цепи и его направление, но не величину. На шкале такого прибора отмечено только одно число — ноль;
- вольтметр ( R G {\displaystyle R_{G}} принимают равным бесконечности: R G = ∞ {\displaystyle R_{G}=\infty } );
- амперметр ( R G {\displaystyle R_{G}} принимают равным нулю: R G = 0 {\displaystyle R_{G}=0} ).
Обычно в качестве индикатора используется гальванометр.
- Сопротивление R 2 {\displaystyle R_{2}} второй ветви изменяют до тех пор, пока показания гальванометра не станут равны нулю, то есть потенциалы точек узлов D и B не станут равны. По отклонению стрелки гальванометра в ту или иную сторону можно судить о направлении протекания тока на диагонали моста BD (см. рисунок) и указывают в какую сторону изменять регулируемое сопротивление R 2 {\displaystyle R_{2}} для достижения «баланса моста».
Когда гальванометр показывает ноль, говорят, что наступило «равновесие моста» или «мост сбалансирован». При этом:
- отношение R 2 / R 1 {\displaystyle R_{2}/R_{1}} равно отношению R x / R 3 {\displaystyle R_{x}/R_{3}} :
R 2 R 1 = R x R 3 , {\displaystyle {\frac {R_{2}}{R_{1}}}={\frac {R_{x}}{R_{3}}},}
откуда
R x = R 2 R 3 R 1 ; {\displaystyle R_{x}={\frac {R_{2}R_{3}}{R_{1}}};}
- разность потенциалов между точками B и D (см. рисунок) равна нулю;
- ток по участку BD (через гальванометр) (см. рисунок) не протекает (равен нулю).
Сопротивления R 1 {\displaystyle R_{1}} , R 3 {\displaystyle R_{3}} должны быть известны заранее.
- Изменяют сопротивление R 2 {\displaystyle R_{2}} до баланса моста.
- Вычисляют искомое сопротивление R x {\displaystyle R_{x}} :
R x = R 2 R 3 R 1 . {\displaystyle R_{x}={\frac {R_{2}R_{3}}{R_{1}}}.}
Вывод формулы см. ниже.
Точность
При плавном изменении сопротивления R 2 {\displaystyle R_{2}} гальванометр способен зафиксировать момент наступления равновесия с большой точностью. Если величины R 1 {\displaystyle R_{1}} , R 2 {\displaystyle R_{2}} и R 3 {\displaystyle R_{3}} были измерены с малой погрешностью, величина R x {\displaystyle R_{x}} будет вычислена с большой точностью.
В процессе измерения сопротивление R x {\displaystyle R_{x}} не должно изменяться, так как даже небольшие его изменения приведут к нарушению баланса моста.
Недостатки
К недостаткам предложенного способа можно отнести:
- необходимость регулирования сопротивления R 2 {\displaystyle R_{2}} . На поиски «равновесия» тратится время. Гораздо быстрее измерить несколько параметров цепи и вычислить R x {\displaystyle R_{x}} по другой формуле.
Принцип работы моста Уитстона
Мостовая схема Ч. Уинстона состоит из 2-х плеч. В каждом 2 резистора. Соединяет 2 параллельные ветви еще одна. Ее название – мостик. Ток проходит от клеммы с минусом к верхнему пику мостовой схемы.
Разделившись по 2 параллельным ветвям, ток идёт к положительной клемме. Величина сопротивления в каждой ветви непосредственно влияет на количество тока. Равное сопротивление на обеих ветвях говорит о том, что в них течет аналогичное количество тока. В таких условиях мостовой элемент уравновешен.
Если в ветвях неравное сопротивление, ток в электросхеме начинает движение от ветви с высоким уровнем сопротивления к ветви с наименьшим. Так продолжается, пока 2 верхних элемента цепей остаются равны по своей величине. Аналогичное положение резисторы имеют в схемах, которые используют в системах контроля и измерения.
Условие баланса моста
Выведем формулу для расчёта сопротивления R x {\displaystyle R_{x}} .
Схема к расчёту сопротивления R x {\displaystyle R_{x}} . Красными стрелками показаны выбранные произвольно направления токов. Обозначения:
- I G {\displaystyle I_{G}} — ток, протекающий через гальванометр, ;
- I 1 {\displaystyle I_{1}} , I 2 {\displaystyle I_{2}} , I 3 {\displaystyle I_{3}} , I x {\displaystyle I_{x}} — токи, протекающие через элементы R 1 {\displaystyle R_{1}} , R 2 {\displaystyle R_{2}} , R 3 {\displaystyle R_{3}} и R x {\displaystyle R_{x}} соответственно, ;
- другие обозначения см. выше.
Первый способ
Считается, что сопротивление гальванометра R G {\displaystyle R_{G}} мало настолько, что им можно пренебречь ( R G = 0 {\displaystyle R_{G}=0} ). То есть, можно вообразить, что точки B и D соединены (см. рисунок).
Воспользуемся правилами (законами) Кирхгофа. Выберем:
- направления токов — см. рисунок;
- направления обхода замкнутых контуров — по часовой стрелке.
По первому правилу Кирхгофа сумма токов, входящих в точку (узел) равна нулю:
- для точки (узла) B:
I 3 + I G − I x = 0 ; {\displaystyle I_{3}\ +I_{G}\ -I_{x}\ =\ 0;}
- для точки (узла) D:
I 1 − I 2 − I G = 0. {\displaystyle I_{1}\ -I_{2}\ -I_{G}\ =\ 0.}
По второму правилу Кирхгофа сумма напряжений в ветвях замкнутого контура равна сумме ЭДС в ветвях этого контура:
- для контура ABD:
( R 3 ⋅ I 3 ) − ( R G ⋅ I G ) − ( R 1 ⋅ I 1 ) = 0 ; {\displaystyle (R_{3}\cdot I_{3})\ -(R_{G}\cdot I_{G})\ -(R_{1}\cdot I_{1})=0;}
- для контура BCD:
( R x ⋅ I x ) − ( R 2 ⋅ I 2 ) + ( R G ⋅ I G ) = 0. {\displaystyle (R_{x}\cdot I_{x})\ -(R_{2}\cdot I_{2})\ +(R_{G}\cdot I_{G})=0.}
Запишем 4‑е последних уравнения для «сбалансированного моста» (то есть учтём, что I G = 0 {\displaystyle I_{G}=0} ):
{ I 3 = I x I 1 = I 2 R 3 ⋅ I 3 = R 1 ⋅ I 1 R x ⋅ I x = R 2 ⋅ I 2 {\displaystyle {\begin{cases}I_{3}=I_{x}\\I_{1}=I_{2}\\R_{3}\cdot I_{3}=R_{1}\cdot I_{1}\\R_{x}\cdot I_{x}=R_{2}\cdot I_{2}\end{cases}}}
Поделив 4‑е уравнение на 3‑е, получим:
R x ⋅ I x R 3 ⋅ I 3 = R 2 ⋅ I 2 R 1 ⋅ I 1 . {\displaystyle {\frac {R_{x}\cdot I_{x}}{R_{3}\cdot I_{3}}}={\frac {R_{2}\cdot I_{2}}{R_{1}\cdot I_{1}}}.}
Выразив R x {\displaystyle R_{x}} , получим:
R x = R 2 ⋅ I 2 ⋅ R 3 ⋅ I 3 I 1 ⋅ R 1 ⋅ I x . {\displaystyle R_{x}={\frac {R_{2}\cdot I_{2}\cdot R_{3}\cdot I_{3}}{I_{1}\cdot R_{1}\cdot I_{x}}}.}
С учётом того, что
{ I 3 = I x I 1 = I 2 {\displaystyle {\begin{cases}I_{3}=I_{x}\\I_{1}=I_{2}\end{cases}}}
получим
R x = R 2 ⋅ R 3 R 1 . {\displaystyle R_{x}={\frac {R_{2}\cdot R_{3}}{R_{1}}}.} Второй способ
Считается, что сопротивление гальванометра R G {\displaystyle R_{G}} велико настолько, что точки B и D можно считать не соединёнными (см. рисунок) ( R G = ∞ {\displaystyle R_{G}=\infty } ).
Введём обозначения:
- φ A {\displaystyle \varphi _{A}} , φ B {\displaystyle \varphi _{B}} , φ C {\displaystyle \varphi _{C}} и φ D {\displaystyle \varphi _{D}} — соответственно потенциалы точек A, B, C и D, ;
- U A C {\displaystyle U_{AC}} — напряжение между точками C и A, :
U A C = φ A − φ C ; {\displaystyle U_{AC}=\varphi _{A}-\varphi _{C};}
- U D B {\displaystyle U_{DB}} — напряжение между точками D и B, :
U D B = φ D − φ B ; {\displaystyle U_{DB}=\varphi _{D}-\varphi _{B};}
- R A D C {\displaystyle R_{ADC}} — сопротивление участка ADC (последовательное соединение), :
R A D C = R 1 + R 2 ; {\displaystyle R_{ADC}=R_{1}+R_{2};}
- R A B C {\displaystyle R_{ABC}} — сопротивление участка ABC (последовательное соединение), :
R A B C = R 3 + R x ; {\displaystyle R_{ABC}=R_{3}+R_{x};}
- I A D C {\displaystyle I_{ADC}} , I A B C {\displaystyle I_{ABC}} — токи, протекающие на участках ADC и ABC соответственно, .
По закону Ома токи I A D C {\displaystyle I_{ADC}} , I A B C {\displaystyle I_{ABC}} равны:
I A D C = U A C R A D C = U A C R 1 + R 2 ; {\displaystyle I_{ADC}={\frac {U_{AC}}{R_{ADC}}}={\frac {U_{AC}}{R_{1}+R_{2}}};} I A B C = U A C R A B C = U A C R 3 + R x . {\displaystyle I_{ABC}={\frac {U_{AC}}{R_{ABC}}}={\frac {U_{AC}}{R_{3}+R_{x}}}.}
По закону Ома падения напряжения на участках DC и BC равны:
U D C = I A D C ⋅ R 2 ; {\displaystyle U_{DC}=I_{ADC}\cdot R_{2};} U B C = I A B C ⋅ R x . {\displaystyle U_{BC}=I_{ABC}\cdot R_{x}.}
Потенциалы в точках D и B равны:
φ D = φ C + U D C = φ C + I A D C ⋅ R 2 ; {\displaystyle \varphi _{D}=\varphi _{C}+U_{DC}=\varphi _{C}+I_{ADC}\cdot R_{2};} φ B = φ C + U B C = φ C + I A B C ⋅ R x . {\displaystyle \varphi _{B}=\varphi _{C}+U_{BC}=\varphi _{C}+I_{ABC}\cdot R_{x}.}
Напряжение между точками D и B равно:
U D B = φ D − φ B = ( φ C + I A D C ⋅ R 2 ) − ( φ C + I A B C ⋅ R x ) = I A D C ⋅ R 2 − I A B C ⋅ R x . {\displaystyle U_{DB}=\varphi _{D}-\varphi _{B}=\left(\varphi _{C}+I_{ADC}\cdot R_{2}\right)\ -\left(\varphi _{C}+I_{ABC}\cdot R_{x}\right)\ =I_{ADC}\cdot R_{2}-I_{ABC}\cdot R_{x}.}
Подставив выражения для токов I A D C {\displaystyle I_{ADC}} и I A B C {\displaystyle I_{ABC}} , получим:
U D B = U A C R 1 + R 2 ⋅ R 2 − U A C R 3 + R x ⋅ R x . {\displaystyle U_{DB}={\frac {U_{AC}}{R_{1}+R_{2}}}\cdot R_{2}-{\frac {U_{AC}}{R_{3}+R_{x}}}\cdot R_{x}.}
Учитывая, что для «сбалансированного моста» U D B = 0 {\displaystyle U_{DB}=0} , получим:
0 = U A C R 1 + R 2 ⋅ R 2 − U A C R 3 + R x ⋅ R x . {\displaystyle 0={\frac {U_{AC}}{R_{1}+R_{2}}}\cdot R_{2}-{\frac {U_{AC}}{R_{3}+R_{x}}}\cdot R_{x}.}
Поместив слагаемые по разные стороны от знака равенства, получим:
U A C R 1 + R 2 ⋅ R 2 = U A C R 3 + R x ⋅ R x . {\displaystyle {\frac {U_{AC}}{R_{1}+R_{2}}}\cdot R_{2}={\frac {U_{AC}}{R_{3}+R_{x}}}\cdot R_{x}.}
Сократив U A C {\displaystyle U_{AC}} , получим:
R 2 R 1 + R 2 = R x R 3 + R x . {\displaystyle {\frac {R_{2}}{R_{1}+R_{2}}}={\frac {R_{x}}{R_{3}+R_{x}}}.}
Умножив на произведение знаменателей, получим:
R 2 ⋅ ( R 3 + R x ) = R x ⋅ ( R 1 + R 2 ) . {\displaystyle R_{2}\cdot (R_{3}+R_{x})=R_{x}\cdot (R_{1}+R_{2}).}
Раскрыв скобки, получим:
R 2 ⋅ R 3 + R 2 ⋅ R x = R x ⋅ R 1 + R x ⋅ R 2 . {\displaystyle R_{2}\cdot R_{3}+R_{2}\cdot R_{x}=R_{x}\cdot R_{1}+R_{x}\cdot R_{2}.}
После вычитания R x ⋅ R 2 {\displaystyle R_{x}\cdot R_{2}} получим:
R 2 ⋅ R 3 = R 1 ⋅ R x . {\displaystyle R_{2}\cdot R_{3}=R_{1}\cdot R_{x}.}
Выразив R x {\displaystyle R_{x}} , получим:
R x = R 2 ⋅ R 3 R 1 . {\displaystyle R_{x}={\frac {R_{2}\cdot R_{3}}{R_{1}}}.}
В данном случае мостовая схема рассматривалась, как комбинация двух делителей, а влияние гальванометра считалось пренебрежимо малым.
Схема мостового измерителя
Принципиальная схема реального мостового измерителя емкости и индуктивности, который вам предлагается сегодня сделать, показана на рисунке 4. Вы, наверное уже догадались, что этот прибор будет работать от низкочастотного генератора и лабораторного источника сигнала, которые мы с вами уже сделали ранее.
При помощи моста можно измерять емкости от десятков пФ до единиц мкФ и индуктивности от десятков мкГн до единиц мГн.
В качестве индикатора баланса используются обычные головные телефоны, например, от аудиоплейера, которые подключаются в гнездо Х5
Обратите внимание -общий вывод гнезда никуда не припаян, а к схеме подключены выводы стереоканалов наушников. Это позволяет увеличить сопротивление телефонов потому, что обе звуковые катушки так будут включены последовательно
На разъем Х2 подаются прямоугольные импульсы с выхода нашего генератора, при этом S4 генератора должен быть в противоположном, показанному на схеме положении (см. «РК-12-2004, стр.36-38).
Рис. 4. Принципиальная схема мостового измерителя емкости и индуктивности.
Транзисторный ключ на VT1 (рис.4) защищает выход микросхемы генератора от перегрузки, которая может возникнуть в процессе работы с мостом. Переключателями S1-S5 выбирают пределы измерения и то, что нужно измерять (индуктивность или емкость). При измерении индуктивности измеряемые катушки нужно подключать к клеммам Х3, а измеряя емкость — измеряемые конденсаторы подключать к Х4.
Если вернуться к схемам, приведенным на рисунках ЗА и ЗБ, то, конденсаторы С1, С2 и С3 (рис. 4) это конденсатор С1 (рис.З А), а измеряемый конденсатор — это С2 (рис.ЗА). Индуктивности L1 и L2 показанные на схеме на рисунке 4, — это индуктивность L2 в схеме на рисунке ЗБ, а измеряемая индуктивность — это L1 на рисунке З Б.
Органом измерения и, одновременно, индикатором результата измерения служит переменный резистор R1. Его рукоятка имеет стрелку, а вокруг нее нанесена на корпусе прибора шкапа (таким же способом как шкала настройки генератора НЧ).
На разъем Х1 подается напряжение от лабораторного источника питания. При измерении емкостей величина этого напряжения должна быть установлена 10-12V, а при измерении индуктивностей — 4-5V. Индуктивность и емкость можно отсчитывать по одной и той же шкале
Это важно, поскольку для градуировки измерителя емкости можно приобрети достаточное количество конденсаторов разных емкостей, а с приобретением такого же количества разных катушек могут возникнуть проблемы. Поэтому, градуировав прибор на измерение емкости можно им пользоваться и для измерения индуктивности
На генераторе установите частоту около 1000 Гц. С такой частотой в дальнейшем и будет работать мост. Конденсаторы С1, С2 и С3 нужно выбрать с наименьшей погрешностью емкости. Если есть такая возможность лучше их емкости предварительно проверить при помощи какого-то точного прибора, измеряющего емкости. В качестве L2 и L1 лучше использовать готовые дроссели (на 100 мкГн и на 1 мГн).
Прибор можно собрать в любом подходящем по размерам корпусе, например, в пластмассовой мыльнице. В качестве переключателей S1-S4 можно использовать такие же как в генераторе НЧ, но не три, а пять модулей или простые тумблеры. Можно всех их заменить одним поворотным переключателем на пять положений.
Работая с прибором нужно помнить, что только один из S1-S5 может быть замкнутым, при этом все остальные разомкнуты.Шкала одна и та же для всех пределов и видов измерения. Поэтому, её можно отградуировать на одном пределе, например, «х0,01 мкФ». В этом случае, подготовьте эталонные конденсаторы, например, на 1000 пф, 1500 пф, 3000 пФ, 5000 пф, 7500 пФ, 0,01 мкФ, 0,015 мкФ, 0,02 мкФ, 0,05 мкФ, 0,1 мкФ.
Проводя контрольные измерения этих эталонных конденсаторов, при замкнутом S2, делайте на шкале метки : 1000 пФ -«0,1″, 1500пФ — ”0,15″, 3000 пФ — ”0,3», 5000 пФ — «0,5», 7500 пФ — «0,75», 0,01 мкФ — «1», 0,015 мкФ — «1,5», 0,02 мкФ — «2», 0,05 мкФ -«5», 0,1 мкФ — «10».
Метку нужно делать в том месте шкалы, при повороте рукоятки переменного резистора в которое, при подключенном эталонном конденсаторе, звук в наушниках пропадает.
Рк2005, 1.
Общее сопротивление без выполнения условия баланса
В случае, если условие баланса не выполнено, расчёт общего сопротивления довольно громоздкий.
Пользуясь правилами Кирхгофа, получаем систему уравнений:
{ I Σ = I 1 + I 4 = I 2 + I 3 I 5 = I 1 − I 2 = I 4 − I 3 R Σ ⋅ I Σ = R 1 ⋅ I 1 + R 2 ⋅ I 2 = R 3 ⋅ I 3 + R 4 ⋅ I 4 R 5 ⋅ I 5 = R 4 ⋅ I 4 − R 1 ⋅ I 1 = R 2 ⋅ I 2 − R 3 ⋅ I 3 {\displaystyle {\begin{cases}I_{\Sigma }=I_{1}+I_{4}=I_{2}+I_{3}\\I_{5}=I_{1}-I_{2}=I_{4}-I_{3}\\R_{\Sigma }\cdot I_{\Sigma }=R_{1}\cdot I_{1}+R_{2}\cdot I_{2}=R_{3}\cdot I_{3}+R_{4}\cdot I_{4}\\R_{5}\cdot I_{5}=R_{4}\cdot I_{4}-R_{1}\cdot I_{1}=R_{2}\cdot I_{2}-R_{3}\cdot I_{3}\end{cases}}}
Тогда после исключения из системы всех токов получим окончательный результат, представленный в наиболее кратком виде:
R Σ = ∑ 1 = i < j < k 5 R i R j R k − R 5 ( R 1 R 4 + R 2 R 3 ) ∑ 1 = i < j 5 R i R j − ( R 1 R 2 + R 3 R 4 ) , {\displaystyle R_{\Sigma }={\frac {\sum _{1=i
где в суммах в числителе и в знаменателе суммируются все возможные комбинации из произведений сопротивлений без повторений сомножителей (всего таких комбинаций по десять).
Схемы подключения
На практике для измерения сопротивления с помощью мостовых схем применяют двухпроводное и четырёхпроводное подключение.
Двухпроводная
схема подключения применяется при измерениях сопротивлений величиной выше 10 . К точкам B и C (см. рисунок) подключаются по одному проводу.
Четырёхпроводная
схема подключения применяется при измерении сопротивления величиной до 10 . К точкам B и C (см. рисунок) подключаются по два провода. Это позволяет исключить влияние сопротивления проводов на величину измеренного сопротивления R x {\displaystyle R_{x}} .
Где используют измерительный мост Уитстона?
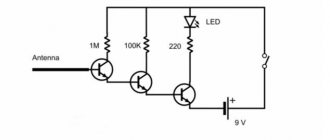
Самодельный драйвер для светодиодов от сети 220в
Измерительные элементы применяют в работе с кабельными линиями из металла. Они позволяют нейтрализовать постороннее влияние для более эффективной локализации дефектов. Гарантированы высокоточные результаты в рамках диапазона измеряемых величин.
С помощью мостовой схемы Уитстона можно вычислить сопротивление изменяющегося элемента. Схемы используют в конструкциях электронных весов, электронных термометров и терморезисторов.
Среди промышленных образцов широко известны приборы с ручной калибровкой равновесия:
- ММВ – измеряет сопротивление проводника постоянного напряжения;
- Р333 – схема одинарного моста, с помощью которой выявляется поврежденный участок кабеля.
История создания
В 1833 году Самуэль Хантер Кристи (англ. Samuel Hunter Christie) предложил схему, позже получившую название «мост Уитстона».
В 1843 году схема была усовершенствована Чарльзом Уитстоном (англ. Charles Wheatstone)[2] и стала называться «мостом Уитстона».
В 1861 году лорд Кельвин использовал мост Уитстона для измерения малых сопротивлений.
В 1865 году Максвелл с помощью изменённого моста Уитстона измерял силу переменного тока.
В 1926 году Алан Блюмлейн усовершенствовал мост Уитстона и запатентовал. Новое устройство стали называть в честь изобретателя.
Полупроводниковые схемы
Любой выпрямитель — это схема. Она включает в себя вторичную обмотку трансформатора, выпрямляющий элемент, электрический фильтр и нагрузку. При этом существует возможность получать умножение напряжения. Выпрямленное напряжение — это сумма постоянного и переменного напряжений. Переменная составляющая — это нежелательная компонента, которую уменьшают тем или иным способом. Но поскольку используются полуволны переменного напряжения, иначе быть не может.
Его можно уменьшить двумя способами:
- улучшая эффективность электрического фильтра;
- улучшая параметры выпрямляемого переменного напряжения.
Простейший выпрямитель однополупериодный. Он отсекает одну из полуволн переменного напряжения. Поэтому коэффициент пульсаций в такой схеме получается самым большим. Но если выпрямляется трехфазное напряжение с одним диодом в каждой фазе, а также одним и тем же фильтром, получится в три раза меньший коэффициент пульсаций. Однако наилучшими характеристиками обладают двухполупериодные выпрямители.
Использовать обе полуволны переменного напряжения можно двумя способами:
- по схеме моста;
- по схеме со средней точкой обмотки (схема Миткевича).
Сравним обе эти схемы для одного и того же значения выпрямленного напряжения. В схеме моста используется меньше витков вторичной обмотки трансформатора, что является преимуществом. Но при этом в однофазном выпрямительном мосте необходимы четыре диода. В схеме со средней точкой необходимо в два раза больше витков вторичной обмотки со средней точкой, что является недостатком. Еще один недостаток этой схемы — необходимость симметрии частей обмотки относительно средней точки.
Схема устройства стабилизатора напряжения
Асимметрия будет дополнительным источником пульсаций. Но зато в этой схеме нужны только два диода, что является преимуществом. При выпрямлении на диоде существует напряжение. Его величина почти не изменяется в зависимости от силы тока, протекающего через этот диод. Поэтому мощность, рассеиваемая на полупроводниковом диоде, растет по мере увеличения силы выпрямленного тока.
Это весьма ощутимо при большой силе тока, и поэтому полупроводниковые диоды размещаются на охлаждающих радиаторах и при необходимости обдуваются.
При выпрямлении тока большой силы два диода схемы со средней точкой будут экономичнее и компактнее в сравнении с четырьмя диодами выпрямительного моста. Схемы выпрямителей в свое время не появились из ниоткуда. Их изобрели инженеры. Поэтому схемы выпрямителей в литературе иногда называются в связи с именами своих первооткрывателей. Мостовая схема именуется как «полный мост Гретца». Схема со средней точкой — «выпрямитель Миткевича».
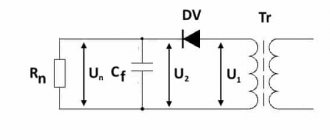
Силовой трансформатор
Это устройство предназначено для согласования напряжений на входе и выходе выпрямительного устройства. Другими словами, трансформатор осуществляет разделение сети нагрузки и сети питания. Существуют всевозможные варианты схем соединения обмоток этого трансформатора, выбор которых зависит от типа схемы выпрямления устройством. На величину выходного напряжения трансформатора U2 влияет величина напряжения на выходе выпрямительного моста Uн.
Трансформатор способен выполнить гальваническую развязку частоты f1 с сетью питания U1, I1, и нагрузочную цепь с Uн, Iн одновременно. В настоящее время появилась возможность проектировать и производить инверторы высокого напряжения, функционирующие на повышенной частоте и выпрямляющие напряжение. Для этого применяются схемы бестрансформаторного выпрямления, в которых блок вентилей подключается сразу к первичной сети питания.
Силовой трансформатор
Диодный мост
Этот блок выполняет основную функцию в устройстве выпрямителя, преобразуя переменный ток в постоянный. В блоке применяются чаще всего элементы в виде диодов. На выходе блока вентилей снимается постоянное напряжение, имеющее повышенный уровень импульсов, который зависит от числа фаз сети питания и схемой выпрямителя.
Диодный мост
Устройство фильтрования
Фильтрующая часть выпрямителя обеспечивает необходимый уровень пульсаций напряжения на выходе выпрямителя в соответствии с предъявляемыми требованиями нагрузки. В схеме фильтрующего устройства применяются сглаживающий дроссель или сопротивление, подключенные последовательно, и конденсаторы, подключенные параллельно выходу питания.
Однако чаще всего фильтры выполняют по схемам несколько сложнее. В маломощных выпрямителях нет необходимости в применении дросселя и резистора. В схемах выпрямителей для трехфазной сети величина импульсов меньше, тем самым становятся легче условия функционирования фильтра.
Классификация
В промышленности широко применяются уравновешенные и неуравновешенные измерительные мосты.
Работа уравновешенных
мостов (наиболее точных) основана на «нулевом методе».
С помощью неуравновешенных
мостов (менее точных) измеряемую величину определяют по показаниям измерительного прибора.
Измерительные мосты подразделяются на неавтоматические и автоматические.
В неавтоматических
мостах балансирование производится вручную (оператором).
В автоматических
балансировка моста происходит с помощью сервопривода по величине и знаку напряжения между точками D и B (см. рисунок).
Схемы измерительных мостов
Измерительные мосты переменного тока делят на 2 группы: двойные и одинарные. Одинарные имеют 4 плеча. В них 3 ветви создают цепь с 4 точками подключения.
В диагонали моста есть электромагнитный гальванометр, показывающий равновесие. В другой диагонали моста действует источник постоянного питания. Измерения могут происходить с погрешностями, которые зависят от их диапазона. По мере роста сопротивления чувствительность прибора уменьшается.
Двойной мост называют шестиплечим. Его плечи – измеряемое сопротивление (Rx), резистор (Ro) и 2 пары дополнительных резисторов (Rl, R2, R3, R4).
Применение для измерения неэлектрических величин
Мост Уитстона часто используется для измерения самых разнообразных неэлектрических параметров, например:
- механических деформаций упругих элементов в тензометрии;
- температуры;
- освещённости;
- состава вещества, в том числе влажности и газовом анализе;
- теплопроводности и теплоёмкости и многого другого.
Принцип действия всех этих приборов основан на измерении сопротивления чувствительного резистивного элемента-датчика, сопротивление которого изменяется при изменении воздействующей на него неэлектрической величины. Резистивный датчик (датчики) включается электрически в одно или несколько плеч моста Уитстона и измерение неэлектрической величины сводится к измерению изменения сопротивления датчиков.
Применение моста Уитстона в этих приложениях обусловлено тем, что позволяет измерять относительно малое изменение сопротивления, то есть в случаях когда Δ R x / R x ≪ 1. {\displaystyle \Delta R_{x}/R_{x}\ll 1.}
Обычно в современных измерительных приборах мост Уитстона подключается через аналого-цифровой преобразователь к цифровому вычислительному устройству, например, к микроконтроллеру, обрабатывающему сигнал моста. При обработке, как правило, производится линеаризация, масштабирование с преобразованием в численное значение неэлектрической величины в единицы её измерения, коррекция систематических погрешностей датчиков и измерительной схемы, индикация в удобном и наглядном для пользователя цифровом и/или машинно-графическом виде. Также может производиться статистическая обработка измерений, гармонический анализ и другие виды обработки.
Принцип работы тензометрических измерителей
Основная статья: Тензометрия
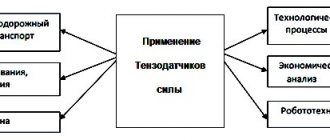
Тензодатчики тензорезисторы применяются в:
- электронных весах;
- динамометрах
- измерителях давления (манометрах);
- измерителях крутящего момента на валах (торсиометрах);
- измерителях деформации деталей под воздействием механической нагрузки и др.
При этом тензорезисторы, наклеенные на упругие деформируемые детали включаются в плечи моста, а полезным сигналом является напряжение диагонали моста между точками D
и
B
(см. рисунок).
Если выполняется соотношение:
R 1 / R 2 = R 3 / R x , {\displaystyle R_{1}/R_{2}=R_{3}/R_{x},}
то независимо от напряжения на диагонали моста между точками A
и
C
(напряжения) между точками
D
и
B
( U D B {\displaystyle U_{DB}} )) будет равно нулю:
U D B = 0. {\displaystyle U_{DB}=0.}
Но если R 1 / R 2 ≠ R 3 / R x , {\displaystyle R_{1}/R_{2}\neq R_{3}/R_{x},} то на диагонали появится ненулевое напряжение («разбаланс» моста), однозначно связанное с изменением сопротивления тензорезистора, и, соответственно, с величиной деформации упругого элемента, при измерении разбаланса моста измеряют деформацию, а так как деформация связана, например, в случае весов, с весом взвешиваемого тела, то и в результате измеряют его вес.
Для измерения знакопеременных деформаций помимо тензодатчиков часто используют пьезоэлектрические датчики. Последние в этих приложениях вытеснили тензодатчики благодаря лучшим техническим и эксплуатационным характеристикам. Недостатком пьезодатчиков является непригодность их для измерения медленных или статических деформаций.
Измерения других неэлектрических величин
Описанный принцип измерения деформации с помощью тензорезисторов в тензометрии сохраняется для измерения иных неэлектрических величин с применением других резистивных датчиков, сопротивление которых изменяется под воздействием неэлектрической величины.
Измерение температуры
В этих приложениях применяются резистивные датчики, находящиеся в тепловом равновесии с изучаемым телом, сопротивление датчиков изменяется при изменении их температуры. Также применяются датчики не контактирующие непосредственно с изучаемым телом, а измеряющие интенсивность теплового излучения от объекта, например, болометрические пирометры.
В качестве термочувствительных датчиков обычно используются резисторы, изготовленные из металлов — термометры сопротивления, имеющие положительный температурный коэффициент сопротивления, или полупроводниковые — терморезисторы с отрицательным температурным коэффициентом сопротивления.
Косвенно через измерение температуры также производится измерение теплопроводности, теплоёмкости, скорости потоков газов и жидкостей в термоанемометрах и измерение иных неэлектрических величин, связанных с температурой, например, концентрации компонента в газовой смеси с помощью термокаталитических датчиков и датчиков теплопроводности в газовой хроматографии.
Измерение потоков излучения
В фотометрах применяются датчики, изменяющие своё сопротивление в зависимости от освещенности — фоторезисторы. Также существуют резистивные датчики для измерения потоков ионизирующих излучений.
Для измерения электрического сопротивления имеется два варианта использования моста Уитстона:
- Определение абсолютного значения сопротивления путем сравнения с известным сопротивлением.
- Определение относительных изменений сопротивления.
Последний вариант используется в отношении тензометрических методов измерения. Он позволяет с большой точностью определить относительные изменения сопротивления тензодатчика в распространённом диапазоне от 10 -4 до 10 -2 Ом / Ом.
На изображении ниже показаны две разные иллюстрации моста Уитстона: на рисунке а) обычное изображение ромба, в котором используется мост Уитстона; на рисунке b) располагается изображение все той же электрической схемы, но более понятное для новичка.
Четыре ветви мостовой схемы образованы сопротивлениями от R 1 до R 4 . Угловые точки 2 и 3 обозначают соединения для напряжения возбуждения моста V s . Выходное напряжение моста V 0 , то есть сигнал измерения, доступно в угловых точках 1 и 4.
Общепринятого правила обозначения компонентов моста и соединений не существует. В популярной литературе есть всевозможные обозначения, и это отражено в уравнениях моста. Поэтому важно, чтобы обозначения и индексы, используемые в уравнениях, учитывались вместе с их положением в мостовых схемах, это поможет избежать путаницы.
Если напряжение питания V s приложено к точкам питания моста 2 и 3, то напряжение питания делится на две половины моста R 1 , R 2 и R 4 , R 3 как отношение соответствующих сопротивлений моста. , т. е. каждая половина моста образует делитель напряжения.
Мост может быть разбалансирован из-за разницы напряжений и электрических сопротивлений на R 1 , R 2 и R 3 , R 4 . Это можно рассчитать следующим образом:
если мост уравновешен и
где выходное напряжение моста V 0 равно нулю.
При заданной деформации сопротивление тензодатчика изменяется на величину ΔR. Это дает нам следующее уравнение:
Для измерения деформации сопротивления R 1 и R 2 в мосте Уитстона должны быть одинаковыми. То же самое относится к R 3 и R 4 .
С помощью нескольких упрощений можно вывести следующее уравнение:
На последнем этапе расчета ΔR / R необходимо заменить следующим:
Здесь k — коэффициент k тензодатчика, ε — деформация. Получаем следующее:
Уравнения предполагают, что все сопротивления в мосту изменяются. Обозначения, такие как: четверть моста, полумост, двойная четверть или диагональный мост и полный мост, являются обычными.
Хотя для обозначения таких схем используются вышеупомянутые определения типа: «полумост» или «четверть моста», на самом деле они не совсем корректны. Фактически, цепь, используемая для измерения, всегда является полной и полностью или частично формируется тензометрическими датчиками. Затем они дополняются постоянными резисторами, которые встроены в измерительные приборы.
Весовые терминалы обычно соответствуют очень строгим требованиям к точности. Поэтому, в отличие от экспериментальных измерительных приборов, весовые преобразователи всегда должны иметь полную мостовую схему с активными тензодатчиками на всех четырех плечах.
В случае, если необходимо устранить различные помехи и факторы препятствующие измерению, полномостовые или полумостовые схемы используются для анализа нагрузки. Важным условием является четкое различение напряжений и сил, таких как сжатие или растяжение, а также изгибающие, сдвиговые или скручивающие силы.
В таблице ниже показана зависимость положения тензометрических датчиков, типа используемой мостовой схемы и результирующего коэффициента моста B для нормальных сил, изгибающих моментов, крутящего момента и температуры. В небольших таблицах, приведенных для каждого примера, указан коэффициент моста B для каждого типа влияющей величины. Эти уравнения используются для вычисления эффективного напряжения от выходного сигнала моста V O / V S .
| Конфигурация моста | Вычисление | Измерение | Описание | Преимущества и недостатки | |
| 1 | Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки | Простой четвертьмост Простая четвертьмостовая схема с одним активным тензодатчиком | + Простая установка — Нормальная деформация и деформация изгиба накладываются друг на друга — Температурные эффекты не компенсируются автоматически | ||
| 2 | Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки | Квартальный мост Две четвертьмостовые схемы, одна активно измеряет деформацию, другая монтируется на пассивном компоненте, изготовленном из того же материала, который не подвергается деформации. | + Температурные эффекты хорошо компенсируются — Нормальную деформацию и деформацию изгиба нельзя разделить (наложение изгиба) | ||
| 3 | Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки | Полумост Пуассона Два активных тензодатчика, соединенных полумостом, один из которых расположен под углом 90 ° к другому | + Температурные эффекты хорошо компенсируются, когда материал изотропный | ||
| 4 | Измерение деформации изгибаемой балки | Полумост На противоположных сторонах конструкции установлены два тензодатчика. | + Температурные эффекты хорошо компенсируются + Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) | ||
| 5 | Измерение деформации на стержне растяжения / сжатия | Диагональный мост На противоположных сторонах конструкции установлены два тензодатчика. | + Нормальная деформация измеряется независимо от деформации изгиба (изгиб исключен) | ||
| 6 | Измерение деформации на стержне растяжения / сжатия Измерение деформации изгибаемой балки | Полный мост 4 тензодатчика установлены с одной стороны конструкции как полноценный мост. | + Температурные эффекты хорошо компенсируются + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) — Нормальную деформацию и деформацию изгиба нельзя разделить (наложение изгиба) | ||
| 7 | Измерение деформации на стержне растяжения / сжатия | Диагональный мост Два активных тензодатчика, два пассивных тензодатчика | + Нормальная деформация измеряется независимо от деформации изгиба (изгиб исключен) + Температурные эффекты хорошо компенсируются | ||
| 8 | Измерение деформации изгибаемой балки | Полный мост Четыре активных тензодатчика соединены как полный мост | + Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются | ||
| 9 | Измерение деформации на стержне растяжения / сжатия | Полный мост Четыре активных тензодатчика, два из которых повернуты на 90 ° | + Нормальная деформация измеряется независимо от деформации изгиба (изгиб исключен) + Температурные эффекты хорошо компенсируются + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) | ||
| 10 | Измерение деформации изгибаемой балки | Полный мост Четыре активных тензодатчика, два из которых повернуты на 90 ° | + Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются | ||
| 11 | Измерение деформации изгибаемой балки | Полный мост Четыре активных тензодатчика, два из которых повернуты на 90 ° | + Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются | ||
| 12 | Измерение деформации изгибаемой балки | Полный мост Четыре активных тензодатчика, соединенные как полный мост | + Разделение нормальной и изгибающей деформации (измеряется только изгибающий эффект) + Температурные эффекты хорошо компенсируются + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) | ||
| 13 | Измерение деформации скручивания | Полный мост Установлены четыре тензодатчика, каждый под углом 45 ° к главной оси, как показано. | + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются | ||
| 14 | Измерение деформации скручивания при ограниченном пространстве для установки | Полный мост Четыре тензодатчика устанавливаются как полный мост под углом 45 ° и накладываются друг на друга (розетки) | + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются | ||
| 15 | Измерение деформации скручивания при ограниченном пространстве для установки | Полный мост Четыре тензодатчика устанавливаются как полный мост под углом 45 ° и накладываются друг на друга (розетки) | + Высокий выходной сигнал и отличное подавление синфазных помех (CMR) + Температурные эффекты хорошо компенсируются | ||
В примерах 13, 14 и 15 для измерения крутящего момента предполагается цилиндрический вал. По причинам, связанным с симметрией, допускается изгиб в направлении X и Y. Такие же условия действуют и для стержней с квадратным или прямоугольным поперечным сечением.
Пояснения к символам:
| Т | Температура |
| F n | Нормальная сила |
| М б | Изгибающий момент |
| M bx , M — пользователем | Изгибающий момент для направлений X и Y |
| М д | Крутящий момент |
| ε s | Видимое напряжение |
| ε n | Нормальное напряжение |
| ε б | Деформация изгиба |
| ε d | Деформация скручивания |
| ε | Эффективная деформация в точке измерения |
| ν | Коэффициент Пуассона |
| Активный тензодатчик | |
| Тензодатчик для температурной компенсации | |
| Резисторный или пассивный тензодатчик |
Модификации
Используя мост Уитстона, можно с большой точностью измерять сопротивление.
Различные модификации моста Уитстона позволяют измерять другие физические величины:
- ёмкость;
- индуктивность;
- импеданс;
- концентрацию газов;
- и другое.
Прибор explosimeter (англ.) позволяет определить, превышена ли допустимая концентрация горючих газов в воздухе.
Мост Кельвина (англ. Kelvin bridge), также известный как мост Томсона (англ. Thomson bridge), позволяет измерять малые сопротивления, изобретён Томсоном.
Вид спереди прибора, построенного на основе моста Кельвина
Прибор Максвелла позволяет измерять силу переменного тока, изобретён Максвеллом в 1865 году, усовершенствован Блюмлейном около 1926 года.
Мост Максвелла (англ. Maxwell bridge) позволяет измерять индуктивность.
Мост Фостера (англ. Carey Foster bridge) позволяет измерять малые сопротивления, описан Фостером (англ. Carey Foster) в документе, опубликованном в 1872 году.
Делитель напряжения Кельвина-Варли (англ. Kelvin–Varley divider) построен на основе моста Уитстона.