Сглаживающие фильтры выпрямителей блоков питания.
Потолковали мы основательно на предыдущей странице про разные виды диодных выпрямителей, перебросились парой фраз на тему простейших ёмкостных фильтров, а вопрос достижения параметра коэффициента пульсаций
Кп в пределах 10-5… 10-4 так и повис в воздухе — уж очень немалым получается номинал ёмкости сглаживающего конденсатора.
Коэффициент пульсаций выпрямленного напряжения Кп является важнейшим параметром выпрямителя. Его численное значение равно отношению амплитудного значения пульсирующего напряжения к его постоянной составляющей. Напомню выдержку из печатного издания, приведённую на предыдущей странице:
«Коэффициент пульсаций выбирают самостоятельно в зависимости от предполагаемой нагрузки, допускающей питание постоянным током вполне определённой «чистоты»: 10-3… 10-2 (0,1-1%) — малогабаритные транзисторные радиоприёмники и магнитофоны, 10-4… 10-3 (0,01-0,1%) — усилители радио и промежуточной частоты, 10-5… 10-4 (0,001-0,01%) — предварительные каскады усилителей звуковой частоты и микрофонных усилителей.»
Помимо этого в характеристиках выпрямителей может использоваться и понятие коэффициента фильтрации (коэффициента сглаживания). Коэффициент фильтрации, он же коэффициент сглаживания — величина, численно равная отношению коэффициента пульсаций на входе фильтра к коэффициенту пульсаций на выходе фильтра Кс = Кп-вх/Кп-вых . Для многозвенных фильтров коэффициент фильтрации равен произведению коэффициентов фильтрации отдельных звеньев.
В слаботочных цепях вопрос снижения пульсаций решается легко и кардинально — применением интегральных стабилизаторов. Параметр подавления пульсаций (Ripple Rejection) у подобных массовых ИМС составляет не менее 50дБ (в 360раз по напряжению), что при высокой «чистоте» выходного напряжения позволяет уменьшить ёмкости электролитов в 5-10 раз.
Если же у разработчика нет возможности (либо желания) включать в состав устройства стабилизаторы напряжения, то реальным подспорьем окажутся индуктивно-ёмкостные или активные сглаживающие фильтры.
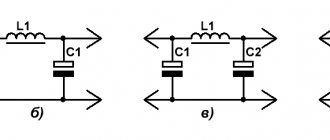
Начнём с фильтров, выполненных из индуктивных элементов – дросселей и из ёмкостных элементов – конденсаторов. Рис.1
На Рис.1а приведена схема простейшего ёмкостного сглаживающего фильтра. Принцип действия заключается в накоплении электрической энергии конденсатором фильтра и последующей отдачи этой энергии в нагрузку.
Для того чтобы не ограничиваться 50-ти герцовыми блоками питания, но и иметь возможность расчёта фильтров импульсных ИП, приведу универсальные формулы, учитывающие частоту входного сигнала F: С1 = Iн/(3,14×Uн×F×Кп) для однополупериодных выпрямителей и С1 = Iн/(6,28×Uн×F×Кп) — для двухполупериодных. Кп — это коэффициент пульсаций, равный отношению амплитудного значения пульсирующего напряжения к его постоянной составляющей, а F — частота переменного напряжения на входе диодного выпрямителя.
Переходим к индуктивно-ёмкостным LC фильтрам. ВНИМАНИЕ!!! Потребность в такого рода цепях возникает исключительно в случаях необходимости получить низкий уровень пульсаций в достаточно мощных сетевых блоках питания, либо в высокочастотных импульсных ИП. Связано это с тем, что для эффективной работы LC-фильтра, индуктивное сопротивление катушки XL на частоте подавления стремятся сделать значительно больше Rн. А это, в свою очередь, приводит к тому, что в условиях низких частот и малых токов (высоких Rн) индуктивность дросселя получается необоснованно высокой.
Г-образный индуктивно-ёмкостной LC фильтр 2-го порядка (Рис.1б) обладает значительно лучшими фильтрующими свойствами по сравнению с обычным ёмкостным. Произведение LC (Гн*мкФ) зависит от необходимого коэффициента сглаживания фильтра и определяется по приближенной формуле: L1(Гн)×С1(МкФ) = 25000/(F2(Гц)×Кп) для однополупериодных выпрямителей и L1×С1 = 12500/(F2×Кп) — для двухполупериодных, где С1(МкФ)/L1(мГн) = 1000/Rн2(Ом).
Схема П-образного LC-фильтра приведена на Рис.1в. Сглаживающее действие П-образного LC-фильтра можно упрощённо представить как совместное действие двух фильтров, описанных выше, а коэффициент сглаживания — как произведение коэффициентов сглаживания звеньев: ёмкостного и Г-образного индуктивно-ёмкостного. Наилучшими фильтрующими свойствами обладают LC-фильтры Чебышева. Напишем формулу, исходя из рекомендаций, изложенных на странице ссылка на страницу: С1 = С2 ; С1(МкФ)/L1(мГн) = 1176/Rн2(Ом).
Уменьшить напряжение пульсаций на выходе однозвенного П-образного LC-фильтра можно, включив параллельно дросселю L1 неполярный конденсатор С3 (Рис.1г), который вместе с индуктивностью катушки образует режекторный фильтр. Если ёмкость конденсатора С3 выбрать такой, чтобы резонансная частота контура L1-С3 равнялась частоте пульсаций (F при однополупериодном выпрямлении или 2F при двухполупериодном), то большая часть напряжения пульсаций задержится этим контуром и лишь незначительная перейдёт в нагрузку. Итак: С3 = 1/(39,44×L1×F2) для однополупериодных выпрямителей и С3 = 1/(9,86×L1×F2) — для двухполупериодных. Все остальные номиналы элементов — такие же, как в предыдущей схеме.
Давайте сдобрим пройденный материал онлайн таблицей.
КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ СЛАЖИВАЮЩЕГО ФИЛЬТРА БЛОКА ПИТАНИЯ.
Транзисторные фильтры по сравнению с ёмкостными сглаживающими фильтрами имеют меньшие габариты, массу и более высокий коэффициент сглаживания пульсаций. Они позволяют уменьшить в десяток раз (при том же уровне пульсаций) номинал сглаживающего конденсатора, либо уменьшить в аналогичное количество раз амплитуду пульсаций при неизменном значении ёмкости.
Рис.2
На Рис.2а представлена схема наиболее распространённого транзисторного фильтра.
Напряжение с высокой амплитудой пульсаций, поступающее на коллектор транзистора, по сути, является напряжением питания эмиттерного повторителя, образованного Т1. В это же самое время цепь базы питается через резисторы смещения и интегрирующую цепь R1C1, которая сглаживает пульсации напряжения на базе. Чем больше постоянная времени T=R1C1, тем меньше пульсации напряжения на базе, а так как устройство представляет собой эмиттерный повторитель, то на выходе фильтра пульсации будут столь же малыми, как и на базе. Для того, чтобы снизить зависимость напряжения на выходе фильтра от уровня передаваемой мощности, ток через делитель R1R2 выбирают в 5…10 раз большим, чем ток, ответвляющийся в базу при минимальном сопротивлении нагрузки. При расчёте номиналов элементов делителя, следует исходить из напряжения на базе транзистора: Uб = Uвх — Uвх пульсаций — (2,5…3В) . В этом случае будет обеспечена работа регулирующего транзистора в активном режиме, а падение напряжения на нём составит величину: Uкэ = Uвх пульсаций + (3,1…3,6В) . Коэффициент полезного действия транзисторного фильтра будет тем больше, чем меньше падание постоянного напряжения на силовом транзисторе. Из формулы видно, что для обеспечения высокого КПД активного сглаживающего фильтра, на вход устройства следует подавать уже отфильтрованное до определённого уровня напряжение. На практике это делается включением на вход простейшего ёмкостного фильтра (Рис.1а), уровень пульсаций которого можно посчитать на приведённом выше калькуляторе.
Эффективность активных сглаживающих фильтров напрямую зависит от величины коэффициента усиления транзистора. Чем выше h21 полупроводника, тем больших величин можно выбрать номиналы резисторов R1, R2 — тем лучшими фильтрующими свойствами будет обладать схема. Поэтому в данной ситуации не стоит даже рассматривать транзисторы с h21
Для дальнейшего улучшения фильтрующих свойств сглаживающего фильтра можно применить двухзвенный RC-фильтр в цепи базы транзистора (Рис.2б). Здесь сумма значений сопротивления резисторов R1 и R2 равна сопротивлению резистора R1 в предыдущем устройстве, а сопротивление резистора R3 равно сопротивлению резистора R2 в фильтре (Рис.2а).
Ещё эффективней будет работать транзисторный фильтр, у которого в цепь базы транзистора вместо R2 (Рис.1а), либо R3 (Рис.1б) включить стабилитрон с напряжением пробоя, равным значению, рассчитанному для резистивного делителя.
Выпрямители: Однофазный однополупериодный выпрямитель
Рис. 3.4-1. Однофазный однополупериодный выпрямитель (а) и временные диаграммы, поясняющие его работу (б)
На интервале времени \(\left[ {0;} T/2 \right]\) полупроводниковый диод выпрямителя смещен в прямом направлении и напряжение, а следовательно, и ток в нагрузочном резисторе повторяют форму входного сигнала. На интервале \(\left[ T/2 {;} T \right]\) диод смещен в обратном направлении и напряжение (ток) на нагрузке равно нулю. Таким образом, среднее значение напряжения на нагрузочном резисторе будет равно:
\(U_{н ср} = \cfrac{1}{T} {\huge \int \normalsize}_{0}^{T} U_н \operatorname{d}t = \cfrac{1}{T} {\huge \int \normalsize}_{0}^{T/2} U_{вх max} \sin{\left( \omega t \right)} \operatorname{d}t = \)
\(= — \cfrac{U_{вх max}}{T \omega} \cos{\left( \omega t \right)}{\huge \vert \normalsize}_{0}^{T/2} \approx \cfrac{U_{вх max}}{\pi} = \sqrt{2} \cfrac{U_{вх д}}{\pi}\),
где \(U_{вх д}\) — действующее значение переменного напряжения на входе выпрямителя.
Аналогично, для среднего тока нагрузки:
\(I_{н ср} = \cfrac{1}{2 \pi} {\huge \int \normalsize}_{0}^{\pi} I_{max} \sin{\left( \omega t \right)} \operatorname{d} t \approx \cfrac{I_{max}}{\pi} = {0,318} \cdot I_{max} \),
где \(I_{max}\) — максимальная амплитуда выпрямленного тока.
Действующее значение тока нагрузки \(I_{н д}\) (через диод протекает такой же ток):
\(I_{н д} = \sqrt{\cfrac{I_{max}^2}{2 \pi} {\huge \int \normalsize}_{0}^{\pi^{ }} \sin{\left( \omega t \right)}^2 \operatorname{d} t} = \cfrac{I_{max}}{2} = {0,5} \cdot I_{max} \)
Отношение среднего значения выпрямленного напряжения \(U_{н ср}\) к действующему значению входного переменного напряжения \(U_{вх д}\) называется коэффициентом выпрямления (\(K_{вып}\)). Для рассматриваемой схемы \(K_{вып} = {0,45}\).
Максимальное обратное напряжение на диоде \(U_{обр max} = U_{вх max} = \pi U_{н ср}\) , т.е. более чем в три раза превышает среднее выпрямленное напряжение (это следует учитывать при выборе диода для выпрямителя).
Спектральный состав выпрямленного напряжения имеет вид (разложение в ряд Фурье):
\(U_н = \cfrac{1}{\pi} U_{вх max} + \cfrac{1}{2} U_{вх max} \sin{\left( \omega t \right)} — \cfrac{2}{3 \pi} \cos{\left( 2 \omega t \right)} — \)
\( — \cfrac{2}{15 \pi} U_{вх max} \cos{\left( 4 \omega t \right)} — {…} \)
Коэффициент пульсаций, равный отношению амплитуды низшей (основной) гармоники пульсаций к среднему значению выпрямленного напряжения, для описываемой схемы однополупериодного выпрямителя равен:
\(K_п = \cfrac{U_{пульс max 01}}{U_{н ср}} = \cfrac{\pi}{2} = {1,57}\).
Как видно, однополупериодное выпрямление имеет низкую эффективность из-за высокой пульсации выпрямленного напряжения.
Еще один отрицательный аспект однополупериодного выпрямления связан с неэффективным использованием силового трансформатора, с которого берется переменное напряжение. Это обусловлено тем, что в токе вторичной обмотки трансформатора существует постоянная составляющая, равная среднему значению выпрямленного тока. Такая составляющая не трансформируется, т.е.:
\(I_1 \cdot w_1 = \left( I_2 – I_{н ср} \right) w_2\) ,
где \(I_1\), \(I_2\) — токи первичной и вторичной обмоток, а \(w_1\), \(w_2\) — число витков первичной и вторичной обмоток трансформатора.
Временнáя диаграмма тока первичной обмотки трансформатора (рис. 3.4-2) подобна диаграмме тока вторичной обмотки, но смещена на величину \(I_{н ср} \cfrac{w_2}{w_1}\).
Рис. 3.4-2. Временная диаграмма токов в первичной и вторичной обмотках силового трансформатора, нагруженного на схему однофазного однополупериодного выпрямителя
В сердечнике трансформатора за счет постоянной составляющей тока вторичной обмотки создается постоянный магнитный поток \(\Phi_0 = w_2 \cdot I_0\). Это явление принято называть вынужденным намагничиванием сердечника трансформатора. Оно может вызвать насыщение магнитной системы трансформатора, т.е. увеличение тока холостого хода, действующего значения первичного тока и следовательно, расчетной мощности первичной обмотки трансформатора, что обусловливает увеличение необходимых размеров трансформатора в целом.
Дополнительный минус однополупериодного выпрямления состоит в наличии участка стабильного тока, что также снижает эффективность использования трансформатора по мощности. Максимальный коэффициент использования трансформатора по мощности для такой схемы не превышает \(k_{тр P} \approx {0,48}\).
Для снижения уровня пульсаций на выходе выпрямителя включаются разнообразные индуктивно-емкостные фильтры. Наличие конденсаторов и индуктивностей в цепи нагрузки оказывает значительное влияние на работу выпрямителя.
В маломощных выпрямителях обычно применяют простейший емкостный фильтр, который представляет собой конденсатор, включенный параллельно нагрузке (рис. 3.4-3).
Рис. 3.4-3. Схема однофазного однополупериодного выпрямителя с емкостным фильтром (а) и временные диаграммы, поясняющие его работу (б)
В установившемся режиме работы, когда напряжение на входе выпрямителя \(U_{вх}\) больше напряжения на нагрузке \(U_н\) и диод выпрямителя открыт, конденсатор будет подзаряжаться, накапливая энергию, поступающую от внешнего источника. Когда же напряжение на входе выпрямителя упадет ниже уровня открывания диода и он закроется, конденсатор начнет разряжаться через \(R_н\), предотвращая при этом быстрое падение уровня напряжения на нагрузке. Таким образом, результирующее напряжение на выходе выпрямителя (на нагрузке) окажется уже не таким пульсирующим, а будет значительно сглажено, причем тем сильнее, чем большую емкость будет иметь применяемый конденсатор.
Обычно, емкость конденсатора фильтра выбирают такой, чтобы его реактивное сопротивление было намного меньше сопротивления нагрузки (\(1/ \omega C \ll R_н\)). В этом случае пульсации напряжения на нагрузке малы и допустимо предполагать, что это напряжение постоянно (\(U_н \approx {const}\)). Примем: \(U_н = U_{вх max} \cos{\beta}\), где \(\beta\) — некоторая константа, определяющая значение напряжения на нагрузке. Очевидно, что в общем случае \(\beta\) зависит от емкости конденсатора, сопротивления нагрузки, частоты входного напряжения и т.п. Физический смысл этой величины можно понять из временных диаграмм, приведенных на рис. 3.4-4. Как видно, \(\beta\) отражает длительность временного интервала в одном периоде колебаний внешнего напряжения, когда диод выпрямителя находится в открытом состоянии (\(\beta = \omega \cdot t_{откр}/2\)). Угол \( \beta\) принято называть углом отсечки.
Рис. 3.4-4. График зависимости \(A(\beta)\)
Для тока, протекающего через диод в открытом состоянии, можно записать:
\( I_д = \cfrac{U_{вх} — U_н}{r} \) ,
где \(r\) — активное сопротивление, обусловленное сопротивлением диода в открытом состоянии и сопротивлением вторичной обмотки трансформатора (иногда его называют сопротивлением фазы выпрямителя).
Учитывая, что \(U_{вх} = U_{вх max} \sin{\left( \omega t \right)} \):
\(I_д = \cfrac{U_{вх max}}{r} \left( \sin{\left( \omega t \right)} — \cos{\left( \beta \right)} \right) = \cfrac{U_{вх max}}{r} \left(\sin{\left(\varphi \right)} — \cos{\left( \beta \right)} \right)\) (3.4.1)
Среднее за период значение выпрямленного тока диода (учитывая, что диод открыт только на участке \(\varphi = \left[\pi/2 – \beta ; \pi/2 + \beta \right]\):
\(I_{д ср} =\cfrac{1}{2 \pi} {\huge \int \normalsize}_{\frac{\pi}{2} — \beta}^{\frac{\pi}{2} + \beta} \cfrac{U_{вх max}}{r} \left( \sin{ \left( \varphi \right)} — \cos{\left( \beta \right)} \right) \operatorname{d} \varphi =\)
\(= \cfrac{U_{вх max}}{\pi r} \left( \sin{\left( \beta \right)} — \beta \cos{\left( \beta \right)} \right) \)
Поскольку \(U_{вх max} = \cfrac{U_н}{\cos{\left( \beta \right)}} \):
\(I_{д ср} =\cfrac{U_н}{\pi r} \cdot \cfrac{\sin{\left( \beta \right)} — \beta \cos{\left( \beta \right)}}{\cos{\left( \beta \right)} } = \cfrac{U_н}{\pi r} A \left( \beta \right) \),
где \( A \left( \beta \right) = \cfrac{\sin{\left( \beta \right)} — \beta \cos{\left( \beta \right)}}{\cos{\left( \beta \right)}} = \operatorname{tg} \left( \beta \right) — \beta \) (3.4.2)
Формула (3.4.2) очень важна при расчете выпрямителя. Ведь угол отсечки \(\beta\) не является заранее известным исходным параметром, как правило, его приходится вычислять на основании заданных выходного напряжения (\(U_н\)), сопротивления (\(R_н\)) или тока нагрузки (\(I_н\)), а также параметров применяемого диода и трансформатора (которые определяют сопротивление фазы \(r\)). Располагая этими данными и учитывая (3.4.2) можно определить значение коэффициента \(A\):
\(A \left( \beta \right) = \cfrac{I_{д ср} \pi r}{U_н} \)
Средний ток через диод \(I_{д ср}\) равен среднему току нагрузки \(I_{н ср}\), а учитывая, что напряжение на нагрузке предполагается неизменным, то и мгновенное значение тока через нагрузку равно току диода: \(I_н = I_{д ср}\). Таким образом:
\(A \left( \beta \right) = \cfrac{I_{н} \pi r}{U_н} = \cfrac{\pi r}{R_н} \)
Для нахождения угла отсечки \(\beta\) при известном коэффициенте \(A(\beta)\) на практике обычно пользуются графиком (рис. 3.4-4).
Максимальное значение тока диода достигается при \(U_{вх} = U_{вх max}\) в момент времени, когда \(\varphi = \pi/2 \), т.е. согласно выражения (3.4.1):
\( I_{д max} = \cfrac{U_{вх max}}{r} \left( 1 — \cos{\left( \beta \right)} \right) = \cfrac{U_н}{r} \cdot \cfrac{\pi \left( 1 — \cos{\left( \beta \right)} \right)}{\cos{\left( \beta \right)}} \)
И далее, учитывая (3.4.2) получим:
\( I_{д max} = \cfrac{I_{д ср} \cdot \pi}{A \left( \beta \right)} \cdot \cfrac{1- \cos{\left( \beta \right)}}{\cos{\left( \beta \right)}}\), где \(F \left( \beta \right) = \cfrac{\pi \cdot \left( 1 — \cos{\left( \beta \right)} \right)}{\sin{\left( \beta \right)} — \beta \cos{\left( \beta \right)}}\)
График функции \(F(\beta)\) представлен на рис. 3.4-5. Из него видно, что с уменьшением угла отсечки \(\beta\) существенно увеличивается амплитуда тока через вентили.
Рис. 3.4-5. График зависимости \(F(\beta)\)
Таким образом, емкостный характер нагрузки выпрямителя приводит к тому, что выпрямительный диод оказывается открытым в течение меньшего промежутка времени, а амплитуда тока, проходящего в это время через диод, оказывается больше, чем в аналогичной схеме, работающей на чисто активную нагрузку. Этот факт необходимо учитывать при выборе диода, который должен выдерживать повторяющийся ток соответствующей амплитуды и более того, нормально переносить первоначальный всплеск тока при включении, когда происходит первоначальная зарядка конденсатора.
Указанная закономерность справедлива не только для описываемой схемы однофазного однополупериодного выпрямления. Аналогичным образом будет происходить работа и других рассматриваемых далее схем, имеющих нагрузку емкостного характера.
Требуемый коэффициент пульсаций на выходе однофазного однополупериодного выпрямителя с емкостным фильтром \(K_п\) может быть получен при правильном выборе емкости сглаживающего конденсатора. Для ее нахождения используется следующая формула:
\( С = \cfrac{H(\beta)}{r \cdot K_п}\),
где \(H(\beta)\) — это еще один вспомогательный коэффициент, значение которого находится по графику (рис. 3.4-6).
Рис. 3.4-6. График зависимости \(H(\beta)\)
Емкостный фильтр характерен для выпрямителей, рассчитанных на малые токи нагрузки. При больших токах обычно применяют индуктивные фильтры. Такой фильтр представляет собой катушку индуктивности (обычно с ферромагнитным сердечником), включенную последовательно с нагрузкой (рис. 3.4-7). Наличие индуктивности в цепи нагрузки также как и емкость оказывает значительное влияние на режим работы вентилей выпрямителя.
Рис. 3.4-7. Схема однофазного однополупериодного выпрямителя с индуктивным фильтром (а) и временные диаграммы, поясняющие его работу (б)
Работа схемы на рис. 3.4-7 описывается уравнением:
\( U_{вх max} \sin{\left( \omega t \right)} = L \cfrac{\operatorname{d} I_н}{\operatorname{d} t} + I_н R_н \)
Приняв ток в цепи в начальный момент времени \((t = 0)\) равным нулю, решив данное уравнение получим следующее выражение для тока в цепи нагрузки:
\(I_н(t) = \cfrac{U_{вх max}}{\sqrt{R_н^2 + {\left( \omega L \right)}^2}} \left( \sin{\left( \omega t — \theta \right)} + e^{- \cfrac{R_н t}{L}} \sin{( \theta )} \right) \),
где \( \theta = \operatorname{arctg} \left( \cfrac{\omega L}{R_н} \right) \)
Временная диаграмма, отражающая эту зависимость приведена на рис. 3.4-7(б). По ней хорошо виден физический смысл константы \(\theta\). Она представляет собой угол, на который запаздывает основной всплеск тока в нагрузке относительно инициирующего его всплеска напряжения на входе выпрямителя.
Если проанализировать зависимость тока нагрузки \(I_н(t)\), можно заметить, что его амплитуда с увеличением индуктивности катушки падает (соответственно падает и его среднее значение). Т.е. среднее значение напряжения на нагрузке оказывается меньшим, чем в случае отсутствия индуктивности, уменьшаются также пульсации выходного напряжения. Сами колебания тока оказываются сдвинутыми относительно колебаний входного напряжения на угол \(\theta\). Это является причиной скачкообразного приложения к диоду в момент его запирания отрицательного обратного напряжения величиною до \(U_{обр} = U_{вх max}\).
Описанный режим работы вентилей (затягивание тока, уменьшение его амплитуды, скачкообразное приложение обратного напряжения) при наличии индуктивного фильтра характерен для всех схем выпрямителей. Индуктивный фильтр обычно применяют в схемах мощных выпрямителей, поскольку в этом случае требуемая для существенного изменения параметров выходного напряжения индуктивность оказывается незначительной.
Наиболее эффективно сглаживание пульсаций выпрямленного напряжения осуществляется с помощью сложных многозвенных фильтров, в состав которых входят и катушки индуктивности и конденсаторы (основой таких фильтров являются т.н. Г- или П-образные звенья).
| Следующая > |
Пульсации выпрямленного напряжения
Рассмотренные схемы выпрямителей давали возможность получить на нагрузке выпрямленное, но пульсирующее напряжение. Недопустимо большие пульсации напряжения нарушают нормальный режим работы электронной аппаратуры создают фон на ее выходе, вызывают искажения сигналов, приводят к неустойчивости работы электронного устройства в целом. Поэтому для устранения пульсации выпрямленного напряжения
в схему выпрямителя на его выходе включают сглаживающие фильтры.
| Прежде чем познакомиться с практическими схемами фильтрации, рассмотрим физические процессы в схеме двухполупериодного выпрямителя для случая, когда последовательно с сопротивлением нагрузки включен дроссель L (рис. 117, а), т. е. когда выпрямитель нагружен на индуктивное и активное сопротивления. Напряжение URнL, приложенное к цепи Rн — L, имеет форму положительных синусоидальных полуволн; форма же тока, протекающего через нагрузку, отличается от формы выпрямленного напряжения. При увеличении напряжения URнL в индуктивности L возникает э. д. с. самоиндукции eL, которая противодействует увеличению тока. Она направлена навстречу возрастающему напряжению URнL и поэтому на графике показана с обратной полярностью. Рис. 117. Работа двухполупериодного выпрямителя: а —на индуктивность и активное сопротивление; б — на емкость и активное сопротивление. |
Как только ток первого вентиля В1 перестанет возрастать (достигает максимума), э. д. с. самоиндукции становится равной нулю. В следующую часть периода, когда полярность ее изменится, она будет препятствовать уменьшению тока в цепи Rн — L, поэтому ток прекращается не в момент а позже, в момент времени t’. В момент времени t’ открывается также вентиль В2 и ток в нагрузке складывается из возрастающего тока вентиля В2 и уменьшающегося тока вентиля В1, поддерживаемого э. д. с. самоиндукции (последний замыкается теперь через вентиль В2, так как вентиль В1 заперт).
Среднее значение выпрямленного тока уже незначительно отличается от максимального тока через вентиль, причем это отличие будет тем меньше, чем больше индуктивность L. Одновременно уменьшаются и пульсации выпрямленного напряжения
. Так, при ωL, — (5÷8) Rн пульсации напряжения на нагрузке не превышают 20%.
Обратное напряжение на вентиле равно сумме э. д. с. еII и напряжения на входе цепи Rн—L:
Uобр.макс2ЕmII≈πUcр.
В общем случае среднее значение выпрямленного напряжения на нагрузке равно
Uср = Uср.х.х — Iср (Ri + rII + rдр),
где Uср.х.х — напряжение на выходе выпрямителя при отключенной нагрузке в режиме холостого хода; Iср (Ri + rII + rдр) — напряжение потерь на актив-пых сопротивлениях элементов схемы.
Из последнего равенства следует, что с увеличением тока через нагрузку (при уменьшении Rн) увеличивается наклон внешней характеристики. Однако этот наклон не зависит от индуктивности дросселя, поэтому в выпрямителе с индуктивной нагрузкой целесообразно применять вентили с малым внутренним сопротивлением Ri (селеновые или ионные вентили).
На рис. 117, б приведены двухполупериодная схема выпрямителя, нагруженного на параллельно подключенные конденсатор С и сопротивление Rн, а также графики, поясняющие работу этой схемы.
Конденсатор дважды за каждый период подзаряжается до напряжения UC.макс поочередно через вентиль В1 и вентиль В2. Когда напряжение на соответствующей половине вторичной обмотки трансформатора становится выше напряжения UС на конденсаторе, он. подзаряжается в промежутки времени t1 — t2, t3 — t4 и разряжается на нагрузку в промежутки времени t2—t3, t4— t5. При этом ток в нагрузке поддерживается за счет энергии, накопленной в конденсаторе. Вентили в это время заперты. Чем больше сопротивление нагрузки, тем медленнее разряжается конденсатор, тем меньше изменяется (меньше пульсирует) напряжение на нагрузке.
Среднее значение выпрямленного напряжения примерно равно амплитуде напряжения на половине вторичной обмотки трансформатора: обратное напряжение в 2 раза больше (≈2ЕmII), коэффициент пульсации не превышает 15% при С≈8÷10 мкф.
Следует заметить, что ток в нагрузке протекает в течение всего полупериода, в то время как ток через вентиль проходит только лишь часть полупериода, причем максимальное значение этого тока в 3—4 раза больше среднего значения выпрямленного. Поэтому если необходимо получить от выпрямителя ток в 100 ма, то допустимый максимальный ток вентиля должен быть не менее 300 ма.
Наклон внешней характеристики зависит не только от величины внутреннего сопротивления вентиля и вторичной обмотки трансформатора, но и от постоянных времени заряда и разряда конденсатора:
tзар ≈ С(Ri+r’II); tразр = CRн
Величина выпрямленного напряжения резко зависит от величины тока нагрузки. При Rн = ∞, т. е., когда Iср = 0, напряжение на емкости максимально; при уменьшении Rн напряжение Uср падает.
Выпрямитель, работающий на емкость, можно рассматривать как источник с большим внутренним сопротивлением. В момент включения схемы имеет место бросок тока, происходит первоначальный заряд конденсатора С, ток в цепи ограничивается только внутренним сопротивлением вентилей, поэтому возникает опасность выхода одного из них из строя.
Коэффициент пульсации
| [Home] | [Donate!] [Контакты] |
Коэффициент пульсации
Коэффициент пульсации — отношение абсолютного уровня пульсации к постоянной составляющей сигнала. Иначе говоря, коэффициент пульсации — мера пульсации в относительных единицах. Несмотря на то что, казалось бы, можно дать довольно чёткое определение данному понятию, на самом деле оно крайне неоднозначное. Причина этого в том, что существуют совершенно разные подходы к определению абсолютного уровня пульсаций.
Оглавление Коэффициент пульсации Введение Определение коэффициента пульсации Определения понятия в соответствии с нормативной документацией Альтернативные определения Источники информации
Введение
Довольно часто, например, при измерении различных физических величин, при анализе качества электропитания устройств и при рассмотрении множества других вопросов, мы сталкиваемся с явлением пульсации — нежелательным периодическим отклонением величины (допустим, выходного напряжения блока питания) относительно среднего значения.
Мерой пульсации является уровень пульсации, который может быть выражен в абсолютных величинах (амплитуда пульсации, размах, действующее значение и т.д.). Но иногда бывает удобно рассматривать уровень пульсации не в абсолютном выражении, а в относительных единицах. Отношение величины, характеризующей уровень пульсаций к постоянной составляющей сигнала, называют коэффициентом пульсации.
Коэффициент пульсации можно использовать, например, как объективную характеристику качества выходного напряжения источника питания, которая позволяет сравнивать между собой разные устройства, без привязки к абсолютным значениям выходных напряжений. Коэффициент пульсации позволяет судить о применимости данного источника для питания той или иной нагрузки, ведь для обеспечения работоспособности потребителя, пульсация не должна превышать заданных для него допустимых пределов.
Другой простой пример, когда бывает полезным рассмотрение коэффициента пульсации — анализ выпрямителей. Так, для идеализированного выпрямителя без сглаживающего фильтра, коэффициент пульсации является параметром схемы, не зависящим ни от входного напряжения, ни от нагрузки и дающего возможность легко сопоставлять между собой разные типы выпрямителей.
Определение коэффициента пульсации
Некоторые сложности с использованием данного параметра возникают в связи с тем, что можно вводить в рассмотрение множество разных коэффициентов пульсации, в зависимости от того, какую величину выберем в качестве абсолютной меры уровня пульсаций. Поэтому важно уточнять, о каком именно коэффициенте идёт речь. Чем некоторые авторы порой пренебрегают и тогда остаётся только догадываться, что имелось в виду.
Можно выделить три основных подхода к определению коэффициента пульсации, которые чаще всего используются в литературе и отражены в нормативной документации (стандартах).
1. Коэффициент пульсации — отношение половины размаха пульсации к среднему значению величины (или, что то же самое, к постоянной составляющей величины). Под размахом пульсации понимается разность между максимальным и минимальным значением величины: $$ k=\frac {U_{max}-U_{min}} {2 U_0}. $$
Рис. %img:rpl_def
Для практического измерения коэффициента пульсации удобно воспользоваться осциллографом и определить величины Umin, Umax. Если для оценки постоянной составляющей воспользоваться приближением \(U_0 \approx (U_{min}+U_{max})/2,\) то получаем следующую формулу, удобную для практического определения коэффициента пульсации: $$ k \approx \frac {U_{max}-U_{min}} {U_{max}+U_{min}}. $$
Существует аналогичное определение, но в нём используется не половина размаха, а полный размах пульсаций.
2. Коэффициент пульсации — отношение размаха пульсации к среднему значению величины (к постоянной составляющей величины): $$ k=\frac {U_{max}-U_{min}} {U_0}, $$ или, в более удобной форме для вычисления по результатам измерений запишем как $$ k \approx 2 \; \frac {U_{max}-U_{min}} {U_{max}+U_{min}}. $$
Но можно использовать не только амплитудные значения величины пульсаций, а, например, действующее (среднеквадратичное) значение напряжения пульсации. Тогда получим следующее определение.
3. Коэффициент пульсации — отношение среднеквадратичного значения переменной составляющей к абсолютному значению постоянной составляющей изменяющейся величины: $$ k=\frac {U_{eff}} {U_0}. $$
Каждое из рассмотренных определений имеет свою область применения. Выбор определяется тем, какой из коэффициентов наилучшим образом отображает реальные характеристики пульсации в данном случае.
Коэффициенты, вычисляемые по амплитуде и размаху пульсации (первое и второе определения) в целом равноценны, лишь отличаются друг от друга в 2 раза. Они характеризуют наибольшее отклонение величины от среднего значения. Хорошо подходят, например, для оценки качества выходного напряжения источников питания. Как правило, питаемое устройство предъявляет вполне определённые требования к пиковым отклонениям питающего напряжения, что позволяет на основании амплитудного коэффициента пульсации сделать вывод о применимости источника по пульсациям.
В некоторых же случаях больший интерес представляет не амплитуда, а действующее значение пульсации, которое определяет мощность пульсации на резистивной нагрузке. И тогда отдают предпочтение третьему определению.
Действующее значение величины, а значит и вычисленный по ней коэффициент пульсации оказывается малочувствителен к единичным кратковременным выбросам величины («иголкам» сигнала), которым соответствует малая переносимая в нагрузку энергия и которые вносят малый вклад в среднюю мощность, рассеиваемую на нагрузке.
Иногда эта особенность коэффициента пульсации по действующему значению оказывается полезной.
Определения понятия в соответствии с нормативной документацией
Поскольку коэффициент пульсаций — очень важный технический параметр, его не обошли вниманием в стандартах.
Посмотрим, например, что по данному вопросу можно найти в стандартах достаточно авторитетной организации IEC (Международной электротехнической комиссии). Осуществляя деятельность по разработке стандартов, IEC также проделала огромную работу с целью унификации терминологии в области электротехники, результатом чего стало создание Международного электротехнического словаря (Electropedia), доступного on-line.
Воспользовавшись поиском по словарю, обнаруживаем, что термины «пульсация», «коэффициент пульсации» используются в разных предметных областях: математика; электромагнитная совместимость; силовая электроника и др. Это ещё одна из причин многозначности термина.
Если, например, обратиться к разделу электромагнитной совместимости, то обнаружим, что там рассматриваются два вида коэффициентов пульсации:
- peak-ripple factor (коэффициент пульсации по амплитудному значению, пиковый коэффициент пульсации) — отношение пикового значения переменной составляющей к абсолютному значению постоянной составляющей изменяющейся величины (перевод определения из документа IEC-60050-161; под пиковым значением понимается просто размах пульсации)*;
- r.m.s.-ripple factor (коэффициент пульсации по среднеквадратичному значению, среднеквадратичный коэффициент пульсаций) — отношение среднеквадратичного значения переменной составляющей к абсолютному значению постоянной составляющей изменяющейся величины (перевод определения из документа IEC-60050-161; среднеквадратичное значение — это то, что раньше было принято называть действующим значением).
* Вариант на английском: peak-ripple factor — the ratio of the peak-to-valley value of the ripple content to the absolute value of the direct component of a pulsating quantity. Значение термина «peak-to-valley value» также может быть найдено в Electropedia: peak-to-valley value, peak-to-peak value — difference between the global maximum value and the global minimum value in the same specified interval of the argument. Note 1 to entry: For a periodic quantity, the specified interval has a range equal to the period. Note 2 to entry: The synonym «peak-to-peak value» should be used only when the global maximum and minimum values are of different signs.
В разделе «Силовая электроника» обнаруживаем термин «DC ripple factor» (коэффициент пульсации постоянного тока), который определяется как отношение половины разницы между максимальным и минимальным значениями пульсирующего тока к среднему значению этого тока (ratio of half the difference between the maximum and minimum value of a pulsating direct current to the mean value of this current), смотрите IEC-60050-551. Это определение похоже на рассмотренное ранее определение для peak-ripple factor (коэффициент пульсации по амплитудному значению), но здесь для расчёта берётся не полный размах пульсации, а половина.
Наверно есть основания для введения двух однотипных определений, но избавиться от путаницы это совсем не помогает.
Найти упоминание о коэффициенте пульсации можно и в ГОСТ. Так, во многих статьях, касающихся темы пульсации, даётся ссылка на «ГОСТ 23875-88 Качество электрической энергии. Термины и определения», в котором приводится сразу несколько вариантов определения:
- Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей* пульсирующего напряжения (тока) к его постоянной составляющей. Примечание. Для целей стандартизации допускается относить к номинальному напряжению (току). * Не вполне очевидно, что понимается под «наибольшим значением переменной составляющей». Возможно, это амплитуда.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
Первые два определения имеют свои аналоги в IEC, а последнее — уже что-то новенькое. И опять же, не обошлось без доли таинственности. Так как среднее значение переменной составляющей равно 0, можно предположить, что в определении имелось в виду нечто иное. Скорее всего, это «среднее по модулю значение переменного напряжения (тока)», которое в этом же ГОСТе определяется как «среднее за период значение модулей мгновенных значений переменного напряжения (тока)». Вероятно, в каких-то случаях использовать этот коэффициент имеет смысл.
Рассмотрев так подробно вопрос о коэффициенте пульсации с точки зрения ГОСТ 23875-88, осталось только отметить, что этот ГОСТ с 2012 года утратил силу. Так что теперь ссылка на него выглядит как не слишком убедительное обоснование для использования того или иного определения*.
* Тем не менее, например, в действующем «ГОСТ 23414-84 Преобразователи электроэнергии полупроводниковые. Термины и определения (с Изменением N 1)» имеется ссылка на утративший силу ГОСТ 23875-88. Оказывается так можно.
Однако, тут нам на помощь приходят другие ГОСТы. Так, в «ГОСТ 26567-85 Преобразователи электроэнергии полупроводниковые. Методы испытаний» (на момент написания этой статьи имеет статус действующего), даётся наглядное объяснение «в картинках», рис. %img:h. На рисунке: 1 — огибающая мгновенных значений пульсирующего напряжения; t — время, в течение которого проводят наблюдения. Как видим, за величину пульсаций принимается половина размаха пульсаций. Также даётся расчётная формула (для вычисления коэффициента в процентах): $$ k_{пул}=\frac{U_{пул}}{U_{ном}}\cdot 100, $$ т.е. отношение половины размаха пульсации к номинальному значению величины.
Рис. %img:h
Данное определение в некоторой степени аналогично рассмотренному выше определению «DC ripple factor» (коэффициент пульсации постоянного тока) из IEC-60050-551.
Подобные определения можно найти и в других ГОСТах, например, в «ГОСТ Р 52907-2008 Источники электропитания радиоэлектронной аппаратуры. Термины и определения»: коэффициент пульсации постоянного выходного напряжения [тока] источника электропитания РЭА — величина, равная отношению наибольшего значения переменной составляющей пульсирующего постоянного выходного напряжения [тока] к его среднему значению в установившемся режиме работы источника электропитания радиоэлектронной аппаратуры.
Правда, данный стандарт является национальным (на что намекает символ Р в обозначении), но тем не менее.
Альтернативные определения
Справедливости ради нужно отметить, что рассмотренные выше определения коэффициента пульсации не являются единственно возможными и в литературе можно встретить другие варианты.
В принципе, под коэффициентом пульсации можно понимать отношение любой меры уровня пульсаций к среднему значению величины. Поэтому, в случае необходимости, можно вводить в рассмотрение самые экзотические варианты определения. Например, за уровень пульсаций можем принять сумму гармоник переменной составляющей с удобными нам весовыми коэффициентами.
В простейшем случае берём первую гармонику с коэффициентом 1 и получаем ещё один вариант определения, который достаточно часто можно встретить в отечественной литературе: коэффициент пульсации — отношение амплитуды первой гармоники (или низшей, или основной — в разных формулировках) к среднему значению напряжения (т.е., к постоянной составляющей).
Впрочем, известная доля популярности ещё не означает, что это определение является удачным. Во-первых, из рассмотрения исключаются все гармонические составляющие, кроме «основной», в то время как вклад «неосновных» может быть весьма значительным; в результате полученный коэффициент очень косвенно отражает реальное положение дел. Во-вторых, практическое измерение коэффициента не является простым — требуется выделение (фильтрация) одной гармоники для измерения её амплитуды.
Но если, например, имеем дело с питанием устройства, для которого нормируются вполне определённые компоненты в спектре пульсации, то описанный вариант определения вполне годится.
Источники информации
- IEC, International Electrotechnical Commission (Международная электротехническая комиссия).
- Electropedia (Международный электротехнический словарь).
- ГОСТ 26567-85 Преобразователи электроэнергии полупроводниковые. Методы испытаний
- ГОСТ Р 52907-2008 Источники электропитания радиоэлектронной аппаратуры. Термины и определения
- ГОСТ 23414-84 Преобразователи электроэнергии полупроводниковые. Термины и определения (с Изменением N 1)
- ГОСТ 23875-88 Качество электрической энергии. Термины и определения
author: hamper; date: 2019-12-01; updated: 2021-10-29
Определение и формула коэффициента пульсации
Коэффициент пульсации напряжения (Кп) – это величина, определяющая отношение максимальной составляющей переменного напряжения (Uпер.макс.) к его постоянной составляющей (Uпост). Для удобства она выражается в процентах.
Расчёт коэффициента пульсации по напряжению
Аналогично рассчитываются и пульсации тока.
Расчёт коэффициента пульсации по току
Iпер. макс. – это переменная составляющая тока. Iпост. – его постоянная составляющая.